Реклама

Наш канал:

Таненбаум Э.- Архитектура компьютера. стр.531

Другой пример — дистрибутивный закон:

ax(b-c) = axb-axc.

Подсчитаем обе части выражения для а = 5, й = 210ис = 195. В левой части 5 х 15 = 75. В правой части 75 не получается, поскольку результат выполнения операции ах b выходит за пределы ряда.

Исходя из этих примеров, кто-то может сделать вывод, что компьютеры совершенно непригодны для выполнения арифметических действий. Вывод, естественно, неверен, но эти примеры наглядно показывают, как важно понимать механизм работы компьютера и знать о его ограничениях.

Позиционные системы счисления

Обычное десятичное число состоит из цепочки десятичных разрядов и иногда десятичной точки (запятой). Общая форма записи показана на рис. А.1. Десятка выбрана в качестве основы возведения в степень (и называется основанием системы счисления), поскольку мы используем 10 цифр. В компьютерах удобнее иметь дело с другими основаниями системы счисления. Самые важные из них — 2, 8 и 16. Соответствующие системы счисления называются двоичной, восьмеричной и шестнадцатеричной.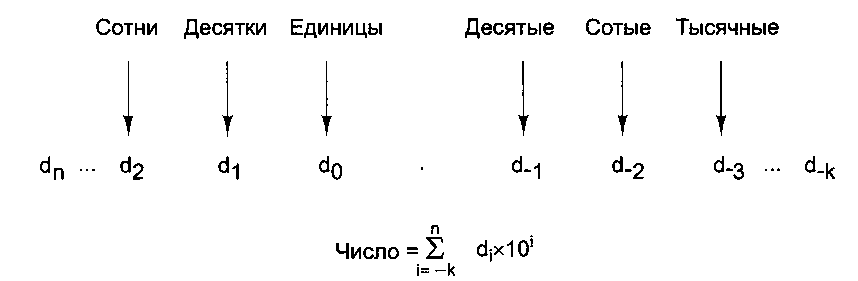

Рис. А.1. Общая форма десятичного числа

Система счисления с основанием k требует k различных символов для записи разрядов с 0 по k - 1. Десятичные числа строятся из 10 десятичных цифр:

0 123456789

Двоичные числа, напротив, строятся только из двух двоичных цифр:

0 1

Восьмеричные числа состоят из восьми цифр:

0 1234567

Для шестнадцатеричных чисел требуется 16 цифр. Это значит, что нам нужно 6 новых символов. Для обозначения цифр, следующих за девятью, принято использовать прописные латинские буквы от А до F. Таким образом, шестнадцате-ричные числа строятся из следующих цифр:

0 1 2 3 4 5 67 8 9 ABCDEF

Двоичный разряд (то есть 1 или 0) обычно называют битом. На рис. А.2 десятичное число 2001 представлено в двоичной, восьмеричной и шестнадцатеричной системах счисления. Число 7В9, очевидно, шестнадцатеричное, поскольку символ В встречается только в шестнадцатеричных числах. А число 111 может быть записано в любой из четырех систем счисления. Чтобы избежать двусмысленности, нужно использовать индекс для указания основания системы счисления.

В табл. А.1 ряд неотрицательных целых чисел представлен в каждой из четырех систем счисления.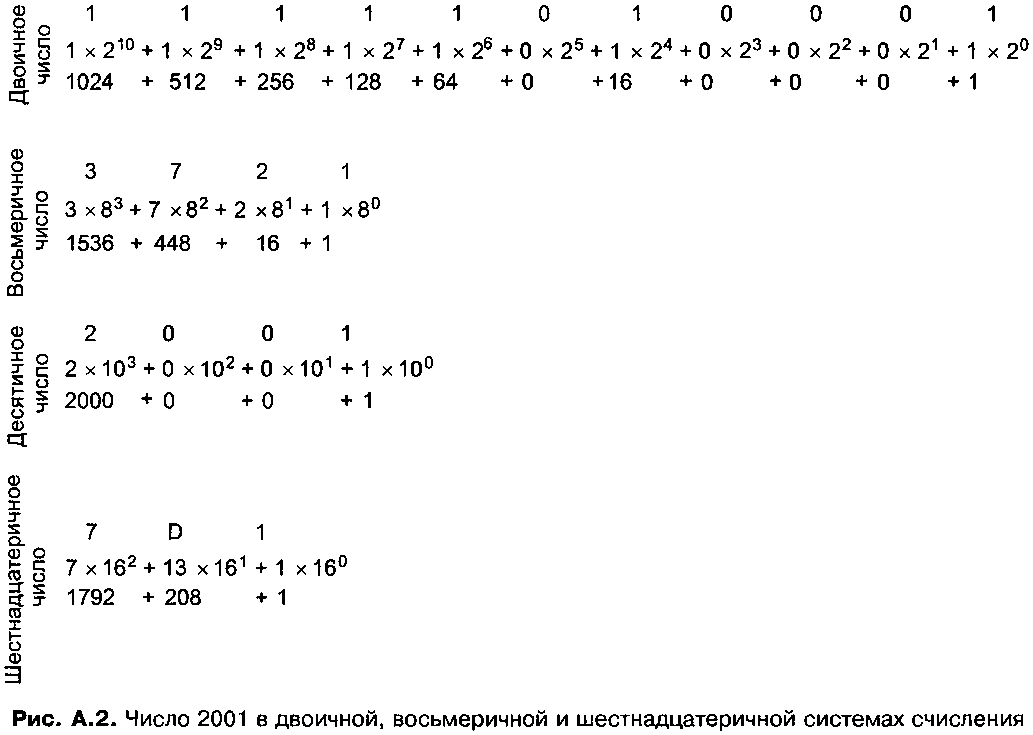

Таблица А.1. Десятичные числа и их двоичные, восьмеричные и шестнадцатеричные эквиваленты

Преобразование чисел из одной системы счисления в другую

Преобразовывать числа из восьмеричной в шестнадцатеричную или в двоичную систему счисления и обратно легко. Чтобы преобразовать двоичное число в восьмеричное, нужно разделить его на группы по три бита, причем три бита непосредственно слева от двоичной запятой формируют одну группу, следующие три бита слева от этой группы формируют вторую группу и т. д. Каждую группу по три бита можно преобразовать в один восьмеричный разряд со значением от 0 до 7 (см. первые строки таблицы А.1). Чтобы дополнить группу до трех битов, нужно спереди приписать один или два нуля. Преобразование из восьмеричной системы в двоичную тоже тривиально. Каждый восьмеричный разряд просто заменяется эквивалентным 3-разрядным числом. Преобразование из шестнадцате-ричной в двоичную систему по сути сходно с преобразованием из восьмеричной в двоичную систему, только каждый шестнадцатеричный разряд соответствует группе из четырех битов, а не из трех. На рис. А.З приведены примеры преобразований из одной системы в другую.