Стандарт IEEE 754 определяет три формата: с одинарной точностью (32 бита), с удвоенной точностью (64 бита) и с повышенной точностью (80 бит). Формат с повышенной точностью предназначен для уменьшения ошибки округления. Он применяется главным образом в арифметических устройствах с плавающей точкой, поэтому мы не будем о нем говорить. В форматах с одинарной и удвоенной точностью используются основание степени 2 для мантисс и смещенная экспонента. Форматы представлены на рис. Б.З.
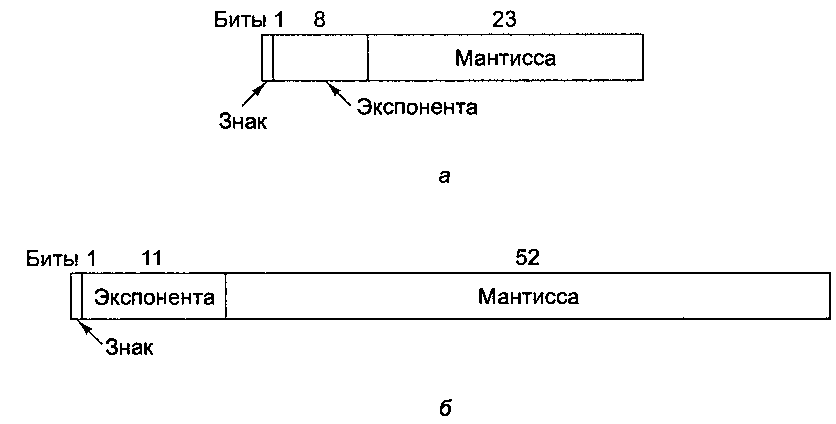
Рис. Б.З. Форматы стандарта IEEE с плавающей точкой: одинарная точность (а); удвоенная
точность (б)
Оба формата начинаются со знакового бита для всего числа; 0 указывает на положительное число, 1 — на отрицательное. Затем следует смещенная экспонента. Для формата одинарной точности смещение равно 127, а для формата удвоенной точности — 1023. Минимальная (0) и максимальная (255 и 2047)
экспоненты не используются для нормализованных чисел. У них есть специальное предназначение, о котором мы поговорим позже. В конце идут мантиссы по 23 и 52 бита соответственно.
Нормализованная мантисса начинается с двоичной точки, за которой следует 1 бит, а затем — остаток мантиссы. Следуя практике, начатой с компьютера PDP-11, компьютерщики осознали, что 1 бит перед мантиссой сохранять не нужно, а нужно просто считать, что он там есть. Следовательно, стандарт определяет мантиссу следующим образом. Она состоит из неявного бита, который всегда равен 1, и неявной двоичной точки, за которыми идут 23 или 52 произвольных бита. Если все 23 или 52 бита мантиссы равны 0, то мантисса имеет значение 1,0. Если все биты мантиссы равны 1, то числовое значение мантиссы немного меньше, чем 2,0. Во избежание путаницы в английском языке для обозначения комбинации из неявного бита, неявной двоичной точки и 23 или 52 явных битов вместо термина мантисса (mantissa) используется термин значащая часть числа (significand). Значащая часть числа (5) всех нормализованных чисел лежит в диапазоне 1 < s < 2.
Числовые характеристики стандарта IEEE для чисел с плавающей точкой даны в табл. Б.2. В качестве примеров рассмотрим числа 0,5, 1 и 1,5 в нормализованном формате с одинарной точностью. Они представлены шестнадцатеричны-ми числами 3F000000, 3F800000 и 3FC00000 соответственно.
Таблица Б.2. Характеристики чисел с плавающей точкой стандарта IEEE
|
Одинарная точность |
Удвоенная точность |
|
|
Количество битов в знаке |
||
|
Количество битов в экспоненте |
||
|
Количество битов в мантиссе |
||
|
Общее число битов |
||
|
Смещение экспоненты |
Смещение 127 |
Смещение 1023 |
|
Область значений экспоненты |
От-126 до+127 |
От-1022 до+1023 |
|
Самое маленькое нормализованное число |
2~126 |
2-1022 |
|
Самое большое нормализованное число |
Приблизительно 2128 |
Приблизительно 21024 |
|
Диапазон десятичных дробей |
Приблизительно от 10"38 до 1038 |
Приблизительно от Ю-308 до 10308 |
|
Самое маленькое ненормализованное число |
Приблизительно 1СГ45 |
Приблизительно 10~324 |
Традиционные проблемы, связанные с числами с плавающей точкой, — переполнение, потеря значимости и неинициализированные числа. Подход, используемый в стандарте IEEE, отчасти заимствован у машины CDC 6600. Помимо нормализованных чисел в стандарте предусмотрено еще 4 типа чисел (рис. Б.4).