Двоичная арифметика
Рисунок А.6 иллюстрирует сложение двоичных чисел.
Сложение двух двоичных чисел начинается с крайнего правого бита. Суммируются соответствующие биты в первом и втором слагаемых. Перенос совершается на одну позицию влево, как и в десятичной арифметике. В арифметике с дополнением до единицы бит переноса после сложения крайних левых битов
прибавляется к крайнему правому биту. Этот процесс называется циклическим переносом. В арифметике с дополнением до двух бит переноса, полученный в результате сложения крайних левых битов, просто отбрасывается. Примеры арифметических действий над двоичными числами показаны на рис. А.7.
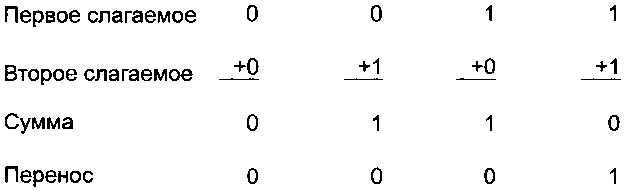
Рис. А.6. Таблица сложения для двоичных чисел
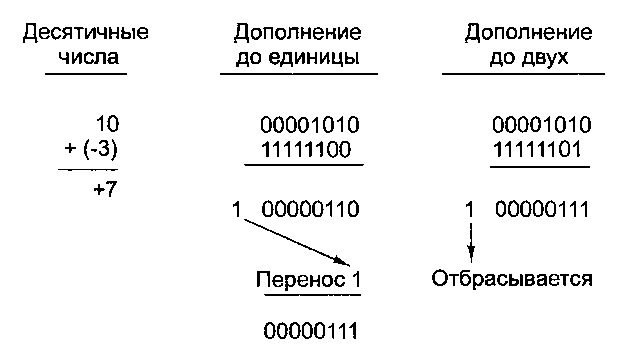
Рис. А.7. Сложение в системах с дополнением до единицы и с дополнением до двух
Если первое и второе слагаемые имеют противоположные знаки, ошибки переполнения не произойдет. Если они имеют одинаковые знаки, а результат — противоположный знак, значит, произошла ошибка переполнения и результат неверен. И в арифметике с дополнением до единицы, и в арифметике с дополнением до двух переполнение происходит тогда и только тогда, когда перенос в знаковый бит отличается от переноса из знакового бита. В большинстве компьютеров перенос из знакового бита сохраняется, но перенос в знаковый бит из результата не виден, поэтому обычно вводится специальный бит переполнения.
Вопросы и задания
1. Преобразуйте следующие числа в двоичные: 1984, 4000, 8192.
2. Преобразуйте двоичное число 1001101001 в десятичную, восьмеричную и ше-стнадцатеричную системы.
3. Какие из символьных строк BED, CAB, DEAD, DECADE, ACCEDED, BAG, DAD являются шестнадцатеричными числами?
4. Выразите десятичное число 100 в системах счисления с основаниями от 2 до 9.
5. Сколько различных положительных целых чисел можно выразить в k разрядах, использовав числа с основанием системы счисления г?
6. Большинство людей с помощью пальцев на руках могут сосчитать до 10. Однако компьютерщики способны на большее. Представим, что каждый палец соответствует одному двоичному разряду. Пусть вытянутый палец означает 1, а загнутый — 0. До скольки мы можем сосчитать, используя пальцы обеих рук? А если рассматривать пальцы на руках и на ногах? Представим, что большой палец левой ноги — это знаковый бит для чисел с дополнением до двух. Сколько чисел можно выразить таким способом?
7. Выполните следующие вычисления над 8-разрядными числами с дополнением до двух:
00101101 + 01101111 11111111 + 11111111 00000000 - 11111111 11110111 - 11110111
8. Выполните те же вычисления в системе с дополнением до единицы.
9. Далее приведены задания на сложение 3-разрядных двоичных чисел в системе с дополнением до двух. Для каждой суммы установите:
1) Равен ли знаковый бит результата единице.
2) Равны ли младшие три бита нулю.
3) Не произошло ли переполнения.
000 + 001 000 + 111 111 + ПО 100 + 111 100 + 100
10. Десятичные числа со знаком, состоящие из п разрядов, можно представить в п + 1 разрядах без знака. Положительные числа содержат 0 в крайнем левом разряде. Отрицательные числа получаются путем вычитания каждого разряда из 9. Например, отрицательным числом для 014 725 будет 985 274. Такие числа называются числами с дополнением до девяти. Они аналогичны двоичным числам с дополнением до единицы. Выразите следующие числа в виде 3-разрядных чисел в системе с дополнением до девяти: 6, -2, 100, -14, -1, 0.