1941 = 0,1941 х 104 = 1,941 х 103
Область значений определяется по числу разрядов в экспоненте, а точность — по числу разрядов в мантиссе. Существует несколько способов представления
того или иного числа, поэтому одна форма выбирается в качестве стандартной. Чтобы изучить свойства такого способа представления, рассмотрим представление с трехразрядной мантиссой со знаком в диапазоне 0,1 < |/| < 1 и двухразрядной экспонентой со знаком. Эти числа находятся в диапазоне от +0,100 х 10"" до +0,999 х 10+", то есть простираются почти на 199 значимых разрядов, хотя для записи числа требуется всего 5 разрядов и 2 знака.
Числа с плавающей точкой можно использовать для моделирования системы действительных чисел в математике, хотя здесь есть несколько существенных различий. На рис. Б.1 представлена ось действительных чисел. Она разбита на 7 областей:
1. Отрицательные числа меньше -0,999 х 10".
2. Отрицательные числа от -0,999 х 10" до -0,100 х 10"".
3. Отрицательные числа от -0,100 х 10"" до нуля.
4. Нуль.
5. Положительные числа от 0 до 0,100 х 10"".
6. Положительные числа от 0,100 х 10"" до 0,999 х 10".
7. Положительные числа больше 0,999 х 10".
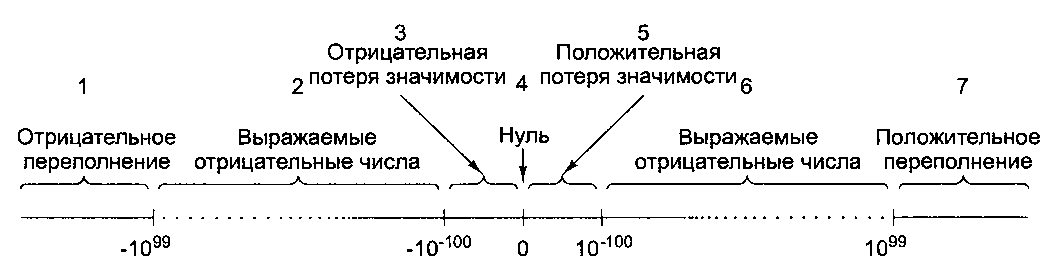
Рис. Б.1. Ось действительных чисел разбита на 7 областей
Первое отличие действительных чисел от чисел с плавающей точкой, которые записываются тремя разрядами в мантиссе и двумя разрядами в экспоненте, состоит в том, что последние нельзя использовать для записи чисел из областей 1, 3, 5 и 7. Если в результате арифметической операции получится число из области 1 или 7 (например, 1060 х 1060 = 10120), то произойдет ошибка переполнения и результат будет неверным. Причина — ограничение области значений чисел в данном представлении. Точно так же нельзя выразить результат из области 3 или 5. Такая ситуация называется ошибкой потери значимости. Эта ошибка менее серьезна, чем ошибка переполнения, поскольку часто нуль является вполне удовлетворительным приближением для чисел из областей 3 или 5. Остаток счета в банке на 10~102 не сильно отличается от нулевого остатка счета.
Второе важное отличие чисел с плавающей точкой от действительных чисел — их плотность. Между любыми двумя действительными числами х и у существует другое действительное число независимо от того, насколько близко к у расположено число х. Это свойство вытекает из того, что для любых отличных действительных чисел х и у между ними существует действительное число г = (х + у)/2. Действительные числа формируют континуум.
Числа с плавающей точкой континуума не формируют. В двухзнаковой пятиразрядной системе можно выразить ровно 179 100 положительных чисел, 179 100 отрицательных чисел и 0 (который можно выразить разными способами), то есть всего 358 201 чисел. Из бесконечного числа действительных чисел в диапазоне от -10+10° до +0,999 х 10" в этой системе можно выразить только 358 201 число. На рис. Б.1 эти числа показаны точками. Результат вычислений может быть и другим числом, даже если он находится в области 2 или 6. Например, результат деления числа +0,100 х 103 на 3 нельзя выразить точно в нашем представлении. Если полученное число нельзя выразить с помощью используемого представления, нужно брать ближайшее представимое число. Такой процесс называется округлением.