Чистая дисконтированная стоимость превышает текущую стоимость доходов: Как рассчитать NPV быстро и правильно: формула, примеры, инструкция
Дисконтированная стоимость (PV) — что это. Формула и пример расчета в Excel
Оба понятия из заголовка этого раздела, дисконтированная (приведенная) стоимость, ПС (presentvalue, или PV), и чистая дисконтированная (приведенная) стоимость, ЧПС (netpresentvalue, или NPV), обозначают текущую стоимость ожидаемых в будущем денежных поступлений.
В качестве примера рассмотрим оценку инвестиции, обещающей доход 100 долл. в год в конце нынешнего и еще четырех следующих лет. Предполагаем, что эта серия из пяти платежей по 100 долл. каждый гарантирована и деньги непременно поступят. Если бы банк платил нам годовой процент в размере 10% при депозите на пять лет, то эти десять процентов как раз и составляли бы альтернативную стоимость инвестиции — эталонную норму прибыли, с которой мы сравнивали бы выгоду от нашего вложения.
Можно вычислить ценность инвестиции путем дисконтирования денежных поступлений от нее с использованием альтернативной стоимости в качестве ставки дисконтирования.
Формула расчета в Excel дисконтированной (приведенной) стоимости (PV) = ЧПС(C1;B5:B9)
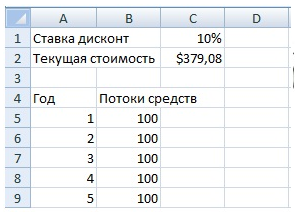
Приведенная стоимость (ПС) в объеме 379,08 долл. и есть текущая стоимость инвестиции.
★ Инвестиционная оценка в Excel. Расчет NPV, IRR, DPP, PI за 5 минут
Предположим, что данная инвестиция продавалась бы за 400 долл. Очевидно, она не стоила бы запрашиваемой цены, поскольку — при условии альтернативного дохода (учетной ставки) в размере 10% — реальная стоимость этого капиталовложения составляла бы только 379,08 долл. Здесь как раз уместно ввести понятие чистой приведенной стоимости (ЧПС). Обозначая символом r учетную ставку для данной инвестиции, получаем следующую формулу NPV:
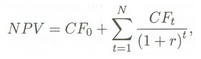
Где СFt – денежное поступление от инвестиции в момент t; CF0 –поток средств (поступление) на текущий момент.
Формула расчета в Excel чистой дисконтированной (приведенной) стоимости (NPV) = ЧПС(C1;B6:B10)+B5
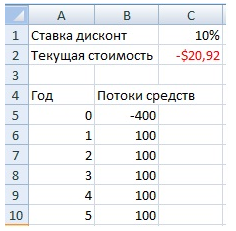
Терминология Excel, касающаяся дисконтируемых потоков денежных средств, несколько отличается от стандартной финансовой терминологии. В Excel сокращение МУР (ЧПС) обозначает приведенную стоимость (а не чистую приведенную стоимость) серии денежных поступлений.
Чтобы рассчитать в Excel чистую приведенную стоимость серии денежных поступлений в обычном понимании финансовой теории, необходимо сначала вычислить приведенную стоимость будущих денежных поступлений (с использованием такой функции Excel, как “ЧПС”), а затем вычесть из этого числа денежный поток на начальный момент времени. (Эта величина часто совпадает со стоимостью рассматриваемого актива.)
Автор: к.э.н. Жданов Иван Юрьевич
Чистая приведённая стоимость — Википедия
Чистая приведённая стоимость (ЧПС, чистая текущая стоимость, чистый дисконтированный доход, ЧДД, англ. Net present value, принятое в международной практике для анализа инвестиционных проектов сокращение — NPV) — это сумма дисконтированных значений потока платежей, приведённых к сегодняшнему дню.
Показатель NPV представляет собой разницу между всеми денежными притоками и оттоками, приведёнными к текущему моменту времени (моменту оценки инвестиционного проекта). Он показывает величину денежных средств, которую инвестор ожидает получить от проекта, после того, как денежные притоки окупят его первоначальные инвестиционные затраты и периодические денежные оттоки, связанные с осуществлением проекта. Поскольку денежные платежи оцениваются с учётом их временно́й стоимости и рисков, NPV можно интерпретировать как стоимость, добавляемую проектом. Её также можно интерпретировать как общую прибыль инвестора.
Иначе говоря, для потока платежей CF (Cash Flow), где CFt{\displaystyle CF_{t}} — платёж через t{\displaystyle t} лет (t=1,…,N{\displaystyle t=1,…,N}) и начальной инвестиции IC (Invested Capital) в размере IC=−CF0{\displaystyle IC=-CF_{0}} чистая приведённая стоимость NPV{\displaystyle NPV} рассчитывается по формуле:
NPV=∑t=0NCFt(1+i)t=−IC+∑t=1NCFt(1+i)t{\displaystyle NPV=\sum _{t=0}^{N}{\frac {CF_{t}}{(1+i)^{t}}}=-IC+\sum _{t=1}^{N}{\frac {CF_{t}}{(1+i)^{t}}}},
где i{\displaystyle i} — ставка дисконтирования.
В обобщённом варианте, инвестиции также должны дисконтироваться, так как в реальных проектах они осуществляются не одномоментно (в нулевом периоде), а растягиваются на несколько периодов. Расчёт ЧПС — стандартный метод оценки эффективности инвестиционного проекта и показывает оценку эффекта от инвестиции, приведённую к настоящему моменту времени с учётом разной временно́й стоимости денег. Если ЧПС больше 0, то инвестиция экономически эффективна, а если ЧПС меньше 0, то инвестиция экономически невыгодна (то есть альтернативный проект, доходность которого принята в качестве ставки дисконтирования требует меньших инвестиций для получения аналогичного потока доходов).
С помощью ЧПС можно также оценивать сравнительную эффективность альтернативных вложений (при одинаковых начальных вложениях более выгоден проект с наибольшим ЧПС). Но всё же для сравнительного анализа более применимыми являются относительные показатели. Применительно к анализу инвестиционных проектов таким показателем является внутренняя норма доходности.
В отличие от показателя дисконтированной стоимости при расчёте чистого дисконтированного дохода учитывается начальная инвестиция. Поэтому формула чистого дисконтированного дохода отличается от формулы дисконтированной стоимости на величину начальной инвестиции IC=−CF0{\displaystyle IC=-CF_{0}}.
Достоинства и недостатки
Положительные свойства ЧПС:
- Чёткие критерии принятия решений.
- Показатель учитывает стоимость денег во времени (используется коэффициент дисконтирования в формулах).
- Показатель учитывает риски проекта посредством различных ставок дисконтирования. Бо́льшая ставка дисконтирования соответствует бо́льшим рискам, меньшая — меньшим.
Отрицательные свойства ЧПС:
- В руководстве ЮНИДО критикуется использование NPV для сравнения эффективности альтернативных проектов (Беренс, Хавранек, 1995, стр.240). Для устранения этого недостатка NPV был разработан индекс скорости удельного прироста стоимости (Коган, 2012).
- Во многих случаях корректный расчёт ставки дисконтирования является проблематичным, что особенно характерно для многопрофильных проектов, которые оцениваются с использованием NPV.
- Хотя все денежные потоки (коэффициент дисконтирования может включать в себя инфляцию, однако зачастую это всего лишь норма прибыли, которая закладывается в расчётный проект) являются прогнозными значениями, формула не учитывает вероятность исхода события.
Для того чтобы оценить проект с учётом вероятности исхода событий поступают следующим образом:
Выделяют ключевые исходные параметры. Каждому параметру устанавливают ряд значений с указанием вероятности наступления события. Для каждой совокупности параметров рассчитывается вероятность наступления и NPV. Дальше идёт расчёт математического ожидания. В итоге получаем наиболее вероятностное NPV.
Пример
Корпорация должна решить, следует ли вводить новые линейки продуктов. Новый продукт будет иметь расходы на запуск, эксплуатационные расходы, а также входящие денежные потоки в течение шести лет. Этот проект будет иметь немедленный (T = 0) отток денежных средств в размере $ 100 000 (которые могут включать в себя механизмы, а также расходы на обучение персонала). Другие оттоки денежных средств за 1-6 лет ожидаются в размере $ 5000 в год. Приток денежных средств, как ожидается, составит $ 30 000 за каждый год 1-6. Как только компания получает прибыль от реализации проекта (например, $ 25 000 после первого года), она кладёт их в банк под 10 % годовых на оставшееся до конца проекта время (то есть на оставшиеся 5 лет для первых $ 25 000). Все денежные потоки после уплаты налогов, и на 7 год никаких денежных потоков не планируется. Ставка дисконтирования составляет 10 %.
Таким образом, требуется оценить, какая сумма больше:
- 100000⋅(1+0.1)t≶∑i=1tpi⋅(1+0.1)(t−i){\displaystyle 100\,000\cdot (1+0.1)^{t}\lessgtr \sum _{i=1}^{t}p_{i}\cdot (1+0.1)^{(t-i)}}, где pi{\displaystyle p_{i}} — доход от проекта, полученный в i-й год реализации проекта, t — общая длительность проекта. Поделим обе части на (1+0.1)t{\displaystyle (1+0.1)^{t}}:
- 100000≶∑i=1tpi⋅(1+0.1)(−i){\displaystyle 100\,000\lessgtr \sum _{i=1}^{t}p_{i}\cdot (1+0.1)^{(-i)}}.
Каждое слагаемое в правой части неравенства — это приведённая стоимость денег по годам. Например, $ 25 000, полученные от реализации проекта после первого года и положенные в банк на 5 лет, дадут такой же доход, как $ 22 727, положенные в банк в начальный момент времени на 6 лет. Таким образом, приведённая стоимость (PV) может быть рассчитана по каждому году:
Сумма всех этих значений является настоящей чистой приведённой стоимостью, которая равна $ 8881.52. Поскольку NPV больше нуля, то было бы лучше инвестировать в проект, чем класть деньги в банк (под 10 % годовых с капитализацией процентов), и корпорации должны вкладывать средства в этот проект, если нет альтернативы с более высоким NPV.
Тот же пример с формулами в Excel:
- NPV (ставка, net_inflow) + initial_investment
- PV (ставка, year_number, yearly_net_inflow)
При более реалистичных проблемах необходимо будет рассмотреть другие факторы, как расчет налогов, неравномерный денежный поток и ценности, а также наличие альтернативных возможностей для инвестиций.
Кроме того, если мы будем использовать формулы, упомянутые выше, для расчёта NPV — то мы видим, что входящие потоки (притоки) денежных средств являются непрерывными и имеют такую же сумму; и подставив значения в формулу
- 1−(1+i)−ni{\displaystyle {\frac {1-(1+i)^{-n}}{i}}} мы получим 1−(1+0.1)−60.1=4.3553{\displaystyle {\frac {1-(1+0.1)^{-6}}{0.1}}=4.3553}.
И если умножить полученное значение на денежные потоки (CF), и учесть первоначальные затраты, то в итоге вычислим чистую приведённую стоимость (NPV):
- [4.3553(30000−5000)]−100000=$8881.52{\displaystyle [4.3553\,(30\,000-5000)]-100\,000=\$\,8\,881.52}
Поскольку NPV больше нуля, то было бы лучше инвестировать в проект, чем ничего не делать, и корпорации должны вкладывать средства в этот проект, если нет альтернативы с более высоким NPV.
Сравнение эффективности альтернативных проектов
Использование NPV может привести к ошибке при сравнении эффективности разнопараметрических инвестиционных проектов и при формировании портфеля инвестиционных проектов. Под разнопараметрическими понимаются такие проекты, у которых одновременно отличаются три инвестиционных параметра: сумма инвестиций, расчётный период и ежегодные финансовые результаты (Коган, 2012).
Покажем это на следующем примере. Сравним эффективность покупки векселя А и векселя В. Эти сделки можно рассматривать как простейшие инвестиционные проекты с единственным оттоком и единственным притоком. Вексель А стоит 100 тыс.р., его выкупят через три года, заплатив при этом 150 тыс.р. Вексель В стоит 50 тыс.р., его выкупят через два года, заплатив при этом 70 тыс. р. При ставке дисконта 10 %, NPVA{\displaystyle NPV^{A}}= 12,7 тыс.р., что больше, чем NPVB{\displaystyle NPV^{B}}=7,85 тыс.р.
Таким образом, по NPV, проект А эффективнее проекта В. Казалось бы, инвестору выгоднее покупать векселя типа А. Однако, представим, что этот инвестор купит два векселя В. При этом он потратит те же 100 тыс.р., что и для покупки векселя А, но выгод получит больше: NPVB+B{\displaystyle NPV^{B+B}}= 15,7 тыс.р. таким образом, инвестиции в векселя типа В выгоднее, чем инвестиции в векселя типа А.
Эти два проекта отличаются не только по суммам инвестиций, но и по расчётным периодам: покупка векселя А — трёхлетний проект, покупка векселя В — двухлетний проект. Если добавить в анализ и этот фактор, то покупка векселя А выглядит ещё менее выгодной. Так, инвестор, имеющий только 100 тыс.р., за шесть лет сможет только дважды купить вексель типа А (NPV этих двух сделок составит 22,24 тыс.р.), но трижды по два векселя типа В (NPV этих шести сделок составит 39,4 тыс.р.). Таким образом, в результате включения в анализ суммы инвестиций и расчётного периода проектов, векселя типа В выглядят ещё более эффективными, чем векселя типа А.
Из данного примера следует вывод, что для корректного анализа эффективности инвестиций, необходимо учитывать три фактора: NPV, сумму инвестиций и расчётный период проекта. Все эти факторы объединены в индекс скорости удельного прироста стоимости, поэтому при использовании этого показателя не возникают вышеуказанные проблемы.
См. также
Ссылки
- NPV — Чистая текущая стоимость Пример расчёта, определение, характеристика, формула, условия сравнения, критерий приемлемости, недостатки.
- Беренс В., Хавранек П. М. Руководство по подготовке промышленных технико-экономических исследований/Пер. с англ. перераб. и дополн. изд. — М.: АОЗТ «Интерэксперт», 1995. — 343 с: табл., граф.
- Виленский П. Л., Лившиц В. Н., Смоляк С. А. Оценка эффективности инвестиционных проектов. Теория и практика. — М.: Дело, 2008. — 1104 с. — ISBN 978-5-7749-0518-8.
- Коган А. Б. Новации оценки локальной и глобальной эффективности реальных инвестиций: монография / А. Б. Коган ; Новосиб. гос. архитектур.-строит. ун-т (Сибстрин). — Новосибирск : НГАСУ (Сибстрин), 2012. — 95 с.
- Четыркин Е. М. Финансовая математика. — М.: Дело, 2008. — 400 с. — ISBN 978-5-7749-0504-1.
Чистая приведённая стоимость — Википедия
Чистая приведённая стоимость (ЧПС, чистая текущая стоимость, чистый дисконтированный доход, ЧДД, англ. Net present value, принятое в международной практике для анализа инвестиционных проектов сокращение — NPV) — это сумма дисконтированных значений потока платежей, приведённых к сегодняшнему дню.
Показатель NPV представляет собой разницу между всеми денежными притоками и оттоками, приведёнными к текущему моменту времени (моменту оценки инвестиционного проекта). Он показывает величину денежных средств, которую инвестор ожидает получить от проекта, после того, как денежные притоки окупят его первоначальные инвестиционные затраты и периодические денежные оттоки, связанные с осуществлением проекта. Поскольку денежные платежи оцениваются с учётом их временно́й стоимости и рисков, NPV можно интерпретировать как стоимость, добавляемую проектом. Её также можно интерпретировать как общую прибыль инвестора.
Иначе говоря, для потока платежей CF (Cash Flow), где CFt{\displaystyle CF_{t}} — платёж через t{\displaystyle t} лет (t=1,…,N{\displaystyle t=1,…,N}) и начальной инвестиции IC (Invested Capital) в размере IC=−CF0{\displaystyle IC=-CF_{0}} чистая приведённая стоимость NPV{\displaystyle NPV} рассчитывается по формуле:
NPV=∑t=0NCFt(1+i)t=−IC+∑t=1NCFt(1+i)t{\displaystyle NPV=\sum _{t=0}^{N}{\frac {CF_{t}}{(1+i)^{t}}}=-IC+\sum _{t=1}^{N}{\frac {CF_{t}}{(1+i)^{t}}}},
где i{\displaystyle i} — ставка дисконтирования.
В обобщённом варианте, инвестиции также должны дисконтироваться, так как в реальных проектах они осуществляются не одномоментно (в нулевом периоде), а растягиваются на несколько периодов. Расчёт ЧПС — стандартный метод оценки эффективности инвестиционного проекта и показывает оценку эффекта от инвестиции, приведённую к настоящему моменту времени с учётом разной временно́й стоимости денег. Если ЧПС больше 0, то инвестиция экономически эффективна, а если ЧПС меньше 0, то инвестиция экономически невыгодна (то есть альтернативный проект, доходность которого принята в качестве ставки дисконтирования требует меньших инвестиций для получения аналогичного потока доходов).
С помощью ЧПС можно также оценивать сравнительную эффективность альтернативных вложений (при одинаковых начальных вложениях более выгоден проект с наибольшим ЧПС). Но всё же для сравнительного анализа более применимыми являются относительные показатели. Применительно к анализу инвестиционных проектов таким показателем является внутренняя норма доходности.
В отличие от показателя дисконтированной стоимости при расчёте чистого дисконтированного дохода учитывается начальная инвестиция. Поэтому формула чистого дисконтированного дохода отличается от формулы дисконтированной стоимости на величину начальной инвестиции IC=−CF0{\displaystyle IC=-CF_{0}}.
Достоинства и недостатки
Положительные свойства ЧПС:
- Чёткие критерии принятия решений.
- Показатель учитывает стоимость денег во времени (используется коэффициент дисконтирования в формулах).
- Показатель учитывает риски проекта посредством различных ставок дисконтирования. Бо́льшая ставка дисконтирования соответствует бо́льшим рискам, меньшая — меньшим.
Отрицательные свойства ЧПС:
- В руководстве ЮНИДО критикуется использование NPV для сравнения эффективности альтернативных проектов (Беренс, Хавранек, 1995, стр.240). Для устранения этого недостатка NPV был разработан индекс скорости удельного прироста стоимости (Коган, 2012).
- Во многих случаях корректный расчёт ставки дисконтирования является проблематичным, что особенно характерно для многопрофильных проектов, которые оцениваются с использованием NPV.
- Хотя все денежные потоки (коэффициент дисконтирования может включать в себя инфляцию, однако зачастую это всего лишь норма прибыли, которая закладывается в расчётный проект) являются прогнозными значениями, формула не учитывает вероятность исхода события.
Для того чтобы оценить проект с учётом вероятности исхода событий поступают следующим образом:
Выделяют ключевые исходные параметры. Каждому параметру устанавливают ряд значений с указанием вероятности наступления события. Для каждой совокупности параметров рассчитывается вероятность наступления и NPV. Дальше идёт расчёт математического ожидания. В итоге получаем наиболее вероятностное NPV.
Пример
Корпорация должна решить, следует ли вводить новые линейки продуктов. Новый продукт будет иметь расходы на запуск, эксплуатационные расходы, а также входящие денежные потоки в течение шести лет. Этот проект будет иметь немедленный (T = 0) отток денежных средств в размере $ 100 000 (которые могут включать в себя механизмы, а также расходы на обучение персонала). Другие оттоки денежных средств за 1-6 лет ожидаются в размере $ 5000 в год. Приток денежных средств, как ожидается, составит $ 30 000 за каждый год 1-6. Как только компания получает прибыль от реализации проекта (например, $ 25 000 после первого года), она кладёт их в банк под 10 % годовых на оставшееся до конца проекта время (то есть на оставшиеся 5 лет для первых $ 25 000). Все денежные потоки после уплаты налогов, и на 7 год никаких денежных потоков не планируется. Ставка дисконтирования составляет 10 %.
Таким образом, требуется оценить, какая сумма больше:
- 100000⋅(1+0.1)t≶∑i=1tpi⋅(1+0.1)(t−i){\displaystyle 100\,000\cdot (1+0.1)^{t}\lessgtr \sum _{i=1}^{t}p_{i}\cdot (1+0.1)^{(t-i)}}, где pi{\displaystyle p_{i}} — доход от проекта, полученный в i-й год реализации проекта, t — общая длительность проекта. Поделим обе части на (1+0.1)t{\displaystyle (1+0.1)^{t}}:
- 100000≶∑i=1tpi⋅(1+0.1)(−i){\displaystyle 100\,000\lessgtr \sum _{i=1}^{t}p_{i}\cdot (1+0.1)^{(-i)}}.
Каждое слагаемое в правой части неравенства — это приведённая стоимость денег по годам. Например, $ 25 000, полученные от реализации проекта после первого года и положенные в банк на 5 лет, дадут такой же доход, как $ 22 727, положенные в банк в начальный момент времени на 6 лет. Таким образом, приведённая стоимость (PV) может быть рассчитана по каждому году:
Сумма всех этих значений является настоящей чистой приведённой стоимостью, которая равна $ 8881.52. Поскольку NPV больше нуля, то было бы лучше инвестировать в проект, чем класть деньги в банк (под 10 % годовых с капитализацией процентов), и корпорации должны вкладывать средства в этот проект, если нет альтернативы с более высоким NPV.
Тот же пример с формулами в Excel:
- NPV (ставка, net_inflow) + initial_investment
- PV (ставка, year_number, yearly_net_inflow)
При более реалистичных проблемах необходимо будет рассмотреть другие факторы, как расчет налогов, неравномерный денежный поток и ценности, а также наличие альтернативных возможностей для инвестиций.
Кроме того, если мы будем использовать формулы, упомянутые выше, для расчёта NPV — то мы видим, что входящие потоки (притоки) денежных средств являются непрерывными и имеют такую же сумму; и подставив значения в формулу
- 1−(1+i)−ni{\displaystyle {\frac {1-(1+i)^{-n}}{i}}} мы получим 1−(1+0.1)−60.1=4.3553{\displaystyle {\frac {1-(1+0.1)^{-6}}{0.1}}=4.3553}.
И если умножить полученное значение на денежные потоки (CF), и учесть первоначальные затраты, то в итоге вычислим чистую приведённую стоимость (NPV):
- [4.3553(30000−5000)]−100000=$8881.52{\displaystyle [4.3553\,(30\,000-5000)]-100\,000=\$\,8\,881.52}
Поскольку NPV больше нуля, то было бы лучше инвестировать в проект, чем ничего не делать, и корпорации должны вкладывать средства в этот проект, если нет альтернативы с более высоким NPV.
Сравнение эффективности альтернативных проектов
Использование NPV может привести к ошибке при сравнении эффективности разнопараметрических инвестиционных проектов и при формировании портфеля инвестиционных проектов. Под разнопараметрическими понимаются такие проекты, у которых одновременно отличаются три инвестиционных параметра: сумма инвестиций, расчётный период и ежегодные финансовые результаты (Коган, 2012).
Покажем это на следующем примере. Сравним эффективность покупки векселя А и векселя В. Эти сделки можно рассматривать как простейшие инвестиционные проекты с единственным оттоком и единственным притоком. Вексель А стоит 100 тыс.р., его выкупят через три года, заплатив при этом 150 тыс.р. Вексель В стоит 50 тыс.р., его выкупят через два года, заплатив при этом 70 тыс. р. При ставке дисконта 10 %, NPVA{\displaystyle NPV^{A}}= 12,7 тыс.р., что больше, чем NPVB{\displaystyle NPV^{B}}=7,85 тыс.р.
Таким образом, по NPV, проект А эффективнее проекта В. Казалось бы, инвестору выгоднее покупать векселя типа А. Однако, представим, что этот инвестор купит два векселя В. При этом он потратит те же 100 тыс.р., что и для покупки векселя А, но выгод получит больше: NPVB+B{\displaystyle NPV^{B+B}}= 15,7 тыс.р. таким образом, инвестиции в векселя типа В выгоднее, чем инвестиции в векселя типа А.
Эти два проекта отличаются не только по суммам инвестиций, но и по расчётным периодам: покупка векселя А — трёхлетний проект, покупка векселя В — двухлетний проект. Если добавить в анализ и этот фактор, то покупка векселя А выглядит ещё менее выгодной. Так, инвестор, имеющий только 100 тыс.р., за шесть лет сможет только дважды купить вексель типа А (NPV этих двух сделок составит 22,24 тыс.р.), но трижды по два векселя типа В (NPV этих шести сделок составит 39,4 тыс.р.). Таким образом, в результате включения в анализ суммы инвестиций и расчётного периода проектов, векселя типа В выглядят ещё более эффективными, чем векселя типа А.
Из данного примера следует вывод, что для корректного анализа эффективности инвестиций, необходимо учитывать три фактора: NPV, сумму инвестиций и расчётный период проекта. Все эти факторы объединены в индекс скорости удельного прироста стоимости, поэтому при использовании этого показателя не возникают вышеуказанные проблемы.
См. также
Ссылки
- NPV — Чистая текущая стоимость Пример расчёта, определение, характеристика, формула, условия сравнения, критерий приемлемости, недостатки.
- Беренс В., Хавранек П. М. Руководство по подготовке промышленных технико-экономических исследований/Пер. с англ. перераб. и дополн. изд. — М.: АОЗТ «Интерэксперт», 1995. — 343 с: табл., граф.
- Виленский П. Л., Лившиц В. Н., Смоляк С. А. Оценка эффективности инвестиционных проектов. Теория и практика. — М.: Дело, 2008. — 1104 с. — ISBN 978-5-7749-0518-8.
- Коган А. Б. Новации оценки локальной и глобальной эффективности реальных инвестиций: монография / А. Б. Коган ; Новосиб. гос. архитектур.-строит. ун-т (Сибстрин). — Новосибирск : НГАСУ (Сибстрин), 2012. — 95 с.
- Четыркин Е. М. Финансовая математика. — М.: Дело, 2008. — 400 с. — ISBN 978-5-7749-0504-1.
Задача №1871 (чистая дисконтированная стоимость и внутренняя норма доходности)
Если чистая дисконтированная стоимость проекта отрицательна, то это означает, что:
- а) внутренняя норма доходности ниже ставки дисконтирования;
- б) внутренняя норма доходности выше ставки дисконтирования;
- в) внутренняя норма доходности равна ставке дисконтирования.
Объясните свой выбор.
Рекомендуемые задачи по дисциплине
Решение задачи:
Внутренняя норма доходности (IRR) – это коэффициент, показывающий максимально допустимый риск по инвестиционному проекту или минимальный приемлемый уровень доходности. Внутренняя норма доходности равна ставке дисконтирования, при которой чистый дисконтированный доход отсутствует, то есть равен нулю.
Данный показатель используется для оценки привлекательности инвестиционного проекта или для сопоставительного анализа с другими проектами. Для этого IRR сравнивают с эффективной ставкой дисконтирования, то есть с требуемым уровнем доходности проекта (r):
| Значение IRR | Вывод |
| IRR больше r | Инвестиционный проект имеет внутреннюю норму доходности выше чем затраты на собственный и заемный капитал. Данный проект следует принять для дальнейшего анализа (при этом чистая дисконтированная стоимость проекта положительная) |
| IRR меньше r | Инвестиционный проект имеет норму доходности ниже чем затраты на капитал, это свидетельствует о нецелесообразности вложения в него (при этом чистая дисконтированная стоимость проекта отрицательная) |
| IRR=r | Внутренняя доходность проекта равна стоимости капитала, проект находится на минимально допустимом уровне и следует произвести корректировки движения денежных средств и увеличить денежные потоки (при этом чистая дисконтированная стоимость проекта равна нулю) |
Таким образом, если чистая дисконтированная стоимость проекта отрицательна, то это означает, что IRR меньше r, т.е. внутренняя норма доходности ниже ставки дисконтирования. Ответ – а.
Метод чистой приведенной стоимости| Определение и формула чистой приведенной стоимости Стратегический финансовый директор
24 июля
Вернуться домой
Метод чистой приведенной стоимости
См. Также:
Методы оценки
Метод скорректированной приведенной стоимости
Метод внутренней нормы прибыли
Временная стоимость денег
Капитал Методы составления бюджета
Правило 72
Чистая приведенная стоимость (ЧПС) определяется как приведенная стоимость будущих чистых денежных потоков от инвестиционного проекта.NPV — один из основных способов оценки инвестиций. Метод чистой приведенной стоимости — один из наиболее часто используемых методов; поэтому это общий термин в сознании любого опытного делового человека.
Чтобы повысить ценность вашей компании, выявляйте и находите решения для тех «разрушителей» ценности. Нажмите кнопку, чтобы бесплатно загрузить «10 самых ценных разрушителей».
Скачать 10 лучших разрушителей стоимости
Метод чистой текущей стоимости Объяснение
Чистую приведенную стоимость можно объяснить довольно просто, хотя процесс применения NPV может быть значительно сложнее.Анализ чистой приведенной стоимости исключает элемент времени при сравнении альтернативных инвестиций. Кроме того, метод NPV обычно обеспечивает более правильные решения, чем другие методы при капитальных вложениях. Следовательно, это более популярный метод оценки проектов капитального бюджета.
При выборе между конкурирующими инвестициями с использованием расчета чистой приведенной стоимости следует выбрать тот, который имеет наибольшую приведенную стоимость.
Если:
NPV> 0, принять вложение.
NPV <0, отклонить вложение.
NPV = 0, инвестиции являются маржинальными.
Ставка дисконтирования чистой приведенной стоимости
Наиболее важной переменной для принятия решения при применении метода чистой приведенной стоимости является выбор соответствующей ставки дисконтирования. Обычно следует использовать либо средневзвешенную стоимость капитала для компании, либо норму доходности альтернативных инвестиций. Как правило, чем выше ставка дисконтирования, тем ниже чистая приведенная стоимость при прочих равных условиях.Кроме того, при установлении ставки дисконтирования следует применять элемент риска. Более рискованные инвестиции должны иметь более высокую ставку дисконтирования, чем безопасные инвестиции. Для более длительных инвестиций следует использовать более высокую ставку дисконтирования, чем для краткосрочных проектов. Аналогично ставкам на кривой доходности казначейских векселей.
Прочие ставка дисконтирования чистой приведенной стоимости Факторы включают: Какие ставки дисконтирования следует использовать до налогообложения или после налогообложения? Как правило, если вы используете чистые денежные потоки до налогообложения, используйте ставки дисконтирования до налогообложения.Чистый денежный поток после уплаты налогов следует использовать по ставке дисконтирования после уплаты налогов.
Формула чистой приведенной стоимости
Формула чистой приведенной стоимости для отдельной инвестиции: NPV = PV минус I
Где:
PV = текущая стоимость
I = инвестиции
NPV = чистая приведенная стоимость
Чистая Формула приведенной стоимости для множественных инвестиций:
Сумма всех условий:
CF (денежный поток) / (1 + r) t
Где:
CF = единовременный денежный поток
r = ставка дисконтирования
t = время движения денежных средств
Расчет чистой приведенной стоимости
Для однократной инвестиции :
120 000 — 5000 долларов = 115 000 долларов
Где:
PV = 120 000 долларов
I = 5000 долларов
NPV = 115 000 долларов США
Для множественных инвестиций :
120 000 долларов США / (1 + 10%) 1 = 109 091 долларов США
Где:
CF = 120 000 долларов США
r = 10%
t = 1 год
NPV = 109 091 долларов США
[ box] Как вы рассчитываете Уважая чистую приведенную стоимость, убедитесь, что нет других «разрушителей», которые могут снизить стоимость вашей компании.Загрузите бесплатно «10 лучших разрушителей стоимости». [/ Box]
Преимущества чистой приведенной стоимости
Преимущества чистой приведенной стоимости включают следующее:
Ограничения чистой приведенной стоимости
Недостатки чистой приведенной стоимости включают следующее :
Пример чистой приведенной стоимости
Например, Джоди является владельцем фирмы по взысканию долгов под названием Collectco. Джоди работал в своей компании несколько лет. По мере того, как у Джоди нарастали годы, у него появилось желание уйти на пенсию и жить более простой жизнью.Наконец, достигнув конца своей веревки, Джоди готов двигаться дальше и проводить больше времени со своими детьми. Для этого Джоди должен продать свою компанию. Кроме того, Джоди должен сначала убедиться, что его компания соответствует отраслевым стандартам. Если компания Джоди не будет работать с той же эффективностью, что и отраслевой стандарт, он потеряет часть своей стоимости в переговорах с покупателем.
Джоди начинает с найма опытного консультанта в отрасли для проведения аудита компании.Проверка оказалась намного лучше, чем ожидал Джоди. Но, несмотря на это, Джоди должен обновить программное обеспечение своих коллекций, поскольку оно больше не поддерживается технической помощью создателя. Джоди выполняет расчет чистой приведенной стоимости для оценки этих инвестиций.
120 000 — 5000 долларов = 115 000 долларов
Где:
PV = Годовой доход Collectco = 120 000 долларов
I = Стоимость нового программного обеспечения для коллекций = 5000 долларов
NPV = 115 000 долларов
Теперь Джоди может начать процесс поиска покупатель для своей компании.Его консультант, эксперт по ведению бизнеса коллекторских фирм, говорит ему, что в его интересах знать чистую приведенную стоимость своей компании до того, как он начнет переговоры. Итак, Джоди начинает этот процесс с попытки найти самый простой способ выполнить это вычисление. Найдя несколько релевантных онлайн-результатов по запросу «калькулятор чистой приведенной стоимости», Джоди находит формулу NPV. Затем Джоди выполняет следующий расчет:
120 000 долл. США / (1 + 10%) 1 = 109 091 долл. США
Где:
CF = годовой денежный поток Collectco = 120 000 долл. США
r = 10%
t = 1 год
NPV = 109 091 долл. США
Благодаря этим инвестициям и информации, Джоди может начать достигать того, о чем он всегда мечтал: комфортного выхода на пенсию, который позволяет ему проводить время с людьми, о которых он больше всего заботится.Джоди доволен, потому что все его усилия приводят к той жизни, ради которой он работал.
Если вы похожи на Джоди и хотите найти выход, загрузите 10 лучших разрушителей ценности, чтобы максимизировать ценность вашей компании. Не позволяйте эсминцам отбирать у вас деньги!


[box] Дополнительный член лаборатории стратегического финансового директора
Получите доступ к плану выполнения настройки денежного потока в лаборатории SCFO. Этот инструмент позволяет вам количественно оценить наличные деньги, разблокированные в вашей компании.
Щелкните здесь , чтобы получить доступ к вашему плану выполнения. Не участник лаборатории?
Щелкните здесь , чтобы узнать больше о SCFO Labs [/ box]


Шаблон чистой приведенной стоимости
Шаблон превосходной чистой приведенной стоимости можно найти на сайте Microsoft Office здесь: http: // office. microsoft.com/en-us/templates/TC100152681033.aspx
.Чистая приведенная стоимость
Как поясняют финансовые авторы, чистая приведенная стоимость или Чистая текущая стоимость определяется как приведенная стоимость отдельных денежных потоков, как входящих, так и исходящих, хозяйствующего субъекта. Чистая приведенная стоимость (NPV), в основном, используется при составлении бюджета капиталовложений для изучения прибыльности проекта или инвестиций. Однако анализ NPV зависит от надежности будущих денежных поступлений, которые будут получены в результате реализации проекта или инвестиционного плана.
Расчет (формула)
T — количество лет,
C t — выручка (входящий денежный поток) за год t,
C o — первоначальные затраты (исходящий денежный поток).
В дополнение к вышеупомянутой формуле, NPV также можно рассчитать с помощью таблиц и электронных таблиц, таких как MS Excel.
Любой перспективный проект будет считаться приемлемым, если он имеет положительную ЧПС, и такой же может быть отклонен, если он содержит отрицательную ЧПС.Например, возьмем случай, когда предприятие розничной торговли одеждой желает купить уже существующий магазин. В рамках этого процесса покупатель сначала анализирует будущий денежный поток, который будет генерироваться магазином. После этого эти денежные потоки дисконтируются до общей суммы приведенной стоимости, скажем, 655 000 долларов. Если, в случае, владелец магазина готов продать свой бизнес за меньшую сумму, покупатель, вероятно, примет предложение, поскольку оно отражает положительную инвестицию в NPV.
Напротив, если владелец магазина не желает продавать его за меньшую сумму, покупатель, вероятно, не купит магазин за эти инвестиции, что может привести к отрицательной чистой приведенной стоимости, что приведет к падению компании в целом. ценность.
Если добавить больше, то расчет NPV чувствителен к ставке дисконтирования. Даже малейшее изменение ставок дисконтирования может привести к большим изменениям чистой приведенной стоимости (NPV). Таким образом, показатели чистой приведенной стоимости весьма неопределенны из-за неопределенного характера ставок дисконтирования. Кроме того, чистая приведенная стоимость также иногда зависит от неопределенных прогнозов о предполагаемых денежных потоках, что создает проблемы при расчете чистой приведенной стоимости.
Что ж, в качестве решения обеих этих проблем можно использовать ряд ставок дисконтирования и прогнозов для расчета диапазона чистой приведенной стоимости, тем самым генерируя наилучшие, наихудшие и медианные значения NPV или распределение вероятностей для чистого настоящего Ценность.
.Напоминание о чистой приведенной стоимости
Большинство людей знают, что деньги, которые у вас есть сейчас, более ценны, чем деньги, которые вы соберете позже. Это потому, что вы можете использовать его, чтобы заработать больше денег, управляя бизнесом, или покупая что-то сейчас и продавая позже, или просто кладя это в банк и получая проценты. Будущие деньги также менее ценны, потому что инфляция подрывает их покупательную способность. Это называется
Чтобы узнать больше о том, как можно использовать чистую приведенную стоимость для перевода стоимости инвестиций в сегодняшние доллары, я поговорил с Джо Найтом, соавтором книги Financial Intelligence: A Manager’s Guide to Know What the Numbers Really Mean и соучредителем и владелец www.business-literacy.com.
Что такое чистая приведенная стоимость?
«Чистая приведенная стоимость — это текущая стоимость денежных потоков при требуемой норме доходности вашего проекта по сравнению с вашими первоначальными инвестициями», — говорит Найт.На практике это метод расчета рентабельности инвестиций или рентабельности инвестиций в проект или расходы. Посмотрев на все деньги, которые вы ожидаете получить от инвестиций, и переведя эту прибыль в сегодняшние доллары, вы сможете решить, стоит ли проект.
Для чего его обычно используют компании?
Когда менеджеру нужно сравнить проекты и решить, какие из них следует реализовать, обычно доступны три варианта: внутренняя норма прибыли, метод окупаемости и чистая приведенная стоимость.Найт говорит, что чистая приведенная стоимость, часто называемая NPV, является предпочтительным инструментом для большинства финансовых аналитиков. На то есть две причины. Во-первых, NPV учитывает временную стоимость денег , переводя будущие денежные потоки в сегодняшние доллары. Во-вторых, он предоставляет конкретное число, которое менеджеры могут использовать для простого сравнения первоначальных денежных затрат с текущей стоимостью прибыли.
Другой дубль
«Этот метод намного превосходит наиболее часто используемый метод окупаемости», — говорит он.Привлекательность окупаемости заключается в том, что ее легко рассчитать и понять: когда вы вернете вложенные деньги? Но при этом не учитывается, что покупательная способность денег сегодня больше, чем покупательная способность той же суммы денег в будущем.
Вот что делает NPV лучшим методом, — говорит Найт. И, к счастью, с финансовыми калькуляторами и таблицами Excel теперь почти так же легко рассчитать NPV.
Менеджеры также используют NPV, чтобы решить, делать ли крупные покупки, такие как оборудование или программное обеспечение.Она также используется при слияниях и поглощениях (хотя в этом сценарии она называется моделью дисконтированных денежных потоков ). Фактически, это модель, которую Уоррен Баффет использует для оценки компаний. Каждый раз, когда компания использует сегодняшние доллары для получения прибыли в будущем, NPV — это хороший выбор.
Как это рассчитать?
Никто не рассчитывает NPV вручную, говорит Найт. В Excel есть функция ЧПС, которая упрощает задачу после ввода потока затрат и выгод.(Включите «NPV» в функцию «Справка», и вы получите краткое руководство, либо вы можете приобрести HBR Guide to Building Your Business Case + Tools, который включает простую в использовании предварительно заполненную электронную таблицу для NPV и других ROI методы). Многие финансовые калькуляторы также включают функцию NPV. «Такой выродок, как я, у меня он есть на моем iPhone. Мне нравится знать, что он у меня в кармане, — говорит Найт.
Даже если вы не математический ботаник, как Найт, полезно разобраться в математике, стоящей за этим. «Даже опытные аналитики могут не помнить или понимать математику, но это довольно просто», — говорит он.Расчет выглядит так:
Это сумма приведенной стоимости денежных потоков (положительных и отрицательных) за каждый год, связанных с инвестициями, дисконтированная таким образом, чтобы она была выражена в сегодняшних долларах. Чтобы сделать это вручную, вы сначала рассчитываете приведенную стоимость прогнозируемой прибыли на каждый год, взяв прогнозируемый денежный поток на каждый год и разделив его на (1 + ставка дисконтирования). Это выглядит так:
Итак, для денежного потока через пять лет уравнение выглядит следующим образом:
Если проект приносит доход за пять лет, вы рассчитываете эту цифру для каждого из этих пяти лет.Затем сложите их вместе. Это будет текущая стоимость всех ваших прогнозируемых доходов. Затем вы вычитаете свои первоначальные инвестиции из этого числа, чтобы получить NPV.
Если NPV отрицательная, значит проект плохой. В конечном итоге это истощит бизнес. Однако в случае положительного результата проект следует принять. Чем больше положительное число, тем больше выгода для компании.
Теперь вам может быть интересно узнать о ставке дисконтирования. Ставка дисконтирования будет зависеть от конкретной компании, поскольку она связана с тем, как компания получает свои средства.Это норма прибыли, которую ожидают инвесторы, или стоимость заимствования денег. Если акционеры ожидают 12% прибыли, это ставка дисконтирования, которую компания будет использовать для расчета NPV. Если фирма платит 4% годовых по своему долгу, то она может использовать эту цифру в качестве учетной ставки. Обычно ставку устанавливает офис финансового директора.
Какие распространенные ошибки делают люди?
Есть две вещи, о которых менеджеры должны знать при использовании NPV. Во-первых, это бывает трудно объяснить другим.Как пишет Найт в своей книге Financial Intelligence , «дисконтированная стоимость будущих денежных потоков — не такая фраза, которую легко сбить с толку нефинансового языка». Тем не менее, по его словам, стоит приложить дополнительные усилия для объяснения и представления NPV из-за его превосходства как метода. Он пишет: «Любая инвестиция, прошедшая тест на чистую приведенную стоимость, увеличит акционерную стоимость, а любая неудачная инвестиция (если она все равно будет осуществлена) нанесет ущерб компании и ее акционерам».
Дополнительная литература
Второе, о чем следует помнить менеджерам, — это то, что расчеты основаны на нескольких предположениях и оценках, а это означает, что есть много места для ошибок.Вы можете снизить риски, дважды проверив свои оценки и проведя анализ чувствительности после того, как сделаете первоначальный расчет.
Есть три места, где вы можете сделать неверные оценки, которые сильно повлияют на конечные результаты ваших вычислений. Во-первых, это первоначальные вложения. Вы знаете, сколько будет стоить проект или расходы? Если вы покупаете оборудование с четкой ценой, риска нет. Но если вы обновляете свою ИТ-систему и оцениваете время и ресурсы сотрудников, сроки реализации проекта и сумму, которую вы собираетесь платить сторонним поставщикам, цифры могут сильно отличаться.
Во-вторых, существуют риски, связанные со ставкой дисконтирования. Вы используете сегодняшнюю ставку и применяете ее к будущим доходам, поэтому есть вероятность, что, скажем, в третий год проекта процентные ставки вырастут, а стоимость ваших средств вырастет. Это будет означать, что ваши доходы за этот год будут менее ценными, чем вы изначально думали.
В-третьих, и именно здесь, по словам Найта, люди часто делают ошибки при оценке, вы должны быть относительно уверены в предполагаемой доходности вашего проекта.«Эти прогнозы обычно оптимистичны, потому что люди хотят реализовать проект или купить оборудование», — говорит он.
.финансовых формул (с калькуляторами)
Люди из всех слоев общества, от студентов, биржевых маклеров и банкиров; риэлторам, домовладельцам и управляющим находят финансовые формулы невероятно полезными в повседневной жизни. Используете ли вы финансовые формулы для личных или по причинам образования, наличие доступа к правильным финансовым формулам может помочь улучшить вашу жизнь.
Независимо от того, в какой финансовой сфере вы работаете или изучаете, от корпоративных финансов до банковского дела, все они построены на тот же фундамент стандартных формул и уравнений.Хотя некоторые из этих сложных формул могут сбить с толку обычного человека, мы помочь, внося вам ясность.
Имеете ли вы дело со сложными процентами, аннуитетами, акциями или облигациями, инвесторы должны иметь возможность эффективно оценивать уровень ценности или достоинства их финансовых показателей. Это делается путем оценки будущей прибыли и ее расчета относительно текущая стоимость или эквивалентная норма прибыли.
Финансовые формулы.net может помочь.
Финансовая информация и калькуляторы на сайте FinanceFormulas.net предназначены не только для профессионалов, но и для всех, кто потребность в фундаментальных формулах, уравнениях и основных вычислениях, составляющих мир финансов. От студентов колледжа которые изучают финансы и бизнес для профессионалов в области корпоративных финансов, FinanceFormulas.net поможет вам найти финансовые формулы, уравнения и калькуляторы, необходимые для достижения успеха.
Кто может получить больше всего от FinanceFormulas.net?
Студенты, изучающие финансы и бизнес , могут использовать формулы и калькуляторы, бесплатно предоставляемые FinanceFormulas.net в качестве постоянного справочника, во время учебы в школе, затем во время работы в мир финансов.
Люди, уже работающие в сфере бизнеса , которые могут иметь Если вы забыли, как использовать конкретную формулу или набор уравнений, наши инструменты станут бесценным ресурсом.FinanceFormulas.net не только упрощает поиск формулы, уравнения или калькулятора, которые вы ищете, мы упрощаем добавление формулы в закладки, чтобы вы больше никогда не придется тратить время на поиск нужного инструмента.
Любой . Люди любого возраста могут пользоваться калькуляторами в FinanceFormulas.net, чтобы помочь им справляться с финансовыми трудностями повседневной жизни. Ипотека, задолженность по кредитной карте или понимание академической оценки вашего инвестиции, такие как акции и облигации, он имеет доступ к правильным формулам, уравнениям и калькуляторам, которые могут помочь вам проложите свой путь к финансово благополучной жизни.
Планируете ли вы использовать бесплатные формулы, предоставляемые FinanceFormulas.net, для личного или академического использования, FinanceFormulas.net здесь, чтобы помочь вам найти банковские формулы, формулы акций и облигаций, корпоративные и прочие формулы, которые вам нужны.
Вернуться к началу
Об авторе