Чистая приведенная стоимость проекта: Чистая приведенная стоимость

Содержание

Расчет чистой приведенной стоимости (NPV) проекта в 1С:Управление холдингом

Блог

26.07.2021

Рассматривая любой инвестиционный проект, компании стараются оценить его надежность и эффективность, так как, разумеется, заинтересованы не только в окупаемости вложенных средств, но и в получении доп. капитала поверх исходных вложений. Для подобных оценок большинство организаций используют популярный метод расчета NPV (чистая приведенная стоимость). Такой метод диагностики позволяет получить информацию о дисконтированной стоимости при конкретной процентной ставке. Компания наглядно может увидеть разницу между ожидаемой прибылью и всеми расходами на запуск бизнес-проекта.

Благодаря корректному расчету чистой приведенной стоимости организации могут принимать правильные решения о вложениях в тот или иной бизнес-проект.

Пример расчета NPV проекта в 1С:Управление холдингом 8

Представим, что компания «Альфа» собирается провести модернизацию производственного оборудования, за счет чего планируется увеличить производство и, соответственно, реализацию выпущенной продукции.

Плановые показатели движения денежных средств по проекту «Модернизация производственного оборудования» представлены в таблице ниже.

Таблица: Бюджет движений денежных средств в рамках проекта «Модернизации производственного оборудования».

Ставка дисконтирования – 6%;
Задача: рассчитать NPV (чистую приведенную стоимость) проекта

Функциональность 1С:УХ позволяет автоматизировать полный цикл инвестиционных проектов от начала до завершения. Полностью функционал мы рассматривать в этом примере не будем, а рассмотрим возможности автоматического расчета одного из ключевых показателей эффективности проекта – «Чистой приведенной стоимости (NPV)».

Для отражения учета инвестиционных проектов в 1С:УХ нам необходимо:

Создать «Виды бюджетов» для формирования «Бюджета доходов и расходов»; «Бюджета движений денежных средств» и «Бюджета ресурсов», настроить бланки отчетов, в том числе «Сводную таблицу».

Выполнить настройки учета (меню «Общие справочники и настройки» — «Инвестиционные проекты»)

Внести плановые данные по бюджету проекта с помощью «Экземпляров бюджетов».

В справочнике «Проекты» создать проект «Модернизация производственного оборудования».

Далее в системе нужно отразить факт исполнения бюджета. В нашем случае с помощью документа «Отражение фактических данных», который формируется автоматически при проведении первичных документов.

По ходу выполнения проекта пользователь может контролировать ключевые показатели проекта с помощью данных на закладке «Ключевые показатели» в справочнике «Проекты».

Таким образом, нет необходимости вручную настраивать формулы ключевых показателей проектов, достаточно выполнить первоначальные настройки, описанные выше.

После ввода данных с помощью имеющихся инструментов 1С:УХ можно оперативно контролировать выполнение показателей проекта.

NPV важно рассчитывать любой компании, если она не хочет «спустить деньги в трубу». Но и у него есть свои «слабости», поэтому при расчете чистой приведенной стоимости стоит обращать внимание на другие разделы бизнес-плана, сопоставляя количественные характеристики с текущей ситуацией развития компании и возможными перспективами. Таким образом, для того, чтобы инвестиционный анализ был грамотно встроен в содержание бизнес-процессов, нужен комплексный подход.

Как вычислять и анализировать чистую приведенную стоимость (NPV)? | статьи

Деньги, которыми вы располагаете сейчас, представляют большую ценность, чем деньги, которые у вас появятся позже. Чтобы определить эту разницу при оценке инвестиций, лучше всего подойдет показатель чистой приведенной стоимости (NVP).

Большинство людей знают, что деньги, которые у вас есть сейчас, более ценны, чем деньги, которые вы получите потом. Это связано с тем, что вы можете использовать их, чтобы заработать еще больше денег, управляя бизнесом, или купив что-то сейчас, чтобы продать это позже, или просто вкладывая деньги банк и зарабатывая проценты.

Будущие деньги также менее ценны, потому что инфляция снижает их покупательную способность. Это называется временной стоимостью денег.

Но как именно можно сравнить текущую стоимость денег со стоимостью денег в будущем?

Именно для этого финансисты рассчитывают чистую приведенную стоимость.

Что такое чистая приведенная стоимость?

Чистая приведенная стоимость или NPV (от англ. ‘Net Present Value’) представляет собой текущую стоимость денежных потоков, с учетом требуемой нормы доходности вашего проекта, по сравнению с вашими первоначальными инвестициями.

На практике NPV — это метод оценки доходности инвестиций или рентабельности инвестиций для проекта или капитальных расходов. Рассматривая все будущие денежные потоки, которые вы ожидаете от инвестиций, и переводя эти потоки в сегодняшнюю стоимость, вы можете решить, выгоден ли проект.

См. также:

CFA — Чистая приведенная стоимость (NPV) и правило чистой приведенной стоимости.

Для чего обычно компании используют NPV?

Когда менеджеру нужно сравнивать проекты и решить, какие из них следует одобрить, у него обычно есть три инструмента:

внутренняя норма доходности (IRR),
срок окупаемости (PP или ‘payback period’) и
чистая приведенная стоимость (NPV).

Показатель чистой приведенной стоимости — это выбор большинства финансовых аналитиков. На это есть две причины.

Во-первых, NPV учитывает временную стоимость денег, т.е. переводит будущие денежные потоки в сегодняшние деньги.
Во-вторых, он дает конкретное число, которое менеджеры могут использовать, чтобы легко сравнить первоначальные денежные затраты с текущей денежной отдачей.

Показатель NPV намного превосходит метод окупаемости (PP), который также часто используется.

Привлекательность показателя PP заключается в том, что его легко вычислить и просто понять: когда вы вернете деньги, которые вы вложили? Но он не принимает во внимание то, что покупательная способность денег сегодня больше, чем покупательная способность той же суммы денег в будущем.

Это то, что делает NPV превосходным методом оценки инвестиций. К счастью, сегодня с помощью финансовых калькуляторов и электронных таблиц NPV почти так же легко вычислить, как и PP.

Менеджеры также используют NPV, чтобы решить, делать ли крупные закупки, например, оборудования или программного обеспечения. Он также используется в слияниях и поглощениях (хотя в этом сценарии NPV называется моделью дисконтированных денежных потоков).

Фактически, это модель, которую использует Уоррен Баффет для оценки компаний.

Каждый раз, когда компания использует сегодняшние деньги для получения будущей прибыли, можно смело применять NPV.

5 } \)

То есть, вы рассчитываете этот показатель для каждого из этих 5 лет, а затем суммируете полученный результаты за каждый год. Это и будет текущая стоимость всех ваших прогнозируемых доходов. Затем вы вычитаете свои первоначальные инвестиции из этого числа, чтобы получить NPV.

Если NPV отрицательный, то проект нерентабелен.

В конечном итоге это приведет к утечке денежных средств из бизнеса. Однако, если показатель положительный, проект можно принять. Чем больше положительное число, тем больше выгода для компании.

Теперь вам будет интересно побольше узнать о ставке дисконтирования.

Ставка дисконтирования (от англ. ‘discount rate’) специфична для компании, поскольку она связана с тем, как компания ведет свою основную деятельность. Это норма прибыли, которую ожидают инвесторы от компании, или стоимость заимствования денег.

Если акционеры ожидают 12-процентного дохода, то это и есть ставка дисконтирования, которую компания будет использовать для расчета NPV. Если фирма выплачивает 4% по ее долгу, то она может использовать эту цифру в качестве ставки дисконтирования. Как правило, эту ставку определяет финансовый директор и его служба.

Каковы распространенные ошибки, которые делают люди при расчете NPV?

Есть две вещи, о которых следует знать при использовании NPV.

Во-первых, этот показатель трудно объяснить другим, то есть нефинансовым специалистам.

Дисконтированная стоимость будущих денежных потоков — это не та фраза, которую можно легко удалить из нефинансового языка.

Тем не менее, этот показатель стоит лишних усилий, чтобы объяснить его. Любая инвестиция, которая проходит тест NPV, увеличит акционерную стоимость, а любые инвестиции, которые не прошли этот тест, (если они будут осуществлены), непременно повредят компании и ее акционерам.

Второе, о чем должны помнить менеджеры, заключается в том, что расчет NPV основан на нескольких предположениях и оценках, а это значит, что он может быть субъективен и подвержен ошибкам. Вы можете уменьшить риски, дважды проверив свои оценки и сделав анализ чувствительности после того, как сделали свой первоначальный расчет.

Есть три узких места, где вы можете сделать ошибочные оценки, которые резко повлияют на конечные результаты вашего расчета.

Первоначальные инвестиции.
Знаете ли вы, сколько проект или расходы будут стоить? Если вы покупаете оборудование, имеющее фиксированную цену, то риска нет.
Но если вы обновляете свою ИТ-систему и планируете затраты на персонал в зависимости от сроков и этапов проекта, а также собираетесь делать предполагаемые закупки, суммы могут быть достаточно условными.

Риски, связанные со ставкой дисконтирования.
Вы используете сегодняшнюю ставку и применяете ее к будущим доходам, поэтому есть вероятность, что в третьем году проекта процентные ставки будут увеличиваться, а стоимость ваших средств повысится.
Это будет означать, что ваши доходы за этот год будут менее ценными, чем вы изначально думали.
Прогнозируемые результаты вашего проекта.
Именно здесь финансовые аналитики часто ошибаются в оценке. Вы должны быть относительно уверены в прогнозируемых результатах вашего проекта.
Эти прогнозы, как правило, оптимистичны, потому что люди ХОТЯТ сделать проект или ХОТЯТ купить оборудование.

Темы:

финансовый менеджмент

IRR

Другие публикации по этой теме:

Как рассчитать чистую текущую стоимость (NPV)

Чистая приведенная стоимость (NPV) — это метод, используемый для определения текущей стоимости всех будущих денежных потоков, генерируемых проектом, включая первоначальные капиталовложения. Он широко используется при бюджетировании капиталовложений, чтобы определить, какие проекты могут принести наибольшую прибыль.

Формула чистой приведенной стоимости варьируется в зависимости от количества и постоянства будущих денежных потоков.

Ключевые выводы

Чистая приведенная стоимость (NPV) используется для расчета сегодняшней стоимости будущего потока платежей.
NPV используется при составлении бюджета капиталовложений для сравнения того, приведут ли сегодняшние инвестиции к положительному денежному потоку в будущем.
Если чистая приведенная стоимость проекта или инвестиции положительна, это означает, что дисконтированная приведенная стоимость всех будущих денежных потоков, связанных с этим проектом или инвестицией, будет положительной и, следовательно, привлекательной.
Для расчета чистой приведенной стоимости необходимо оценить будущие денежные потоки для каждого периода и определить правильную ставку дисконтирования.
Чистая приведенная стоимость полезна для выявления прибыльных проектов, но неэффективна при сравнении проектов разного размера.

Нажмите «Играть», чтобы узнать формулу чистой приведенной стоимости

Что такое чистая приведенная стоимость?

Чистая приведенная стоимость — это метод анализа бюджета капиталовложений, используемый для определения того, будет ли долгосрочный проект прибыльным. Суть формулы NPV заключается в сравнении первоначальных инвестиций с будущими денежными потоками проекта.

Важным аспектом формулы NPV является рассмотрение того, что 1 доллар сегодня не стоит того же, что и 1 доллар завтра. Поскольку сегодняшние деньги можно использовать для получения дохода в будущем, количество денег сегодня стоит больше, чем такое же количество денег в будущем (при условии, что ожидается положительный доход).

В общем, формула NPV стремится привести все будущие значения денежных потоков к тому, что каждый денежный поток стоит сегодня. Затем формула NPV сравнивает стоимость этих притоков денежных средств с первоначальными инвестициями или оттоком денежных средств. Если чистая приведенная стоимость проекта положительна (дисконтированный будущий денежный поток больше, чем первоначальные инвестиции), ожидается, что проект будет прибыльным. Если чистая приведенная стоимость отрицательная, первоначальные инвестиции превышают будущие денежные потоки.

NPV Формула

9t} — \text{первоначальные инвестиции} \\ &\textbf{где:}\\ &i=\text{Требуемая доходность или ставка дисконтирования}\\ &t=\text{Количество периодов времени}\\ \end{выровнено} NPV = (1 + i) tДенежный поток – первоначальные инвестиции, где: i = требуемая доходность или коэффициент дисконтирования, t=количество периодов времени

Если анализировать долгосрочный проект с несколькими денежными потоками, то формула для NPV проекта выглядит следующим образом:

Н п В знак равно ∑ т знак равно 0 н р т ( 1 + я ) т куда: р т знак равно чистый приток-отток денежных средств за один период т я знак равно ставка дисконтирования или доход, который можно было бы получить при альтернативных инвестициях т знак равно количество периодов времени \begin{align} &NPV = \sum_{t = 0}^n \frac{R_t}{(1 + i)^t}\\ &\textbf{где:}\\ &R_t=\text{чистый приток денежных средств- оттоки в течение одного периода }t\\ &i=\text{ставка дисконтирования или доход, который можно было бы получить при альтернативных инвестициях}\\ &t=\text{количество периодов времени}\\ \end{выровнено} NPV=t=0∑n(1+i)tRtгде:Rt=чистый приток-отток денежных средств в течение одного периода ti=ставка дисконтирования или доход, который можно получить в альтернативных инвестицияхt=количество периодов времени

Если вы не знакомы с нотацией суммирования, вот более простой способ запомнить концепцию NPV:

Н п В знак равно Сегодняшнее значение ожидаемых денежных потоков − Сегодняшняя стоимость вложенных денежных средств NPV = \text{Сегодняшняя стоимость ожидаемых денежных потоков} — \text{Сегодняшняя стоимость вложенных денежных средств} NPV = сегодняшняя стоимость ожидаемых денежных потоков — сегодняшняя стоимость вложенных денежных средств.

Как рассчитать чистую приведенную стоимость с помощью Excel

В Excel есть функция NPV, которую можно использовать для простого расчета чистой приведенной стоимости ряда денежных потоков. Функция NPV в Excel — это просто NPV, и полное требование к формуле:

= NPV (ставка дисконтирования, будущий денежный поток) + первоначальные инвестиции

Пример NPV, Excel.

В приведенном выше примере формула, введенная в серую ячейку NPV, выглядит следующим образом:

= NPV (зеленая ячейка, желтые ячейки) + синяя ячейка

= NPV (C3, C6:C10) + C5

Ряд будущих денежных потоков может чередоваться между положительной и отрицательной доходностью. После первоначального оттока денежных средств компании может потребоваться ремонт оборудования, уплата налогов на землю или расходы на продажу определенного количества капитальных проектов.

Анализ формулы NPV

Формула NPV состоит из нескольких важных частей. Хотя формула может быть разной для разных типов потоков денежных средств, эти четыре компонента обычно имеют жизненно важное значение при расчете чистой приведенной стоимости.

Первоначальные инвестиции

При анализе NPV ряд денежных потоков обычно начинается с первоначальных инвестиций. Этот отток денежных средств представляет собой отрицательный отток денежных средств, который будет использоваться для сравнения с (надеюсь) положительным денежным потоком в будущем. Также принято считать, что инвестиции будут осуществлены в период 0 (начальный период до реализации инвестиций).

Например, представьте себе авансовые инвестиции в размере 100 000 долларов США в новое оборудование, которое повысит эффективность операций в будущем и обеспечит более эффективные методы производства. В этом примере формула NPV будет содержать отток денежных средств в размере 100 000 долларов США для представления первоначальных расходов.

Будущий денежный поток

Предпосылка NPV сосредоточена вокруг того, каким будет будущий денежный поток. Предполагается, что после первоначальных инвестиций инвестиции принесут положительный денежный поток в будущем. Этот денежный поток может возникнуть один раз в будущем, несколько раз в будущем для разных сумм или несколько раз в будущем для постоянного денежного потока.

В приведенном выше примере можно ожидать, что инвестиции в размере 100 000 долларов США принесут экономию средств в размере 25 000 долларов США в год в течение следующих пяти лет. В этом примере формула NPV будет содержать положительный денежный поток в размере 25 000 долларов США между периодами с 1 по 5.

Процентная ставка

Процентная ставка в формуле NPV также называется ставкой дисконтирования. Этот курс используется для определения того, сколько долларов в будущем стоит сегодня. Компания устанавливает эту ставку внутри компании, и компании часто используют стоимость капитала для установления этой ставки. Например, если выпуск дополнительного долга стоит 4% или акционеры ожидают дивиденды в размере 6%, компания может выбрать любую из этих ставок.

В нашем примере с машинами компания может ожидать, что ее стоимость капитала составит 5%. Таким образом, каждый денежный поток будет дисконтирован с использованием ставки 5%, хотя к каждому разному году денежного потока будут применяться разные скидки.

Период времени

Хотя это уже упоминалось ранее, подразумевается, что для инвестиций необходимо учитывать период времени. Компания может сделать разовые авансовые инвестиции; тем не менее, он может ожидать выгоды от денежных потоков в течение десятилетий в будущем. Если компания ожидает единовременный денежный поток в будущем, она должна определить период времени, когда они ожидают возврата.

Например, представьте, что компания покупает землю за 1 000 000 долларов. Он может либо использовать землю для операций, либо планирует продать ее за 1 500 000 долларов через пять лет. После выбора ставки дисконтирования 1,5 миллиона долларов следует дисконтировать, используя пять лет в качестве периода, чтобы лучше понять разницу между первоначальными инвестициями и дисконтированным будущим денежным потоком.

Аналог NPV называется внутренней нормой доходности (IRR). 3} — \$1000 \\ &= \$355,23\\ \end{выровнено} NPV=(1+0,08)1500$+(1+0,08)2300$+(1+0,08)3800$−1000$=355,23$

Требуемая норма доходности используется в качестве ставки дисконтирования для будущих денежных потоков для учета временной стоимости денег. Доллар сегодня стоит больше, чем доллар завтра, потому что доллар можно использовать для получения дохода. Следовательно, при расчете текущей стоимости будущих доходов денежные потоки, которые будут получены в будущем, должны быть уменьшены с учетом задержки.

NPV используется при составлении бюджета капиталовложений для сравнения проектов на основе их ожидаемой доходности, требуемых инвестиций и ожидаемого дохода с течением времени. Как правило, реализуются проекты с самой высокой чистой приведенной стоимостью.

Например, рассмотрим два потенциальных проекта для компании ABC.

Проект X требует первоначальных инвестиций в размере 35 000 долларов США, но ожидается, что он принесет доход в размере 10 000 долларов США, 27 000 долларов США и 19 000 долларов США в течение первого, второго и третьего года соответственно. Целевая норма прибыли – 12 %. Поскольку денежные потоки неравномерны, формула NPV разбивается на отдельные денежные потоки.

Н п В проекта − Икс знак равно $ 10 , 000 ( 1 + 0,12 ) 1 + $ 27 , 000 ( 1 + 0,12 ) 2 + $ 193} — \$35,000 \\ &= \$8,977\\ \end{выровнено} NPV проекта — X = (1 + 0,12)1 10 000 долларов США + (1+0,12)2 27 000 долларов США + (1+0,12)3 19 000 долларов – 35 000 долларов = 8 977 долларов США

Проект Y также требует первоначальных инвестиций в размере 35 000 долларов США и будет приносить 27 000 долларов США в год в течение двух лет. Целевая ставка остается на уровне 12%. Поскольку каждый период приносит одинаковые доходы, можно использовать первую приведенную выше формулу:

Н п В проекта − Д знак равно $ 27 , 000 ( 1 + 0,12 ) 1 + $ 27 , 000 ( 1 + 0,12 ) 2 − $ 35 , 000 знак равно $ 10 , 631 \begin{align} NPV \text{ проекта} — Y &= \frac{\$27,000}{(1 + 0,12)^1} + \frac{\$27,000}{(1+0,12)^2} — \$35,000 \\ &= \$10 631\\ \end{выровнено} NPV проекта – Y=(1+0,12)1 27 000 долларов США+ (1+0,12)2 27 000 долларов – 35 000 долларов = 10 631 долларов США

Оба проекта требуют одинаковых первоначальных инвестиций, но проект X приносит больший общий доход, чем проект Y. Однако проект Y имеет более высокую чистую приведенную стоимость, поскольку доход генерируется быстрее (это означает, что ставка дисконтирования оказывает меньшее влияние).

Преимущества формулы NPV

Формула NPV использует временную стоимость денег; По сравнению с другими инструментами анализа капиталовложений формула NPV дисконтирует денежный поток и анализирует прибыльность на основе времени возникновения денежного потока. Формула NPV также учитывает удельную стоимость капитала компании через ставку дисконтирования.

Дисконтируя денежный поток, формула NPV естественным образом учитывает долгосрочную подверженность риску. Самые дальние оценки в будущем дисконтируются наиболее сильно, учитывая, что эти денежные потоки часто имеют наибольшую неопределенность.

Формула NPV часто дает легко интерпретируемый расчет. Если результат положительный, то проект прибыльный. Если результат отрицательный, проект убыточен. В отличие от формулы IRR, которая дает процент, который необходимо сравнить с эталоном, NPV дает ценность сама по себе.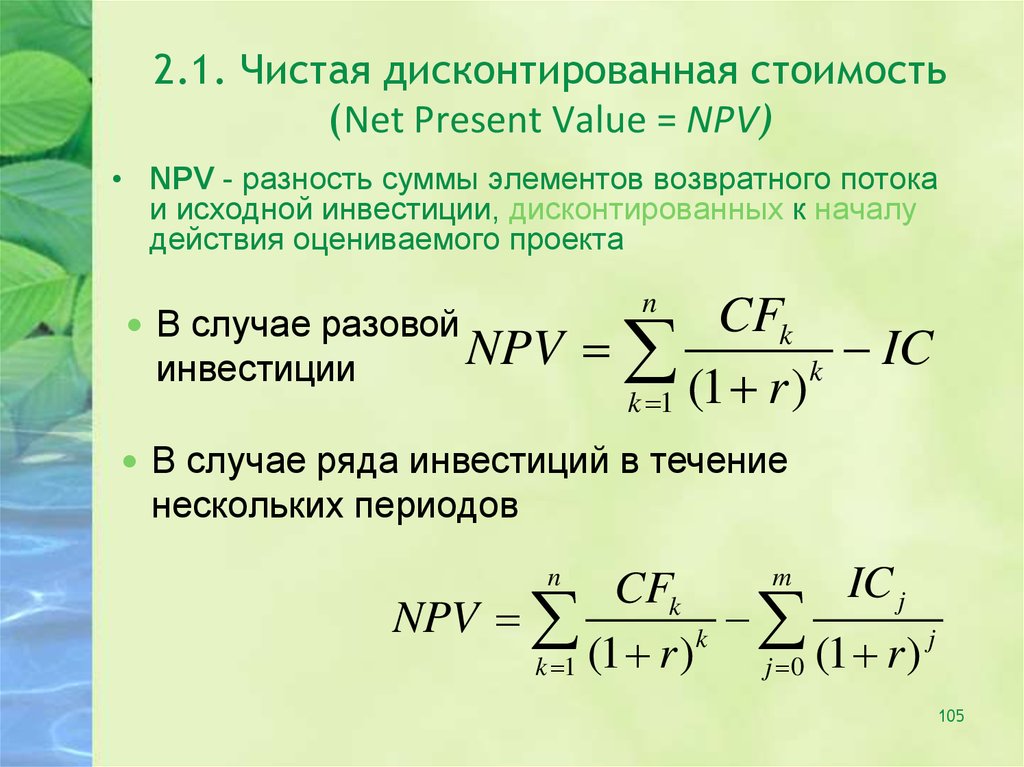

Ограничения формулы NPV

Как и другие финансовые формулы, используемые для стратегического планирования, формула чистой приведенной стоимости ценна ровно настолько, насколько ценны исходные данные. Формула чистой приведенной стоимости в значительной степени зависит от качества предоставленной информации, даже несмотря на то, что оценки могут быть рассчитаны на десятилетия вперед.

Формула NPV дает результат в долларах, который, хотя его легко интерпретировать, может не отражать всей картины. Рассмотрим следующие два варианта инвестирования: вариант А с чистой приведенной стоимостью 100 000 долларов или вариант Б с чистой приведенной стоимостью 1000 долларов.

Формула для NPV не различает размер проекта и не дает преимуществ для более высокой рентабельности инвестиций. Вариант A может потребовать первоначальных инвестиций в размере 1 миллиона долларов, а вариант B может потребовать первоначальных инвестиций в размере 10 долларов. Хотя формула NPV говорит вам, за какой проект вы можете заработать больше, она не говорит вам, какие инвестиции наиболее эффективны с точки зрения стартового капитала.

Формула NPV

Плюсы

Учитывает временную стоимость денег
Включает дисконтированный денежный поток с использованием стоимости капитала компании
Возвращает одно значение в долларах, которое относительно легко интерпретировать
Может быть легко вычислить при использовании электронных таблиц или финансовых калькуляторов

Минусы

В значительной степени зависит от исходных данных, оценок и долгосрочных прогнозов
Не различает размер проекта или рентабельность инвестиций
Может оказаться сложным и трудным для расчета вручную, особенно для проектов с многолетним денежным потоком
Основан на количественных данных и не учитывает нефинансовые показатели

Как рассчитывается чистая приведенная стоимость?

Чистая приведенная стоимость рассчитывается на основе приведенной стоимости всех денежных потоков в течение срока действия проекта. Затем текущая стоимость денежных потоков вычитается из первоначальных инвестиций. Если разница положительна (больше 0), проект будет прибыльным.

Для чего используется чистая приведенная стоимость (NPV)?

Чистая приведенная стоимость (NPV) используется при составлении бюджета капиталовложений для определения того, будет ли проект прибыльным, или для оценки различных проектов и определения того, какой из них будет наиболее прибыльным.

В чем основное преимущество NPV перед альтернативным методом, таким как период окупаемости?

Основное преимущество метода NPV заключается в том, что он учитывает временную стоимость денег путем дисконтирования будущих денежных потоков по соответствующей ставке дисконтирования, основанной на стоимости капитала компании и риске проекта. Период окупаемости оценивает, сколько времени потребуется проекту, чтобы генерировать денежные потоки, достаточные для погашения его первоначальных затрат на запуск, но он не учитывает временную стоимость денег и общую прибыльность проекта, как это делает NPV.

Каковы основные недостатки NPV?

Чистая приведенная стоимость требует точных допущений для ряда переменных, таких как первоначальные затраты и будущие денежные потоки, и, что наиболее важно, ставка дисконтирования или стоимость капитала. Поскольку небольшие изменения в ставке дисконтирования могут привести к значительным колебаниям дисконтированной стоимости будущих денежных потоков, неточные ставки дисконтирования могут привести к неправильной чистой приведенной стоимости и, следовательно, к ошибочному решению о рентабельности и жизнеспособности проекта.

Еще одним недостатком NPV является то, что его нельзя использовать для сравнения проектов разного размера, так как результат метода NPV выражается в долларах. Таким образом, проект стоимостью 10 миллионов долларов, вероятно, может иметь более высокую чистую приведенную стоимость, чем проект стоимостью 1 миллион долларов в долларовом выражении, но последний может быть гораздо более прибыльным в процентном отношении, если не считать того, что ему требуется только одна десятая часть капитала. Таким образом, эти два проекта нельзя сравнивать с использованием чистой приведенной стоимости, поскольку они имеют очень разные размеры.

Что означает отрицательное число NPV?

Отрицательное число NPV означает, что проект будет убыточным, поскольку первоначальные затраты на запуск превысят дисконтированную стоимость чистых будущих денежных потоков.

Практический результат

Чистая приведенная стоимость (NPV) дисконтирует все будущие денежные потоки от проекта и вычитает требуемые инвестиции. Анализ используется при составлении бюджета капиталовложений, чтобы определить, следует ли осуществлять проект по сравнению с альтернативным использованием капитала или другими проектами.

NPV Примеры | Шаг за шагом Примеры чистой приведенной стоимости

Чистая приведенная стоимость (NPV) относится к долларовой стоимости, полученной путем вычитания приведенной стоимости всех оттоков денежных средств компании из приведенной стоимости всех притоков денежных средств, пример которой включает Дело компании A ltd. где приведенная стоимость всех оттоков денежных средств составляет 100 000 долларов США, а приведенная стоимость всех притоков денежных средств составляет 120 000 долларов США, поэтому чистая приведенная стоимость будет равна 20 000 долларов США (120 000 долларов США – 100 000 долларов США)

Следующие примеры NPV (чистая приведенная стоимость) дают представление о наиболее распространенных инвестиционных решениях. Невозможно предоставить полный набор примеров, охватывающих все варианты в каждой ситуации, поскольку существуют тысячи таких проектов с анализом чистой приведенной стоимости. В каждом примере NPV указывается тема, соответствующие причины и дополнительные комментарии по мере необходимости.

Чистая приведенная стоимость — это разница между приведенной стоимостью будущих притоков денежных средств и приведенной стоимостью оттоков денежных средств за определенный период времени. NPV широко используется в составлении бюджета капиталовложений. Составление бюджета капиталовложений — это процесс планирования долгосрочных инвестиций, который определяет, будут ли проекты плодотворными для бизнеса и обеспечат ли они требуемую прибыль в будущем или нет. Это важно, потому что капитальные затраты требуют значительного количества средств. Читать дальше и знать рентабельность проекта.

Если чистая текущая стоимость положительна, проект следует принять. Это указывает на то, что доход от проекта превышает сумму, вложенную в проект, поэтому проект следует принять.
Если Чистая текущая стоимость отрицательная, то это указывает на то, что проект, в который мы вложили деньги, не обеспечивает положительной доходности, поэтому проект следует отклонить.

Математически NPV FormulaNPV FormulaNet Текущая стоимость (NPV) оценивает прибыльность проекта и представляет собой разницу между приведенной стоимостью притока денежных средств и приведенной стоимостью оттока денежных средств за период времени проекта. Если разница положительна, проект прибыльный; в противном случае это не так.Читать далее представлен как,

NPV = Денежные потоки /(1-i) ^t – Первоначальные инвестиции

Где

i означает требуемую норму прибыли, требуемую норму прибыли, требуемую норму прибыли (RRR), также известную как пороговая ставка, минимальная сумма капитала или доход, который инвестор ожидает получить от инвестиций. Он определяется по формуле Требуемая норма доходности = (Ожидаемая выплата дивидендов/Существующая цена акций) + Темп роста дивидендовЧитать далее или Ставка дисконтирования
t означает время или количество периодов

Соглашение о таблице

Примеры NPV (чистое приведенное значение)
- Примеры чистого приведенного значения (NPV)
  - Пример № 1
  - Пример № 2
  - Пример № 3
  - Пример #40010
- Рекомендуемые статьи

Примеры чистой приведенной стоимости (NPV)

Давайте рассмотрим несколько простых и сложных примеров чистой приведенной стоимости, чтобы лучше понять ее.

Пример №1

Компания A ltd хотела узнать чистую приведенную стоимость денежного потока, если они инвестируют 100 000 сегодня. И их первоначальные инвестиции в проект составляют 80000 на 3 года, и они ожидают доходность 10% в год. Из приведенной выше доступной информации рассчитайте NPV. 93-80000

NPV = 57174,21

Итак, в этом примере NPV положительна, поэтому мы можем принять проект.

Пример #2

В примере 2 ^и мы возьмем пример WACC (средневзвешенная стоимость капитала) для расчета NPV, потому что в WACC мы учитываем вес капитала и долга, а также стоимость собственного капитала и долга. Расчет чистой приведенной стоимости.

Решение:

Компания XYZ Ltd предоставляет следующую информацию о своем проекте за 10 лет.

Свободный денежный поток в фирмуСвободный денежный поток в фирмуFCFF (Свободный денежный поток в фирму), или неравномерный денежный поток, представляет собой денежные средства, остающиеся после выплаты амортизации, налогов и других инвестиционных затрат из выручки. Он представляет собой сумму денежного потока, доступного всем держателям финансирования – держателям долговых обязательств, держателям акций, держателям привилегированных акций или держателям облигаций. Подробнее см. ниже за определенный период времени. И + [Стоимость долга * % долга * (1-налоговая ставка)]” url=”https://www.wallstreetmojo.com/weighted-average-cost-capital-wacc/”]WACC”WACC””The составляет 15 %

Расчет NPV можно выполнить следующим образом:

NPV = 1104,55

В этом примере также чистая текущая стоимость положительна, поэтому мы можем или должны принять проект

Maruti занимается производством автомобилей и вспомогательного оборудования, и они хотят начать свой дочерний бизнес в качестве плана расширения по сборке автозапчастей, поэтому они предоставили приведенную ниже информацию для расчета чистой приведенной стоимости. Они хотят знать, будет ли этот проект осуществимым или нет.

Стоимость капитала — 35%
Стоимость долга — 15%
Вес акционера — 20%
Вес долга — 80%

. 32%

Cash flow is given below for 7 year
2010= -12000
2011=10000
2012=11000
2013=12000
2014=13000
2015=14000
2016=15000

Найдите NPV с помощью WACC.

Решение:

Расчет WACC можно выполнить следующим образом. , акционеров и владельцев привилегированных акций. Формула WACC = [Стоимость собственного капитала * % собственного капитала] + [Стоимость долга * % долга * (1-ставка налога)]подробнее = We*Ce+Wd*Cd*(1-ставка налога)

= 20*35+80*15*(1-32)

WACC = 15,16%

Расчет NPV можно сделать следующим образом,

NPV = 29151,0 NPV = 29151,0 9 . Например, мы получаем положительную чистую текущую стоимость будущих денежных потоков, поэтому и в этом примере мы примем проект.

Пример #4

Toyota хочет построить один новый завод для расширения текущего бизнеса, поэтому они хотят проверить осуществимость проекта. Toyota предоставила следующую информацию о денежных потоках и WACC. Движение денежных средств за период выглядит следующим образом.

2008 = -4000
2009 = -5000
2010 = 6000
2011 = 7000
2012 = 9000
2013 = 1200

Решение:

Диссула. следует,

NPV = 12348,33

Чистая приведенная стоимость проекта: Чистая приведенная стоимость