Чистая текущая стоимость npv это: Чистая текущая стоимость (NPV)
Чистая приведенная стоимость, NPV — Альт-Инвест
Открыть эту статью в PDF
Показатель чистой приведенной стоимости (Net Present Value, NPV) — одно из базовых понятий как в оценке проектов и компаний, так и вообще в финансовой математике. Его применяют для самых разных целей во всех сферах финансов — от анализа инвестиций до организации учета.
Определение NPV
Если у нас есть прогнозируемый денежный поток в течение N лет и каждый год платежи (положительные или отрицательные) равны CFi, то сегодняшняя стоимость данного денежного потока может быть вычислена по формуле:
где d — ставка дисконтирования. В зависимости от применения показателя NPV ставку дисконтирования определяют по-разному, но практически всегда она равна требуемой доходности инвестиций (поэтому ставку дисконтирования часто обозначают буквой r — от слова return).
В этом варианте записи формулы первый платеж CFiбудет через год (поэтому суммирование начинается с 1). Нередко бывает и так, что анализируемый денежный поток начинается с первого инвестиционного платежа, который надо сделать сегодня. Тогда формулу NPV записывают как:
или в более общем виде начальные инвестиции вносятся в суммирование как CF0:
В отличие от чистой прибыли проекта или компании NPV учитывает не только затраты, отраженные в обычном финансовом учете, но и такой экономический фактор, как минимальная доходность используемого капитала. Поэтому прибыль, рассчитанную с использованием NPV, называют экономической прибылью.
Применение в оценке инвестиционных проектов
Для оценки привлекательности инвестиционного проекта дисконтируют свободный денежный поток и рассчитывают NPV.
Отрицательное значение NPV говорит о том, что проект не привлекателен.
Обычно при расчете NPV инвестиции не выделяют как отдельный денежный поток, они просто создают отрицательные денежные потоки в начале инвестиционного проекта. Для того, чтобы учесть инвестиции в качестве денежного потока для дисконтирования используют либо свободный денежный поток компании (FCFF), либо свободный денежный поток акционерного капитала (FCFE).
При дисконтировании денежного потока проекта важно использовать ставку дисконтирования, которая соответствует способу построения денежного потока. Для анализа FCFF применяют WACC, для анализа FCFE — ставку требуемой доходности на собственный капитал. Кроме того, если прогноз денежных потоков был построен с учетом инфляции (в номинальных ценах), применяют номинальную ставку дисконтирования, а если без учета инфляции (в реальных ценах), — реальную.
Связь NPV и оценки бизнеса
NPV всех доходов, которые ожидают получить от анализируемой компании, дает сегодняшнюю стоимость этой компании — в этом и заключается оценка бизнеса доходным подходом.
В качестве будущих доходов используют прогнозируемые денежные потоки бизнеса. Как и для инвестиционных проектов, можно сформировать либо денежные потоки для компании — FCFF, либо денежные потоки для собственного капитала — FCFE. Первый вариант даст оценку стоимости всего бизнеса, из нее надо вычесть долги. Второй вариант оценивает сразу именно стоимость акционерного капитала.
Дисконтирование на начало, конец и середину периода
Длительность периода планирования при расчете NPV часто равна году. Это довольно продолжительный период времени, и результаты анализа будут зависеть от того, какое предположение вы сделаете о распределении денежных потоков внутри года. Возможны три варианта:
- Денежные потоки приходятся на конец года. Значит платежи первого периода уже следует продисконтировать как отстоящие на один год от сегодняшнего дня. Так работает функция Excel ЧПС().
- Денежные потоки приходятся на начало года.
 Значит платежи первого периода не надо дисконтировать, или следует считать, что номер этого периода — 0, т. к. (1+d) в нулевой степени равно 1, что как раз обеспечивает отсутствие дисконтирования.
Подход, при котором денежные потоки приходятся на начало периода, удобен в оценке инвестиционных проектов, — такие проекты часто начинаются с крупных расходов, которые не надо дисконтировать.
Значит платежи первого периода не надо дисконтировать, или следует считать, что номер этого периода — 0, т. к. (1+d) в нулевой степени равно 1, что как раз обеспечивает отсутствие дисконтирования.
Подход, при котором денежные потоки приходятся на начало периода, удобен в оценке инвестиционных проектов, — такие проекты часто начинаются с крупных расходов, которые не надо дисконтировать. - Денежные потоки распределяются равномерно по периоду. Для того, чтобы отразить это предположение в расчетах, надо дисконтировать все платежи по середине периода, то есть использовать номера периодов
Шаг дисконтирования не равный году
Если длительность шага расчета для прогнозируемых доходов не равна году, то применение ставки дисконтирования требует дополнительного учета шага. (n / 12), и модель станет универсальной для любой длительности периодов.
(n / 12), и модель станет универсальной для любой длительности периодов.
Еще один способ учесть длительность периодов — использовать функцию Excel ЧИСТНЗ(). Это аналог простой функции ЧПС(), но он использует еще один параметр — даты каждого платежа. Если в модели подготовлена строка, которая содержит даты для каждого периода прогнозных платежей, то функция ЧИСТНЗ() самостоятельно определит длительность каждого периода и скорректирует ставку дисконтирования.
Такие статьи мы публикуем регулярно. Чтобы получать информацию о новых материалах, а также быть в курсе учебных программ, вы можете подписаться на новостную рассылку.Если вам необходимо отработать определенные навыки в области инвестиционного или финансового анализа и планирования, посмотрите программы наших семинаров.
Чистая текущая стоимость NPV (Net Present Value). Достоинства и недостатки использования
Автор Zorg На чтение 2 мин. Просмотров 1k. Опубликовано
Просмотров 1k. Опубликовано
Чистая текущая стоимость (NPV,
Для расчета NPV необходимо посчитать сумму всех денежных потоков и провести дисконтирование.
Формула расчета чистой текущей стоимости
где: CFt – денежные потоки; r – ставка дисконтирования; CF0 – первоначальные инвестиции (отрицательные).
Денежные потоки, которые в формуле, как привило, формируются за рассматриваемые периоды: год, квартал, месяц. В итоге денежный поток, например помесячный, будет равен всем денежным поступлениям за месяц.
CF=CF1+CF2 +… + CFn
Чистая текущая стоимость (NPV) позволяет сравнить различные инвестиционные проекты между собой. Положительное значение NPV говорит о том, что данное инвестиционное вложение эффективно и привлекательно. Если NPV<0, то доходы от инвестиций не могут покрыть риск по данному проекту. Чем выше значения чистой текущей стоимости, тем инвестиционно привлекательнее проект.
Положительное значение NPV говорит о том, что данное инвестиционное вложение эффективно и привлекательно. Если NPV<0, то доходы от инвестиций не могут покрыть риск по данному проекту. Чем выше значения чистой текущей стоимости, тем инвестиционно привлекательнее проект.
Для расчета ставки дисконтирования, как правило, берут безрисковую ставку вложения, например, в государственные ценные бумаги (ГКО, ОФЗ), дополняют ее компенсацией за риск (риск не реализации проекта). Так же ставка дисконтирования может быть определена рыночным путем по доходности на фондовом рынке для проекта с таким же уровнем риска.
Достоинства и недостатки показателя чистой текущей стоимости (NPV)
К достоинствам чистой текущей стоимости можно отнести:
- четкость показателя для управленческих решений при выборе объекта инвестирования;
- использование ставки дисконтирования отражает свойство стоимости денег к обесцениванию;
- ставка дисконтирования может включать дополнительные риски проекта.

К недостаткам чистой текущей стоимости можно отнести:
- сложность расчета ставки дисконтирования может исказить результаты оценки показателя NPV. Это характерно для сложных проектов, включающих множество рисков;
- сложность прогнозирования денежных потоков. Хоть денежные потоки предприятия определяются, но это только прогнозные значения, которые в процессе могут изменяться;
- не учет нематериальных преимуществ и ценностей предприятия.
Так как денежные потоки могут изменяться со временем и носят вероятностный характер, то используют имитационное моделирования с заданием возможных вероятностей получения того или иного денежного потока. Вероятности для каждого денежного потока определяются экспертно. Для решения недостатков чистой текущей стоимости (NPV) используют смешанный подход, где нематериальный капитал и будущие денежные потоки оцениваются экспертами или экспертной группой.
Автор: к.э.н. Жданов И.Ю.
Почта: vani_zh@pochta. ru
ru
Сайт: www.beintrend.ru
Чистая текущая стоимость (NPV) 2021
Поделиться видео // www. Investopedia. ком / условия / п / NPV. aspЧто такое «Чистая текущая стоимость — NPV»
Чистая приведенная стоимость (NPV) — это разница между текущей стоимостью притока денежных средств и текущей стоимостью оттока денежных средств. NPV используется в бюджетировании капитала для анализа рентабельности прогнозируемых инвестиций или проекта.
Ниже приведена формула для расчета NPV:
где
C t = чистый приток денежных средств за период t
C o = общие начальные инвестиционные затраты
r = ставка дисконтирования и
t = количество периодов времени
Положительная чистая текущая стоимость указывает, что прогнозируемая прибыль от проекта или инвестиций (в текущих долларах) превышает ожидаемые затраты (также в текущих долларах). Как правило, инвестиции с положительной NPV будут прибыльными, а одна с отрицательной NPV приведет к чистым убыткам. Эта концепция является основанием для правила чистой текущей стоимости, которое диктует, что единственными инвестициями, которые должны быть сделаны, являются те, у которых есть положительные значения NPV.
Эта концепция является основанием для правила чистой текущей стоимости, которое диктует, что единственными инвестициями, которые должны быть сделаны, являются те, у которых есть положительные значения NPV.
Когда эти инвестиции являются приобретением или слиянием, можно также использовать показатель дисконтированного денежного потока (DCF).
Помимо самой формулы, чистая приведенная стоимость часто может рассчитываться с использованием таблиц, таблиц, таких как Microsoft Excel или собственного калькулятора NPV от Investopedia.
ВЫКЛЮЧЕНИЕ «Чистая приведенная стоимость — NPV»
Определение стоимости проекта является сложной задачей, поскольку существуют различные способы измерения стоимости будущих денежных потоков. Из-за временной стоимости денег (ТВМ) деньги в настоящем в будущем будут стоить больше той же суммы. Это связано как с доходами, которые потенциально могут быть сделаны с использованием денег в течение промежуточного времени и из-за инфляции. Другими словами, доллар, заработанный в будущем, не будет стоить столько, сколько заработал в настоящем.
Элемент учетной ставки формулы NPV является способом учета этого. Компании часто могут иметь разные способы определения ставки дисконтирования. Общие методы определения ставки дисконтирования включают использование ожидаемого возврата других вариантов инвестиций с аналогичным уровнем риска (ожидаются инвесторы с доходностью) или затраты, связанные с заимствованием денег, необходимых для финансирования проекта.
Например, если бизнес розничной одежды хочет приобрести существующий магазин, он сначала оценит будущие потоки денежных средств, которые будут хранить, и затем будет обесценивать эти денежные потоки (r) на одну единовременную сумму, $ 500 000. Если владелец магазина готов продать свой бизнес менее чем за 500 000 долларов США, покупка компании, скорее всего, согласится на это предложение, так как оно представляет собой положительную инвестицию NPV.Если владелец согласился продать магазин за 300 000 долларов США, то в течение расчетного инвестиционного периода инвестиции представляют собой чистую прибыль в размере 200 000 долларов США (500 000 долларов США — 300 000 долларов США). Это 200 000 долларов США или чистая прибыль от инвестиций называется внутренней стоимостью инвестиций. И наоборот, если владелец не будет продавать менее чем за 500 000 долларов США, покупатель не купит магазин, так как это приобретение будет представлять собой отрицательную NPV в то время и, следовательно, снизит общую стоимость более крупной швейной компании.
Это 200 000 долларов США или чистая прибыль от инвестиций называется внутренней стоимостью инвестиций. И наоборот, если владелец не будет продавать менее чем за 500 000 долларов США, покупатель не купит магазин, так как это приобретение будет представлять собой отрицательную NPV в то время и, следовательно, снизит общую стоимость более крупной швейной компании.
Давайте посмотрим, как этот пример вписывается в приведенную выше формулу. Суммарная текущая сумма $ 500 000 представляет собой часть формулы между знаком равенства и знаком минус. Сумма, которую оплачивает магазин розничной одежды для магазина, представляет собой C o . Вычтите C o от $ 500 000, чтобы получить NPV: если C o составляет менее $ 500 000, результат NPV положителен; если C o составляет более $ 500 000, NPV отрицательна и не является прибыльной инвестицией.
Недостатки и альтернативы
Одной из основных проблем с оценкой рентабельности инвестиций с NPV является то, что NPV в значительной степени опирается на несколько допущений и оценок, поэтому может быть существенное пространство для ошибок. Оценочные факторы включают инвестиционные затраты, учетную ставку и прогнозируемые доходы. Проект может часто требовать непредвиденных расходов для выхода из земли или может потребовать дополнительных расходов в конце проекта.
Оценочные факторы включают инвестиционные затраты, учетную ставку и прогнозируемые доходы. Проект может часто требовать непредвиденных расходов для выхода из земли или может потребовать дополнительных расходов в конце проекта.
Кроме того, ставки дисконтирования и оценки притока денежных средств не могут изначально учитывать риск, связанный с проектом, и могут предполагать максимальный возможный приток денежных средств в течение инвестиционного периода. Это может произойти как средство искусственного повышения доверия инвесторов. Таким образом, эти факторы, возможно, необходимо будет скорректировать с учетом непредвиденных затрат или потерь или чрезмерно оптимистичных прогнозов притока денежных средств.
Период окупаемости — это одна популярная метрика, которая часто используется в качестве альтернативы чистой приведенной стоимости. Это намного проще, чем NPV, в основном, измеряя время, требуемое после инвестиций, чтобы компенсировать первоначальные затраты на эти инвестиции. В отличие от NPV, период окупаемости (или «метод окупаемости») не учитывает временную стоимость денег. По этой причине периоды окупаемости, рассчитанные для более длительных инвестиций, имеют больший потенциал для неточностей, поскольку они охватывают больше времени, в течение которого может возникать инфляция, и косой прогнозируемый доход, а также реальный срок окупаемости.
В отличие от NPV, период окупаемости (или «метод окупаемости») не учитывает временную стоимость денег. По этой причине периоды окупаемости, рассчитанные для более длительных инвестиций, имеют больший потенциал для неточностей, поскольку они охватывают больше времени, в течение которого может возникать инфляция, и косой прогнозируемый доход, а также реальный срок окупаемости.
Кроме того, срок окупаемости строго ограничен количеством времени, требуемого для возврата первоначальных инвестиционных затрат. Таким образом, он также не учитывает прибыльность инвестиций после того, как эти инвестиции достигли конца периода окупаемости. Вполне возможно, что норма прибыли от инвестиций может впоследствии иметь резкое падение, резкое увеличение или что-то среднее между ними. Таким образом, сравнение периодов окупаемости инвестиций не обязательно даст точное представление о прибыльности этих инвестиций.
Внутренняя норма прибыли (IRR) — это еще одна метрика, обычно используемая в качестве альтернативы NPV. Расчеты IRR полагаются на ту же формулу, что и NPV, за исключением небольших корректировок. Расчеты IRR предполагают нейтральную NPV (значение нуля), а одно вместо этого решает для ставки дисконтирования. Ставка дисконтирования инвестиций, когда NPV равна нулю, является IRR инвестиций, в основном представляя прогнозируемые темпы роста для этих инвестиций. Поскольку IRR обязательно годовой — он относится к прогнозируемой доходности на ежегодной основе — это позволяет упростить сравнение широкого разнообразия типов и продолжительности инвестиций.
Расчеты IRR полагаются на ту же формулу, что и NPV, за исключением небольших корректировок. Расчеты IRR предполагают нейтральную NPV (значение нуля), а одно вместо этого решает для ставки дисконтирования. Ставка дисконтирования инвестиций, когда NPV равна нулю, является IRR инвестиций, в основном представляя прогнозируемые темпы роста для этих инвестиций. Поскольку IRR обязательно годовой — он относится к прогнозируемой доходности на ежегодной основе — это позволяет упростить сравнение широкого разнообразия типов и продолжительности инвестиций.
Например, IRR может использоваться для сравнения ожидаемой прибыльности трехлетних инвестиций с инвестициями в 10 лет, поскольку она выглядит как годовая цифра. Если оба имеют IRR 18%, то инвестиции в некоторых отношениях сопоставимы, несмотря на разницу в продолжительности. Тем не менее, то же самое не относится к чистой приведенной стоимости. В отличие от IRR, NPV существует как единое значение, использующее весь планируемый инвестиционный период. Если период инвестиций превышает один год, NPV не учитывает темпы прибыли, что позволяет легко сравнивать. Возвращаясь к предыдущему примеру, 10-летние инвестиции могут иметь более высокую NPV, чем 3-летние инвестиции, но это не обязательно полезная информация, так как первая более чем в три раза больше, чем последняя, и существует существенная объем инвестиционных возможностей в разнице между двумя инвестициями за 7 лет.
Если период инвестиций превышает один год, NPV не учитывает темпы прибыли, что позволяет легко сравнивать. Возвращаясь к предыдущему примеру, 10-летние инвестиции могут иметь более высокую NPV, чем 3-летние инвестиции, но это не обязательно полезная информация, так как первая более чем в три раза больше, чем последняя, и существует существенная объем инвестиционных возможностей в разнице между двумя инвестициями за 7 лет.
Заинтересованы в дополнительной информации о чистой приведенной стоимости? См .: Временная стоимость денег: определение будущего и наше введение в корпоративные методы оценки. Дополнительную информацию о взаимосвязи между NPV, IRR и связанными условиями см. В разделе нашего руководства по корпоративным финансам под названием «Чистая текущая стоимость и внутренняя норма прибыли».
что это такое и как рассчитать чистый дисконтированный доход (формула)
Показатель Net present value, или NPV инвестиционного проекта позволяет определить, какой доход получит инвестор в денежном выражении вследствие своих инвестиций. Другими словами, NPV проекта показывает размер финансовых поступлений как результата вложений в инвестиционный проект с учётом сопутствующих затрат, то есть – чистый дисконтированный доход. Что такое NPV на практике и как рассчитать чистый дисконтированный доход, станет понятно из приведённой ниже NPV-формулы и пояснений к ней.
Другими словами, NPV проекта показывает размер финансовых поступлений как результата вложений в инвестиционный проект с учётом сопутствующих затрат, то есть – чистый дисконтированный доход. Что такое NPV на практике и как рассчитать чистый дисконтированный доход, станет понятно из приведённой ниже NPV-формулы и пояснений к ней.
Содержание статьи
Понятие и содержание значения NPV
Прежде чем при переходе к теме NPV говорить, что это такое и как его рассчитать, надо понять значение фразы, из которой складывается аббревиатура. Для словосочетания «Net present value» в отечественной экономической и математической литературе можно найти несколько традиционных вариантов перевода:
- В первом варианте, характерном для математических учебников, NPV определяется как чистый дисконтированный доход (ЧДД).
- Второй вариант – чистая приведённая стоимость (ЧПС) – наряду с первым считается самым употребляемым.

- Третий вариант – чистый приведенный доход – совмещает в себе элементы первого и второго переводов.
- Четвёртый вариант перевода термина NPV, где PV – это «текущая стоимость», наименее распространён и широкого хождения не имеет.
Независимо от перевода, значение NPV остаётся неизменным, а термин этот означает, что
NPV – это такое чистое приведённое к текущему моменту значение стоимости. То есть, дисконтирование денежного потока как раз и рассматривается как процесс установления его (потока) стоимости посредством приведения стоимости совокупных выплат к определённому (текущему) моменту времени. Поэтому определение значения чистого дисконтированного дохода (NPV) становится, наряду с IRR, ещё одним способом оценить эффективность инвестиционных проектов заранее.
На уровне общего алгоритма, чтобы определит перспективность бизнес-проекта по данному показателю, нужно сделать следующие шаги:
- оценить движение денежных потоков – первоначальные вложения и ожидаемые поступления,
- установить стоимость капитала – посчитать ставку,
- дисконтировать входящие и выходящие денежные потоки по установленному показателю ставки,
- суммировать все дисконтированные потоки, что и даст величину NPV.

Если NPV-расчет демонстрирует величины больше нуля, значит, инвестиции прибыльны. Причём, чем больше число NPV, тем больше, при прочих равных, ожидаемое значение прибыли. Учитывая, что доход кредиторов обычно бывает фиксированным, всё, что проект принесет сверх него, принадлежит акционерам – с положительным NPV акционеры заработают. Обратная ситуация с NPV меньше нуля сулит инвесторам убытки.
Возможна ситуация, при которой чистый дисконтированный доход будет равен нулю. Это означает, что денежных потоков хватает на возмещение инвестированного капитала без прибыли. При одобрении проекта с NPV равным нулю, размер компания увеличится, но цена акций останется неизменной. Но инвестирование в такие проекты может быть связано с социальными или экологическими задачами инициаторов процесса, что делает возможным инвестирование в подобные проекты.
Формула NPV
Рассчитывают чистый дисконтированный доход по формуле расчета, которая в упрощённом виде выглядит как PV – ICo, где PV представляет собой текущие показатели денежного потока, а ICo – размер первоначальной инвестиции. В более сложном виде, где показан механизм дисконтирования, формула выглядит следующим образом:
В более сложном виде, где показан механизм дисконтирования, формула выглядит следующим образом:
NPV= — ICo + ∑nt=1 CFt / (1 + R)t
Здесь:
- NPV – чистый дисконтированный доход.
- CF – Cash Flow – денежный поток (инвестиционные платежи), а t рядом с показателем – время, в течение которого осуществляется денежный поток (например, годичный интервал).
- R – Rate – дисконт (ставка: коэффициент, который дисконтирует потоки).
- n – количество этапов реализации проекта, определяющее длительность его жизненного цикла (например, количество лет).
- ICo – Invested Capital – начальный инвестируемый капитал.
Таким образом, NPV рассчитывается как разность совокупных денежных потоков, актуализированных на определённый момент времени по факторам риска и первоначальной инвестиции, то есть, считается инвесторская прибыль как добавочная стоимость проекта.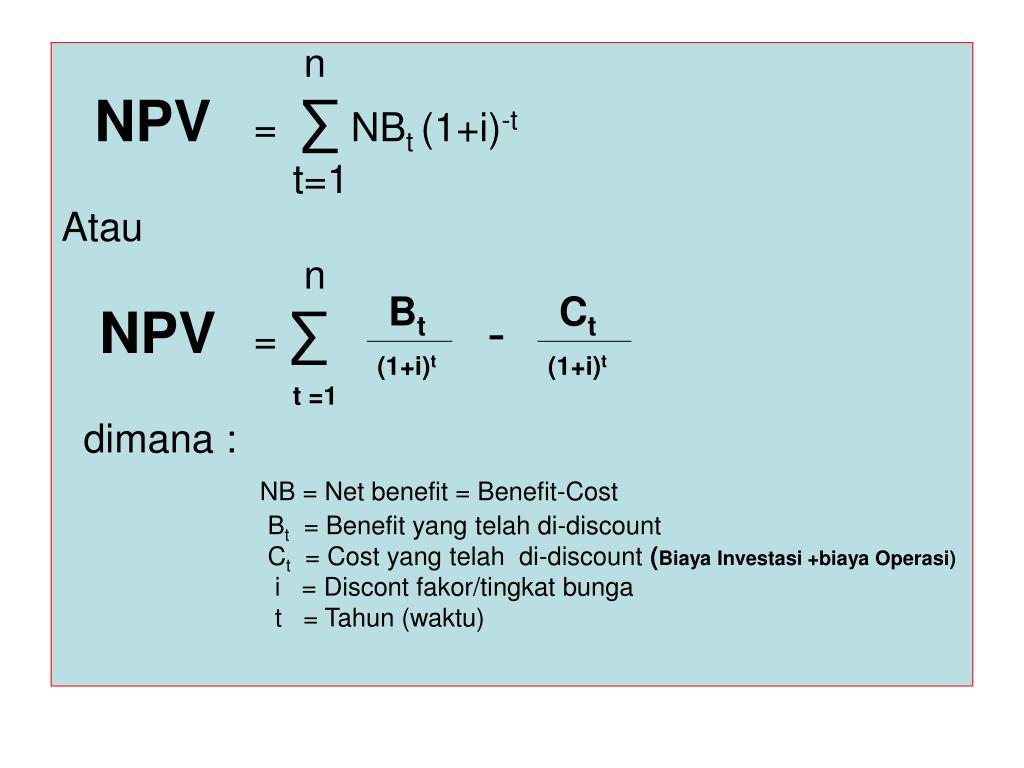
Поскольку для инвестора важно не только выгодное вложение, но и грамотное управление капиталом на протяжении продолжительного времени, данная формула может быть ещё расширена так, чтобы предусматривать не разовые, а дополнительные периодические вложения и коэффициент инфляции (i)
NPV= ∑nt=1 CFt / (1 + R)t — ∑mj =1 ICj / (1 + i)j
Пример расчёта NPV
Пример расчета для трёх условных проектов позволяет, как рассчитать NPV, так и определить, какой из проектов будет более привлекательным для инвестирования.
Согласно условиям примера:
- начальные инвестиции – ICo – в каждый из трёх проектов равны 400 у.е.,
- норма прибыли – ставка дисконтирования – составляет 13%,
- прибыль, которые могут приносить проекты (по годам), расписана в таблице на 5-летний срок.
Рассчитаем чистый дисконтированный доход, чтобы выбрать наиболее выгодный для инвестирования проект.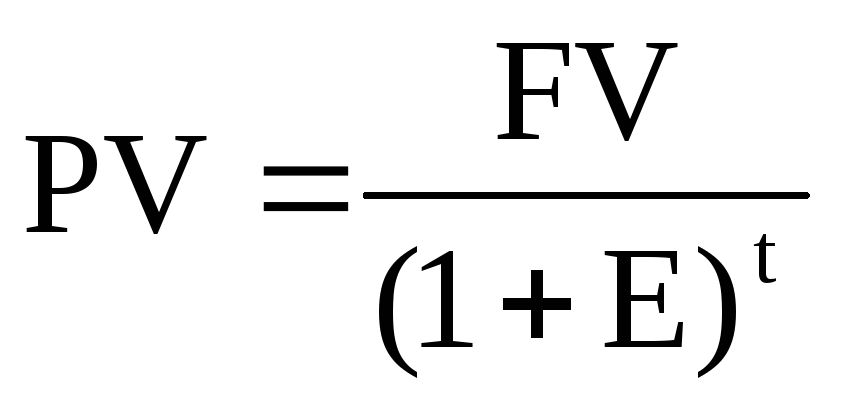 Фактор дисконтирования 1/(1 + R)t для интервала в один год будет t = 1: 1/(1+0,13)1 = 0,885. Если пересчитать NPV каждого сценария по годам с подстановкой в формулу определяющих значений, то получается, что для первого проекта NPV= 0,39, для второго – 10,41, для третьего – 7,18.
Фактор дисконтирования 1/(1 + R)t для интервала в один год будет t = 1: 1/(1+0,13)1 = 0,885. Если пересчитать NPV каждого сценария по годам с подстановкой в формулу определяющих значений, то получается, что для первого проекта NPV= 0,39, для второго – 10,41, для третьего – 7,18.
По этой формуле чистый приведённый доход выше всего у второго проекта, поэтому, если основываться только на параметре NPV, то он и будет самым привлекательным для инвестиций с точки зрения прибыли.
Однако сравниваемые проекты могут иметь разную продолжительность (жизненный цикл). Поэтому нередки ситуации, когда, например, при сравнении трёхлетнего и пятилетнего проектов NPV будет больше у пятилетнего, а среднее значение по годам – у трёхлетнего. Чтобы не возникло противоречий, рассчитываться в таких ситуациях должна ещё и среднегодовая норам доходности (IRR).
Кроме того, объём первоначальных инвестиций и ожидаемая прибыль известны не всегда, что создаёт сложности в применении расчётов.
Сложности применения расчётов
Как правило, в реальности считанные (подставляемые в формулу) переменные редко бывают точны. Главную сложность представляет определение двух параметров: оценки всех связанных с проектом денежных потоков и ставки дисконтирования.
CF– денежные потоки
Денежные потоки представляют собой:
- первоначальную инвестицию – стартовый отток средств,
- годовые притоки и оттоки средств, ожидаемые в последующие периоды.
В совокупности величина потока говорит о количестве денежных средств, которое есть в распоряжении предприятия или компании в текущий момент времени. Он же является показателем финансовой устойчивости компании. Для вычисления его значений надо из величины Cash Inflows (CI) – притока денежных средств – вычесть Cash Outflows (CO), отток:
CF = CI — CO
При прогнозировании потенциальных поступлений нужно определить характер и степень зависимости между влиянием факторов, которые формируют денежные поступления, и самим наполнением денежного потока. Процессуальная сложность большого комплексного проекта ещё и в объёме информации, которую необходимо учесть. Так в проекте, связанном с выпуском нового товара нужно будет спрогнозировать объём предполагаемых продаж в штуках, одновременно определив цену каждой проданной единицы товара. А в долгосрочном периоде, для того, чтобы это учесть, возможно, потребуется основываться в прогнозах на общем состоянии экономики, подвижности спроса в зависимости от потенциала развития конкурентов, на эффективность рекламных кампаний и массу других факторов.
Процессуальная сложность большого комплексного проекта ещё и в объёме информации, которую необходимо учесть. Так в проекте, связанном с выпуском нового товара нужно будет спрогнозировать объём предполагаемых продаж в штуках, одновременно определив цену каждой проданной единицы товара. А в долгосрочном периоде, для того, чтобы это учесть, возможно, потребуется основываться в прогнозах на общем состоянии экономики, подвижности спроса в зависимости от потенциала развития конкурентов, на эффективность рекламных кампаний и массу других факторов.
В части операционных процессов надо спрогнозировать расходы (платежи), что, в свою очередь, потребует оценки цен на сырьё, арендные ставки, коммунальные услуги, зарплаты, курсовые изменения на валютном рынке и другие факторы. Причём, если планируется многолетний проект, то и оценки следует делать на соответствующее количество лет вперёд.
Если же речь идёт о венчурном проекте, который ещё не имеет статистических данных по показателям производства, продаж и затрат, то тут прогнозирование денежного дохода осуществляется на основе экспертного подхода. Предполагается, что эксперты должны соотнести растущий проект с его отраслевыми аналогами и, вместе с потенциалом развития, оценить возможности денежных поступлений.
Предполагается, что эксперты должны соотнести растущий проект с его отраслевыми аналогами и, вместе с потенциалом развития, оценить возможности денежных поступлений.
R – ставка дисконтирования
Ставка дисконтирования – это своего рода альтернативная доходность, которую инвестор потенциально мог бы получить. Благодаря определению ставки дисконтирования производится оценка стоимости компании, что является одной из наиболее частых целей установления этого параметра.
Оценка производится на основе целого ряда методов, у каждого из которых есть свои преимущества и исходные данные, используемые при расчёте:
- Модель CAPM. Методика позволяет учитывать влияние рыночных рисков на величину ставки дисконтирования. Оценка производится на основе торгов биржи ММВБ, определяющих котировки обыкновенных акций. В своих преимуществах и выборе исходных данных метод схож на модель Фамы и Френча.
- Модель WACC.
 Преимущество модели в возможности принимать во внимание степень эффективности и собственного, и заёмного капиталов. Помимо котировок обыкновенных акций, во внимание принимаются процентные ставки по заёмному капиталу.
Преимущество модели в возможности принимать во внимание степень эффективности и собственного, и заёмного капиталов. Помимо котировок обыкновенных акций, во внимание принимаются процентные ставки по заёмному капиталу. - Модель Росса. Даёт возможность учитывать макро- и микрофакторы рынка, отраслевые особенности, определяющие ставку дисконтирования. В качестве исходных данных используется статистика Росстата по макроиндикаторам.
- Методы, основанные на рентабельности капитала, которые базируются на данных бухгалтерского баланса.
- Модель Гордона. По ней инвестор может просчитать дивидендную доходность, тоже опираясь на котировки обыкновенных акций, и также другие модели.
Изменение ставки дисконтирования и величины чистого приведённого дохода связаны между собой нелинейной зависимостью, которую просто можно отразить на графике. Отсюда следует правило для инвестора: при выборе проекта – объекта инвестиций – нужно сравнивать не только значения NPV, но также характер их изменения в зависимости от значений ставки. Вариабельность сценариев позволяет инвестору выбрать для вложений менее рискованный проект.
Вариабельность сценариев позволяет инвестору выбрать для вложений менее рискованный проект.
С 2012 года с подачи ЮНИДО расчет NPV входит в качестве элемента в расчёт индекса скорости удельного прироста стоимости, что считается оптимальным подходом при выборе лучшего инвестиционного решения. Способ оценки был предложен группой экономистов, возглавляемой А.Б. Коганом, в 2009 году. Он позволяет эффективно сравнивать альтернативы в ситуациях, где не удаётся провести сопоставление по единому критерию, и поэтому в основу сравнения положены разные параметры. Такие ситуации возникают, когда анализ инвестиционной привлекательности традиционными методами NPV и IRR не приводит к однозначным результатам или когда результаты методов противоречат друг другу.
Чистая приведенная стоимость (NPV) – Финансовая энциклопедия
Что такое Чистая приведенная стоимость (NPV)?
Чистая приведенная стоимость (NPV) – это разница между текущей стоимостью денежных поступлений и текущей стоимостью оттока денежных средств за период времени. NPV используется при составлении бюджета капиталовложений и инвестиционном планировании для анализа прибыльности планируемых инвестиций или проектов.
NPV используется при составлении бюджета капиталовложений и инвестиционном планировании для анализа прибыльности планируемых инвестиций или проектов.
Следующая формула используется для расчета NPV:
Если вы не знакомы с обозначением суммирования – вот более простой способ запомнить концепцию NPV:
NPVзнак равноТВЕСФ-ТВИСжчере:ТВЕСФзнак равноТодY’секпротивлуйоетчеехрестедсычелöже ТВИСзнак равноТодY’секпротивлуеоеянvéсектедр асекч \ begin {align} & \ textit {NPV} = \ text {TVECF} – \ text {TVIC} \\ & \ textbf {где:} \\ & \ text {TVECF} = \ text {Сегодняшняя сумма ожидаемых денежных средств потоки} \\ & \ text {TVIC} = \ text {Сегодняшняя стоимость вложенных денежных средств} \\ \ end {выровнено}Взаимодействие с другими людьмиЧПСзнак равноTVECF-TVICкуда:TVECFзнак равноСегодняшняя стоимость ожидаемых денежных потоковTVICзнак равноСегодняшняя стоимость вложенных денежных средствВзаимодействие с другими людьми
Положительная чистая приведенная стоимость указывает на то, что прогнозируемая прибыль, полученная от проекта или инвестиций – в текущих долларах – превышает ожидаемые затраты, также в настоящих долларах. Предполагается, что инвестиция с положительной NPV будет прибыльной, а инвестиция с отрицательной NPV приведет к чистому убытку. Эта концепция является основой правила чистой приведенной стоимости, согласно которому следует рассматривать только инвестиции с положительными значениями NPV.
Предполагается, что инвестиция с положительной NPV будет прибыльной, а инвестиция с отрицательной NPV приведет к чистому убытку. Эта концепция является основой правила чистой приведенной стоимости, согласно которому следует рассматривать только инвестиции с положительными значениями NPV.
Помимо самой формулы, чистую приведенную стоимость можно рассчитать с помощью таблиц, электронных таблиц или калькуляторов.
0:22
Как рассчитать чистую приведенную стоимость (NPV)
Деньги в настоящем стоят больше, чем такая же сумма в будущем, из-за инфляции и доходов от альтернативных инвестиций, которые можно было бы сделать в промежуточный период. Другими словами, доллар, заработанный в будущем, не будет стоить столько, сколько доллар, заработанный в настоящее время. Элемент ставки дисконтирования формулы NPV позволяет учесть это.
Например, предположим, что инвестор может выбрать платеж в размере 100 долларов сегодня или через год. Рациональный инвестор не захочет откладывать платеж. Однако что, если инвестор мог бы выбрать получение 100 долларов сегодня или 105 долларов в год? Если плательщик был надежным, эти дополнительные 5% могли стоить ожидания, но только в том случае, если не было ничего другого, что инвесторы могли бы сделать со 100 долларами, которые могли бы принести более 5%.
Однако что, если инвестор мог бы выбрать получение 100 долларов сегодня или 105 долларов в год? Если плательщик был надежным, эти дополнительные 5% могли стоить ожидания, но только в том случае, если не было ничего другого, что инвесторы могли бы сделать со 100 долларами, которые могли бы принести более 5%.
Инвестор может подождать год, чтобы заработать дополнительные 5%, но это может быть приемлемо не для всех инвесторов. В этом случае 5% – это ставка дисконтирования, которая будет варьироваться в зависимости от инвестора. Если бы инвестор знал, что он может заработать 8% от относительно безопасного вложения в течение следующего года, он не захотел бы откладывать выплату 5%. В этом случае ставка дисконтирования инвестора составляет 8%.
Компания может определить ставку дисконтирования, используя ожидаемую доходность других проектов с аналогичным уровнем риска или стоимость заимствования денег, необходимых для финансирования проекта. Например, компания может избежать проекта, который, как ожидается, будет приносить 10% в год, если финансирование проекта стоит 12%, или альтернативный проект, как ожидается, будет приносить 14% в год.
Представьте, что компания может инвестировать в оборудование, которое будет стоить 1 000 000 долларов и, как ожидается, будет приносить 25 000 долларов дохода в месяц в течение пяти лет. Компания имеет доступный капитал для приобретения оборудования и может в качестве альтернативы инвестировать его в фондовый рынок с ожидаемой доходностью 8% в год. Менеджеры считают, что покупка оборудования или инвестирование в фондовый рынок – аналогичные риски.
Шаг первый: чистая приведенная стоимость первоначальных инвестиций
Поскольку оборудование оплачивается авансом, это первый денежный поток, включенный в расчет. Нет истекшего времени, которое нужно учитывать, поэтому сегодняшний отток в размере 1000000 долларов не нужно сбрасывать со счетов.
Определите количество периодов (t)
Ожидается, что оборудование будет генерировать ежемесячный денежный поток и прослужит пять лет, что означает, что в расчет будет включено 60 денежных потоков и 60 периодов.
Определите ставку дисконтирования (i)
Ожидается, что альтернативные инвестиции принесут 8% годовых.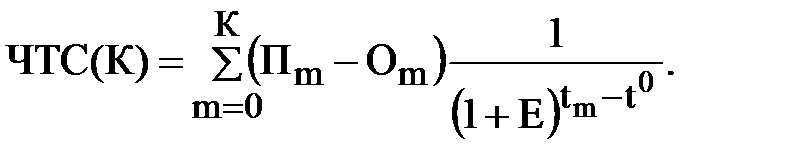 Однако, поскольку оборудование генерирует ежемесячный поток денежных средств, годовую ставку дисконтирования необходимо преобразовать в периодическую или ежемесячную. Используя следующую формулу, мы находим, что периодическая ставка составляет 0,64%.
Однако, поскольку оборудование генерирует ежемесячный поток денежных средств, годовую ставку дисконтирования необходимо преобразовать в периодическую или ежемесячную. Используя следующую формулу, мы находим, что периодическая ставка составляет 0,64%.
Шаг второй: чистая приведенная стоимость будущих денежных потоков
Предположим, что ежемесячные денежные потоки зарабатываются в конце месяца, а первый платеж поступает ровно через месяц после покупки оборудования. Это будущий платеж, поэтому его необходимо скорректировать с учетом временной стоимости денег. Инвестор может легко выполнить этот расчет с помощью электронной таблицы или калькулятора. Чтобы проиллюстрировать концепцию, первые пять платежей показаны в таблице ниже.
Полный расчет приведенной стоимости равен приведенной стоимости всех 60 будущих денежных потоков за вычетом инвестиций в размере 1 000 000 долларов США. Расчет мог бы быть более сложным, если бы предполагалось, что оборудование будет иметь какое-либо значение, оставшееся в конце его срока службы, но в этом примере предполагается, что оно бесполезно. {60}}NPVзнак равно-1доллар,000,000+∑t=160Взаимодействие с другими людьми(1+0.0064)60
{60}}NPVзнак равно-1доллар,000,000+∑t=160Взаимодействие с другими людьми(1+0.0064)60
Эту формулу можно упростить до следующего расчета:
В этом случае ЧПС положительна; оборудование следует покупать. Если приведенная стоимость этих денежных потоков была отрицательной, потому что ставка дисконтирования была больше, или чистые денежные потоки были меньше, инвестиций следовало бы избежать.
Недостатки чистой приведенной стоимости и альтернативы
Оценка прибыльности инвестиций с помощью NPV в значительной степени зависит от предположений и оценок, поэтому может существовать значительный простор для ошибок. Предполагаемые факторы включают инвестиционные затраты, ставку дисконтирования и прогнозируемую доходность. Для реализации проекта часто могут потребоваться непредвиденные расходы или дополнительные расходы в конце проекта.
Срок окупаемости или «метод окупаемости» – более простая альтернатива NPV. Метод окупаемости рассчитывает, сколько времени потребуется для возврата первоначальных инвестиций. Недостатком является то, что этот метод не учитывает временную стоимость денег. По этой причине сроки окупаемости, рассчитанные для более длительных инвестиций, имеют больший потенциал неточности.
Недостатком является то, что этот метод не учитывает временную стоимость денег. По этой причине сроки окупаемости, рассчитанные для более длительных инвестиций, имеют больший потенциал неточности.
Более того, срок окупаемости строго ограничен временем, необходимым для возврата первоначальных инвестиционных затрат. Не исключено, что рентабельность инвестиций может резко измениться. Сравнение с использованием сроков окупаемости не учитывает долгосрочную прибыльность альтернативных инвестиций.
Чистая приведенная стоимость и внутренняя норма прибыли
Внутренняя норма доходности (IRR) очень похожа на NPV, за исключением того, что ставка дисконтирования – это ставка, которая снижает NPV инвестиции до нуля. Этот метод используется для сравнения проектов с разной продолжительностью жизни или размером необходимого капитала.
Например, IRR можно использовать для сравнения ожидаемой прибыльности трехлетнего проекта, требующего инвестиций в размере 50 000 долларов США, с доходностью 10-летнего проекта, требующего инвестиций в размере 200 000 долларов США. Несмотря на то, что IRR полезен, обычно считается, что он уступает NPV, поскольку делает слишком много предположений о риске реинвестирования и распределении капитала.
Несмотря на то, что IRR полезен, обычно считается, что он уступает NPV, поскольку делает слишком много предположений о риске реинвестирования и распределении капитала.
Суть
Чистая приведенная стоимость (NPV) – это расчет, используемый для определения сегодняшней стоимости будущего потока платежей. Он учитывает временную стоимость денег и может использоваться для сравнения аналогичных инвестиционных альтернатив. NPV основывается на ставке дисконтирования, которая может быть получена из стоимости капитала, необходимого для осуществления инвестиций, и следует избегать любых проектов или инвестиций с отрицательной NPV. Важным недостатком использования анализа NPV является то, что он делает предположения о будущих событиях, которые могут быть ненадежными.
Часто задаваемые вопросы
Что означает чистая приведенная стоимость?
Чистая приведенная стоимость (NPV) – это финансовая метрика, которая направлена на определение общей стоимости потенциальной инвестиционной возможности. Идея NPV состоит в том, чтобы спрогнозировать все будущие поступления и оттоки денежных средств, связанных с инвестициями, дисконтировать все эти будущие денежные потоки к настоящему времени, а затем сложить их вместе. Полученное число после сложения всех положительных и отрицательных денежных потоков вместе – это чистая приведенная стоимость инвестиции. Положительное значение NPV означает, что после учета временной стоимости денег вы заработаете деньги, если продолжите инвестирование.
В чем разница между NPV и IRR?
NPV и IRR – это тесно связанные концепции, поскольку IRR инвестиции – это ставка дисконтирования, при которой NPV будет равна нулю. Другой способ думать об этом заключается в том, что NPV и IRR пытаются ответить на два отдельных, но связанных вопроса. Для NPV возникает вопрос: «Какую общую сумму я заработаю, если продолжу эти инвестиции, с учетом временной стоимости денег?» Для IRR возникает вопрос: «Если я продолжу эти инвестиции, какой будет эквивалентная годовая норма прибыли, которую я получу?»
Что такое хороший NPV?
Теоретически NPV считается «хорошим», если оно больше нуля. В конце концов, расчет NPV уже принимает во внимание такие факторы, как стоимость капитала инвестора, альтернативные издержки и устойчивость к риску через ставку дисконтирования. Также учитываются будущие денежные потоки проекта, а также временная стоимость денег. Следовательно, даже чистая приведенная стоимость в 1 доллар теоретически должна считаться «хорошей». Однако на практике многие инвесторы будут настаивать на определенных пороговых значениях NPV, таких как 10 000 долларов США или выше, чтобы обеспечить себе дополнительный запас прочности .
Статья подготовлена NESrakonk.ru
#ЧЧистая приведенная стоимость (NPV). Расчет чистой приведенной стоимости :: BusinessMan.ru
Инвестиции будут оправданы лишь тогда, когда они способствуют созданию новых ценностей для владельца капитала. В этом случае определяется стоимость данных ценностей, превышающая расходы на их приобретение. Безусловно, возникает вопрос о том, можно ли оценить их больше реальной стоимости. Это доступно в том случае, если конечный результат более ценен в сравнении с суммарной ценой отдельных этапов, реализация которых позволила достичь этого результата. Для того чтобы понять это, следует узнать, что представляет собой чистая приведенная стоимость и как она рассчитывается.
Что такое приведенная стоимость?
Текущая или приведенная стоимость рассчитывается на базе концепции денег во времени. Она представляет собой показатель потенциала средств, направляемых на получение дохода. Она позволяет понять, сколько будет стоить в будущем сумма, которая доступна в настоящее время. Проведение соответствующего расчета имеет большое значение, так как платежи, которые совершены в различный период, могут поддаваться сравнению только после их приведения к одному временному отрезку.
Текущая стоимость образовывается в результате приведения к начальному периоду будущих поступлений и затрат средств. Она зависит от того, каким способом производится начисление процентов. Для этого используются простые или сложные проценты, а также аннуитет.
Что такое чистая приведенная стоимость?
Чистая приведенная стоимость NPV представляет собой разницу между рыночной ценой конкретного проекта и расходами на его реализацию. Аббревиатура, которая используется для ее обозначения, расшифровывается как Net Present Value.
Таким образом, понятие также можно определить как меру добавочной стоимости проекта, которая будет получена в результате его финансирования на начальном этапе. Главная задача состоит в том, чтобы реализовывать проекты, которые имеют положительный показатель чистой приведенной стоимости. Однако для начала следует научиться определять его, что поможет совершать наиболее выгодные инвестиции.
Основное правило NPV
Следует ознакомиться с основным правилом, которым обладает чистая приведенная стоимость инвестиций. Оно заключается в том, что величина показателя должна быть положительной для рассмотрения проекта. Его следует отклонить при получении отрицательного значения.
Стоит отметить, что рассчитываемая величина редко равна нулю. Однако при получении такого значения инвестору также желательно отвергнуть проект, так как он не будет иметь экономического смысла. Это обусловлено тем, что прибыль от вложения в дальнейшем не будет получена.
Точность расчета
В процессе расчета NPV стоит помнить о том, что ставка дисконтирования и прогнозы поступлений оказывают значительное влияние на текущую стоимость. В конечном результате могут быть погрешности. Это объясняется тем, что человек не может с абсолютной точностью сделать прогноз на получение прибыли в будущем. Следовательно, полученный показатель является только предположением. Он не застрахован от колебаний в разные стороны.
Безусловно, инвестору необходимо знать, какая прибыль будет им получена еще до вложения. Чтобы отклонения были минимальными, следует использовать наиболее точные методы для определения эффективности по совместительству с чистой приведенной стоимостью. Общее употребление различных методов позволит понять, будут ли выгодными вложения в определенный проект. Если инвестор уверен в правильности своих расчетов, можно принять решение, которое будет надежным.
Формула расчета
При поиске программ для определения чистой приведенной стоимости можно столкнуться с понятием «чистый дисконтированный доход», что имеет аналогичное определение. Рассчитать ее можно с помощью MS EXCEL, где она встречается под аббревиатурой ЧПС.
В применяемой формуле используются следующие данные:
- CFn – денежная сумма за период n;
- N – количество периодов;
- i – ставка дисконтирования, которая вычисляется из годовой процентной ставки
Кроме того, денежный поток за определенный период может быть нулевым, что эквивалентно его полному отсутствию. При определении дохода денежная сумма записывается со знаком «+», для расходов — со знаком «-«.
В итоге расчет чистой приведенной стоимости приводит к возможности оценки эффективности вложений. Если NPV>0, инвестиция окупится.
Ограничения в применении
Пытаясь определить, какой будет чистая приведенная стоимость NPV, с помощью предложенной методики, следует обратить внимание на некоторые условия и ограничения.
В первую очередь принимается предположение, которое состоит в том, что показатели инвестиционного проекта на протяжении его реализации будут стабильными. Однако вероятность этого может приблизиться к нулю, так как большое количество факторов влияет на величину денежных потоков. Спустя определенное время может измениться стоимость капитала, направленного на финансирование. Следует отметить, что в будущем полученные показатели могут значительно измениться.
Не менее важным моментом является выбор ставки дисконтирования. В качестве нее можно применить стоимость капитала, привлекаемого для инвестирования. С учетом фактора риска ставка дисконтирования может корректироваться. К ней прибавляется надбавка, поэтому чистая приведенная стоимость уменьшается. Подобная практика не всегда является оправданной.
Использование надбавки за риск означает, что инвестором в первую очередь рассматривается только получение убытка. Он по ошибке может отклонить прибыльный проект. Ставкой дисконтирования также может выступать доходность от альтернативных инвестиций. К примеру, если капитал, применяемый для инвестирования, будет вложен в другое дело со ставкой в 9%, ее можно принять за ставку дисконтирования.
Преимущества использования методики
Расчет чистой текущей стоимости имеет следующие преимущества:
- показатель учитывает коэффициент дисконтирования;
- при принятии решения используются четкие критерии;
- возможность использования при расчете рисков проекта.
Однако стоит учитывать, что данный метод имеет не только достоинства.
Недостатки использования методики
Чистая приведенная стоимость инвестиционного проекта обладает следующими отрицательными качествами:
- В некоторых ситуациях довольно проблематично выполнить корректный расчет ставки дисконтирования. Это чаще всего касается многопрофильных проектов.
- Несмотря на то, что денежные потоки прогнозируются, с помощью формулы невозможно рассчитать вероятность исхода события. Применяемый коэффициент может учитывать инфляцию, но в основном ею выступает норма прибыли, закладываемая в расчетный проект.
После подробного ознакомления с понятием «чистая приведенная стоимость» и порядком расчета, инвестор может сделать вывод о том, стоит ли использовать рассматриваемую методику. Для определения эффективности вложений ее желательно дополнить другими похожими способами, что позволит получить наиболее точный результат. Однако нет абсолютной вероятности, что он будет соответствовать действительному получению прибыли или убытка.
| Subject area | English | Russian |
| gen. | accumulated net present value | накопленный дисконтированный поток денежной наличности (Alexander Demidov) |
| insur. | actuarial present value | актуарная дисконтированная стоимость (о пенсиях) |
| audit. | actuarial present value of promised retirement benefit | актуарная дисконтированная стоимость причитающихся пенсий |
| account. | adjusted present value | скорректированная дисконтированная ценность (сокр. APV) |
| st.exch. | adjusted present value | скорректированная приведенная стоимость (dimock) |
| invest. | adjusted present value | скорректированная текущая стоимость (APV) |
| account. | adjusted present value | текущая дисконтированная ценность (сокр. APV) |
| fin. | adjusted-present-value rule | метод скорректированной приведённой стоимости |
| gen. | compound interest / present-value method | метод сложных процентов |
| gen. | compound present-value method | метод сложных процентов (Lavrov) |
| account. | discounted present value | дисконтированная текущая стоимость (Dashout) |
| account. | discounted present value | см. present discounted value (Dashout) |
| fin. | excess present value index | индекс избыточной текущей ценности (igisheva) |
| account. | excess present value index | индекс избыточной текущей дисконтированной ценности |
| account. | excess present value index | индекс рентабельности (отношение текущей дисконтированной ценности, будущего потока денежных средств к первоначальной инвестиции) |
| O&G, sahk.s. | expected net present value | расчётная чистая приведённая стоимость (ЧПС) |
| O&G, sahk.s. | expected net present value | ожидаемая чистая приведённая стоимость |
| O&G, sahk.s. | expected net present value | расчётный чистый приведённый эффект |
| EBRD | FNPV/C, Financial net present value of the investment | Финансовая чистая дисконтированная стоимость инвестиции (Edith) |
| EBRD | FNPV/K, Financial net present value on national capital | Финансовая чистая дисконтированная стоимость на национальный капитал (Edith) |
| invest. | net adjusted present value | чистая скорректированная текущая стоимость |
| energ.ind. | net present value | чистая приведенная стоимость (чистый дисконтированный доход, сумма денежных потоков по всем этапам проекта, экономическая выгода заказчика при реализации новых технологий) |
| account. | net present value | нетто-текущая/дисконтированная стоимость (приведённая/дисконтированная стоимость будущих дополнительных поступлений денежных средств, ожидаемых от данных активов (assets) за вычетом текущей/дисконтированной стоимости дополнительных выплат денежных средств) |
| account. | net present value | чистая текущая стоимость |
| account. | net present value | чистая дисконтированная стоимость (сокр. NPV) |
| account. | net present value | текущая дисконтированная стоимость (сокр. NPV) |
| tech. | net present value | чистая текущая дисконтированная стоимость |
| invest. | net present value | чистая текущая стоимость (NPV) |
| IMF. | net present value | чистая дисконтированная стоимость |
| EBRD | net present value NPV | чистая приведённая стоимость (raf) |
| O&G, karach. | net present value | ЧПС (Aiduza) |
| SAP.tech. | net present value | чистая стоимость |
| oil | net present value | чистая приведённая стоимость (ЧПС) |
| oil | net present value | дисконтированный поток наличности (сумма прибыли уменьшенная на величину инвестиций Seregaboss) |
| invest. | net present value | чистый дисконтированный эффект (igisheva) |
| invest. | net present value | чистый текущий эффект (igisheva) |
| invest. | net present value | чистый текущий доход (igisheva) |
| invest. | net present value | чистый приведённый доход (igisheva) |
| manag. | net present value | чистая приведённая текущая стоимость (Dashout) |
| O&G, sakh. | net present value | ЧДД (NPV; ЧПС — (a sum of the discounted net cash flow over the accounting period, determined by a particular formula)) |
| econ. | net present value | чистая текущая стоимость будущего платежа, исчисленная на основе определённой процентной ставки |
| econ. | net present value | чистый дисконтированный доход |
| med. | net present value | настоящая стоимость будущих поступлений |
| account. | net present value approach | метод оценки по чистой приведенной стоимости (Alexander Matytsin) |
| account. | net present value criterion | критерий чистой дисконтированной стоимости |
| econ. | net present value criterion | критерий чистой стоимости, приведённой к настоящему времени |
| insur. | net present value method | метод оценки чистой приведённой стоимости (NPV) |
| EBRD | net present value method | учёт по приведённым затратам |
| EBRD | net present value method | учёт по чистой дисконтированной стоимости |
| account. | net present value method | метод чистой текущей дисконтированной стоимости |
| IMF. | net present value of debt HIPC Initiative | ЧВП долга |
| IMF. | net present value of debt HIPC Initiative | чистая приведенная стоимость долга |
| IMF. | net present value of debt-to-export ratio HIPC Initiative | отношение ЧПС долга к экспорту |
| IMF. | net present value of debt-to-export ratio HIPC Initiative | отношение чистой приведенной стоимости долга к экспорту |
| IMF. | net present value of debt-to-fiscal revenue target HIPC Initiative | целевое отношение чистой приведенной стоимости ЧПС долга к доходам бюджета |
| invest. | net present value of future investments | чистая текущая стоимость будущих инвестиций |
| invest. | net present value of growth opportunities | чистая текущая стоимость возможностей перспектив роста |
| fin. | Net Present Value of Returns NPVR | Индекс доходности инвестиций (essie) |
| invest. | net present value rule | правило чистой текущей стоимости |
| account. | net present value rule | правило чистой приведённой стоимости |
| IMF. | present discounted value | приведенная стоимость |
| account. | present discounted value | приведённая дисконтированная стоимость |
| account. | present discounted value | приведённая дисконтированная стоимость (то же, что present value) |
| account. | present discounted value | дисконтированная стоимость |
| econ. | present discounted value | текущая дисконтированная стоимость |
| stat. | present discounted value of debt | задолженность по действующей учётной ставке |
| busin. | present utilization value | текущая потребительская стоимость |
| busin. | present value | текущая цена |
| st.exch. | present value | приведенная ценность (dimock) |
| Makarov. | present value | стоимость в существующих ценах |
| O&G, sakh. | present value | приведенная стоимость (PV) |
| account. | present value | текущая ценность (текущий денежный эквивалент будущей суммы средств) |
| account. | present value | дисконтированная стоимость (сокр. PV) см. ru.wikipedia.org/wiki/Дисконтированная_стоимость) |
| account. | present value | приведённая стоимость (сокр. PV) см. ru.wikipedia.org/wiki/Дисконтированная_стоимость Stas-Soleil) |
| SAP.fin. | present value | чистая стоимость |
| account. | present value | текущая стоимость (противоположным является future value — «будущая» стоимость) |
| IMF. | present value | дисконтированная стоимость |
| econ. | present value | фактическая стоимость (с учётом ожидаемой стоимости будущих денежных потоков; в отличие от текущей стоимости — current value — определяемой по текущим рыночным ценам Шандор) |
| bank. | present value | текущая стоимость |
| EBRD | present value | дисконтированная стоимость (PV) |
| EBRD | present value | восстановительная стоимость |
| econ. | present value | существующая цена (Азери) |
| adv. | present value | текущее значение |
| law | present value | настоящая ценность |
| Makarov. | present value | балансовая стоимость |
| SAP.fin. | present value concept | концепция чистой стоимости |
| invest. | present value factor | фактор текущей стоимости |
| invest. | present value factor | дисконтный множитель (felog) |
| gen. | present value factor | коэффициент текущей стоимости (Alexander Demidov) |
| st.exch. | present value formula | формула текущей стоимости (dimock) |
| O&G | present value index | Коэффициент приведения (Множитель, используемый для приведения расходов и доходов более поздних периодов к моменту осуществления первоначальных капиталовложений) |
| O&G | present value index | Коэффициент дисконтирования (Множитель, используемый для приведения расходов и доходов более поздних периодов к моменту осуществления первоначальных капиталовложений) |
| O&G | present value index | показатель приведённой стоимости (PVI serz) |
| busin. | present value index | индекс текущей стоимости |
| oil | present value index | приведённая текущая стоимость (инвестиций andrushin) |
| tech. | present value index | приведённая стоимость |
| mil., avia. | present value life-cycle cost | полные затраты на эксплуатацию системы в существующих ценах |
| econ. | present value method | метод приведения к текущей стоимости |
| econ. | present value method | метод приведения будущих платежей к текущей стоимости |
| construct. | present value method | метод текущей цены |
| audit. | present value of a defined benefit obligation | дисконтированная стоимость обязательств по пенсионному плану с установленными выплатами |
| insur. | present value of a life assurance policy | текущая стоимость полиса страхования жизни |
| bank. | present value of annuity | текущее значение аннуитета (Andy) |
| account. | present value of assets | приведённая стоимость активов |
| account. | present value of business unit | приведённая стоимость деловой единицы |
| account. | present value of cash flow | приведённая стоимость денежного потока |
| account. | present value of discount cash flow | приведённая стоимость дисконтированного денежного потока |
| busin. | present value of future flow of funds | текущая стоимость будущего движения денежных средств |
| invest. | present value of growth opportunities | текущая стоимость возможностей роста |
| account. | present value of headquarters | приведённая стоимость головного офиса |
| O&G | present value of investment | приведённая стоимость инвестиций (PVI, ПСИ serz) |
| busin. | present value of life assurance policy | текущая стоимость полиса страхования жизни |
| account. | present value of life policy | текущая дисконтированная стоимость финансовых обязательств страховщика по договору страхования жизни |
| account. | present value of life policy | текущая приведённая стоимость финансовых обязательств страховщика по договору страхования жизни |
| econ. | present value of life policy | современная стоимость финансовых обязательств страховщика по договору страхования жизни |
| O&G | present value profit | текущая стоимость будущих доходов при данной учётной ставке |
| econ. | present value profit | текущая прибыль (PVP) |
| O&G | present value profit/investment | коэффициент реальной эффективности капиталовложений |
| econ. | present value tables | таблицы приведённой текущей стоимости |
| econ. | present value tables | таблица дисконтированной стоимости будущих платежей |
| econ. | present value tables | таблицы текущей стоимости (по срокам и ставкам дисконта) |
| econ. | present value tables | таблицы приведённой стоимости |
| econ. | present value tables | таблицы приведённой стоимости (по срокам, и ставкам дисконта) |
| econ. | present value tables | таблицы приведённой дисконтированной стоимости (по срокам и ставкам дисконта) |
| econ. | specific net present value SNPV | приведенная чистая стоимость (Sergei Aprelikov) |
| math. | the functional gives the present value | действительное значение (of the stress T (x,t) at the material point when …) |
| math. | the present value of the stress depends in an arbitrary way on the entire history of deformation gradient | зависеть произвольно от |
| mech. | The value of the constant is irrelevant to the present discussion | Значение этой константы не существенно для наших рассуждений |
Чистая приведенная стоимость (NPV) Определение
Что такое чистая приведенная стоимость (ЧПС)?
Чистая приведенная стоимость (NPV) — это разница между текущей стоимостью денежных поступлений и текущей стоимостью оттока денежных средств за период времени. NPV используется при составлении бюджета капиталовложений и инвестиционном планировании для анализа прибыльности планируемых инвестиций или проектов. NPV — это результат вычислений, используемых для определения сегодняшней стоимости будущего потока платежей.
Ключевые выводы
- Чистая приведенная стоимость, или NPV, используется для расчета текущей общей стоимости будущего потока платежей.
- Если NPV проекта или инвестиции положительна, это означает, что дисконтированная приведенная стоимость всех будущих денежных потоков, связанных с этим проектом или инвестицией, будет положительной и, следовательно, привлекательной. t} \\ & \ textbf {где:} \\ & R_t = \ text {Чистый приток денежных средств- отток за один период} t \\ & i = \ text {Ставка дисконтирования или доход, который может быть получен в} \\ & \ text {альтернативных инвестициях} \\ & t = \ text {Количество периодов таймера} \\ \ end { выровнен}
NPV = t = 1∑n (1 + i) tRt, где: Rt = чистый приток-отток денежных средств в течение одного периода ti = ставка дисконтирования или доход, который может быть получен за счет альтернативных инвестиций st = количество периодов таймера
Если вы не знакомы с обозначением суммирования, вот более простой способ запомнить концепцию NPV:
ЧПС знак равно TVECF — TVIC куда: TVECF знак равно Сегодняшняя стоимость ожидаемых денежных потоков TVIC знак равно Сегодняшняя стоимость вложенных денежных средств \ begin {align} & \ textit {NPV} = \ text {TVECF} — \ text {TVIC} \\ & \ textbf {где:} \\ & \ text {TVECF} = \ text {Сегодняшняя сумма ожидаемых денежных средств потоки} \\ & \ text {TVIC} = \ text {Сегодняшняя стоимость вложенных денежных средств} \\ \ end {выровнено} NPV = TVECF − TVIC, где: TVECF = сегодняшняя стоимость ожидаемых денежных потоков TVIC = сегодняшняя стоимость инвестированных денежных средств.
О чем может вам рассказать чистая приведенная стоимость
NPV учитывает временную стоимость денег и может использоваться для сравнения аналогичных инвестиционных альтернатив.NPV основывается на ставке дисконтирования, которая может быть получена из стоимости капитала, необходимого для инвестирования, и следует избегать любых проектов или инвестиций с отрицательной NPV. Одним из важных недостатков анализа NPV является то, что он делает предположения о будущих событиях, которые могут быть ненадежными.
NPV рассчитывает оценить прибыльность данной инвестиции, исходя из того, что доллар в будущем не будет стоить столько же, сколько доллар сегодня. Деньги со временем теряют ценность из-за инфляции. Однако доллар сегодня можно инвестировать и получить прибыль, в результате чего его будущая стоимость, возможно, будет выше, чем доллар, полученный в тот же момент в будущем.
NPV направлена на определение приведенной стоимости будущих денежных потоков инвестиций сверх первоначальной стоимости инвестиции. Элемент ставки дисконтирования формулы NPV дисконтирует будущие денежные потоки до текущей стоимости. Если вычитание первоначальной стоимости инвестиций из суммы денежных потоков на сегодняшний день положительно, тогда вложение оправдано.
Например, инвестор может получить 100 долларов сегодня или через год. Большинство инвесторов не захотели бы откладывать получение 100 долларов сегодня.Однако что, если инвестор мог бы выбрать получение 100 долларов сегодня или 105 долларов через год? Ставка доходности 5% для ожидания в течение одного года может быть выгодной для инвестора, если только другие инвестиции не могут принести доход более 5% за тот же период.
Если бы инвестор знал, что он может заработать 8% от относительно безопасных инвестиций в течение следующего года, он бы предпочел получить 100 долларов сегодня, а не 105 долларов в год, с 5% -ной нормой прибыли. В этом случае ставкой дисконтирования будет 8%.
Положительный и отрицательный NPV
Положительное значение NPV указывает на то, что прогнозируемая прибыль от проекта или инвестиций — в текущих долларах — превышает ожидаемые затраты, также в текущих долларах. Предполагается, что инвестиции с положительной NPV будут прибыльными.
Инвестиция с отрицательной NPV приведет к чистому убытку. Эта концепция является основой правила чистой приведенной стоимости, согласно которому следует рассматривать только инвестиции с положительными значениями NPV.
Расчет чистой приведенной стоимости
Деньги в настоящем стоят больше, чем такая же сумма в будущем, из-за инфляции и возможных доходов от альтернативных инвестиций, которые можно было бы сделать в промежуточный период. Другими словами, доллар, заработанный в будущем, не будет стоить столько же, сколько доллар, заработанный в настоящем. Элемент ставки дисконтирования формулы NPV позволяет учесть это.
Например, предположим, что инвестор может выбрать платеж в размере 100 долларов сегодня или через год.Рациональный инвестор не захочет откладывать платеж. Однако что, если бы инвестор мог выбрать получение 100 долларов сегодня или 105 долларов в год? Если плательщик был надежным, то эти дополнительные 5%, возможно, стоили ожидания, но только в том случае, если не было ничего другого, что инвесторы могли бы сделать со 100 долларами, которые принесут более 5%.
Инвестор может подождать год, чтобы заработать дополнительные 5%, но это может быть приемлемо не для всех инвесторов. В этом случае 5% — это ставка дисконтирования, которая будет варьироваться в зависимости от инвестора.Если бы инвестор знал, что он может заработать 8% от относительно безопасного вложения в течение следующего года, он не захотел бы откладывать выплату 5%. В этом случае ставка дисконтирования инвестора составляет 8%.
Компания может определить ставку дисконтирования, используя ожидаемую доходность других проектов с аналогичным уровнем риска или стоимость заимствования денег, необходимых для финансирования проекта. Например, компания может избежать проекта, который, как ожидается, будет приносить 10% в год, если финансирование проекта стоит 12%, или альтернативный проект, как ожидается, будет приносить 14% в год.
Представьте, что компания может инвестировать в оборудование, которое будет стоить 1 000 000 долларов и, как ожидается, будет приносить 25 000 долларов дохода в месяц в течение пяти лет. Компания имеет доступный капитал для приобретения оборудования и может в качестве альтернативы инвестировать его в фондовый рынок с ожидаемой доходностью 8% в год. Менеджеры считают, что покупка оборудования или инвестирование в фондовый рынок — аналогичные риски.
NPV можно рассчитать с помощью таблиц, электронных таблиц (например, Excel) или финансовых калькуляторов.
Шаги к чистой приведенной стоимости
Есть два основных шага для расчета NPV:
Шаг 1: ЧПС первоначальной инвестиции
Поскольку оборудование оплачивается авансом, это первый денежный поток, включенный в расчет. Нет необходимости учитывать затраченное время, поэтому не нужно сбрасывать со счетов сегодняшний отток в размере 1 000 000 долларов.
- Определите количество периодов (t): Предполагается, что оборудование будет генерировать ежемесячный денежный поток и прослужит пять лет, что означает, что в расчет будет включено 60 денежных потоков и 60 периодов.{\ frac {1} {12}}) — 1 = 0,64 \%
Периодическая ставка = ((1 + 0,08) 121) -1 = 0,64%
Шаг 2: NPV будущих денежных потоков
Предположим, что ежемесячные денежные потоки зарабатываются в конце месяца, а первый платеж поступает ровно через месяц после покупки оборудования. Это будущий платеж, поэтому его необходимо скорректировать с учетом временной стоимости денег. Инвестор может легко выполнить этот расчет с помощью электронной таблицы или калькулятора. Чтобы проиллюстрировать концепцию, первые пять платежей показаны в таблице ниже.
Изображение Сабрины Цзян © Investopedia 2020Полный расчет приведенной стоимости равен приведенной стоимости всех 60 будущих денежных потоков за вычетом инвестиций в размере 1 000 000 долларов США. Расчет мог бы быть более сложным, если бы предполагалось, что оборудование будет иметь какое-либо значение, оставшееся в конце его срока службы, но в этом примере предполагается, что оно бесполезно.
N п V знак равно — $ 1 , 000 , 000 + ∑ т знак равно 1 60 25 , 00 0 60 ( 1 + 0,0064 ) 60 ЧПС = — \ 1 000 000 долл. {60} \ frac {25 000_ {60}} {(1 + 0.{60}} NPV = — 1 000 000 долларов США + ∑t = 160 (1 + 0,0064) 6025 00060
Эту формулу можно упростить до следующего расчета:
N п V знак равно — $ 1 , 000 , 000 + $ 1 , 242 , 322,82 знак равно $ 242 , 322,82 NPV = — \ 1000000 + \ 1 242 322,82 доллара = \ 242 322,82 доллара NPV = — 1 000 000 долларов США + 1 242 322,82 доллара США = 242 322,82 доллара США
В этом случае ЧПС положительна; оборудование следует покупать. Если приведенная стоимость этих денежных потоков была отрицательной, потому что ставка дисконтирования была больше, или чистые денежные потоки были меньше, инвестиций следовало бы избежать.
Ограничения чистой приведенной стоимости
Оценка прибыльности инвестиций с помощью NPV в значительной степени зависит от предположений и оценок, поэтому может существовать существенная возможность для ошибки. Предполагаемые факторы включают инвестиционные затраты, ставку дисконтирования и прогнозируемую доходность. Для реализации проекта часто могут потребоваться непредвиденные расходы или могут потребоваться дополнительные расходы в конце проекта.
Чистая приведенная стоимость к сроку окупаемости
Срок окупаемости или «метод окупаемости» — более простая альтернатива NPV.Метод окупаемости рассчитывает, сколько времени потребуется для возврата первоначальных инвестиций. Недостатком является то, что этот метод не учитывает временную стоимость денег. По этой причине сроки окупаемости, рассчитанные для более длительных вложений, имеют больший потенциал неточности.
Более того, срок окупаемости строго ограничен временем, необходимым для возврата первоначальных инвестиционных затрат. Не исключено, что рентабельность инвестиций может резко измениться.Сравнение с использованием сроков окупаемости не учитывает долгосрочную прибыльность альтернативных инвестиций.
NPV и внутренняя норма доходности (IRR)
Внутренняя норма доходности (IRR) очень похожа на NPV, за исключением того, что ставка дисконтирования — это ставка, которая снижает NPV инвестиции до нуля. Этот метод используется для сравнения проектов с разной продолжительностью жизни или размером необходимого капитала.
Например, IRR можно использовать для сравнения ожидаемой прибыльности трехлетнего проекта, требующего инвестиций в размере 50 000 долларов США, с доходностью 10-летнего проекта, требующего инвестиций в размере 200 000 долларов США.Несмотря на то, что IRR полезен, обычно считается, что он уступает NPV, поскольку делает слишком много предположений о риске реинвестирования и распределении капитала.
Что означает чистая приведенная стоимость?
Чистая приведенная стоимость (NPV) — это финансовая метрика, которая направлена на определение общей стоимости потенциальной инвестиционной возможности. Идея NPV состоит в том, чтобы спрогнозировать все будущие поступления и оттоки денежных средств, связанных с инвестициями, дисконтировать все эти будущие потоки денежных средств к настоящему времени, а затем сложить их вместе.Полученное число после сложения всех положительных и отрицательных денежных потоков представляет собой чистую приведенную стоимость инвестиции. Положительное значение NPV означает, что после учета временной стоимости денег вы заработаете деньги, если продолжите инвестирование.
В чем разница между NPV и IRR?
NPV и IRR — это тесно связанные концепции в том смысле, что IRR инвестиции — это ставка дисконтирования, которая приведет к тому, что NPV этой инвестиции будет равна нулю. Другой способ думать об этом заключается в том, что NPV и IRR пытаются ответить на два отдельных, но связанных вопроса.Для NPV возникает вопрос: «Какую общую сумму я заработаю, если продолжу эти инвестиции, с учетом временной стоимости денег?» Для IRR возникает вопрос: «Если я продолжу эти инвестиции, какой будет эквивалентная годовая норма прибыли, которую я получу?»
Что такое хороший NPV?
Теоретически чистая приведенная стоимость считается «хорошей», если она больше нуля. В конце концов, расчет NPV уже принимает во внимание такие факторы, как стоимость капитала инвестора, альтернативные издержки и толерантность к риску через ставку дисконтирования.Также учитываются будущие денежные потоки проекта, а также временная стоимость денег. Следовательно, даже чистая приведенная стоимость в 1 доллар теоретически должна считаться «хорошей». На практике, однако, многие инвесторы будут настаивать на определенных порогах NPV, таких как 10 000 долларов и выше, чтобы обеспечить себе дополнительный запас прочности.
Почему будущие денежные потоки дисконтируются?
NPV использует дисконтированные денежные потоки, обусловленные временной стоимостью денег (TMV). Временная стоимость денег — это концепция, согласно которой деньги, которые у вас есть сейчас, стоят больше, чем идентичная сумма в будущем, из-за их потенциальной доходности за счет инвестиций и других факторов, таких как инфляционные ожидания.Ставка, используемая для учета времени, или ставка дисконтирования, будет зависеть от типа проведенного анализа. Отдельные лица должны использовать альтернативные издержки использования своих денег в другом месте в качестве подходящей ставки дисконтирования — проще говоря, это норма прибыли, которую инвестор может получить на рынке на вложения сопоставимого размера и риска.
Разница между приведенной стоимостью (PV) и чистой приведенной стоимостью (NPV)
Приведенная стоимость (PV) — это текущая стоимость будущей денежной суммы или денежного потока при заданной норме прибыли.Между тем, чистая приведенная стоимость (NPV) — это разница между текущей стоимостью денежных поступлений и текущей стоимостью оттока денежных средств за период времени.
Основное различие между PV и NPV
Хотя и PV, и NPV используют форму дисконтированных денежных потоков для оценки текущей стоимости будущего дохода, эти расчеты отличаются в одном важном отношении. Формула NPV учитывает начальные капитальные затраты, необходимые для финансирования проекта, что делает его чистым показателем, в то время как расчет PV учитывает только приток денежных средств.
Хотя понимание концепции, лежащей в основе расчета PV, важно, формула NPV является гораздо более полным индикатором потенциальной прибыльности данного проекта.
Поскольку стоимость дохода, полученного сегодня, выше, чем доход, полученный в будущем, предприятия дисконтируют будущий доход с учетом ожидаемой нормы прибыли от инвестиций. Эта ставка, называемая минимальной ставкой, представляет собой минимальную норму прибыли, которую проект должен генерировать, чтобы бизнес рассмотрел возможность инвестирования в него.
Расчет PV и NPV
Расчет PV показывает дисконтированную стоимость всех доходов, полученных от проекта, в то время как NPV показывает, насколько прибыльным будет проект после учета начальных инвестиций, необходимых для его финансирования.
Формула для расчета NPV выглядит следующим образом:
ЧПС знак равно поток наличных денег ÷ ( 1 + я ) * т — первоначальное вложение куда: я знак равно требуемая ставка или ставка дисконтирования т знак равно количество периодов времени \ begin {align} & \ text {NPV} = \ text {денежный поток} \ div (1 + i) * t — \ text {начальные инвестиции} \\ & \ textbf {где:} \\ & i = \ text { требуемая ставка или ставка дисконтирования} \\ & t = \ text {количество периодов времени} \\ \ end {выровнено} NPV = денежный поток ÷ (1 + i) ∗ t — начальные инвестиции, где: i = требуемая ставка или ставка дисконтирования t = количество периодов времени
Например, предположим, что для данного проекта требуются первоначальные капитальные вложения в размере 15 000 долларов США.3} = \ 23 807 долл. США (1 + 0,07) 1 3500 долларов США + (1 + 0,07) 2 9 400 долларов США + (1 + 0,07) 3 15 100 долларов США = 23 807 долларов США
Чистая приведенная стоимость этого проекта может быть определена путем простого вычитания начальных капитальных вложений из дисконтированной выручки:$ 23 , 807 — $ 15 , 000 знак равно $ 8 , 807 23 807 долларов — 15 000 = 8 807 долларов 23 807 долларов — 15 000 = 8 807 долларов
Как рассчитать чистую приведенную стоимость (NPV)
Итог
Хотя значение PV полезно, расчет NPV неоценим для составления бюджета капиталовложений.Проект с высоким значением PV может иметь гораздо менее впечатляющую NPV, если для его финансирования требуется большой капитал. По мере расширения бизнес стремится финансировать только те проекты или инвестиции, которые приносят наибольшую прибыль, что, в свою очередь, обеспечивает дополнительный рост. При наличии ряда потенциальных вариантов обычно рассматривается проект или инвестиция с наивысшей NPV.
Повторное знакомство с чистой приведенной стоимостью
Большинство людей знают, что деньги, которые у вас есть сейчас, более ценны, чем деньги, которые вы соберете позже.Это потому, что вы можете использовать его, чтобы заработать больше денег, управляя бизнесом, или покупая что-то сейчас и продавая позже, или просто кладя это в банк и получая проценты. Будущие деньги также менее ценны, потому что инфляция подрывает их покупательную способность. Это называется временной стоимостью денег . Но как именно сравнить стоимость денег сейчас и стоимость денег в будущем? Вот где появляется чистая приведенная стоимость .
Чтобы узнать больше о том, как можно использовать чистую приведенную стоимость для перевода стоимости инвестиций в сегодняшние доллары, я поговорил с Джо Найтом, соавтором книги Financial Intelligence: A Manager’s Guide to Know What the Numbers Really Mean и соучредителем и владелец www.business-literacy.com.
Что такое чистая приведенная стоимость?
«Чистая приведенная стоимость — это приведенная стоимость денежных потоков при требуемой норме доходности вашего проекта по сравнению с вашими первоначальными инвестициями», — говорит Найт. На практике это метод расчета рентабельности инвестиций или рентабельности инвестиций в проект или расходы. Просматривая все деньги, которые вы ожидаете получить от инвестиций, и переводя эту прибыль в сегодняшние доллары, вы можете решить, стоит ли проект.
Для чего его обычно используют компании?
Когда менеджеру необходимо сравнить проекты и решить, какие из них следует реализовать, обычно доступны три варианта: внутренняя норма прибыли, метод окупаемости и чистая приведенная стоимость. Найт говорит, что чистая приведенная стоимость, часто называемая NPV, является предпочтительным инструментом для большинства финансовых аналитиков. На то есть две причины. Во-первых, NPV учитывает временную стоимость денег , переводя будущие денежные потоки в сегодняшние доллары.Во-вторых, он предоставляет конкретное число, которое менеджеры могут использовать, чтобы легко сравнить первоначальные денежные затраты с текущей стоимостью прибыли.
Другой дубль
«Этот метод намного превосходит наиболее часто используемый метод окупаемости», — говорит он. Привлекательность окупаемости заключается в том, что ее легко рассчитать и понять: когда вы вернете вложенные деньги? Но при этом не учитывается, что покупательная способность денег сегодня больше, чем покупательная способность той же суммы денег в будущем.
Вот что делает NPV лучшим методом, — говорит Найт. И, к счастью, с финансовыми калькуляторами и таблицами Excel теперь почти так же легко рассчитать NPV.
Менеджеры также используют NPV, чтобы решить, делать ли крупные покупки, такие как оборудование или программное обеспечение. Она также используется при слияниях и поглощениях (хотя в этом сценарии она называется моделью дисконтированных денежных потоков ). Фактически, это модель, которую Уоррен Баффет использует для оценки компаний. Каждый раз, когда компания использует сегодняшние доллары для получения прибыли в будущем, NPV — хороший выбор.
Как рассчитать?
Никто не рассчитывает NPV вручную, говорит Найт. В Excel есть функция NPV, которая упрощает задачу после ввода потока затрат и выгод. (Включите «NPV» в функцию «Справка», и вы получите краткое руководство, либо вы можете приобрести HBR Guide to Building Your Business Case + Tools, который включает простую в использовании предварительно заполненную электронную таблицу для NPV и другой рентабельности инвестиций. методы). Многие финансовые калькуляторы также включают функцию NPV.«Такой выродок, как я, у меня он есть на моем iPhone. Мне нравится знать, что он у меня в кармане, — говорит Найт.
Даже если вы не математический ботаник, как Найт, полезно разобраться в математике, лежащей в основе этого. «Даже опытные аналитики могут не помнить или понимать математику, но это довольно просто», — говорит он. Расчет выглядит так:
Это сумма приведенной стоимости денежных потоков (положительных и отрицательных) за каждый год, связанных с инвестициями, дисконтированная таким образом, чтобы она была выражена в сегодняшних долларах.Чтобы сделать это вручную, вы сначала рассчитываете приведенную стоимость прогнозируемой прибыли на каждый год, взяв прогнозируемый денежный поток на каждый год и разделив его на (1 + ставка дисконтирования). Это выглядит так:
Итак, для денежного потока через пять лет уравнение выглядит следующим образом:
Если проект приносит доход за пять лет, вы рассчитываете этот показатель для каждого из этих пяти лет. Затем сложите их вместе. Это будет текущая стоимость всех ваших прогнозируемых доходов.Затем вы вычитаете свои первоначальные инвестиции из этого числа, чтобы получить NPV.
Если NPV отрицательная, значит проект плохой. В конечном итоге это истощит бизнес. Однако в случае положительного результата проект следует принять. Чем больше положительное число, тем больше выгода для компании.
Теперь вам может быть интересно узнать о ставке дисконтирования. Ставка дисконтирования будет зависеть от конкретной компании, поскольку она связана с тем, как компания получает свои средства. Это норма прибыли, которую ожидают инвесторы, или стоимость заимствования денег.Если акционеры ожидают доходности в 12%, это ставка дисконтирования, которую компания будет использовать для расчета NPV. Если фирма платит 4% годовых по своему долгу, то она может использовать эту цифру в качестве ставки дисконтирования. Обычно ставку устанавливает офис финансового директора.
Какие распространенные ошибки делают люди?
Есть две вещи, о которых менеджеры должны знать при использовании NPV. Во-первых, это сложно объяснить другим. Как пишет Найт в своей книге Financial Intelligence , «дисконтированная стоимость будущих денежных потоков — не такая фраза, которую легко сбить с толку нефинансового языка».Тем не менее, по его словам, стоит приложить дополнительные усилия для объяснения и представления NPV из-за его превосходства как метода. Он пишет: «Любая инвестиция, прошедшая тест на чистую приведенную стоимость, увеличит акционерную стоимость, а любая неудачная инвестиция (если все равно будет осуществлена) нанесет вред компании и ее акционерам».
Дополнительная литература
Второе, о чем следует помнить менеджерам, — это то, что расчеты основаны на нескольких предположениях и оценках, а это означает, что есть много места для ошибок.Вы можете снизить риски, дважды проверив свои оценки и проведя анализ чувствительности после того, как сделаете первоначальный расчет.
Есть три места, где вы можете сделать неверные оценки, которые сильно повлияют на конечные результаты ваших вычислений. Во-первых, это первоначальные вложения. Вы знаете, сколько будет стоить проект или расходы? Если вы покупаете оборудование с четкой ценой, риска нет. Но если вы обновляете свою ИТ-систему и делаете оценки относительно времени и ресурсов сотрудников, сроков реализации проекта и того, сколько вы собираетесь платить сторонним поставщикам, цифры могут сильно отличаться.
Во-вторых, существуют риски, связанные со ставкой дисконтирования. Вы используете сегодняшнюю ставку и применяете ее к будущим доходам, поэтому есть вероятность, что, скажем, на третьем году проекта процентные ставки вырастут, а стоимость ваших средств вырастет. Это будет означать, что ваши доходы за этот год будут менее ценными, чем вы изначально думали.
В-третьих, и именно здесь, по словам Найта, люди часто делают ошибки при оценке, вы должны быть относительно уверены в прогнозируемой доходности вашего проекта.«Эти прогнозы обычно оптимистичны, потому что люди хотят реализовать проект или купить оборудование», — говорит он.
Чистая приведенная стоимость (ЧПС) — определение, примеры, как проводить анализ ЧПС
Что такое чистая приведенная стоимость (ЧПС)?
Чистая приведенная стоимость (NPV) — это стоимость всех будущих денежных потоков. Отчет о денежных потоках. в течение всего срока действия вложения со скидкой до настоящего времени.Анализ NPV — это форма внутренней оценки, которая широко используется в финансах. Обзор корпоративных финансов. Корпоративные финансы имеют дело со структурой капитала корпорации, включая ее финансирование и действия, предпринимаемые руководством для увеличения стоимости и учета для определения стоимости бизнеса. инвестиционная безопасность, капитальный проект, новое предприятие, программа сокращения затрат и все, что связано с денежным потоком.
Формула NPV
Формула чистой приведенной стоимости:
Где:
- Z 1 = Денежный поток
- за время Z 2 = Денежный поток во времени 2
- r = Ставка дисконтирования
- X 0 = Денежный отток во времени 0 (т.е.е. цена покупки / первоначальные инвестиции)
Почему используется анализ чистой приведенной стоимости (NPV)?
Анализ NPV используется, чтобы помочь определить, сколько стоит инвестиция, проект или любой ряд денежных потоков. Это всеобъемлющий показатель, поскольку он учитывает все доходы. Доход от продаж. Доход от продаж — это доход, полученный компанией от продажи товаров или оказания услуг. В бухгалтерском учете термины «продажи», расходы и капитальные затраты, связанные с вложением в ее свободный денежный поток (FCF) Свободный денежный поток (FCF) Свободный денежный поток (FCF) измеряют способность компании производить то, что больше всего волнует инвесторов. : наличные деньги распределяются по собственному усмотрению..
Помимо факторинга всех доходов и затрат, он также принимает во внимание сроки каждого денежного потока, которые могут иметь большое влияние на приведенную стоимость инвестиций. Например, лучше увидеть приток денежных средств раньше, а отток — позже, чем наоборот.
Почему денежные потоки дисконтируются?
Денежные потоки в анализе чистой приведенной стоимости дисконтируются по двум основным причинам: (1) для корректировки риска инвестиционной возможности и (2) для учета временной стоимости денег (TVM).
Первый пункт (поправка на риск) необходим, потому что не все предприятия, проекты или инвестиционные возможности имеют одинаковый уровень риска. Другими словами, вероятность получения денежного потока от векселя Казначейства США намного выше, чем вероятность получения денежного потока от молодого технологического стартапа.
Для учета риска ставка дисконтирования выше для более рискованных инвестиций и ниже для более безопасных. Пример казначейства США считается безрисковой ставкой, а все другие инвестиции измеряются тем, насколько больший риск они несут по сравнению с этим.
Второй пункт (для учета временной стоимости денег) необходим, потому что из-за инфляции, процентных ставок и альтернативных издержек деньги тем ценнее, чем раньше они получены. Например, получить 1 миллион долларов сегодня намного лучше, чем 1 миллион долларов, полученный через пять лет. Если деньги будут получены сегодня, их можно будет инвестировать и заработать проценты, так что через пять лет они будут стоить более 1 миллиона долларов.
Пример чистой приведенной стоимости (NPV)
Давайте посмотрим на пример того, как рассчитать чистую приведенную стоимость ряда денежных потоков. Бесплатные руководства по оценке, позволяющие изучать наиболее важные концепции в удобном для вас темпе.Эти статьи научат вас передовым методам оценки бизнеса и научат оценивать компанию с помощью сопоставимого анализа компании, моделирования дисконтированного денежного потока (DCF) и прецедентных транзакций, используемых в инвестиционно-банковских операциях, исследованиях капитала и т. Д. Как вы можете видеть на скриншоте ниже, предполагается, что инвестиция будет приносить доход в размере 10 000 долларов в год в течение 10 лет, а требуемая ставка дисконтирования составляет 10%.
Окончательный результат состоит в том, что стоимость этих инвестиций сегодня составляет 61 446 долларов.Это означает, что рациональный инвестор был бы готов платить до 61 466 долларов сегодня, чтобы получать 10 000 долларов ежегодно в течение 10 лет. Уплатив эту цену, инвестор получит внутреннюю норму доходности. Внутренняя норма доходности (IRR) Внутренняя норма доходности (IRR) — это ставка дисконтирования, которая делает чистую приведенную стоимость (NPV) проекта равной нулю. Другими словами, это ожидаемая совокупная годовая норма прибыли, которая будет получена от проекта или инвестиций. (IRR) 10%. Заплатив меньше 61 000 долларов, инвестор получит внутреннюю норму прибыли более 10%.
Загрузите бесплатный шаблон
Введите свое имя и адрес электронной почты в форму ниже и загрузите бесплатный шаблон прямо сейчас!
Шаблон чистой приведенной стоимости
Загрузите бесплатный шаблон Excel, чтобы углубить свои знания в области финансов!Функции NPV в Excel
Excel предлагает две функции для расчета чистой приведенной стоимости: NPV и XNPV. Эти две функции используют одну и ту же математическую формулу, показанную выше, но экономят время аналитика на ее вычисление в развернутой форме.
Обычная функция NPV = NPV () предполагает, что все денежные потоки в серии происходят с регулярными интервалами (т. Е. Годы, кварталы, месяц), и не допускает каких-либо изменений в эти периоды времени.
Функция XNPV = XNPV () позволяет применять определенные даты к каждому денежному потоку, чтобы они могли быть нерегулярными. Эта функция может быть очень полезной, поскольку денежные потоки часто неравномерно распределены, и требуется повышенный уровень точности.
Внутренняя норма доходности (IRR) и NPV
Внутренняя норма доходности (IRR Внутренняя норма доходности (IRR) Внутренняя норма доходности (IRR) — это ставка дисконтирования, которая составляет чистую приведенную стоимость (NPV) нулевой проект.Другими словами, это ожидаемая совокупная годовая норма прибыли, которая будет получена от проекта или инвестиций.) — это ставка дисконтирования, при которой чистая приведенная стоимость инвестиции равна нулю. Другими словами, это совокупный годовой доход, который инвестор ожидает получить (или фактически заработал) в течение срока действия инвестиции.
Например, если ценная бумага предлагает серию денежных потоков с NPV 50 000 долларов, а инвестор платит за нее ровно 50 000 долларов, то NPV инвестора составляет 0 долларов.Это означает, что они будут зарабатывать независимо от ставки дисконтирования под залог. В идеале инвестор должен заплатить менее 50 000 долларов и, следовательно, получить IRR, превышающую ставку дисконтирования.
Обычно инвесторы и менеджеры бизнеса рассматривают как NPV, так и IRR вместе с другими цифрами при принятии решения. Узнайте о IRR и XIRR в Excel XIRR и IRR Зачем использовать XIRR и IRR. XIRR назначает конкретные даты каждому отдельному денежному потоку, что делает его более точным, чем IRR, при построении финансовой модели в Excel..
Отрицательная и положительная чистая приведенная стоимость
Если чистая приведенная стоимость проекта или инвестиций отрицательна, это означает, что ожидаемая норма прибыли, которая будет получена от них, меньше ставки дисконтирования (требуемая норма прибыли или пороговая ставка Определение пороговой ставки Пороговая ставка, которая также известна как минимально допустимая ставка доходности (MARR), представляет собой минимальную требуемую норму прибыли или целевую ставку, которую инвесторы ожидают получить от инвестиции. Ставка определяется путем оценки стоимости капитала, вовлеченных рисков, текущих возможностей расширения бизнеса, нормы прибыли для аналогичных инвестиций и других факторов).Это не обязательно означает, что проект «потеряет деньги». Он вполне может генерировать бухгалтерскую прибыль (чистую прибыль), но, поскольку полученная норма прибыли меньше ставки дисконтирования, считается, что она снижает стоимость. Если NPV положительна, это создает ценность.
Приложения в финансовом моделировании
NPV бизнеса
Чтобы оценить бизнес, аналитик построит подробную DCF-модель дисконтированного денежного потока DCF-модель Обучение Бесплатное руководствоA DCF-модель — это особый тип финансовой модели, используемой для оценки бизнесс.Эта модель представляет собой просто прогноз неуправляемого свободного денежного потока компании в Excel. Эта финансовая модель будет включать все доходы, расходы, капитальные затраты и детали бизнеса.
После того, как ключевые допущения сделаны, аналитик может построить пятилетний прогноз для трех финансовых отчетов. Три финансовых отчета. Три финансовых отчета — это отчет о прибылях и убытках, баланс и отчет о движении денежных средств. Эти три основных отчета (отчет о прибылях и убытках, баланс и движение денежных средств) и рассчитывают свободный денежный поток фирмы (FCFF). Бесплатные руководства по оценке, позволяющие изучать наиболее важные концепции в удобном для вас темпе.Эти статьи научат вас передовым методам оценки бизнеса и научат оценивать компанию, используя сопоставимый анализ компании, моделирование дисконтированного денежного потока (DCF) и прецедентные транзакции, которые используются в инвестиционно-банковском деле, исследованиях акций, также известном как безрычажный свободный денежный поток. .
Наконец, конечная стоимость используется для оценки компании за пределами прогнозного периода, и все денежные потоки дисконтируются до настоящего времени по средневзвешенной стоимости капитала компании. Чтобы узнать больше, посетите бесплатный подробный курс финансового моделирования CFI.
NPV проекта
Оценить проект обычно проще, чем весь бизнес. Применяется аналогичный подход, когда все детали проекта моделируются в Excel, однако период прогноза будет на весь срок существования проекта, и конечной стоимости не будет. После того, как свободный денежный поток рассчитан, его можно дисконтировать до настоящего времени либо по WACCWACCWACC фирмы — это средневзвешенная стоимость капитала фирмы, которая представляет собой смешанную стоимость капитала, включая собственный капитал и заемные средства.или соответствующий барьер.
Недостатки чистой приведенной стоимости
Хотя чистая приведенная стоимость (ЧПС) является наиболее часто используемым методом оценки инвестиционных возможностей, у него есть некоторые недостатки, которые следует тщательно учитывать.
Основные проблемы анализа NPV включают:
- Необходимо составить длинный список предположений
- Чувствительность к небольшим изменениям в предположениях и драйверах Моделирование оценки в Excel Моделирование оценки в Excel может относиться к нескольким различным типам анализа, включая дисконтированный денежный поток (DCF) анализ, сопоставимые торговые мультипликаторы
- Легко манипулируют для получения желаемого результата
- Может не улавливать выгоды / последствия второго и третьего порядка (т.е.д., в других частях бизнеса)
- Предполагается, что ставка дисконтирования будет постоянной с течением времени
- Точная корректировка рисков является сложной задачей (трудно получить данные о корреляциях, вероятностях)
Дополнительные ресурсы
Чистая приведенная стоимость (NPV) — наиболее подробный и широко используемый метод оценки привлекательности инвестиций. Надеюсь, это руководство помогло вам лучше понять, как оно работает, почему оно используется, а также плюсы и минусы.
CFI является официальным поставщиком программы сертификации Financial Modeling & Valuation Analyst® Станьте сертифицированным аналитиком финансового моделирования и оценки (FMVA) ® Сертификация CFI по финансовому моделированию и оценке (FMVA) ® поможет вам обрести уверенность в своих финансах. карьера. Запишитесь сегодня !. Чтобы продолжить карьеру, ознакомьтесь с соответствующими ресурсами:
- Руководство по финансовому моделированию Что такое финансовое моделирование Финансовое моделирование выполняется в Excel для прогнозирования финансовых показателей компании.Обзор того, что такое финансовое моделирование, как и зачем его создавать.
- Лучшие практики финансового моделирования Передовые методы финансового моделирования Эта статья предоставляет читателям информацию о передовых методах финансового моделирования и простое пошаговое руководство по построению финансовой модели.
- Расширенные формулы Excel Расширенные формулы Excel, которые необходимо знатьЭти расширенные формулы Excel очень важно знать и выведут ваши навыки финансового анализа на новый уровень. Загрузите нашу бесплатную электронную книгу Excel!
- Все статьи об оценке Оценка Оценка относится к процессу определения текущей стоимости компании или актива.Это можно сделать с помощью ряда техник. Аналитики, которые хотят
Как рассчитать чистую приведенную стоимость (NPV)
Когда дело доходит до оценки инвестиций, может быть очень полезно знать, как рассчитать чистую приведенную стоимость. Узнайте, что именно вы можете узнать из чистой приведенной стоимости, и получите краткую информацию о лучших формулах чистой приведенной стоимости для использования в своем бизнесе.
Что такое ЧПС?
Чистая приведенная стоимость — это разница между текущей стоимостью ваших денежных поступлений и текущей стоимостью ваших денежных оттоков за определенный период.Он используется в планировании инвестиций и составлении бюджета капиталовложений для измерения рентабельности проектов или инвестиций, аналогично учетной норме доходности (ARR). По сути, глядя на все деньги, которые вы ожидаете получить от инвестиций, и переводя эту прибыль в долларовую стоимость сегодняшнего дня, вы можете определить, стоит ли конкретное вложение.
Преимущества NPV
Ключевым преимуществом NPV является тот факт, что он учитывает временную стоимость денег (TVM), переводя будущие денежные потоки в стоимость сегодняшних долларов.Поскольку инфляция может подорвать покупательную способность, NPV обеспечивает гораздо более полезную меру потенциальной прибыльности вашего проекта. Кроме того, формулы чистой приведенной стоимости предоставляют единое четкое число, которое менеджеры могут сравнить с начальными инвестициями, чтобы определить успех проекта или инвестиции.
Какова формула чистой приведенной стоимости?
Научиться рассчитывать чистую приведенную стоимость относительно несложно, хотя важно помнить, что формула может варьироваться в зависимости от последовательности и количества денежных потоков, с которыми вы имеете дело.Если проект имеет только один денежный поток, вы можете использовать следующую формулу чистой приведенной стоимости для расчета NPV:
NPV = денежный поток / (1 + i) t — первоначальные инвестиции
В этом случае i = требуемая доходность или скидка скорость и t = количество периодов времени.
Если вы имеете дело с более длительным проектом, который включает в себя несколько денежных потоков, вам нужно будет использовать немного другую формулу чистой приведенной стоимости. Тем не менее, все это относительно абстрактно, поэтому, если вам нужен простой способ думать о формулах чистой приведенной стоимости, просто рассмотрите следующее:
NPV = сегодняшняя стоимость ожидаемых денежных потоков — сегодняшняя стоимость инвестированных денежных средств
Если вы закончите с положительной чистой приведенной стоимостью это означает, что прогнозируемая прибыль превышает ваши ожидаемые затраты, и инвестиции, вероятно, будут прибыльными.С другой стороны, инвестиция, которая приводит к отрицательной чистой приведенной стоимости, может привести к убыткам. Итак, если вы пытаетесь решить, стоит ли продолжать инвестировать, как правило, неплохо сосредоточиться только на проектах, которые предлагают положительную чистую приведенную стоимость.
Конечно, нет причин рассчитывать NPV самостоятельно, тем более, что существует множество калькуляторов NPV, которые можно использовать вместо этого. Investopedia предоставляет простой калькулятор NPV, который вы можете использовать для определения разницы между стоимостью ваших денежных поступлений и денежных потоков.
Рентабельность инвестиций в сравнении с чистой приведенной стоимостью
Рентабельность инвестиций (ROI) и чистая приведенная стоимость (NPV) — это оба метода оценки потенциальной прибыльности инвестиций. Но в чем разница между ними? Рентабельность инвестиций представляет собой чистую стоимость, которую вы получите от инвестиций за определенный период. Формула ROI выглядит следующим образом:
ROI = (Общая выгода — общие затраты) / общие затраты
Это очень просто и легко использовать, но из-за того, что это так просто, возможно, что ROI не говорит всей истории.Что еще важнее, ROI не учитывает временную стоимость денег, что делает ее несколько менее эффективной формой измерения, поскольку «будущие деньги» могут быть менее ценными, чем «настоящие деньги».
Когда дело доходит до ROI и NPV, важно помнить, что NPV — гораздо более сложное уравнение. Он уделяет гораздо больше внимания тому, когда возникают затраты и выгоды, прежде чем преобразовывать их в сегодняшние ценности. Поскольку NPV учитывает временную стоимость денег, она дает более глубокое представление о жизнеспособности ваших инвестиционных вариантов.
Мы можем помочь
GoCardless поможет вам автоматизировать сбор платежей, сократив количество администраторов, с которыми ваша команда должна иметь дело при поиске счетов. Узнайте, как GoCardless может помочь вам со специальными или регулярными платежами.
Эта статья показалась вам интересной? Узнайте, как рассчитать стоимость под риском (VaR)
GoCardless используется более чем 60 000 предприятий по всему миру. Узнайте больше о том, как вы можете улучшить обработку платежей в своем бизнесе уже сегодня.
Узнать больше Зарегистрироваться
Калькулятор чистой приведенной стоимости
Чистая приведенная стоимость (NPV) — это текущая стоимость всех будущих денежных потоков по проекту. Поскольку временная стоимость денег диктует, что деньги сейчас стоят больше, чем в будущем, стоимость проекта — это не просто сумма всех будущих денежных потоков. Эти будущие денежные потоки необходимо дисконтировать, потому что деньги, заработанные в будущем, сегодня меньше стоят. Чтобы рассчитать NPV, мы должны дисконтировать каждый будущий денежный поток, чтобы получить текущую стоимость каждого денежного потока, а затем суммировать эти текущие значения, связанные с каждым периодом времени.
Где:
- C = Денежный поток в момент времени t
- r = ставка дисконтирования в десятичном виде
- t = период времени
Вы можете думать о NPV по-разному, но я думаю, что проще всего думать о ней как о сумме приведенной стоимости всех денежных поступлений, то есть денежных средств, которые вы зарабатываете от проекта, за вычетом приведенной стоимости всех денежных оттоков, т.е. денежные средства, которые вы тратите на проект. Такой подход к NPV разбивает его на две части, но формула учитывает обе эти части одновременно.Приведенная стоимость рассчитывается с помощью нашей ставки дисконтирования r, которая представляет собой норму прибыли, которую мы могли бы ожидать от альтернативных проектов. Скажем, у вас есть доллар. Если вы не вложите этот доллар, в следующем году у вас все равно будет та же долларовая купюра; однако, если вы их инвестируете, через год у вас может быть больше этого доллара. Альтернативный проект — это инвестирование в долларах, а норма прибыли для этого альтернативного проекта — это скорость роста вашего доллара за один год.
Просто интуитивно подумав о стоимости денег во времени, если у вас есть временной ряд идентичных денежных потоков, денежный поток в первом периоде времени будет наиболее ценным, денежный поток во втором периоде времени будет второй по ценности и так далее. Это означает, что текущая стоимость денежных потоков уменьшается. Но это не всегда так, поскольку денежные потоки обычно изменчивы; однако мы все равно должны учитывать время. Мы делаем это с помощью ставки дисконтирования r, и каждый денежный поток дисконтируется на количество периодов времени, в течение которых денежный поток отличается от текущей даты.Это означает, что наш денежный поток за первый период проекта будет дисконтирован один раз, денежный поток во втором временном периоде будет дисконтирован дважды, и так далее. Чтобы дисконтировать денежный поток, просто разделите денежный поток на единицу плюс ставка дисконтирования, увеличенная до количества периодов, которые вы дисконтируете. Эта методология следует из сложных процентов. Давайте посмотрим на пример.
Пример
Предположим, вы, как инвестор, собираетесь вложить средства в проект для своей компании, который предоставит вам право собственности на новое оборудование, которое может помочь вашему бизнесу более эффективно производить виджеты.Это новое оборудование стоит 500 000 долларов за трехлетнюю аренду, но вы надеетесь, что благодаря этой новой машине ваша компания будет работать более эффективно и генерировать более высокие денежные потоки. Эта машина работает иначе, чем та, которую ваша компания в настоящее время использует для производства виджетов, поэтому вашим сотрудникам может потребоваться время, чтобы привыкнуть к работе с новым оборудованием. Таким образом, вы ожидаете, что денежные потоки со временем будут увеличиваться по мере того, как ваши сотрудники лучше знакомятся с оборудованием. По прогнозам ваших аналитиков, новая машина будет приносить денежные потоки в размере 210 000 долларов в первый год, 237 тысяч долларов во второй год и 265 тысяч долларов в третий год.Доходность альтернативного проекта — 6%. Какова чистая приведенная стоимость ваших потенциальных инвестиций?
Обычно проще всего просмотреть и настроить расчет, просмотрев таблицу денежных потоков. Вы можете подумать о создании таблицы для этого проекта, которая будет выглядеть примерно так, как показано ниже:
Оценить 0,06 Год 0 1 2 3 CF $ (500 000) 210 000 долл. США 237 000 долл. США 265 000 долл. США Наша ставка составляет 6%, и вы можете видеть ниже каждый год и денежный поток, связанный с этим годом.Помните, что в момент времени 0 (в настоящее время) вы должны потратить 500 000 долларов, чтобы получить новое оборудование. В следующие годы вы получите больше денег за счет увеличения производства виджетов. Теперь, когда у нас есть хорошее представление о финансовом состоянии проекта, приступим к расчету чистой приведенной стоимости.
Мы дисконтируем наш первый денежный поток, а точнее отток денежных средств, на нулевой год. Это просто означает, что мы действительно не дисконтируем первый денежный поток, потому что вы будете платить за проект в настоящее время, поэтому приведенная стоимость первого денежного потока — это просто первый денежный поток по номинальной стоимости.Остальные денежные потоки необходимо будет дисконтировать на количество лет, связанных с каждым денежным потоком. Мы дисконтируем наш денежный поток, заработанный в первом году, один раз, наш денежный поток, заработанный во втором году, дважды и наш денежный поток, заработанный в третьем году, трижды. После того, как мы вычислим текущую стоимость каждого денежного потока, мы можем просто суммировать их, поскольку каждый денежный поток скорректирован по времени на сегодняшний день. Суммируя денежные потоки, мы получаем чистую приведенную стоимость проекта. В этом случае наша чистая приведенная стоимость положительна, что означает, что проект стоит усилий.Однако будьте осторожны, поскольку прогнозируемые денежные потоки обычно являются оценочными, как и ставка дисконтирования. Наш окончательный расчет настолько хорош, насколько хорош его исходные данные.
Чистая приведенная стоимость как метод планирования капиталовложений
Компании часто используют чистую приведенную стоимость в качестве метода составления бюджета капиталовложений, потому что это, пожалуй, самый проницательный и полезный метод оценки целесообразности инвестирования в новый капитальный проект. Он более точен как с математической точки зрения, так и с точки зрения оценки стоимости денег во времени, чем методы периода окупаемости или дисконтированного периода окупаемости.Кроме того, в некоторых отношениях он более информативен, чем расчет индекса рентабельности или внутренней нормы прибыли.
Что такое чистая приведенная стоимость?
Чистая приведенная стоимость — это один из многих методов составления бюджета капиталовложений, используемых для оценки потенциальных проектов физических активов, в которые компания может пожелать инвестировать. Обычно эти проекты капитальных вложений крупны по объему и деньгам, например, покупка дорогостоящего сборочного оборудования или строительство нового здания.
Чистая приведенная стоимость использует в анализе дисконтированные денежные потоки, что делает чистую приведенную стоимость более точной, чем любой из методов капитального бюджета, поскольку он учитывает как переменные риска, так и временные переменные.
Анализ чистой приведенной стоимости включает несколько переменных и допущений и оценивает прогнозируемые денежные потоки, которые будут доставлены проектом, путем дисконтирования их до настоящего времени с использованием информации, которая включает временной промежуток проекта (t) и средневзвешенную стоимость капитала компании. (я).Если результат положительный, то фирме следует инвестировать в проект. В случае отрицательного результата фирма не должна вкладывать средства в проект.
Капитальные проекты с использованием чистой приведенной стоимости
Прежде чем вы сможете использовать чистую приведенную стоимость для оценки проекта капитальных вложений, вам необходимо знать, является ли этот проект взаимоисключающим или независимым. Независимые проекты — это проекты, на которые не влияют денежные потоки других проектов.
Однако взаимоисключающие проекты бывают разными.Если два проекта исключают друг друга, это означает, что есть два способа достижения одного и того же результата. Может случиться так, что компания запросила предложения по проекту, и было получено несколько предложений. Вы не захотите принимать две заявки на один и тот же проект. Это пример взаимоисключающего проекта.
Когда вы оцениваете два проекта капитальных вложений, вы должны оценить, являются ли они независимыми или взаимоисключающими, и с учетом этого принять решение о принятии или отклонении.
Правила принятия решений по чистой приведенной стоимости
Каждый метод капитального бюджета имеет набор правил принятия решений. Например, правило принятия решения метода периода окупаемости заключается в том, что вы принимаете проект, если он окупает свои первоначальные инвестиции в течение заданного периода времени. То же правило принятия решения справедливо и для метода дисконтированного срока окупаемости.
Чистая приведенная стоимость также имеет свои собственные правила принятия решений, которые включают следующее:
- Независимые проекты: Если NPV больше 0 долларов, принять проект.
- Взаимоисключающие проекты: Если ЧПС одного проекта больше ЧПС другого проекта, принять проект с более высокой ЧПС. Если оба проекта имеют отрицательную ЧПС, отклоните оба проекта.
Предположим, что фирма XYZ Inc. рассматривает два проекта, проект A и проект B, и хочет рассчитать NPV для каждого проекта.
- Проект A — это четырехлетний проект со следующими денежными потоками в каждый из четырех лет: 5000 долларов США, 4000 долларов США, 3000 долларов США, 1000 долларов США.
- Project B — это также четырехлетний проект со следующими денежными потоками в каждый из четырех лет: 1000 долларов США, 3000 долларов США, 4000 долларов США, 6750 долларов США.
- Стоимость капитала компании составляет 10 процентов для каждого проекта, а первоначальные инвестиции составляют 10 000 долларов.
Фирма хочет определить и сравнить чистую приведенную стоимость этих денежных потоков для обоих проектов. У каждого проекта неравномерное движение денежных средств. Другими словами, денежные потоки — это не аннуитеты.
Ниже приводится основное уравнение для расчета приведенной стоимости денежных потоков, NPV (p), , когда денежные потоки различаются в каждом периоде:
ЧПС (p) = CF (0) + CF (1) / (1 + i) t + CF (2) / (1 + i) t + CF (3) / (1 + i) t + CF (4 ) / (1 + i) т
Где:
- i = стоимость капитала фирмы
- t = год получения денежного потока
- CF (0) = начальные инвестиции
Чтобы работать по формуле NPV:
- Добавьте денежный поток из года 0, который является первоначальным вложением в проект, к остальным денежным потокам проекта.
- Первоначальная инвестиция — это отток денежных средств, поэтому это отрицательное число. В этом примере все денежные потоки для каждого проекта с 1 по 4 год являются положительными числами.
Совет: Вы можете расширить это уравнение на столько периодов времени, сколько длится проект.
Чтобы рассчитать NPV для проекта A:
NPV (A) = (- 10000 долларов) + 5000 долларов / (1,10) 1 + 4000 долларов / (1,10) 2 + 3000 долларов / (1,10) 3 + 1000 долларов / (1,10) 4
= 788 долларов.20
Чистая приведенная стоимость проекта A составляет 788,20 доллара, что означает, что если фирма инвестирует в проект, это добавляет 788,20 доллара к стоимости фирмы.
NPV Недостатки
Хотя NPV предлагает понимание и полезный способ количественной оценки стоимости проекта и потенциального вклада в прибыль, у него есть свои недостатки. Поскольку ни у одного аналитика нет хрустального шара, каждый метод составления бюджета капиталовложений страдает от риска неверно оцененных критически важных входных данных и предположений, а также от неожиданных или непредвиденных событий, которые могут повлиять на затраты и денежные потоки проекта.
Расчет NPV основывается на предполагаемых затратах, предполагаемой ставке дисконтирования и предполагаемой прогнозируемой доходности. Он также не может учитывать непредвиденные расходы, задержки во времени и любые другие проблемы, которые возникают на начальном или внутреннем этапе или во время проекта.
Кроме того, ставка дисконтирования и денежные потоки, используемые при расчете NPV, часто не охватывают все потенциальные риски, вместо этого предполагаются максимальные значения денежных потоков для каждого периода проекта. Это приводит к ложному чувству уверенности у инвесторов, и фирмы часто используют разные сценарии NPV, используя консервативные, агрессивные и наиболее вероятные наборы допущений, чтобы помочь снизить этот риск.
Альтернативные методы оценки
В некоторых случаях, особенно для краткосрочных проектов, имеют смысл более простые методы оценки. Метод срока окупаемости рассчитывает, сколько времени потребуется, чтобы окупить первоначальные инвестиции в проект. Несмотря на то, что он не учитывает прибыль, получаемую после возмещения первоначальных затрат, процессу принятия решения этот компонент анализа может не потребоваться. Этот метод имеет смысл только для краткосрочных проектов, поскольку он не учитывает временную стоимость денег, что делает его менее эффективным для многолетних проектов или в условиях инфляции.
Анализ внутренней нормы прибыли (IRR) — еще один часто используемый вариант, хотя он основан на той же формуле NPV. Анализ IRR отличается тем, что он учитывает только денежные потоки за каждый период и не принимает во внимание первоначальные инвестиции. Кроме того, результат получается путем вычисления ставки дисконтирования, а не путем вставки расчетной ставки, как в формуле NPV.
Результат формулы IRR рассчитан в годовом исчислении, что упрощает сравнение различных проектов.Формула NPV, с другой стороны, дает результат, который учитывает все годы проекта вместе, будь то один, три или более, что затрудняет сравнение с другими проектами с другими временными рамками.
- Определите количество периодов (t): Предполагается, что оборудование будет генерировать ежемесячный денежный поток и прослужит пять лет, что означает, что в расчет будет включено 60 денежных потоков и 60 периодов.{\ frac {1} {12}}) — 1 = 0,64 \%
Периодическая ставка = ((1 + 0,08) 121) -1 = 0,64%
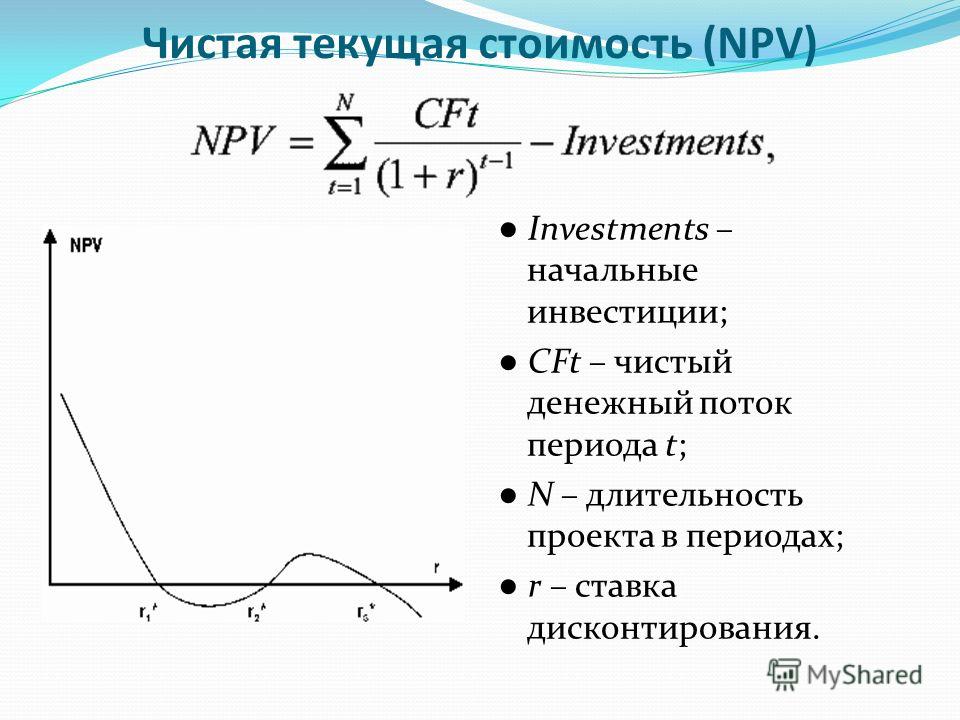 Значит платежи первого периода не надо дисконтировать, или следует считать, что номер этого периода — 0, т. к. (1+d) в нулевой степени равно 1, что как раз обеспечивает отсутствие дисконтирования.
Подход, при котором денежные потоки приходятся на начало периода, удобен в оценке инвестиционных проектов, — такие проекты часто начинаются с крупных расходов, которые не надо дисконтировать.
Значит платежи первого периода не надо дисконтировать, или следует считать, что номер этого периода — 0, т. к. (1+d) в нулевой степени равно 1, что как раз обеспечивает отсутствие дисконтирования.
Подход, при котором денежные потоки приходятся на начало периода, удобен в оценке инвестиционных проектов, — такие проекты часто начинаются с крупных расходов, которые не надо дисконтировать.


 Преимущество модели в возможности принимать во внимание степень эффективности и собственного, и заёмного капиталов. Помимо котировок обыкновенных акций, во внимание принимаются процентные ставки по заёмному капиталу.
Преимущество модели в возможности принимать во внимание степень эффективности и собственного, и заёмного капиталов. Помимо котировок обыкновенных акций, во внимание принимаются процентные ставки по заёмному капиталу.
Об авторе