Форма сзв м что это: сроки сдачи, заполнение, бланк новой формы и образец — Контур.Экстерн
С 30 мая действует новая форма отчета СЗВ-М для ПФР
Правление ПФР постановлением от 15 апреля 2021 года № 103п обновило форму отчета СЗВ-М («Сведения о застрахованных лицах»). Вступила в силу новая форма 30 мая 2021 года. Поэтому использовать ее работодатели должны уже при отправке отчетности за май.
Напомним, что СЗВ-М – это форма ежемесячной отчетности в ПФР, которую сдают все организации и ИП, имеющие наемных работников по трудовым договорам или договорам ГПХ, включая сотрудников, находящихся в декрете или отпуске, а также тех, с кем в отчетном месяце был расторгнут рабочий договор.
Сроки сдачи СЗВ-М – до 15-го числа месяца, следующего за отчетным. Так, отчет по новой форме СЗВ-М за май нужно сдать до 15 июня 2021 года.
Что изменилось в бумажной форме СЗВ-М
Существенно – ничего. Основных изменений три:
— Правила заполнения формы вынесены в отдельный порядок, что абсолютно ничего не меняет в вашей работе при заполнении формы.
— Тип формы теперь нужно прописывать полностью, вместо используемых ранее сокращений.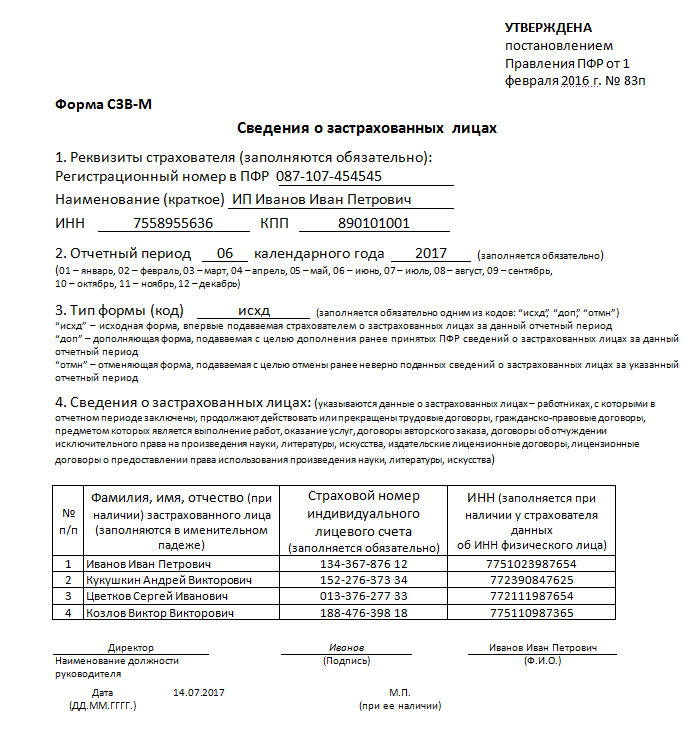 Например: «исходящая» вместо «исхд».
Например: «исходящая» вместо «исхд».
— Последнее скорее уточнение, а не изменение. СЗВ-М теперь нужно сдавать на директоров, являющихся единственными учредителями компании.
Что изменилось в электронной форме СЗВ-М
Ничего. Электронная форма СЗВ-М осталась неизменной. С порядком ее сдачи вы можете ознакомиться в постановлении Правления ПФР от 7 декабря 2016 года № 1077п.
Дело в том, что при отправке электронной формы часть изменений, внесенных в бумажный вариант, не будут иметь значения. Например, изменение об отмене сокращений не играет никакой роли для электронной СЗВ-М, так как в электронном варианте тип формы указывается с помощью кода, то есть его не нужно прописывать словами.
Отчетность в ПФР – без проблем с сервисами Такском
Форма отчета СЗВ-М максимально простая и не громоздкая, однако многие бухгалтеры и кадровики совершают ошибки при ее заполнении. А еще это одна из форм, по которой ежедневно выписывается наибольшее число штрафов.
Максимально минимизировать вероятность ошибки можно, используя сервисы для электронной отчетности. Тем более, что в электронной СЗВ-М, как мы уже сообщили, ничего не поменялось.
Во-первых, вам не придется следить за новостями об обновлениях – все формы отчетности, представленные в программных продуктах Такском, актуальны на сегодняшний день и отвечают последним изменениям законодательства.
Во-вторых, при заполнении форм отчетности вы видите текстовые подсказки по их заполнении – очень удобно, чтобы не обращаться за помощью к дополнительным интернет ресурсам.
В-третьих, во всех сервисах Такском для отчетности через интернет встроена автоматическая система проверки на ошибки, которая не даст вам отправить некорректно заполненный отчет или отчет с пропущенными полями.
Узнать подробнее о преимуществах электронной отчетности и подобрать тарифный план вы можете здесь.
Отправить
Запинить
Твитнуть
Поделиться
Поделиться
Новая форма СЗВ-М за май 2021
Оглавление СкрытьЧто изменилось в бланке
Новая форма СЗВ-М приведена в приложении № 1 к Постановлению Правления ПФ РФ № 103п от 15. 04.2021.
04.2021.
В разделе 1 «Реквизиты страхователя» вместо краткого наименования организации теперь можно написать полное или сокращённое.
В разделе 3 «Тип формы (код)» вместо сокращенных «исхд», «доп» или «отмн» нужно указывать полностью:
- «Исходная» — если сдаёте СЗВ-М за отчётный период (месяц) впервые;
- «Дополняющая» — если нужно дополнить ранее принятый фондом отчёт;
- «Отменяющая» — для отмены принятых ошибочных сведений.
Также из бланка убрали все пояснения к разделам. Их перенесли в отдельное приложение № 2 «Порядок заполнения формы СЗВ-М».
Как заполнить СЗВ-М с учётом изменений
Правила заполнения в целом не изменились, но есть нюансы.
- В строке «Полное или сокращённое наименование» вписывают название организации как в учредительных документах. Оно может быть и на латинице.
- В разделе 4 «Сведения о застрахованных лицах» фамилию, имя, отчество работников заполняют в именительном падеже.
 Нельзя ничего сокращать и писать инициалы.
Нельзя ничего сокращать и писать инициалы. - В графе «№ п/п» нумерация должна быть сквозной — по возрастанию без пропусков и повторов (1, 2, 3, 4 и т. д.).
- 11-значный СНИЛС заполняют в формате XXX–XXX–XXX–CC или XXX–XXX–XXX CC.
- ИНН работника заполняют, если у работодателя есть эта информация. Если нет, графу оставляют пустой.
В порядке заполнения теперь чётко прописано, что в СЗВ-М нужно включать застрахованных лиц, на которых распространяется обязательное пенсионное страхование согласно ст. 7 закона № 167-ФЗ от 15 декабря 2001 г. Это значит, что заполнить СЗВ-М нужно и на руководителя организации — единственного учредителя, даже если с ним нет трудового договора. В старом бланке было только пояснение о том, что включать в отчёт нужно тех, с кем заключены трудовые или гражданско-правовые договоры.
Образец заполнения новой формы СЗВ-М
Образец заполнения новой формы СЗВ-М
Ответы на частые вопросы про заполнение СЗВ-М
Нужно ли заполнять СЗВ-М на работников, которым не начисляли и не выплачивали зарплату
Если в организации или у ИП числятся работники, их нужно включить в СЗВ-М, даже если за отчётный месяц не было начислений, выплаты зарплаты и уплаты страховых взносов. Главное, что с физлицом заключён трудовой или гражданско-правовой договор, который действовал хотя бы один день.
Главное, что с физлицом заключён трудовой или гражданско-правовой договор, который действовал хотя бы один день.
Как заполнить СЗВ-М, если нет работников, а есть директор без зарплаты
Если нет наёмных сотрудников, СЗВ-М сдают на директора — единственного учредителя. Даже если он работает без трудового договора и зарплаты, то всё равно состоит с организацией в трудовых отношениях. То есть считается застрахованным лицом в системе ОПС и на него тоже подают сведения по форме СЗВ-М (п. 14 Порядка заполнения).
Можно ли сдать СЗВ-М раньше окончания месяца
Последний день подачи формы СЗВ-М — 15-ое число месяца, следующего за отчётным. Но в законодательстве нет запрета сдавать её досрочно. То есть СЗВ-М за июнь можно сдать в этом же месяце, не дожидаясь его окончания.
Но после досрочной сдачи могут появиться новые сведения. Например, до окончания месяца приняли нового сотрудника. Тогда информацию в принятом отчёте придётся уточнить и подать СЗВ-М с типом формы «Дополняющая». Сделать это нужно до истечения срока сдачи отчёта.
Сделать это нужно до истечения срока сдачи отчёта.
Как заполнить дополняющую форму СЗВ-М
В разделе 3 «Тип формы (код)» нужно написать «Дополняющая». Реквизиты и отчётный период заполняют как в уже принятой исходной СЗВ-М. В дополняющую форму не нужно переносить информацию из исходного отчёта. Вносите только данные на сотрудников, которых недостаёт в первом отчёте.
СЗВ-ТД и СЗВ-M за май 2021
СЗВ-М и СЗВ-ТД — это два отчёта, подавать которые нужно ежемесячно. Отчёт СЗВ-М за май 2021 года заполняется уже по новой форме, а новый бланк СЗВ-ТД начинается действовать с июля 2021 года. Разберёмся в изменениях, которым подверглись оба ежемесячных отчёта.СЗВ-М
Общие сведения о форме и обзор изменений
СЗВ-М — документ, в котором представлены сведения о застрахованных лицах. Подавать отчёт по итогам месяца должны все страхователи: организации (в т. ч. иностранные, которые работают в России), индивидуальные предприниматели, а также адвокаты, частные детективы и нотариусы.
ч. иностранные, которые работают в России), индивидуальные предприниматели, а также адвокаты, частные детективы и нотариусы.
Исключение: индивидуальные предприниматели, адвокаты, частные детективы и нотариусы могут не сдавать СЗВ-М, если у них нет наёмных сотрудников и подрядчиков.
Изначально форму утвердили ещё в 2016 году, последний раз в таком виде её подавали за апрель 2021 года. С 30 мая этого года начинает действовать новая форма (Постановление Правления ПФ РФ от 15.04.2021 N 103п), и подавать за этот месяц её нужно уже в июне.
Смысл документа остался нетронутым, изменился только внешний вид бланка. В предыдущем Постановлении (№ 83п от 01.02.2016), которое утвердило уже прежнюю форму отчёта, не было пояснений по его заполнению, — они были представлены непосредственно в самом бланке. Главным нововведением в форму стало исключение этой информации из документа, а порядок заполнения привели в Приложении 1 к Постановлению.
Важно: теперь при заполнении графы «Тип формы (Код)» писать её название нужно полностью, а не сокращённо, как было принято в старом бланке.
Порядок заполнения отчёта, приведённый в Постановлении, подробнее, чем пояснения, которые раньше давались в самом бланке. Он помогает разобраться с некоторыми вопросами, например, теперь можно с уверенностью сказать, что директоров-единственных учредителей включать в документ нужно обязательно. Раньше этот момент был под вопросом.
Заполнение формы и образец
Сдать СЗВ-М можно в электронном формате или на бумажном носителе до 15 числа месяца, следующего за отчётным. СЗВ-М за май 2021 года нужно сдать до 15 июня.
Важно: если количество физических лиц, включённых в отчёт, равно или превышает 25 человек, отчёт нужно подавать исключительно в электронном виде и подписывать его квалифицированной электронной подписью.Сам отчёт СЗВ-М состоит из четырёх разделов:
Реквизиты страхователя. В этом разделе нужно указать регистрационный номер в ПФР, полное или сокращённое название организации, а также ИНН и КПП.
Отчётный период календарного года.

Тип формы (код). Заполнить эту строку нужно в соответствии с той формой, которая подаётся: «Исходная», «Дополняющая» или «Отменяющая».
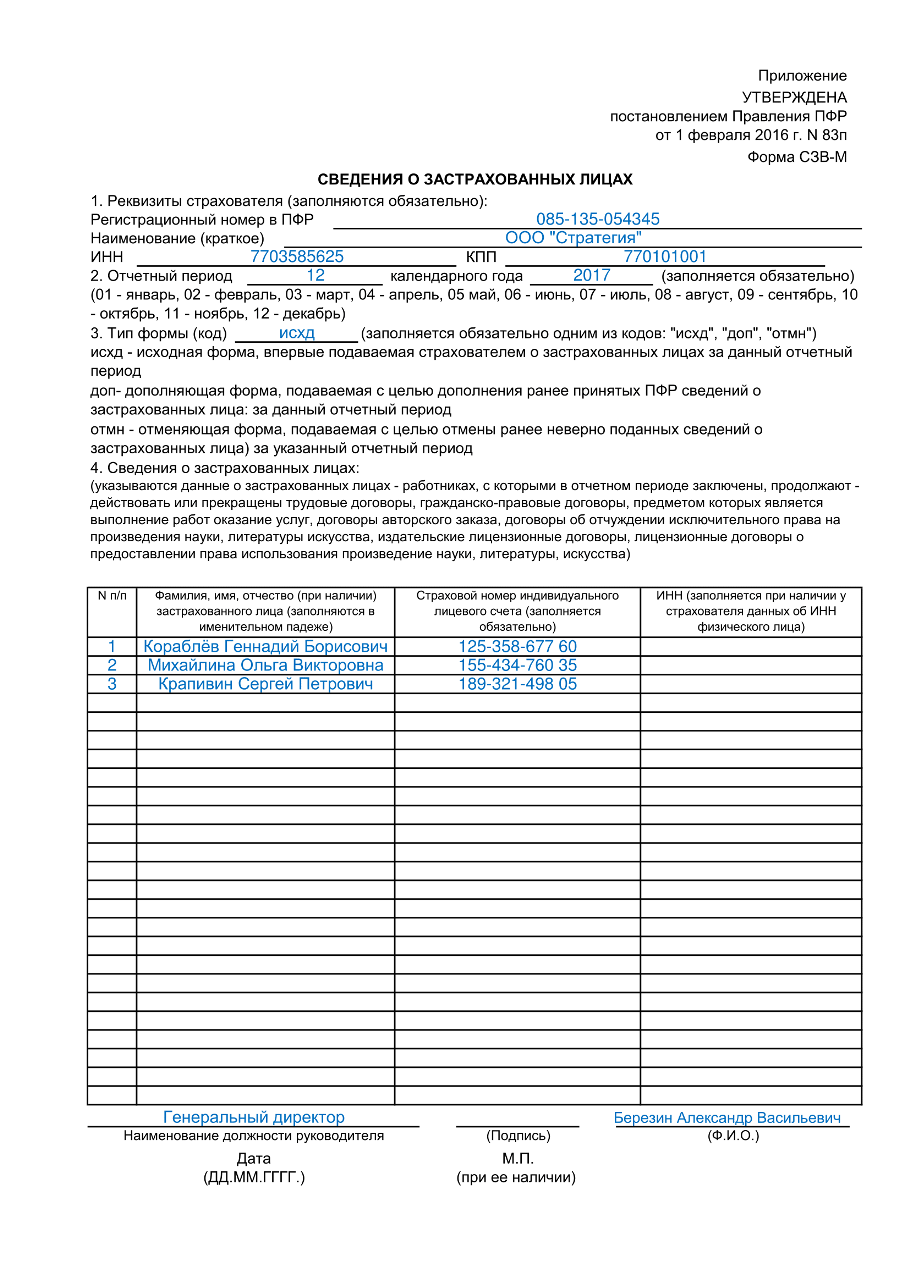
Сведения о застрахованных лицах. В таблицу нужно вписать всех работников, на которых распространяется обязательное пенсионное страхование. На каждое застрахованное лицо должно быть заполнено его Ф.И.О., СНИЛС и ИНН. № п/п указывается в порядке возрастания.
Внизу бланка нужно поставить подпись и Ф.И.О. заполнившего документ, а также написать название должности руководителя и дату заполнения. При наличии, нужно поставить печать.
Бланк СЗВ-М с мая 2021 года выглядит следующим образом:
СЗВ-ТД
Общие сведения о форме
СЗВ-ТД — документ, в котором представлены сведения о трудовой деятельности застрахованных лиц. С января 2020 года отчёт подают все работодатели, у которых есть работники, даже если работник всего один.
Сведения о трудовой деятельности — это аналог трудовой книжки, представленный в электронном формате. Сдавать отчёт нужно только по тем сотрудникам, статус которых в отчётный период изменился. К таким изменениям относят:
приём на работу;
увольнение;
изменения названия страхователя;
установление страхователю новой профессии, специальности или квалификации;
перевод на другую работу;
запрет на занятие должности;
подача заявление о выборе трудовой книжки (электронный или бумажный формат).
Исходя из этого следует, что подавать нулевой отчёт не нужно. То есть если за отчётный месяц ни у одного из работников не изменился статус, подавать пустой бланк в таком случае не требуется.
Какие изменения будут с июля
Новая форма СЗВ-ТД утверждена Постановлением Правления ПФ РФ № 769п от 27 октября 2020 года. Её положения вступают в силу 1 июля 2021 года, следовательно, на новом бланке сведения о застрахованных лицах нужно подавать уже за июнь, а за май — на прежнем.
Её положения вступают в силу 1 июля 2021 года, следовательно, на новом бланке сведения о застрахованных лицах нужно подавать уже за июнь, а за май — на прежнем.
Итак, в форму СЗВ-ТД внесли следующие изменения:
Добавили раздел «Сведения о работодателе, правопреемником которого является страхователь».
В табличную часть добавили пункт «Работа в районах Крайнего Севера или местностях, приравненных к районам Крайнего Севера».
Изменили графу «Код выполняемой функции» и пересмотрели порядок её заполнения.
Заполнение формы и образец
Как и в случае с СЗВ-М, СЗВ-ТД нужно подавать в электронном виде, если у работодателя больше 24 работников. Если работников 24 и меньше, то подавать документ он имеет право и на бумажном носителе.
Чтобы подать документ в электронном виде, нужна квалифицированная электронная подпись. Для этой цели подойдёт «Астрал-ЭТ», кроме того, её можно использовать для регистрации онлайн-кассы, работы на госпорталах и участия в торгах.
Ещё одно сходство с документом, о котором мы говорили в прошлом разделе, это дата подачи. СЗВ-ТД подаётся ежемесячно до 15 числа, то есть за май документ нужно подать до 15 июня.
Рассмотрим порядок заполнения бланка.
Сведения о страхователе. В этом разделе необходимо указать наименование организации в соответствии с учредительными документами, ИНН, КПП, а также регистрационный номер в ПФР.
Сведения о работодателе, правопреемником которого является страхователь.
Сведения о зарегистрированном лице. В отведённых графах нужно указать Ф.И.О. зарегистрированного лица, его дату рождения и СНИЛС.
Сведения о дате подачи заявления. Здесь нужно заполнить одну из строк в зависимости от того, предоставляются ли сведения о трудовой деятельности или продолжается их ведение.
 Могут быть заполнены обе строки, но даты в них должны стоять разные.
Могут быть заполнены обе строки, но даты в них должны стоять разные.Табличная часть. По порядку заполняются все графы таблицы, подробно остановимся только на тех графах, где произошли изменения. В графе «Работа в районах Крайнего Севера или местностях, приравненных к районам Крайнего Севера» при необходимости нужно указать код РКС или МКС соответственно. В графе «Код выполняемой функции» указывается кодовое обозначение занятия в соответствии с занимаемой должностью по ОКЗ (Общероссийский классификатор занятий).
Внизу нужно поставить подпись и Ф.И.О. заполнившего документ, а также написать название должности руководителя и дату заполнения. При наличии, нужно поставить печать.
Сам бланк СЗВ-ТД с июля 2021 года будет выглядеть следующим образом:
СЗВ-М и СЗВ-ТД удобно заполнять в веб-сервисе «Астрал Отчёт 5.0». Все типы отчётов всегда имеют актуальную версию.Как сдать отчет по форме СЗВ-М?
Получать статьи на почту
Подключите сервис 1С-Отчетность бесплатно на 30 дней!
Шаг 1. Открытие раздела Документы персучета
В программе 1С заходим во вкладку Отчетность, справки и выбираем Документы персучета.
Рис. 1. Вкладка Отчетность, справки в 1С: ЗУП ред. 3.1
Шаг 2. Создание отчета по форме СЗВ-М
В отрывшемся разделе Документы персучета нажимаем на кнопку Создать и выбираем Сведения о застрахованных лицах, СЗВ-М.
Рис. 2. Раздел Документы персучета
Шаг 3. Заполнение отчета по форме СЗВ-М
В отчете выбираем отчетный период и тип формы «Исходная». Нажимаем кнопку Заполнить.
Рис. 3. Заполнение отчета о застрахованных лицах
3. Заполнение отчета о застрахованных лицах
Шаг 4. Проверка корректности заполнения отчета
Сервис позволяет запустить программу, проверяющую корректность заполнения отчета.
На кнопке Отправить нажмите на стрелку вниз и выберите Проверить в Интернете.
Рис. 4. Проверка корректности заполнения отчета
В открывшемся окне заполните согласие на передачу персональных данных и нажмите Продолжить.
Рис. 5. Форма согласия на передачу персональных данных
По итогам проверки отчета программа выдаст сообщение. Если ошибок в отчете не обнаружено, переходите к следующему шагу.
Рис. 6. Сообщение об отсутствии ошибок в отчете
Шаг 5. Отправка отчета в Пенсионный фонд РФ
На кнопке Отправить нажмите на стрелку вниз и выберите Отправить в ПФР.
Рис. 7. Отправка отчета в ПФР
Подтвердите, что отчет заполнен полностью и корректно, нажмите отправить.
Рис. 8. Подтверждение отправки отчета
Далее вы увидите сообщение о том, что отчет успешно отправлен в ПФР.
Рис. 9. Сообщение о сдаче отчета
Шаг 6. Проверка отправки отчета
Для того чтобы проверить отправку отчета в разделе Отчетность, справки, зайдите в раздел 1С-Отчетность.
Рис. 10. Вкладка Отчетность, справки в 1С: ЗУП ред. 3.1
В разделе Отчеты можно увидеть отправленные в контролирующие органы документы и их статус. Отчет по форме СЗВ-М сразу после отправки будет иметь статус Отправлено в ПФР.
Рис. 11. Вкладка Отчеты в разделе 1С-Отчетность
После обновления информации с контролирующими органами статус отчета должен измениться на Отчет успешно сдан.
С сервисом 1С-Отчетность сдать отчет просто и удобно. Вы можете оформить у нас бесплатный доступ на месяц к сервису, для того чтобы попробовать в работе все преимущества.
Подключите сервис бесплатно на 30 дней!
Ответы на часто возникающие вопросы
Когда сдавать отчет
Отчет о застрахованных лицах необходимо сдавать до 15-го числа месяца, следующего за отчетным.
Кому нужно сдавать отчет
Всем организациям и ИП, имеющим в найме сотрудников по трудовому и гражданско-правовому договору, необходимо подавать в ПФР сведения о застрахованных лицах.
В отчет должны включаться сотрудники в декрете, отпуске и уволившиеся в рамках отчетного периода.
Можно ли сдавать отчет досрочно
Отчет можно сдать с 1-го числа месяца, следующего за отчетным.
Как исправить ошибку в отчете
Чтобы исправить ошибку в сведениях отчета по форме СЗВ-М, необходимо заполнить и отправить дополняющую/отменяющую форму.
Остались вопросы?
Наши специалисты свяжутся с вами, чтобы уточнить подробности!
| Ошибка | Действия плательщика |
| Ошибка при заполнении кода отчетного периода (месяц или год) — например, 09 (сентябрь) вместо 08 (август). | В данном случае организация получает положительный протокол, при этом отчетность за 08 (август) фактически не считается сданной. Следует представить исходную форму за 08 (август). За 09 (сентябрь) форма уже считается принятой, при необходимости за сентябрь может быть представлена дополняющая форма (при наличии новых работников), или отменяющая форма (если есть ошибочно включенные работники). |
Ошибка структуры файла: Файл не соответствует xsd-схеме. | В данном случае организации придет отрицательный протокол. Следует представить Исходную форму. |
| Ошибка на дубликат: При предоставлении сведений о застрахованных лицах с типом формы «Исходная» не должно быть ранее представленных сведений с типом «Исходные» за отчетный период, за который представляются сведения. | В данном случае организации придет отрицательный протокол. Данный протокол говорит, что «Исходная» форма предприятием уже представлялась, следовательно, необходимо представлять форму СЗВ-М «Дополняющую». |
| Ошибка регистрационного номера в ПФР и наименования страхователя: Элемент «Регистрационный номер». Указывается номер, под которым страхователь зарегистрирован как плательщик страховых взносов, с указанием кодов региона и района по классификации, принятой в ПФР. | В случае некорректного заполнения организации придет отрицательный протокол. Следует представить «Исходную» форму. |
| Ошибка ФИО, СНИЛС и ИНН: 1. Отсутствие элементов «Фамилия», «Имя», «Отчество»; 2. Указывается ФИО, содержащиеся в страховом свидетельстве; 3. Должен быть указан хотя бы один из элементов ‘Фамилия’ или ‘Имя’; 4. Во всех документах в элементах Фамилия, Имя, Отчество: не допускается смешение в этих элементах букв русского и латинского алфавитов; 5. Во всех документах в элементах Фамилия, Имя, Отчество знаки ‘–’ не могут идти подряд или через пробел; 6. Указывается СНИЛС, содержащийся в страховом свидетельстве. | В этом случае организация получает положительный протокол, в котором заполнен раздел «Ошибки» и указана информация о некорректно представленных сведениях. На лиц, по которым надо внести изменения представляется «Дополняющая» форма СЗВ-М. |
ОПОРНЫЕ ВЕКТОРНЫЕ МАШИНЫ (СВМ).
 Введение: все, что вам нужно знать… | by Ajay Yadav
Введение: все, что вам нужно знать… | by Ajay YadavМашины опорных векторов, так называемые SVM, представляют собой контролируемый алгоритм обучения , который можно использовать для задач классификации и регрессии в качестве вспомогательной векторной классификации (SVC) и поддержки векторной регрессии (SVR). Он используется для меньшего набора данных, поскольку его обработка занимает слишком много времени. В этом наборе мы сосредоточимся на SVC.
SVM основан на идее поиска гиперплоскости, которая наилучшим образом разделяет функции на разные домены.
Рассмотрим следующую ситуацию:
Сталкер отправляет вам электронные письма, и теперь вы хотите разработать функцию (гиперплоскость), которая будет четко различать два случая, так что всякий раз, когда вы получаете электронное письмо от сталкера, оно будет классифицироваться как спам. На следующем рисунке показаны два случая, в которых нарисована гиперплоскость. Какой из них вы выберете и почему? Найдите минутку, чтобы проанализировать ситуацию ……
Думаю, вы бы выбрали инжир (а). Вы думали, почему вы выбрали инжир (а)? Потому что электронные письма на рис (а) четко классифицированы, и вы более уверены в этом, чем на рис (б). По сути, SVM состоит из идеи создания оптимальной гиперплоскости , которая четко классифицирует различные классы (в данном случае это двоичные классы).
Вы думали, почему вы выбрали инжир (а)? Потому что электронные письма на рис (а) четко классифицированы, и вы более уверены в этом, чем на рис (б). По сути, SVM состоит из идеи создания оптимальной гиперплоскости , которая четко классифицирует различные классы (в данном случае это двоичные классы).
Ближайшие к гиперплоскости точки называются опорными точками вектора , а расстояние между векторами от гиперплоскости называется полями .
Основная интуиция, которую следует здесь развить, состоит в том, что чем дальше точки SV от гиперплоскости, тем больше вероятность правильной классификации точек в их соответствующих регионах или классах. Точки SV очень важны при определении гиперплоскости, потому что, если положение векторов изменяется, положение гиперплоскости изменяется. Технически эта гиперплоскость также может называться , максимизирующая запас гиперплоскости .
В этом посте мы так долго обсуждали гиперплоскость, давайте объясним ее значение, прежде чем двигаться дальше.Гиперплоскость — это функция, которая используется для различения элементов. В 2-D функция, используемая для классификации между элементами, является линией, тогда как функция, используемая для классификации элементов в 3-D, называется плоскостью, аналогично функция, которая классифицирует точку в более высоком измерении, называется гиперплоскостью. Теперь, когда вы знаете о гиперплоскости, давайте вернемся к SVM.
Допустим, есть размеры «m»:
, таким образом, уравнение гиперплоскости в измерении «M» может быть задано как =
, где
Wi = векторы (W0, W1, W2, W3… Wm )
b = смещенный член (W0)
X = переменные.
Теперь,
Предположим, 3 гиперплоскости, а именно (π, π +, π−), такие, что «π +» параллельно «π», проходящему через опорные векторы на положительной стороне, а «π−» параллельно » π ‘, проходящий через опорные векторы на отрицательной стороне.
уравнения каждой гиперплоскости можно рассматривать как:
для точки X1:
Объяснение: когда точка X1 мы можем сказать, что эта точка лежит на гиперплоскости, и уравнение определяет, что произведение нашего фактического выхода и уравнение гиперплоскости равно 1, что означает, что точка правильно классифицируется в положительной области.
для точки X3:
Объяснение: когда точка X3 мы можем сказать, что эта точка находится далеко от гиперплоскости, и уравнение определяет, что произведение нашего фактического выхода и уравнения гиперплоскости больше 1, что означает, что точка правильно классифицирован в положительной области.
для точки X4:
Объяснение: когда точка X4, мы можем сказать, что эта точка лежит на гиперплоскости в отрицательной области, и уравнение определяет, что произведение нашего фактического выхода и уравнения гиперплоскости равно 1, что означает, что точка правильно отнесена к отрицательной области.
для точки X6:
Объяснение: когда точка X6, мы можем сказать, что эта точка находится далеко от гиперплоскости в отрицательной области, и уравнение определяет, что произведение нашего фактического выхода и уравнения гиперплоскости больше 1, что означает, что точка правильно отнесена к отрицательной области.
Давайте рассмотрим ограничения, которые не классифицируются:
для точки X7:
Объяснение: Когда Xi = 7, точка классифицируется неправильно, потому что для точки 7 wT + b будет меньше единицы, и это нарушает ограничения.Итак, мы обнаружили неправильную классификацию из-за нарушения ограничений. Точно так же мы можем сказать для точек Xi = 8.
Таким образом, из приведенных выше примеров мы можем сделать вывод, что для любой точки Xi,
, если Yi (WT * Xi + b) ≥ 1:
, тогда Си правильно классифицирован
иначе:
Си неправильно классифицирован.
Итак, мы можем видеть, что если точки линейно разделимы, то только наша гиперплоскость может различать их, а если вводится какой-либо выброс, то он не может их разделить.Таким образом, этот тип SVM называется как SVM с жестким запасом (поскольку у нас есть очень строгие ограничения для правильной классификации каждой точки данных).
Мы в основном считаем, что данные линейно разделимы, и это может быть не так в реальном сценарии. Нам нужно обновление, чтобы наша функция могла пропустить несколько выбросов и иметь возможность классифицировать почти линейно разделяемые точки. По этой причине мы вводим новую переменную Slack ( ξ), которая называется Xi.
, если мы введем ξ в наше предыдущее уравнение, мы можем переписать его как
Введение Xi, если ξi = 0,
точки можно считать правильно классифицированными.
иначе:
ξi> 0, неправильно классифицированные точки.
, поэтому, если ξi> 0, это означает, что Xi (переменные) находятся в неправильном измерении, поэтому мы можем думать о ξi как об ошибке, связанной с Xi (переменной).Средняя ошибка может быть выражена как;
средняя ошибка, таким образом, наша цель математически может быть описана как;
, где ξi = ςi
ЧТЕНИЕ: найти вектор w и скаляр b, такие, что гиперплоскость, представленная w и b, максимизирует запасное расстояние и минимизирует член потерь при условии, что все точки правильно классифицирован.
Эта формулировка называется методом мягких полей.
, когда Zi ≥ 1, тогда потери равны 0, когда Zi <1, тогда потери возрастают., таким образом, можно интерпретировать, что потери на шарнире являются максимальными (0,1-Zi).
Теперь давайте рассмотрим случай, когда наш набор данных вовсе не является линейно разделимым.
в основном, мы можем отделить каждую точку данных, проецируя ее в более высокое измерение, добавляя к ней соответствующие функции, как мы это делаем в логистической регрессии. Но с помощью SVM есть мощный способ выполнить эту задачу по проецированию данных в более высокое измерение. Обсуждаемая выше формулировка представляла собой первичную форму SVM .Альтернативный метод представляет собой двойную форму SVM, которая использует множитель Лагранжа для решения задачи оптимизации ограничений.
Примечание:
Если αi> 0, то Xi является опорным вектором, а когда αi = 0, то Xi не является опорным вектором.
Наблюдение:
- Для решения реальной проблемы нам не требуется фактическая точка данных, вместо этого может быть достаточно скалярного произведения между каждой парой вектора.
- Для вычисления смещенной константы «b» нам требуется только скалярное произведение.
- Основным преимуществом двойной формы SVM перед формулировкой Лагранжа является то, что она зависит только от α .
Переходя к основной части SVM, которой она наиболее известна, это трюк с ядром . Ядро — это способ вычисления скалярного произведения двух векторов x и y в некотором (очень многомерном) пространстве признаков, поэтому функции ядра иногда называют «обобщенным скалярным произведением».
попробуйте прочитать это уравнение… s.t = подчиненоПрименение трюка ядра означает просто замену скалярного произведения двух векторов функцией ядра.
- линейное ядро
- полиномиальное ядро
- ядро радиальной базисной функции (RBF) / гауссово ядро
Мы сосредоточимся на полиномиальном и гауссовском ядрах, поскольку они наиболее часто используются.
Ядро полинома:
В общем случае ядро полинома определяется как;
b = степень ядра & a = постоянный член.t и Zb.Метод 1:
Традиционно мы решаем эту проблему следующим образом:
, что потребует много времени, так как нам нужно будет выполнить скалярное произведение для каждой точки данных, а затем вычислить скалярное произведение, которое нам может потребоваться для умножения. Представьте, что мы делаем это для тысяч точек данных….
Или мы могли бы просто использовать
Method 2:
с использованием уловки ядра:
В этом методе мы можем просто вычислить скалярное произведение, увеличив значение мощности. Просто не правда ли?
Ядро радиальной базисной функции (RBF) / Гауссово ядро:
Гауссовское RBF (радиальная базисная функция) — еще один популярный метод ядра, используемый в моделях SVM для большего.Ядро RBF — это функция, значение которой зависит от расстояния от начала координат или от некоторой точки. Гауссовское ядро имеет следующий формат;
|| X1 — X2 || = Евклидово расстояние между X1 и X2Используя расстояние в исходном пространстве, мы вычисляем скалярное произведение (сходство) X1 и X2.
Примечание: сходство — это угловое расстояние между двумя точками.
Параметры:
- C: сила, обратная степени регуляризации.
Поведение: с увеличением значения «c» модель переобучается.
Поскольку значение «c» уменьшается, модель не соответствует требованиям.
2. γ: Гамма (используется только для ядра RBF)
Поведение: По мере увеличения значения « γ » модель становится переобученной.
Поскольку значение « γ » уменьшается, модель не подходит.
Плюсы:
- Это действительно эффективно в высшем измерении.
- Эффективно, когда количество функций больше, чем обучающих примеров.
- Лучший алгоритм, когда классы разделяются
- На гиперплоскость влияют только опорные векторы, поэтому выбросы имеют меньшее влияние.
- SVM подходит для двоичной классификации крайних случаев.
минусы:
- Для обработки большего набора данных требуется много времени.
- Плохо работает в случае перекрытия классов.
- Правильный выбор гиперпараметров SVM, обеспечивающий достаточную производительность обобщения.
- Выбор подходящей функции ядра может быть непростым.
SVM предполагает, что у вас есть входные данные числовые, а не категориальные. Таким образом, вы можете преобразовать их, используя один из наиболее часто используемых « one hot encodin g, label-encoding etc ».
2. Двоичное преобразование:Поскольку SVM может классифицировать только двоичные данные, вам нужно будет преобразовать многомерный набор данных в двоичную форму, используя ( один против остальных метод / один метод против одного ) метод преобразования.
SVM ДВОЙНОЙ РЕЦЕПТ. Машина опорных векторов (SVM) — это… | автор: sathvik chiramana
Машина опорных векторов (SVM) — это контролируемый алгоритм машинного обучения, который используется как для задач классификации, так и для задач регрессии, но используется в основном для классификации. В этом блоге мы в основном сосредоточимся на классификации и посмотрим, как работает svm внутри.
Прочитав эту статью, вы сможете получить представление о следующих концепциях
- Как работает SVM с?
- Что такое множитель Лагранжа и как он используется в SVM?
- Что такое двойной состав SVM?
Основная задача SVM :
Основная задача svm — найти лучшую разделяющую гиперплоскость для набора обучающих данных, которая максимизирует запас.
Здесь есть много гиперплоскостей, которые могут разделять два класса, и svm найдет гиперплоскость, максимизирующую маржу
Причина максимизации маржи гиперплоскости :
Чем меньше маржа, тем шансы ошибочной классификации точек. Если мы сохраним маржу как можно более широкой, мы уменьшим вероятность того, что положительные / отрицательные баллы будут неправильно классифицированы.
Математика SVM
Взято из обмена стекамиЗдесь плоскость гиперплоскости w`x + b = 0 — это центральная плоскость, которая разделяет положительные и отрицательные точки данных. w`x + b = 1 — это плоскость, над которой лежат положительные точки, а w`x + b = -1 — плоскость, ниже которой лежат все отрицательные точки.
Теперь запас — это расстояние между плоскостями w`x + b = 1 и w`x + b = -1 , и наша задача — максимизировать запас.
И мы можем обнаружить, что расстояние между этими двумя гиперплоскостями равно 2 / || w || (см. Это), и мы хотим максимизировать это расстояние
HARD MARGIN SVM:В жестком поле svm мы предполагаем, что все положительные точки лежат выше плоскости π (+), а все отрицательные точки лежат ниже плоскости π (-), и никакие точки не лежат между краями.Это можно записать как ограничение y_i * (w`x_i + b) ≥1
Теперь всю функцию оптимизации можно записать как
MAX (w) {2 / || w || } такое, что y_i * (w`x_i + b) ≥1MAX (w) {2 / || w || } можно записать как min (w) {|| w || / 2}, а также можно переписать как min (w) {|| w || ² / 2}
Как найти решение проблемы оптимизации с ограничениями?
В математической оптимизации метод множителей Лагранжа представляет собой стратегию нахождения локальных максимумов и минимумов функции с ограничениями равенства.2 → (1)
так, что h (x, y) = x + y − 1 = 0
, мы можем переписать ограничение как y = 1-x → (2)
Теперь нарисуйте уравнения (1) и (2) на том же графике, и он будет выглядеть примерно так.
Лагранж обнаружил, что минимум f (x, y) при ограничении g (x, y) = 0 получается , когда их градиенты указывают в одном направлении. . И из графика мы можем ясно видеть, что градиенты как f, так и g указывают почти в одном направлении в точке (0,5,0,5), и поэтому мы можем объявить, что f (x, y) минимален в точке (0.5,0.5) такой, что g (x, y) = 0
И мы можем записать это математически как
∇f (x, y) = λ∇g (x, y) ==> ∇f (x, y) -λ∇g (x, y) = 0
, где ∇ обозначает градиент, и мы умножаем градиент g на f, потому что градиенты f и g почти равны, но не в точности равны, поэтому, чтобы сделать их равными, мы вводим λ в этом уравнении, и это λ называется множителем лагранжа
Теперь вернемся к нашей проблеме жесткого запаса SVM, мы можем записать его в терминах лагранжа следующим образом:
, где альфа — множитель лагранжа
Двойная форма SVM
Проблема Лагранжа обычно решается с использованием двойственной формы.Принцип двойственности гласит, что оптимизацию можно рассматривать с двух разных точек зрения. Первая — это простая форма, которая представляет собой задачу минимизации, а другая — двойную задачу, которая является проблемой максимизации
Лагранжевая формулировка SVM:
Для решения задачи минимизации мы должны взять частную производную по w, а также b
Заменить все это в уравнении 7.1, тогда мы получаем
. Таким образом, окончательное уравнение будет
. Следующая задача оптимизации называется двойной задачей.
Почему мы пытаемся максимизировать лагранжиан в SVM?
Пусть p ∗ — оптимальное значение задачи минимизации || w || ² / 2 (прямое). Двойственная лагранжева функция обладает тем свойством, что L (w, b, α) ≤p ∗. Это нижняя граница основной функции. Вместо решения прямой задачи мы хотим получить максимальную нижнюю оценку p ∗, максимизируя двойственную функцию Лагранжа (двойственная проблема).
Soft Margin SVM
Идея здесь состоит в том, чтобы не делать нулевую ошибку классификации при обучении, а сделать несколько ошибок, если это необходимо. T.Xj)
Машина опорных векторов (SVM). Машина опорных векторов (SVM) — это… | автор: Акшай Чаван
Машина опорных векторов (SVM) — это управляемая модель машинного обучения (набор данных помечен). Это означает, что если у нас есть набор данных, чтобы попытаться запустить на нем SVM, мы часто получаем довольно хорошие результаты. Это потому, что он основан на сильной и красивой математической основе.Этот алгоритм используется как для классификации (SVC) , так и для регрессии (SVR) . В этом посте мы в основном сосредоточимся на классификации и рассмотрим основную идею SVM.
Прочитав эту статью, вы сможете ответить на следующие вопросы.
- Что такое SVM? Основная идея SVM
- Что такое маржа и как формируется задача оптимизации с ее ограничениями?
- Что такое ядро и как его уловка используется в SVM?
- Что такое ядро RBF?
Содержание:
1.Задача в SVM
2. Intuition
3. Возможная оптимальная гиперплоскость VS
4. Маржа
5. Вычисление наибольшей маржи
5.1 Понимание ограничений
5.2 Объединение 2 ограничений
6. Формула Лагранжа
7 Двойная форма SVM
8. Soft Margin SVM
9. Ядра
9.1 Что такое ядро?
10. Уловка ядра
11. Типы ядра
11.1 Линейное ядро
11.2 Полиномиальное ядро
11.3 Строковое ядро
12. Ядро радиальной базисной функции (RBF) / ядро Гаусса
13. Какое ядро использовать?
14. Интерпретация функции потерь SVM
15. SVM как регрессор (SVR)
16. Гиперпараметры и компромисс смещения и дисперсии
17. Сложность во времени и пространстве для SVM
18. Плюсы и минусы SVM
1. Задача в SVM:
Задача машины опорных векторов — найти лучшую разделяющую гиперплоскость (в более высоких измерениях) для обучающей выборки, которая максимизирует запас.
2. Интуиция:
Давайте рассмотрим следующую проблему:
В отделении неотложной помощи в больнице измеряются 2 переменных (например, артериальное давление и возраст) впервые поступивших пациентов. Необходимо принять решение о помещении пациента в отделение интенсивной терапии. Таким образом, проблема состоит в том, чтобы предсказать пациентов с высоким риском и отличить их от пациентов с низким риском. Распределение данных выглядит следующим образом:
Просто взглянув на график, мы интуитивно можем сказать, что лучшая гиперплоскость будет
. Такая линия называется разделяющей гиперплоскостью .
Хотя это всего лишь линия, но мы называем ее гиперплоскостью, потому что здесь мы рассматриваем только двухмерные данные, но SVM могут работать с любым количеством измерений. Линия в 2-D называется плоскостью в 3-D, и ее можно обобщить на гиперплоскость в более высоких измерениях.
3. Возможная оптимальная гиперплоскость VS:
Разделение гиперплоскости не означает, что это лучшая гиперплоскость. В примере, описанном выше, может быть несколько возможных гиперплоскостей, разделяющих данные, как показано ниже:
Рассматривая 1-ю гиперплоскость, мы можем ясно видеть, что один пациент высокого риска классифицирован неправильно.Таким образом, интуитивно мы можем сказать, что гиперплоскость, которая близка к точке данных, не может быть хорошо обобщена.
Итак, мы попытаемся выбрать гиперплоскость, которая находится как можно дальше от точек данных, которая называется Оптимальная гиперплоскость.
4. Маржа:
Учитывая гиперплоскость, мы вычисляем расстояние от гиперплоскости до ближайшей точки с обеих сторон, и то, что мы назвали это поле, составляет .
Глядя на рисунок интуитивно, мы можем сказать, что гиперплоскость рядом с точкой будет иметь меньший запас, а дальняя гиперплоскость от точки данных будет иметь больший запас.
Это причина того, что целью SVM является оптимальная гиперплоскость, которая максимизирует запас в обучающих данных.
5. Вычисление наибольшей маржи:
У нас есть данные, затем мы выбираем 2 гиперплоскости без точек между ними и максимизируем расстояние (маржу).
Допустим, у нас есть набор данных с Xi, связанным со значением yi. yi может принимать только 2 значения, то есть +1 и -1. Каждая точка данных в машинном обучении представлена как вектор m-размерности.
Более математически в терминах обозначений теории множеств мы можем написать:
Посмотрите на уравнение гиперплоскости,
, где
(где b — член смещения, такой же, как w0, отделенный)У нас есть гиперплоскость (π), разделяющая данные и удовлетворяет
Мы можем выбрать еще 2 гиперплоскости (π + и π-), которые будут иметь следующие уравнения соответственно.
иДля простоты рассмотрим p = 1
иМы хотим выбрать 2 гиперплоскости, которые будут удовлетворять следующим ограничениям.Для каждой точки данных
Для Xi, имеющего класс 1 Для Xi, имеющего класс -15.1 Понимание ограничений:
Когда Xi = A, мы видим, что точки находятся на гиперплоскости, поэтому wT + b = 1 и ограничения удовлетворены. Для всех точек над гиперплоскостью (π +) значение уравнения будет больше единицы (wT + b> 1). Поэтому нет никаких ошибок в классификации баллов, относящихся к положительному классу.
Когда Xi = B, мы видим, что точки находятся на гиперплоскости, поэтому wT + b = -1 и ограничения удовлетворяются.Для всех точек ниже гиперплоскости (π-) значение уравнения будет меньше единицы (wT + b <1). Таким образом, если ограничения соблюдены, то никакой ошибочной классификации не произойдет. Точки A и B называются опорными векторами .
Давайте посмотрим, в каких случаях ограничения не выполняются.
Когда Xi = C точка классифицируется неправильно, потому что для точки C wT + b будет меньше единицы, и сразу же ограничение нарушается. Итак, мы обнаружили неправильную классификацию из-за нарушения ограничений.Точно так же мы можем сказать и о точках D, E.
Путем определения ограничений мы нашли цель выбрать 2 гиперплоскости без точки между ними.
5.2 Объединение 2 ограничений:
Умножьте уравнение 5.2 на yi (которое всегда равно -1)
Умножьте уравнение 5.1 на yi (которое всегда равно 1)
Объедините уравнение 5.3 и 5.4,
расстояние между двумя гиперплоскостями представлено как:
Расстояние (d) между двумя гиперплоскостями можно вычислить,
В формуле мы можем изменить только одну переменную, это норма w
Если || w || = 1, то d = 2
Если || w || = 4, то d = 0.5
Если || w || = 10, тогда d = 0,2
Мы легко видим, что чем больше норма, тем меньше маржа. Наша цель — максимизировать маржу. Увеличение маржи — это то же самое, что минимизация нормы w.
Итак, наша задача оптимизации будет:
Свернуть в (w, b) || w ||
Решив ее, мы найдем пару w и b, для которых || w || самый маленький из возможных. Значит, у нас будет уравнение оптимальной гиперплоскости.
6.Формулировка Лагранжа:
Лагранж изобрел стратегию решения задачи оптимизации с учетом ограничений равенства. В нем говорится, что вы помещаете ваши ограничения в нулевую форму, умножаете их на ∝, называемое множителем лагранжа, и тогда это становится частью проблемы оптимизации.
Наша задача оптимизации:
При использовании функции лагранжа цель изменяется на
, где ∝i = множитель Лагранжа для каждой точки.
Коэффициент ½ был добавлен для удобства решателя Квадратичная задача (QP) для решения задачи, и возведение нормы в квадрат имеет еще одно преимущество: i.е удаление квадратного корня.
В приведенной выше формулировке интересно то, что мы одновременно минимизируем w.r.t w, b и максимизируем w.r.t ∝.
7. Двойная форма SVM:
Задача Лагранжа обычно решается с использованием двойной формы. Принцип двойственности гласит, что оптимизацию можно рассматривать с двух разных точек зрения. Первая точка зрения — это основная форма, которая представляет собой проблему минимизации, а другая точка зрения — двойная проблема, которая является для нас максимизацией.
Формулировка SVM Лагранжа:
Решение задачи минимизации означает взятие частной производной w.r.t w и b.
Подставьте все значения в уравнение 7.1, затем формулировка изменится на
В приведенном выше уравнении мы удалили w.
Таким образом, буква b также будет удалена.
Итак, задача оптимизации называется двойной задачей.
Основное преимущество двойной формы SVM перед формулировкой лагранжа состоит в том, что она зависит только от.
Все рецептуры, которые мы видели до сих пор, называются Hard Margin SVM . Это хорошо работает, когда данные линейно разделяются.
Но самая большая проблема в том, что реальные данные часто зашумлены. Так как же изменить проблему оптимизации в таких случаях?
Мы применяем следующую методику.
8. Soft Margin SVM:
Это модифицированная версия оригинальной SVM. Идея состоит в том, чтобы не допускать нулевой ошибки классификации при обучении, а сделать несколько ошибок, насколько это возможно. Таким образом, наши оптимизационные ограничения теперь принимают вид
, где ζi называется Zeta.Итак, задача оптимизации меняется на,
Добавление такого члена называется регуляризацией.Из-за чего мы сделаем минимально возможную ошибку с гиперплоскостью, которая максимизирует запас.
Приведенное выше уравнение можно минимизировать, добавив к нему отрицательные значения ζ. Поэтому мы устанавливаем другие ограничения, т.е. ζi больше или равно нулю.
Однако мы также должны контролировать мягкую маржу. Вот почему мы добавляем параметр C, который говорит нам, насколько важным должен быть ζ.
Таким образом, формулировка мягкого поля будет:
Из-за мягкого поля двойная форма SVM немного изменится на:
, где C называется штрафом.
Параметр C дает нам контроль над тем, как SVM будет обрабатывать ошибки.
Наблюдения:
- Большое значение C дает жесткий классификатор маржи.
- Небольшое значение C дает более широкую маржу за счет некоторой неправильной классификации.
- Ключ в том, чтобы найти правильное значение C.
9. Ядра:
Допустим, у нас есть данные, которые нельзя разделить линейно, и мы хотели бы использовать для них SVM. Данные распределяются в двумерном пространстве следующим образом:
Хотя наши данные находятся в двухмерном пространстве, которое не является линейно разделимым, и мы хотим применить к ним SVM.Одно из возможных решений для этого, например, преобразовать каждый двумерный вектор.
Теперь данные, преобразованные в Z-пространство, возможно, будут линейно разделимы.
Выбор используемого преобразования во многом зависит от вашего набора данных.
9.1 Что такое ядро?
В приведенном выше разделе мы видели, что данные, которые не являются линейно разделяемыми в более низких измерениях, становятся линейно разделяемыми в более высоких измерениях.
Один из его основных недостатков — нам необходимо преобразовать каждую точку данных (вектор) в более высокие измерения.
Если у нас есть миллионы векторов, и их преобразование сложно, может потребоваться огромное количество времени.
Это когда ядро пригодится, когда у нас есть такие проблемы.
На самом деле нам не нужен вектор, мы заботимся о скалярном произведении Xi и Xj между двумя примерами.
Короче говоря, функция ядра вычисляет скалярное произведение, как если бы они были преобразованы в Z-пространство, и делает это без выполнения преобразования и без вычисления скалярного произведения.
10. Уловка с ядром:
Теперь мы знаем, что такое ядро. Мы увидим, что такое трюк с ядром. Он определяется как,
Таким образом, мы можем записать двойную задачу с мягкими границами как,
Применение трюка ядра означает просто замену скалярного произведения двух векторов функцией ядра, и это то, что мы сделали в приведенной выше формулировке.
11. Типы ядра:
11.1 Линейное ядро:
Оно просто определяется как,
, где X` и X« — 2 вектора.
На практике линейное ядро хорошо работает для классификации текста.
11.2 Полиномиальное ядро:
Общая формула для полиномиального ядра определяется выражением,
, где p = постоянный член и q = степень ядраПо мере увеличения степени полиномиального ядра граница принятия решения будет становиться все более сложной. . Использование полиномиального ядра более высокой степени часто опасно, поскольку оно обеспечивает лучшую производительность на тестовых данных, но приводит к тому, что мы назвали переобучением.
11.3 Строковое ядро:
Строковое ядро - это строковая функция, которая работает с строковыми ядрами, которую можно интуитивно понять как функцию, измеряющую сходство пар строк, чем больше одинаковых двух строк a и b, тем выше значение строкового ядра K ( а, б) будет.
12. Ядро радиальной базисной функции (RBF) / Ядро Гаусса:
Иногда полиномиального ядра недостаточно для работы. По этой причине мы называем другое ядро, более сложное, ядром Гаусса.Ядро RBF — это функция, значение которой зависит от расстояния от начала координат или от некоторой точки.
Функция ядра RBF:
Регулируемый параметр sigma играет важную роль в производительности ядра и должен быть тщательно настроен на проблему как руку. Если оценка будет завышена, экспонента будет вести себя почти линейно, и многомерная проекция начнет терять свою нелинейную мощность. С другой стороны, при недооценке функция будет регуляризоваться, и граница решения будет очень чувствительна к шуму для обучающих данных.
13. Какое ядро когда использовать? :
Рекомендуемое ядро - ядро RBF, потому что оно хорошо работает. Ядро — это мера сходства между двумя векторами. Таким образом, знание предметной области проблемы может иметь наибольшее влияние на результаты. Также возможно создание собственного ядра.
Использование правильного ядра с правильным набором данных в одном из элементов нашего успеха или неудачи в SVM.
14. Интерпретация функции потерь SVM:
X + Y — 1 = 0
Zi + loss — 1 = 0
Если Zi больше или равно 1, то потеря = 0.
Если Zi меньше 1, то потеря = 1 — Zi.
Если точка классифицирована правильно, то Zi больше 1. Итак (1 — Zi) — некоторое отрицательное значение, а max (0, -ve значение) будет равно 0. Таким образом, потеря будет равна нулю.
Если точка классифицирована неправильно, то Zi меньше 1. Таким образом (1 — Zi) больше 0, а max (0, больше 0) будет вторым членом. Таким образом, потеря больше 0.
15. SVM как регрессор (SVR):
Проблема регрессии — это обобщение проблемы классификации в SVM, в которой модель будет возвращать непрерывные значения вместо дискретных значений.
Ограничения в задаче регрессии состоят в том, чтобы минимизировать ошибку между прогнозируемым выходом и фактическим выходом. SVR использует ε-нечувствительную функцию потерь. Значение ε определяет ширину поля. Меньшие значения указывают на более низкий допуск на ошибку. Интуитивно понятно, что при уменьшении ε запас сдвигается внутрь. Итак, наша задача оптимизации изменится на,
Здесь ε — гиперпараметр.
Если ε меньше, мы допускаем очень небольшие ошибки в обучающих данных, которые вызывают переобучение.
Если ε велико, мы допускаем больше ошибок в обучающих данных, что приводит к недостаточной подгонке.
Как мы видели в SVC, есть все версии ядра SVR, которые позволят нам подогнать нелинейные данные.
16. Гиперпараметры и компромисс смещения и дисперсии:
Гиперпараметры SVC — это γ (ядро RBF) и C (мягкий край).
Если C очень велико, это SVM с жестким запасом. Так что это высокая дисперсия (переобучение).
Если C очень мало, значит, это большое смещение (недостаточное соответствие).
Если γ мало, то модель не подходит.
Если значение γ велико, то модель переобучается.
17. Временная и пространственная сложность для SVM:
Допустим, у нас есть набор данных, который имеет n точек данных и m функций, тогда
во время поездаT (n) = O (mk) во время тестирования
Где k = опорные векторы
S (n) = O (k)
Потому что нам нужно хранить k векторов.
18. Плюсы и минусы SVM:
Плюсы:
- Хорошо работает в более высоких измерениях.
- Эффективен, когда количество примеров меньше количества измерений.
- Это эффективно с точки зрения памяти, поскольку в функции принятия решения используется подмножество обучающих точек (называемых опорными векторами).
Минусы:
- Он не работает, когда данные очень большие, потому что время, необходимое для обучения, полиномиально.
- Он также не работает, когда данные содержат больше шума.
- Модель ядра не интерпретируется.
Ссылки:
- Машинное обучение от Caltech
2. Введение в машинное обучение Алпайдина Этхема
Руководство:
И. Харшалл, доцент инженерного колледжа Ламбай , Новый Панвел.
“ Я хотел бы выразить свою благодарность Харшаллу Сэру за руководство и техническую поддержку. Ваши отличные педагогические навыки и вежливый характер очень помогли мне в моем путешествии по этой статье. ”
II. Дхирадж Амин, доцент инженерного колледжа Пиллай, Нью-Панвел.
Математика в основе SVM | Math Behind Support Vector Machine
Эта статья была опубликована в рамках Блогатона Data Science.
Введение
Один из классификаторов, с которыми мы сталкиваемся при изучении машинного обучения, — это Support Vector Machine или SVM. Этот алгоритм является одним из самых популярных алгоритмов классификации, используемых в машинном обучении.
В этой статье мы узнаем о математике, лежащей в основе машины опорных векторов для задачи классификации, о том, как она классифицирует классы и дает прогнозы.
Содержание
- Мягкое знакомство с машиной опорных векторов (SVM)
- Несколько концепций, которые нужно знать, прежде чем узнавать секрет алгоритма
- Погружение в море математики
- 3.1 Где использовать SVM / Предыстория SVM
- 3.1.1 Случай 1: Идеально разделенный двоичный классифицированный набор данных
- 3.1.2 Уравнение идеального разделения
- 3.2 Случай 2: Набор данных несовершенного разделения
- 3.2.1 Окончательное уравнение для решения несовершенного разделения
- 3.2.2 Первичный — Двойной — Лагранжиан
- 3.2.3 Использование ядра для получения окончательных результатов
- 3.1 Где использовать SVM / Предыстория SVM
- Конечные точки
1. Машина опорных векторов
Машина опорных векторов или SVM — это алгоритм машинного обучения, который просматривает данные и сортирует их по одной из двух категорий.
Машина опорных векторов — это контролируемый линейный алгоритм машинного обучения, наиболее часто используемый для решения задач классификации и также называемый классификацией опорных векторов.
Существует также подмножество SVM, называемое SVR, что означает регрессию опорных векторов, которая использует те же принципы для решения задач регрессии.
SVM наиболее часто используется и эффективен из-за использования метода ядра, который в основном помогает очень легко решить нелинейность уравнения.
П.С. — Поскольку данная статья написана с упором на математическую часть. Пожалуйста, обратитесь к этой статье для получения полного обзора работы алгоритма
.2. Основные темы для SVM
Support Vector Machine в основном помогает в сортировке данных по двум или более категориям с помощью границы для различения похожих категорий.
Итак, сначала давайте пересмотрим формулы того, как данные представлены в пространстве, и что такое уравнение линии, которое поможет в разделении схожих категорий, и, наконец, формула расстояния между точкой данных и линией (граница, разделяющая категории).
2,1 Точка в пространстве
Предположим, у нас есть некоторые данные, в которых нас (алгоритм SVM) просят различать мужчин и женщин на основе сначала изучения характеристик обоих полов, а затем точно пометить невидимые данные, если кто-то — мужчина или женщина.
В этом примере характеристики, которые помогут различать пол, в основном называются функциями в машинном обучении.
Домен, Ко-домен, Диапазон
Предполагается, что мы уже знакомы с концепцией области, диапазона и совместной области при определении функции в реальном пространстве.(Если нет, пожалуйста, нажмите на изображение, чтобы понять концепцию на примере)
Когда мы определяем x в реальном пространстве, мы понимаем его домен, а при отображении функции для y = f (x) мы получаем диапазон и ко-домен.
Итак, изначально нам даны данные, которые должен быть разделен алгоритмом.
Данные для разделения / классификации представлены как уникальная точка в пространстве, где каждая точка представлена некоторым вектором признаков x.D это векторное пространство с размерностью D, для этого алгоритма не обязательно владеть этой концепцией.
Мы применяем аналогичную концепцию области, диапазона, отображения функции для точек данных здесь, вместо реального пространства, у нас есть векторное пространство для x.
Далее, отображая точку в комплексном пространстве признаков x,
Φ (x) ∊ R M
Преобразованное пространство признаков для каждого входного признака, сопоставленного преобразованному базисному вектору Φ (x), может быть определено как:
2.2 Граница решенияИтак, теперь, когда мы представили наши точки визуально, наша следующая задача — разделить эти точки с помощью линии, и именно здесь термин «граница принятия решения» появляется на картинке.
Граница принятия решения — это главный разделитель для разделения точек на соответствующие классы.
(Как и почему я говорю, что основной разделитель, а не просто любой разделитель, мы рассмотрим, понимая математику)
Уравнение гиперплоскости:Уравнение главной разделительной линии называется уравнением гиперплоскости.
Давайте посмотрим на уравнение для прямой с наклоном m и точкой пересечения c.
Уравнение принимает следующий вид: mx + c = 0
(Обратите внимание: мы поместили прямую / линейную линию, которая представляет собой 1-D в 2-мерном пространстве)
Уравнение гиперплоскости, разделяющее точки (для классификации), теперь может быть легко записано как:
H: w T (x) + b = 0
Здесь: b = член перехвата и смещения уравнения гиперплоскости
В D-мерном пространстве гиперплоскость всегда будет оператором D -1.
Например, для двумерного пространства гиперплоскость — это прямая линия (1-D).
2.3 Измерение расстояния
Теперь, когда мы увидели, как представлять точки данных и как провести разделительную линию между точками. Но при установке разделительной линии нам, очевидно, нужна такая линия, которая могла бы разделить точки данных наилучшим образом с наименьшим количеством ошибок / ошибок неправильной классификации.
Итак, чтобы иметь наименьшее количество ошибок в классификации точек данных, эта концепция потребует, чтобы мы сначала знали расстояние между точкой данных и разделяющей линией.
Расстояние до любой прямой ax + by + c = 0 от заданной точки, скажем, (x 0 , y 0 ), определяется как d.
Аналогично, расстояние в уравнении гиперплоскости: w T Φ (x) + b = 0 от заданного точечного вектора Φ (x 0 ) может быть легко записано как:
здесь || w || 2 — евклидова норма для длины w, определяемая по формуле:
Теперь, когда термины понятны, давайте углубимся в алгоритм, который используется в основе.
3. В море много
3.1 Справочная информация
Мы говорили о примере различения полов, поэтому такие задачи называются проблемами классификации. Теперь задача классификации может иметь только два (бинарных) класса для разделения или может иметь более двух классов, которые известны как задачи классификации нескольких классов.
Но не все модели прогнозирования классификации поддерживают мультиклассовую классификацию, такие алгоритмы, как логистическая регрессия и машины опорных векторов (SVM), были разработаны для двоичной классификации и изначально не поддерживают задачи классификации с более чем двумя классами.
Но если кто-то по-прежнему хочет использовать алгоритмы двоичной классификации для задач множественной классификации, один из широко используемых подходов состоит в том, чтобы разделить наборы данных многоклассовой классификации на несколько наборов данных двоичной классификации, а затем подобрать для каждого из них модель двоичной классификации.
Двумя разными примерами этого подхода являются стратегии «Один против остальных» и «Один против одного». О двух подходах можно прочитать здесь.
Продвигаясь вперед к основной теме понимания математики, мы будем рассматривать проблему классификации двоичных классов по двум причинам:
- Как уже было сказано выше, SVM намного лучше работает для двоичного класса
- Было бы легко понять математику, поскольку наша целевая переменная (переменные / невидимые данные, предназначенные для прогнозирования, является ли точка мужчиной или женщиной)
- Примечание. Это будет подход «один против одного».
3.1.1 Случай 1: (Идеальное разделение двоичных секретных данных) —
Продолжая наш пример, если гиперплоскость сможет идеально различать мужчин и женщин без каких-либо ошибок классификации, то такой случай разделения известен как Идеальное разделение.
Здесь, на рисунке, если мужчины зеленые, а женщины красные, и мы можем видеть, что гиперплоскость, которая здесь является линией, полностью различает эти два класса.
В общем, данные имеют две классификации , положительную и отрицательную группы , и их можно полностью разделить, что означает, что гиперплоскость может точно разделить * обучающие классы *.
**
( Данные обучения — Данные, с помощью которых алгоритм / модель изучает шаблон того, как различать, глядя на функции
Данные тестирования — После обучения модели на данных обучения модели предлагается предсказать значения для невидимых данные, где указаны только характеристики, и теперь модель скажет, мужчина это или женщина)
**
Теперь может быть много гиперплоскостей, дающих 100% точности, , как видно на фотографии.
«» Итак, чтобы выбрать оптимальную / лучшую гиперплоскость, поместите гиперплоскость прямо в центр, где расстояние является максимальным от ближайших точек, и укажите наименьшие ошибки тестирования в дальнейшем. «»
Обратите внимание: мы должны стремиться к минимуму ТЕСТОВЫХ ошибок, а НЕ ОБУЧАЮЩИХ ошибок.
Итак, мы должны максимизировать расстояние, чтобы дать некоторое пространство для уравнения гиперплоскости, что также является целью / основной идеей SVM.
Цель алгоритма, задействованного в SVM:Итак, теперь у нас есть:
При поиске гиперплоскости с максимальным запасом (поле в основном представляет собой защищенное пространство вокруг уравнения гиперплоскости) и алгоритм пытается получить максимальный запас с ближайшими точками (известными как опорные векторы).
Другими словами, “ Цель состоит в том, чтобы максимизировать минимальное расстояние. ” для расстояния (упомянутого ранее в разделе 2)
, выдано:
Итак, теперь цель понятна. Делая прогнозы на обучающих данных, которые были двоично классифицированы как положительные и отрицательные группы, если точка заменяется из положительной группы в уравнении гиперплоскости, мы получим значение больше 0 (ноль), математически
w T ( Φ (x)) + b> 0
И предсказания из отрицательной группы в уравнении гиперплоскости дадут отрицательное значение как
.w T ( Φ (x)) + b <0.
Но здесь признаки касались данных обучения, которым мы обучаем нашу модель. Что касается положительного класса, дайте положительный знак, а для отрицательного — отрицательный.
Но при тестировании этой модели на тестовых данных, если мы правильно предсказываем положительный класс (положительный знак или знак больше нуля) как положительный, то два положительных результата дают положительный результат и, следовательно, результат больше нуля. То же самое применимо, если мы правильно предсказываем отрицательную группу, поскольку два отрицательных результата снова дадут положительную.
Но если промах модели классифицирует положительную группу как отрицательную, то один плюс и один минус составляют минус, следовательно, в целом меньше нуля.
Резюмируя вышеупомянутую концепцию:
Произведение предсказанной и фактической метки будет больше 0 (нуля) при правильном предсказании, в противном случае меньше нуля.
Для идеально разделяемых наборов данных оптимальная гиперплоскость правильно классифицирует все точки, дополнительно подставляя оптимальные значения в уравнение веса.
Здесь :
arg max — это сокращение для аргументов максимумов, которые в основном являются точками области определения функции, в которых значения функции максимальны.
(Подробнее о работе с arg max в машинном обучении читайте здесь.)
Далее, вынесение независимого члена массы наружу дает:
Внутренний член (min n y n | w T Φ (x) + b |) в основном представляет собой минимальное расстояние от точки до границы принятия решения и ближайшую точку к границе принятия решения H.
Масштабирование расстояния до ближайшей точки на 1, т.е. (min n y n | w T Φ (x) + b |) = 1. Здесь векторы остаются в том же направлении и уравнение гиперплоскости не изменится. Это похоже на изменение масштаба изображения; объекты расширяются или сжимаются, но направления остаются неизменными, а изображение остается неизменным.
Масштабирование расстояния выполняется заменой,
Уравнение теперь принимает вид (описывающий, что каждая точка находится на расстоянии не менее 1 / || w || 2 от гиперплоскости) как
Эта задача максимизации эквивалентна следующей задаче минимизации, которая умножается на константу, поскольку они не влияют на результаты.
3.1.2 Первичная форма SVM (идеальное разделение):Вышеупомянутая оптимизационная задача является первичной формулировкой, поскольку в постановке задачи используются исходные переменные.
3,2 ВАРИАНТ 2: (Неидеальное разделение)Но все мы знаем, что не бывает ситуации, когда все идеально и всегда что-то идет наоборот.
В нашем примере гендерной классификации мы не можем ожидать, что модель даст такое уравнение гиперплоскости, которое будет идеально разделять оба пола, всегда будет одна или несколько точек, которые не попадут в их категорию, в то время как оптимальная гиперплоскость уравнение соответствует, известное как классификация ошибок.(Как показано на изображении ниже)
Итак, мы не можем ожидать идеального / идеального корпуса. Здесь мы становимся умнее модели и позволяем модели сделать несколько ошибок при классификации точек и, следовательно,
И, следовательно, добавьте переменную резерва в качестве штрафа за каждую ошибку классификации для каждой точки данных, представленной β (бета). Таким образом, отсутствие штрафа означает, что точка данных правильно классифицирована, β = 0, и при любом пропуске классификации β> 1 как штраф.
3.2.1 Первичная форма SVM (несовершенное разделение):Здесь: для β и C
Промежуток времени для каждой переменной должен быть как можно меньше и дополнительно регуляризован гиперпараметром C
Если C = 0, означает менее сложную границу, поскольку классификатор не будет наказан провисанием, в результате оптимальная гиперплоскость может использовать его где угодно и принять все большие ошибки классификации. И в результате граница принятия решения будет линейной и недостаточно подогнанной.
Приведенное выше уравнение является примером Convex Quadratic Optimization , поскольку целевая функция квадратична по W, а ограничения линейны по W и β.
Решение для первичной формы : (Неидеальное разделение):
Так как у нас есть Φ, который имеет сложные обозначения. мы бы переписали уравнение.
Концепцияв основном состоит в том, чтобы избавиться от Φ и, следовательно, переписать первичную формулировку в двойной формулировке, известной как двойная форма задачи, и решить полученную задачу оптимизации ограничений с помощью метода множителя Лагранжа.
Другими словами:
Двойная форма: переписывает ту же задачу с использованием другого набора переменных. Таким образом, альтернативная формулировка поможет устранить зависимость от Φ, а уменьшение эффекта будет сделано с помощью кернелизации.
Метод множителя Лагранжа: Это стратегия нахождения локальных минимумов или максимумов функции при условии, что одно или несколько уравнений должны точно удовлетворяться выбранными значениями переменных.
Далее, формальное определение двойной задачи может быть определено как:
Лагранжева двойственная задача получается путем сначала формирования лагранжиана уже полученной задачи минимизации с помощью множителя Лагранжа, так что новые ограничения могут быть добавлены к целевой функции , а затем будут решены для значений основных переменных. , которые минимизируют исходную целевую функцию
Это новое решение делает простые переменные функциями множителей Лагранжа и называются двойными переменными, поэтому новая задача состоит в том, чтобы максимизировать целевую функцию для двойственных переменных с новыми производными ограничениями.
Этот блог очень хорошо объяснил работу множителей Лагранжа.
Рассмотрим пример применения множителя Лагранжа для лучшего понимания того, как преобразовать первичную формулировку с использованием множителей Лагранжа для решения для оптимизации .
Ниже x — исходная первичная переменная и минимизация функции f при наборе ограничений, заданных g, и переписывание для нового набора переменных, называемых лагранжевыми множителями.
Решение основных переменных путем дифференцирования неограниченного Лагранжа.
И, наконец, подставляем обратно в уравнение Лагранжа и переписываем ограничения
Возвращаясь к нашей изначальной форме:
Шаг 1: Получить первичную и определить лагранжевую форму из первичной
Шаг 2: Получение решения путем выражения первичного числа в форме двойников
Шаг 3: Подставить полученные значения в лагранжевую форму
Окончательная двойная форма из приведенного выше упрощения:
Вышеупомянутая двойная форма все еще имеет члены Φ, и здесь это может быть легко решено с помощью Kernelization
Ядро по определению избегает явного отображения, которое необходимо для получения алгоритмов линейного обучения для изучения нелинейной функции или границы решения Для всех x и x ‘во входном пространстве Φ некоторые функции k (x, x’) могут быть выражены как внутренний продукт в другом пространстве Ψ.Функция
упоминается как Ядро . Короче говоря, для машинного обучения ядро определяется как написанное в форме «карты функций»
, что удовлетворяет
Для лучшего понимания ядер можно обратиться к по этой ссылке на Quora
.Ядро имеет два свойства:
Симметричный по своей природе k (x n , x m ) = k (x m , x n )
Положительно полуопределенный
Чтобы иметь представление о работе ядер, может быть полезна эта ссылка кворума.
По определению ядра мы можем подставить эти значения
Таким образом, подставляя свойства ядра и по определению ядра в нашу двойную форму,
Мы получаем Новое уравнение как:
4. Обозначение всех шагов, упомянутых выше.И это решение не содержит Φ и его гораздо проще вычислить. -й — математика, лежащая в основе модели SVM.
Наконец, мы подошли к концу статьи, и подведем итоги всей тарабарщины, написанной выше
.- Всякий раз, когда нам дается любой тестовый вектор признаков x для прогнозирования, который отображается в комплекс Φ (x) и просят предсказать, который в основном равен w T Φ (x)
- Затем перепишите его, используя двойники, чтобы прогноз был полностью независим от базиса комплексных признаков Φ
- И дополнительно прогнозируется с использованием ядер
- Отсюда можно сделать вывод, что нам не нужна сложная основа для хорошего моделирования неразрывных данных, и ядро выполняет эту работу.
Надеюсь, мне удалось раскрыть основы интуиции и математики, лежащие в основе SVM, Для модели классификатора и учитывая длину статьи, я попытался прикрепить все важные ссылки к соответствующим ссылкам в статье. Это было мое понимание задействованной математики в SVM, и я открыт для предложений относительно моей работы здесь
% PDF-1.6
%
1609 0 объект
>
эндобдж
xref
1609 815
0000000016 00000 н.
0000019515 00000 п.
0000020555 00000 п.
0000020688 00000 п.
0000020726 00000 п.
0000030980 00000 п.
0000031210 00000 п.
0000031359 00000 п.
0000031546 00000 п.
0000031695 00000 п.
0000031883 00000 п.
0000032794 00000 п.
0000033004 00000 п.
0000033043 00000 п.
0000033133 00000 п.
0000044607 00000 п.
0000052423 00000 п.
0000057616 00000 п.
0000062715 00000 н.
0000067276 00000 п.
0000072185 00000 п.
0000072388 00000 п.
0000072945 00000 п.
0000073126 00000 п.
0000075476 00000 п.
0000075941 00000 п.
0000076156 00000 п.
0000077306 00000 п.
0000078286 00000 п.
0000079474 00000 п.
0000080059 00000 п.
0000081243 00000 п.
0000085475 00000 п.
0000093544 00000 п.
0000096237 00000 п.
0000104587 00000 н.
0000110521 00000 п.
0000111822 00000 н.
0000111883 00000 н.
0000111930 00000 н.
0000111982 00000 н.
0000112288 00000 н.
0000112476 00000 н.
0000112899 00000 н.
0000113087 00000 н.
0000113620 00000 н.
0000113742 00000 н.
0000127831 00000 н.
0000127872 00000 н.
0000128407 00000 н.
0000128525 00000 н.
0000152199 00000 н.
0000152240 00000 н.
0000152738 00000 н.
0000152837 00000 н.
0000153515 00000 н.
0000153669 00000 н.
0000154272 00000 н.
0000154427 00000 н.
0000154582 00000 н.
0000155193 00000 н.
0000155348 00000 н.
0000155946 00000 н.
0000156101 00000 п.
0000156256 00000 н.
0000156410 00000 н.
0000156565 00000 н.
0000156720 00000 н.
0000156874 00000 н.
0000157029 00000 н.
0000157183 00000 н.
0000157338 00000 н.
0000157493 00000 н.
0000157646 00000 н.
0000157801 00000 н.
0000157955 00000 н.
0000158110 00000 н.
0000158263 00000 н.
0000158417 00000 н.
0000158571 00000 н.
0000158725 00000 н.
0000158878 00000 н.
0000159033 00000 н.
0000159188 00000 н.
0000159342 00000 н.
0000159497 00000 н.
0000159651 00000 н.
0000159805 00000 н.
0000159959 00000 н.
0000160113 00000 п.
0000160267 00000 н.
0000160421 00000 н.
0000160575 00000 н.
0000160730 00000 н.
0000160885 00000 н.
0000161039 00000 н.
0000161194 00000 н.
0000161348 00000 н.
0000161503 00000 н.
0000161657 00000 н.
0000161811 00000 н.
0000161965 00000 н.
0000162119 00000 н.
0000162273 00000 н.
0000162428 00000 н.
0000162583 00000 н.
0000162736 00000 н.
0000162891 00000 н.
0000163046 00000 н.
0000163202 00000 н.
0000163358 00000 н.
0000163514 00000 н.
0000163670 00000 н.
0000163828 00000 н.
0000163984 00000 н.
0000164139 00000 н.
0000164736 00000 н.
0000164893 00000 н.
0000165470 00000 н.
0000165626 00000 н.
0000166212 00000 н.
0000166368 00000 н.
0000166934 00000 н.
0000167091 00000 н.
0000167249 00000 н.
0000167405 00000 н.
0000167560 00000 н.
0000167715 00000 н.
0000167872 00000 н.
0000168027 00000 н.
0000168182 00000 н.
0000168337 00000 н.
0000168494 00000 н.
0000168651 00000 п.
0000168808 00000 н.
0000168965 00000 н.
0000169120 00000 н.
0000169276 00000 н.
0000169433 00000 н.
0000169590 00000 н.
0000169747 00000 н.
0000169902 00000 н.
0000170059 00000 н.
0000170216 00000 н.
0000170371 00000 н.
0000170528 00000 н.
0000170684 00000 н.
0000170840 00000 н.
0000170997 00000 н.
0000171154 00000 н.
0000171310 00000 н.
0000171467 00000 н.
0000171622 00000 н.
0000171779 00000 н.
0000171936 00000 н.
0000172091 00000 н.
0000172248 00000 н.
0000172405 00000 н.
0000172562 00000 н.
0000172719 00000 н.
0000172876 00000 н.
0000173033 00000 н.
0000173190 00000 н.
0000173345 00000 н.
0000173502 00000 н.
0000173659 00000 н.
0000173816 00000 н.
0000173973 00000 н.
0000174130 00000 н.
0000174287 00000 н.
0000174443 00000 н.
0000174599 00000 н.
0000174756 00000 н.
0000174912 00000 н.
0000175199 00000 н.
0000175350 00000 н.
0000175505 00000 н.
0000175662 00000 н.
0000175819 00000 н.
0000175976 00000 н.
0000176133 00000 н.
0000176289 00000 н.
0000176446 00000 н.
0000176603 00000 н.
0000176760 00000 н.
0000176917 00000 н.
0000177074 00000 н.
0000177229 00000 н.
0000177385 00000 н.
0000177541 00000 н.
0000177696 00000 н.
0000177853 00000 н.
0000178010 00000 н.
0000178167 00000 н.
0000178323 00000 н.
0000178480 00000 н.
0000178637 00000 н.
0000178793 00000 н.
0000178947 00000 н.
0000179103 00000 н.
0000179259 00000 н.
0000179416 00000 н.
0000179573 00000 н.
0000179729 00000 н.
0000179886 00000 н.
0000180043 00000 н.
0000180198 00000 п.
0000180354 00000 н.
0000180510 00000 н.
0000180665 00000 н.
0000180821 00000 н.
0000180978 00000 н.
0000181135 00000 н.
0000181719 00000 н.
0000181873 00000 н.
0000182442 00000 н.
0000182596 00000 н.
0000183166 00000 н.
0000183321 00000 н.
0000183476 00000 н.
0000184038 00000 н.
0000184193 00000 н.
0000184347 00000 н.
0000184501 00000 н.
0000184656 00000 н.
0000184811 00000 н.
0000184966 00000 н.
0000185121 00000 н.
0000185273 00000 н.
0000185426 00000 н.
0000185579 00000 п.
0000185734 00000 н.
0000185887 00000 н.
0000186042 00000 н.
0000186197 00000 н.
0000186352 00000 н.
0000186506 00000 н.
0000186661 00000 н.
0000186816 00000 н.
0000186970 00000 н.
0000187124 00000 н.
0000187279 00000 н.
0000187432 00000 н.
0000187586 00000 п.
0000187741 00000 н.
0000187896 00000 н.
0000188051 00000 н.
0000188206 00000 н.
0000188361 00000 н.
0000188516 00000 н.
0000188670 00000 н.
0000188824 00000 н.
0000188978 00000 н.
0000189132 00000 н.
0000189286 00000 н.
0000189441 00000 н.
0000189592 00000 н.
0000189747 00000 н.
0000189901 00000 н.
00001 00000 н.
00001
00000 н. 00001 00000 н. 00001 00000 н. 00001
00000 н. 00001
00000 н. 00001 00000 н. 00001 00000 н. 0000100000 н. 00001
00000 н. 00001
00000 н. 00001 00000 н.
00001 00000 н.
0000192531 00000 н.
0000192685 00000 н.
0000192839 00000 н.
0000192993 00000 н.
0000193148 00000 н.
0000193301 00000 н.
0000193455 00000 н.
0000193609 00000 н.
0000193762 00000 н.
0000193915 00000 н.
0000194070 00000 н.
0000194225 00000 н.
0000194379 00000 н.
0000194533 00000 н.
0000194686 00000 н.
0000195305 00000 н.
0000195460 00000 н.
0000195615 00000 н.
0000195769 00000 н.
0000195924 00000 н.
0000196078 00000 н.
0000196233 00000 н.
0000196387 00000 н.
0000196542 00000 н.
0000196697 00000 н.
0000196851 00000 н.
0000197005 00000 н.
0000197159 00000 н.
0000197314 00000 н.
0000197469 00000 н.
0000197623 00000 н.
0000197777 00000 н.
0000197931 00000 н.
0000198087 00000 н.
0000198632 00000 н.
0000198789 00000 н.
0000199323 00000 н.
0000199480 00000 н.
0000200022 00000 н.
0000200178 00000 н.
0000200706 00000 н.
0000200862 00000 н.
0000201019 00000 н.
0000201174 00000 н.
0000201709 00000 н.
0000201866 00000 н.
0000202383 00000 н.
0000202540 00000 н.
0000203058 00000 н.
0000203215 00000 н.
0000203735 00000 н.
0000203892 00000 н.
0000204049 00000 н.
0000204204 00000 н.
0000204361 00000 н.
0000204518 00000 н.
0000204675 00000 н.
0000204832 00000 н.
0000204987 00000 н.
0000205143 00000 н.
0000205299 00000 н.
0000205456 00000 н.
0000205613 00000 н.
0000205770 00000 н.
0000205926 00000 н.
0000206083 00000 н.
0000206239 00000 н.
0000206396 00000 н.
0000206553 00000 н.
0000206707 00000 н.
0000206861 00000 н.
0000207018 00000 н.
0000207175 00000 н.
0000207332 00000 н.
0000207489 00000 н.
0000207646 00000 н.
0000207803 00000 н.
0000207959 00000 н.
0000208116 00000 н.
0000208273 00000 н.
0000208428 00000 н.
0000208584 00000 н.
0000208740 00000 н.
0000208897 00000 н.
0000209054 00000 н.
0000209210 00000 н.
0000209366 00000 н.
0000209523 00000 н.
0000209678 00000 н.
0000209835 00000 н.
0000209992 00000 н.
0000210147 00000 н.
0000210304 00000 п.
0000210461 00000 п.
0000210617 00000 н.
0000210774 00000 п.
0000210931 00000 н.
0000211087 00000 н.
0000211244 00000 н.
0000211401 00000 п.
0000211557 00000 н.
0000211713 00000 н.
0000211869 00000 н.
0000212025 00000 н.
0000212182 00000 н.
0000212339 00000 н.
0000212495 00000 н.
0000212652 00000 н.
0000212809 00000 н.
0000212966 00000 н.
0000213123 00000 н.
0000213280 00000 н.
0000213437 00000 н.
0000213591 00000 н.
0000213748 00000 н.
0000213905 00000 н.
0000214062 00000 н.
0000214218 00000 н.
0000214375 00000 н.
0000214531 00000 н.
0000214687 00000 н.
0000214844 00000 н.
0000215001 00000 н.
0000215158 00000 н.
0000215313 00000 н.
0000215470 00000 н.
0000215627 00000 н.
0000215784 00000 н.
0000215941 00000 н.
0000216098 00000 н.
0000216255 00000 н.
0000216412 00000 н.
0000216569 00000 н.
0000216726 00000 н.
0000216883 00000 н.
0000217038 00000 п.
0000217192 00000 н.
0000217349 00000 н.
0000217506 00000 н.
0000217662 00000 н.
0000217818 00000 н.
0000217975 00000 н.
0000218130 00000 н.
0000218287 00000 н.
0000218444 00000 н.
0000218600 00000 н.
0000218755 00000 н.
0000218911 00000 п.
0000219068 00000 н.
0000219225 00000 н.
0000219381 00000 п.
0000219538 00000 п.
0000219693 00000 п.
0000219849 00000 н.
0000220006 00000 н.
0000220162 00000 н.
0000220318 00000 н.
0000220475 00000 н.
0000220631 00000 н.
0000220788 00000 н.
0000220945 00000 н.
0000221102 00000 п.
0000221259 00000 н.
0000221415 00000 н.
0000221571 00000 н.
0000221728 00000 н.
0000221885 00000 н.
0000222042 00000 н.
0000222199 00000 н.
0000222355 00000 н.
0000222512 00000 н.
0000222669 00000 н.
0000222826 00000 н.
0000222983 00000 н.
0000223138 00000 н.
0000223294 00000 н.
0000223450 00000 н.
0000223607 00000 н.
0000223762 00000 н.
0000223919 00000 н.
0000224075 00000 н.
0000224232 00000 н.
0000224388 00000 н.
0000224543 00000 н.
0000224700 00000 н.
0000224857 00000 н.
0000225014 00000 н.
0000225171 00000 н.
0000225328 00000 н.
0000225484 00000 н.
0000225641 00000 н.
0000225797 00000 н.
0000225954 00000 н.
0000226110 00000 н.
0000226263 00000 н.
0000226420 00000 н.
0000226577 00000 н.
0000226733 00000 н.
0000226889 00000 н.
0000227046 00000 н.
0000227203 00000 н.
0000227359 00000 н.
0000227515 00000 н.
0000227672 00000 н.
0000227828 00000 н.
0000227985 00000 н.
0000228141 00000 п.
0000228297 00000 н.
0000228454 00000 н.
0000228611 00000 н.
0000228768 00000 н.
0000228924 00000 н.
0000229081 00000 н.
0000229237 00000 н.
0000229393 00000 п.
0000229549 00000 н.
0000229705 00000 н.
0000229862 00000 н.
0000230017 00000 н.
0000230172 00000 н.
0000230327 00000 н.
0000230482 00000 н.
0000230637 00000 п.
0000231166 00000 н.
0000231321 00000 н.
0000231476 00000 н.
0000231996 00000 н.
0000232151 00000 н.
0000232676 00000 н.
0000232831 00000 н.
0000233348 00000 п.
0000233503 00000 н.
0000233658 00000 п.
0000233812 00000 н.
0000233967 00000 н.
0000234122 00000 н.
0000234277 00000 н.
0000234432 00000 н.
0000234586 00000 н.
0000234741 00000 н.
0000234896 00000 н.
0000235051 00000 н.
0000235206 00000 н.
0000235361 00000 п.
0000235515 00000 н.
0000235670 00000 н.
0000235825 00000 н.
0000235980 00000 н.
0000236135 00000 н.
0000236289 00000 н.
0000236444 00000 н.
0000236599 00000 н.
0000236754 00000 н.
0000236909 00000 н.
0000237064 00000 н.
0000237219 00000 н.
0000237374 00000 н.
0000237529 00000 н.
0000237684 00000 н.
0000237837 00000 н.
0000237990 00000 н.
0000238145 00000 н.
0000238300 00000 н.
0000238455 00000 н.
0000238610 00000 н.
0000238765 00000 н.
0000238916 00000 н.
0000239071 00000 н.
0000239226 00000 н.
0000239380 00000 н.
0000239535 00000 п.
0000239690 00000 н.
0000239844 00000 н.
0000239999 00000 н.
0000240154 00000 н.
0000240307 00000 н.
0000240461 00000 п.
0000240616 00000 н.
0000240770 00000 н.
0000240924 00000 н.
0000241079 00000 п.
0000241233 00000 н.
0000241387 00000 н.
0000241540 00000 н.
0000241695 00000 н.
0000241849 00000 н.
0000242004 00000 н.
0000242158 00000 н.
0000242312 00000 н.
0000242467 00000 н.
0000242622 00000 н.
0000242777 00000 н.
0000242932 00000 н.
0000243087 00000 н.
0000243242 00000 н.
0000243397 00000 н.
0000243552 00000 н.
0000243707 00000 н.
0000243862 00000 н.
0000244017 00000 н.
0000244172 00000 н.
0000244327 00000 н.
0000244482 00000 н.
0000244637 00000 н.
0000244792 00000 н.
0000244947 00000 н.
0000245101 00000 п.
0000245256 00000 н.
0000245411 00000 н.
0000245566 00000 н.
0000245721 00000 н.
0000245876 00000 н.
0000246030 00000 н.
0000246185 00000 н.
0000246340 00000 н.
0000246495 00000 н.
0000246648 00000 н.
0000246803 00000 н.
0000246957 00000 н.
0000247111 00000 н.
0000247265 00000 н.
0000247418 00000 н.
0000247573 00000 н.
0000247728 00000 н.
0000247883 00000 н.
0000248037 00000 н.
0000248190 00000 н.
0000248345 00000 н.
0000248500 00000 н.
0000248655 00000 н.
0000248810 00000 н.
0000248965 00000 н.
0000249120 00000 н.
0000249275 00000 н.
0000249430 00000 н.
0000249585 00000 н.
0000249739 00000 н.
0000249893 00000 н.
0000250048 00000 н.
0000250203 00000 н.
0000250358 00000 н.
0000250513 00000 н.
0000250668 00000 н.
0000250822 00000 н.
0000250977 00000 н.
0000251132 00000 н.
0000251287 00000 н.
0000251441 00000 н.
0000251595 00000 н.
0000251750 00000 н.
0000251905 00000 н.
0000252060 00000 н.
0000252215 00000 н.
0000252370 00000 н.
0000252523 00000 н.
0000252678 00000 н.
0000252833 00000 н.
0000252988 00000 н.
0000253141 00000 п.
0000253296 00000 н.
0000253451 00000 н.
0000253606 00000 н.
0000253761 00000 н.
0000253916 00000 н.
0000254070 00000 н.
0000254225 00000 н.
0000254380 00000 н.
0000254534 00000 н.
0000254689 00000 н.
0000254843 00000 н.
0000254996 00000 н.
0000255151 00000 п.
0000255305 00000 н.
0000255460 00000 н.
0000255613 00000 н.
0000255766 00000 н.
0000255921 00000 н.
0000256076 00000 н.
0000256229 00000 н.
0000256383 00000 п.
0000256537 00000 н.
0000256692 00000 н.
0000256845 00000 н.
0000257000 00000 н.
0000257155 00000 н.
0000257310 00000 н.
0000257465 00000 н.
0000257620 00000 н.
0000257775 00000 н.
0000257930 00000 н.
0000258085 00000 н.
0000258240 00000 н.
0000258395 00000 н.
0000258550 00000 н.
0000258705 00000 н.
0000258860 00000 н.
0000259014 00000 н.
0000259168 00000 н.
0000259323 00000 н.
0000259478 00000 н.
0000259633 00000 н.
0000259788 00000 н.
0000259943 00000 н.
0000260098 00000 н.
0000260253 00000 н.
0000260408 00000 п.
0000260563 00000 н.
0000260718 00000 н.
0000260873 00000 н.
0000261028 00000 н.
0000261183 00000 н.
0000261337 00000 н.
0000261491 00000 н.
0000261646 00000 н.
0000261801 00000 н.
0000261956 00000 н.
0000262111 00000 п.
0000262266 00000 н.
0000262421 00000 н.
0000262576 00000 н.
0000262730 00000 н.
0000262885 00000 н.
0000263040 00000 н.
0000263195 00000 н.
0000263349 00000 п.
0000263504 00000 н.
0000263659 00000 н.
0000263814 00000 н.
0000263968 00000 н.
0000264122 00000 н.
0000264276 00000 н.
0000264430 00000 н.
0000264585 00000 н.
0000264740 00000 н.
0000264895 00000 н.
0000265049 00000 н.
0000265203 00000 н.
0000265650 00000 н.
0000265701 00000 п.
0000268535 00000 н.
0000269094 00000 н.
0000271188 00000 н.
0000271409 00000 н.
0000271459 00000 н.
0000271724 00000 н.
0000272693 00000 н.
0000273294 00000 н.
0000273345 00000 н.
0000273874 00000 н.
0000275197 00000 н.
0000275972 00000 н.
0000276023 00000 н.
0000276630 00000 н.
0000276830 00000 н.
0000276880 00000 н.
0000277115 00000 н.
0000277642 00000 н.
0000278179 00000 н.
0000278708 00000 н.
0000279240 00000 н.
0000279771 00000 н.
0000280301 00000 н.
0000280831 00000 н.
0000281363 00000 н.
0000281900 00000 н.
0000282434 00000 н.
0000282966 00000 н.
0000283500 00000 н.
0000284034 00000 н.
0000284567 00000 н.
0000285098 00000 н.
0000285164 00000 н.
0000285395 00000 н.
0000285510 00000 н.
0000285631 00000 н.
0000285778 00000 н.
0000285918 00000 н.
0000286150 00000 н.
0000286299 00000 н.
0000286480 00000 н.
0000286662 00000 н.
0000286821 00000 н.
0000287026 00000 н.
0000287205 00000 н.
0000287366 00000 п.
0000287516 00000 н.
0000287705 00000 н.
0000287864 00000 н.
0000288000 00000 н.
0000288138 00000 н.
0000288280 00000 н.
0000288420 00000 н.
0000288602 00000 н.
0000288766 00000 н.
0000288928 00000 н.
0000289102 00000 п.
0000289260 00000 н.
0000289428 00000 н.
0000289610 00000 н.
0000289784 00000 н.
0000289958 00000 н.
00002 00000 н.
00002 00000 н.
00002 00000 н.
00002 00000 н.
00002
00000 н. 00002 00000 н. 00002 00000 н. 00002
00000 н. 00002
00000 н. 0000200000 н. 00002
00000 н. 0000200000 н. 0000292562 00000 н. 0000292738 00000 н. 0000292918 00000 н. 0000293084 00000 н. 0000293252 00000 н. 0000293431 00000 н. 0000293596 00000 н. 0000293749 00000 н. 0000293922 00000 н. 0000294087 00000 н. 0000294294 00000 н. 0000294457 00000 н. 0000294632 00000 н. 0000294844 00000 н. 0000295012 00000 н. 0000295204 00000 н. 0000295360 00000 н. 0000295557 00000 н. 0000295719 00000 н. 0000295881 00000 н. 0000296091 00000 н. 0000296257 00000 н. 0000296455 00000 н. 0000296629 00000 н. 6 Uj @ d8: m / «yϻ &) B4B ߠ tXWf | Eq3 | x} չ 4 ꮷ (R̈́ \ ef: d Mu5 \ aa + o ~ ᕯ /> 09p` 1 & ř) K \ W2jm ֲ YQAnm-OO9agŬ @ rTXYLjpY,.w4 / 4Y * 7E3 [yeur0X} KC% WO97 *
Объяснение алгоритма опорных векторов (SVM)
Итак, вы работаете над проблемой классификации текста. Вы уточняете свои тренировочные данные и, возможно, даже экспериментировали с наивным байесовским методом. Вы уверены в своем наборе данных и хотите сделать еще один шаг вперед.
Введите Машины опорных векторов (SVM) , быстрый и надежный алгоритм классификации, который очень хорошо работает с ограниченным объемом данных для анализа.
Возможно, вы копнули немного глубже и столкнулись с такими терминами, как линейно отделимая , трюк ядра и функции ядра . Но не бойтесь! Идея, лежащая в основе алгоритма SVM, проста, и ее применение к NLP не требует большинства сложных вещей.
В этом руководстве вы узнаете основы SVM и научитесь использовать ее для классификации текста. Наконец, вы увидите, насколько легко начать работу с инструментом без кода, таким как MonkeyLearn.
Начните классификацию текста с помощью SVM
Что такое машины опорных векторов?
Машина опорных векторов (SVM) — это модель машинного обучения с учителем, которая использует алгоритмы классификации для задач классификации на две группы.После предоставления модели SVM наборов помеченных обучающих данных для каждой категории, они могут классифицировать новый текст.
По сравнению с более новыми алгоритмами, такими как нейронные сети, у них есть два основных преимущества: более высокая скорость и лучшая производительность при ограниченном количестве выборок (в тысячах). Это делает алгоритм очень подходящим для задач классификации текста, когда обычно имеется доступ к набору данных, состоящему максимум из пары тысяч помеченных образцов.
Как работает SVM?
Основы машин опорных векторов и принципы их работы лучше всего понять на простом примере.Представим, что у нас есть два тега: красный и синий , а наши данные имеют две характеристики: x и y . Нам нужен классификатор, который, учитывая пару координат (x, y) , выводит, будет ли это красный или синий . Мы наносим наши уже помеченные данные обучения на плоскость:
Наши помеченные данные
Машина опорных векторов берет эти точки данных и выводит гиперплоскость (которая в двух измерениях представляет собой просто линию), которая лучше всего разделяет теги.Эта линия является границей решения : все, что падает на одну сторону от нее, мы классифицируем как синий , а все, что падает на другую сторону как красный .
В 2D лучшая гиперплоскость — это просто линия
Но что именно является лучшей гиперплоскостью ? Для SVM это тот, который максимизирует поля для обоих тегов. Другими словами: гиперплоскость (помните, что в данном случае это линия), расстояние до ближайшего элемента каждого тега которой является наибольшим.
Не все гиперплоскости созданы одинаковыми
Вы можете посмотреть этот видеоурок, чтобы узнать, как именно находится эта оптимальная гиперплоскость.
Нелинейные данные
Теперь этот пример был легким, поскольку очевидно, что данные были линейно разделяемыми — мы могли провести прямую линию, чтобы разделить красный и синий . К сожалению, обычно все не так просто. Взгляните на этот случай:
Более сложный набор данных
Совершенно очевидно, что нет линейной границы принятия решений (единственной прямой линии, разделяющей оба тега).Однако векторы очень четко разделены, и похоже, что их должно быть легко разделить.
Итак, вот что мы сделаем: добавим третье измерение. До сих пор у нас было два измерения: x и y . Мы создаем новое измерение z и указываем, что оно должно быть вычислено определенным удобным для нас способом: z = x² + y² (вы заметите, что это уравнение для круга).
Это даст нам трехмерное пространство.Если взять кусочек этого пространства, это выглядит так:
С другой стороны, данные теперь разделены на две линейно разделенные группы
Что с этим может сделать SVM? Посмотрим:
Отлично! Обратите внимание, что, поскольку сейчас мы находимся в трех измерениях, гиперплоскость — это плоскость, параллельная оси x на некотором расстоянии z (допустим, z = 1 ).
То, что осталось, — это сопоставление его с двумя измерениями:
Вернемся к нашему исходному виду, теперь все аккуратно разделено
И вот мы! Граница нашего решения — это окружность радиуса 1, которая разделяет оба тега с помощью SVM.Посмотрите эту трехмерную визуализацию, чтобы увидеть еще один пример того же эффекта:
Уловка с ядром
В нашем примере мы нашли способ классификации нелинейных данных, грамотно сопоставив наше пространство с более высоким измерением. Однако оказывается, что вычисление этого преобразования может быть довольно затратным с точки зрения вычислений: может быть много новых измерений, каждое из которых, возможно, требует сложных вычислений. Выполнение этого для каждого вектора в наборе данных может потребовать больших усилий, поэтому было бы здорово, если бы мы могли найти более дешевое решение.
И нам повезло! Вот уловка: SVM не нужны реальные векторы, чтобы творить чудеса, на самом деле она может обойтись только скалярными произведениями между ними. Это означает, что мы можем обойти дорогостоящие расчеты новых размеров.
Это то, что мы делаем вместо этого:
Представьте себе новое пространство, которое мы хотим:
z = x² + y²
Выясните, как выглядит точечный продукт в этом пространстве:
a · b = xa · xb + ya · yb + za · zb
a · b = xa · xb + ya · yb + (xa² + ya²) · (xb² + yb²)
Скажите SVM сделать свое дело, но с использованием нового скалярного произведения — мы называем это функцией ядра .
Вот и все! Это трюк с ядром , который позволяет нам избежать множества дорогостоящих вычислений. Обычно ядро линейное, и мы получаем линейный классификатор. Однако, используя нелинейное ядро (как указано выше), мы можем получить нелинейный классификатор без преобразования данных вообще: мы меняем только скалярный продукт на то, что нам нужно, и SVM с радостью продолжит работу.
Обратите внимание, что трюк с ядром на самом деле не является частью SVM. Его можно использовать с другими линейными классификаторами, такими как логистическая регрессия.Машина опорных векторов заботится только о нахождении границы решения.
Использование SVM с классификацией естественного языка
Итак, мы можем классифицировать векторы в многомерном пространстве. Большой! Теперь мы хотим применить этот алгоритм для классификации текста, и первое, что нам нужно, это способ преобразовать кусок текста в вектор чисел, чтобы мы могли запускать с ними SVM. Другими словами, какие функции мы должны использовать для классификации текстов с помощью SVM?
Самый распространенный ответ — частота слов, как мы это делали в Наивном Байесе.Это означает, что мы рассматриваем текст как набор слов, и для каждого слова, которое появляется в этом пакете, у нас есть особенность. Ценность этой функции будет заключаться в том, насколько часто это слово встречается в тексте.
Этот метод сводится к подсчету того, сколько раз каждое слово встречается в тексте, и делению его на общее количество слов. Так, в предложении «Все обезьяны — приматы, но не все приматы — обезьяны» слово обезьяны имеет частоту 2/10 = 0,2, а слово , но имеет частоту 1/10 = 0.1.
Для более продвинутой альтернативы расчета частот мы также можем использовать TF-IDF.
Теперь, когда мы это сделали, каждый текст в нашем наборе данных представлен как вектор с тысячами (или десятками тысяч) измерений, каждое из которых представляет частоту одного из слов текста. Идеально! Это то, что мы скармливаем SVM для обучения. Мы можем улучшить это, используя методы предварительной обработки, такие как выделение слов, удаление стоп-слов и использование n-граммов.
Выбор функции ядра
Теперь, когда у нас есть векторы признаков, остается только выбрать функцию ядра для нашей модели.Все проблемы индивидуальны, и функция ядра зависит от того, как выглядят данные. В нашем примере наши данные были расположены в концентрических кругах, поэтому мы выбрали ядро, которое соответствовало этим точкам данных.
Учитывая это, что лучше всего для обработки естественного языка? Нужен ли нам нелинейный классификатор? Или данные линейно разделимы? Оказывается, лучше всего придерживаться линейного ядра. Почему?
В нашем примере у нас было две функции. Некоторые реальные применения SVM в других областях могут использовать десятки или даже сотни функций.Между тем, классификаторы NLP используют тысячи функций, поскольку они могут иметь до одного для каждого слова, которое появляется в данных обучения. Это немного меняет проблему: хотя использование нелинейных ядер может быть хорошей идеей в других случаях, наличие такого количества функций в конечном итоге приведет к тому, что нелинейные ядра будут перегружать данные. Следовательно, лучше всего просто придерживаться старого доброго линейного ядра, которое на самом деле дает лучшую производительность в этих случаях.
Собираем все вместе
Теперь осталось только потренироваться! Мы должны взять наш набор помеченных текстов, преобразовать их в векторы с использованием частот слов и передать их алгоритму, который будет использовать нашу выбранную функцию ядра, чтобы он создал модель.Затем, когда у нас есть новый немаркированный текст, который мы хотим классифицировать, мы конвертируем его в вектор и передаем его модели, которая выведет тег текста.
Учебное пособие по простому классификатору SVM
Чтобы создать свой собственный классификатор SVM, не прибегая к векторам, ядрам и TF-IDF, вы можете сразу же использовать одну из предварительно созданных моделей классификации MonkeyLearn. Также легко создать свой собственный, благодаря интуитивно понятному пользовательскому интерфейсу платформы и подходу без кода.
Это также отлично подходит для тех, кто не хочет вкладывать большие средства в найм экспертов по машинному обучению.
Давайте покажем вам, как легко создать классификатор SVM за 8 простых шагов. Прежде чем начать, вам нужно зарегистрироваться в MonkeyLearn бесплатно.
1. Создайте новый классификатор
Перейдите на панель управления, нажмите «Создать модель» и выберите «Классификатор».
2. Выберите способ классификации данных
Мы собираемся выбрать модель «Тематическая классификация» для классификации текста по теме, аспекту или релевантности.
3. Импортируйте данные для обучения
Выберите и загрузите данные, которые вы будете использовать для обучения модели. Имейте в виду, что классификаторы учатся и становятся умнее, когда вы вводите им больше обучающих данных. Вы можете импортировать данные из файлов CSV или Excel.
4. Определите теги для классификатора SVM
Пришло время определить теги, которые вы будете использовать для обучения классификатора тем. Для начала добавьте как минимум два тега — вы всегда можете добавить другие теги позже.
5. Пометьте данные для обучения классификатора
Начните обучение классификатора тем, выбирая теги для каждого примера:
После добавления тегов к некоторым примерам вручную классификатор начнет делать прогнозы самостоятельно.Если вы хотите, чтобы ваша модель была более точной, вам нужно будет добавить теги к другим примерам, чтобы продолжить обучение модели.
Чем больше данных вы пометите, тем умнее будет ваша модель.
6. Установите свой алгоритм на SVM
Перейдите в настройки и убедитесь, что вы выбрали алгоритм SVM в расширенном разделе.
7. Проверьте свой классификатор
Теперь вы можете протестировать свой классификатор SVM, нажав «Выполнить»> «Демо». Напишите свой собственный текст и посмотрите, как ваша модель классифицирует новые данные:
8.Интегрируйте тематический классификатор
Вы научили свою модель делать точные прогнозы при классификации текста. Пришло время загрузить новые данные! Есть три разных способа сделать это с помощью MonkeyLearn:
Пакетная обработка: перейдите в «Выполнить»> «Пакетная обработка» и загрузите файл CSV или Excel. Классификатор проанализирует ваши данные и отправит вам новый файл с прогнозами.
API: используйте MonkeyLearn API для классификации новых данных из любого места.
Интеграции: подключайте повседневные приложения для автоматического импорта новых текстовых данных в ваш классификатор. Такие интеграции, как Google Sheets, Zapier и Zendesk, можно использовать без ввода единственной строчки кода:
Заключительные слова
И это основы машин поддерживающих векторов!
Подводя итог:
- Машина опорных векторов позволяет классифицировать данные, которые можно линейно разделить.
- Если он не разделен линейно, вы можете использовать трюк с ядром, чтобы заставить его работать.
- Однако для классификации текста лучше придерживаться линейного ядра.
С такими инструментами MLaaS, как MonkeyLearn, чрезвычайно просто реализовать SVM для классификации текста и сразу получить полезную информацию.
Создайте свой собственный классификатор SVM
Есть вопросы? Запланируйте демонстрацию, и мы поможем вам начать работу.
Машины опорных векторов для начинающих
Целевая функция первичной задачи отлично работает с линейно разделяемым набором данных, однако не решает нелинейный набор данных.В этой статье «Машины опорных векторов для начинающих — проблема двойственности » мы углубимся в преобразование первичной задачи в двойную задачу и решение целевых функций с помощью квадратичного программирования. Не волнуйтесь, если это звучит слишком сложно, я объясню концепции шаг за шагом.
Краткое описание
Мы прошли через понимание опорных векторов и полей . Затем использовал эти концепции для создания целевых функций для классификатора жесткой и мягкой маржи в нашем последнем руководстве.Tx_i + b) \ geq 1 — \ xi_i, \ text {где} \ xi_i \ geq 0 \ end {align}
Вот несколько важных моментов, которые следует запомнить из последнего урока,
- Используйте обучающие данные для определения оптимального геометрического поля, чтобы мы могли идентифицировать опорные векторы.
- Введена переменная Slack и определена целевая функция для классификатора Soft Margin.
- Преобразуйте ограничение неравенства в ограничение равенства, чтобы мы использовали градиентный спуск.
Если вам нужно обратиться к предыдущему руководству, вот ссылка
Первобытная проблема
Primal Problem помогает при решении Linear SVM с использованием SGD.Помните, что нам нужно оптимизировать параметры D + 1 (где D — измерение) в Primal Problem.
Однако наша конечная цель — решить нелинейную SVM, где основная задача бесполезна. Чтобы найти решение, нам нужно использовать несколько математических уловок. Мы пройдем их все по порядку.
Двойственность
В математической теории оптимизации, двойственность означает, что проблемы оптимизации могут рассматриваться с двух точек зрения: первичная проблема или двойная проблема ( принцип двойственности ).Решение двойственной задачи дает нижнюю оценку решения прямой (минимизационной) задачи.
Википедия
Я собираюсь объяснить очень просто, чтобы вы могли понять, не имея сильной математической подготовки.
- Первичная проблема — это то, что мы хотим минимизировать. На диаграмме P * минимизирует первичную цель P .
- Двойная проблема — это то, что мы хотим максимизировать.* = 0 $
- Далее мы поговорим о множителе Лагранжа , который поможет нам определить, когда мы можем найти сильную двойственность.
Мы можем найти максимум или минимум функции многих переменных с некоторым ограничением, используя множитель Лагранжа . Важно понимать множитель Лагранжа для решения задач оптимизации ограничений , как и в SVM.
Если вы помните нашу целевую функцию, у нас есть одно ограничение, такое что $ y_i (\ beta ^ Tx_i + b) \ geq 1 — \ xi_i $ для целевой функции,
\ begin {align} \ min _ {\ beta, b, \ xi_i} \ Big \ {\ frac {|| \ beta ^ 2 ||} {2} + C \ sum_ {i = 1} ^ n (\ xi_i) ^ k \ Big \ } \ end {align}
Концепции
Начнем с обобщенной версии.Давайте узнаем, как решить такую проблему, как:
\ begin {align} \ max_ {x, y} f (x, y) \\ \ text {такой, что} g (x, y) = c \ end {align}
Обратитесь к графику ниже, где функция f (x, y) была представлена с использованием контурного графика (поверхность), а g (x, y) отображена линией (зеленой).
В случае, если у нас не было ограничения g (x, y) , мы могли бы просто взять производную f (x, y) по x и y , а затем установить их на 0 , чтобы найти решение для x и y .
Однако теперь у нас есть ограничение, заданное функцией g (x, y) (представлено зеленой линией). Следовательно, нам нужно найти точку на зеленой кривой, для которой f (x, y) является максимальным.
Обратите внимание, что решением является точка, в которой f (x, y) и g (x, y) оба являются параллелью (выделено желтым кружком). Математически векторы градиента в этой точке касания ориентированы в одном направлении.
Мы собираемся ввести новую переменную $ \ alpha $ как Множитель Лагранжа .Затем выразите следующее как функцию с именем Lagrangian.
\ begin {align} L (х, у, \ альфа) = е (х, у) — \ альфа \ большой (г (х, у) — с \ большой) \ end {align}
Решение состоит в том, чтобы найти $ (x, y, \ alpha) $ так, чтобы $ \ Delta L = 0 $
\ begin {align} \ delta_ {x, y, \ alpha} L (x, y, \ alpha) = 0 \ end {align}
Давайте сначала возьмем частную производную по t $ \ alpha $
\ begin {align} \ delta _ {\ alpha} L (x, y, \ alpha) = & \ frac {d} {d \ alpha} \ bigg (f (x, y) — \ alpha \ Big (g (x, y) — c \ Большой) \ bigg) \\ = & — \ Большой (g (x, y) -c \ Big) \ end {align}
Следовательно, мы можем сказать, что
\ begin {align} \ delta _ {\ alpha} L (x, y, \ alpha) = & — g (x, y) + c = 0 \ end {align}
Мы также можем взять частную производную w.r.t x
\ begin {align} \ delta _ {\ alpha} L (x, y, \ alpha) = & \ frac {d} {d \ alpha} \ bigg (f (x, y) — \ alpha \ Big (g (x, y) — c \ Большой) \ bigg) = 0 \\ \ delta_x f (x, y) — \ alpha \ delta_x g (x, y) = & 0 \\ \ delta_x f (x, y) = & \ alpha \ delta_x g (x, y) \ end {align}
Аналогично
\ begin {align} \ delta_y f (x, y) = & \ alpha \ delta_y g (x, y) \ end {align}
Мы можем записать их с помощью одного уравнения,
\ begin {align} \ delta_ {x, y} f (x, y) = & \ alpha \ delta_ {x, y} g (x, y) \ end {align}
Это соответствует идее, что $ \ delta f (x, y) $ и $ \ delta g (x, y) $ оба указывают на одинаковое направление в решении (желтый кружок).Это означает, что градиенты действительно параллельны .
Обратите внимание: даже если они указывают в одном направлении, они могут иметь разную величину , поэтому градиент g (x, y) масштабируется на $ \ alpha $
.Теперь у нас есть 3 уравнения и 3 неизвестных. Мы легко можем их решить.
Если вы зашли так далеко и вышеупомянутая идея не имела особого смысла, не волнуйтесь, закончите всю статью и прочтите еще несколько раз, и все начнет обретать смысл.2 = 1 $ красным, это круг.
- $ x + y $ должен находиться на круге в соответствии с определенным ограничением.
- Мы можем визуально идентифицировать две точки (среди всех точек), где значение $ x + y $ должно касаться круга в двух разных точках.
- Эти точки представляют собой максимальное и минимальное значения.
Теперь давайте воспользуемся множителем Лагранжа , чтобы решить это математически.2} & = 1 \\ \ alpha & = \ pm \ frac {1} {\ sqrt {2}} \ end {align}
Используя это, мы можем получить значения x и y .
\ begin {align} x & = \ pm \ frac {1} {2 \ frac {1} {\ sqrt {2}}} \\ x & = \ frac {1} {\ sqrt {2}} \\ \ text {аналогично} \\ y & = \ frac {1} {\ sqrt {2}} \ end {align}
Поскольку мы связываем, чтобы максимизировать $ x + y $, мы будем рассматривать только положительные значения.
Итак, у нас есть окончательный результат как,
\ begin {align} е (х, у) = & х + у \\ = & \ frac {1} {\ sqrt {2}} + \ frac {1} {\ sqrt {2}} \\ = & \ sqrt {2} \ end {align}
Множественные ограничения
Множитель Лагранжа также может использоваться для векторизации.Предположим, что x имеет D размеров, тогда всего будет D + 1 неизвестных для следующей функции,
\ begin {align} \ max_x f (x) \\ \ text {s.t. } g (x) = 0 \ end {align}
У вас также может быть несколько ограничений. Если у вас есть n ограничений, то всего будет D + n неизвестных. n \ alpha_i g_i (x)
\ end {align}
Ограничение неравенства
Множитель Лагранжа также работает с ограничениями неравенства.m \ lambda_j h_j (x) \\ \ end {align}
Однако, чтобы найти решение для переменных, недостаточно просто взять градиенты и установить их равными нулю из-за ограничений неравенства.
Установка $ \ Delta_ {x, \ lambda} L = 0 $ по-прежнему дает два условия, но для ограничения неравенства нам нужно иметь 3 дополнительных условия. Следовательно, вместо трех, у нас будет всего 5 условий.
\ begin {align} \ alpha_i g_i (x) = & 0 \ text {,} \ forall i = 1..n \\ g_i (x) \ leq & 0 \ text {,} \ forall i = 1..n \\ \ alpha_i \ geq & 0 \ text {,} \ forall i = 1..n \\ \ delta_ {x_d} L = & 0 \ text {,} \ forall d = 1..D \\ \ delta _ {\ lambda_j} L = & 0 \ text {,} \ forall j = 1..m \\ \ end {align}
Сильная двойственность
Условия KKT
Эти пять вышеупомянутых условий называются условиями KKT (Каруш – Куна – Такера), и они должны выполняться для сильной двойственности , т.е.Tx_i + b) \ geq 1 $, что означает, что если точка не является опорным вектором, то $ \ alpha_i = 0 $
Две вышеупомянутые интуиции важны, это указывает на то, что не поддерживающие векторы не играют роли в определении веса и смещения.
Когда мы знаем $ \ alpha_i $ для всех точек, мы можем вычислить весовой вектор $ \ beta $, суммируя только опорные векторы.
\ begin {align} \ beta = \ sum_ {i, \ alpha_i \ geq 0} \ alpha_i y_ix_i \ end {align}
Чтобы вычислить смещение b , нам нужно получить одно решение $ b_i $ для каждого вектора поддержки, а затем усреднить их.п \ alpha_i y_i = 0 \ end {align}
Обратите внимание, что целевая функция такая же, как у классификатора жесткой маржи, однако ограничение неравенства другое.
Поскольку $ \ alpha_i + \ lambda_i = C $ и $ \ alpha_i \ geq 0, \ lambda_i \ geq 0 $, мы можем сказать $ 0 \ leq \ alpha_i \ leq 0 $. На $ \ lambda $ нет ограничений, поскольку он не является частью окончательного уравнения.
Вектор веса и смещение
Подобно классификатору жесткой маржи, мы можем получить вектор веса из векторов поддержки, как и раньше.Теперь опорные векторы включают в себя все точки, которые находятся на марже (Zero Slack $ \ xi_i = 0 $), а также все точки с положительным Slack $ \ xi_i> 0 $
\ begin {align} \ beta = \ sum_ {i, \ alpha_i \ geq 0} \ alpha_i y_ix_i \ end {align}
Теперь мы можем решить для $ \ xi_i $,
\ begin {align} \ lambda_i (0- \ xi_i) = & 0 \\ (C — \ alpha_i) (0- \ xi_i) = & 0, [\ lambda_i \ text {из условия KKT}] \\ \ xi_i (C — \ alpha_i) = & 0 \\ \ end {align}
Теперь у нас есть два случая для опорных векторов с $ \ alpha_i> 0 $
- Если $ \ xi_i> 0 $, то $ (C- \ alpha_i) = 0 $.Tx_j $ как внутренний продукт для достижения нелинейности. Это основная причина, по которой мы провели все эти вычисления только для определения целевой функции.
В следующем уроке мы вкратце узнаем о ядре и используем его в SVM Dual Problem.
Об авторе