Формула pv: Понятие, формула дисконтирования | Таблица дисконтирования
Понятие, формула дисконтирования | Таблица дисконтирования
Знаете ли вы, что означает дисконтирование? Если вы читаете эту статью, значит, вы уже слышали это слово. И если вы пока не поняли до конца, что это такое, то эта статья для вас. Даже если вы не собираетесь сдавать экзамен Дипифр, а просто хотите разобраться в этом вопросе, прочитав эту статью, вы сможете прояснить для себя понятие дисконтирования.
Данная статья доступным языком рассказывает о том, что такое дисконтирование. На простых примерах в ней показана техника расчета дисконтированной стоимости. Вы узнаете, что такое фактор дисконтирования и научитесь пользоваться таблицами коэффициентов дисконтирования.
Понятие и формула дисконтирования доступным языком
Чтобы проще было объяснить понятие дисконтирования, начнём с другого конца. А точнее, возьмем пример из жизни, знакомый каждому.
Пример 1. Представьте, что вы пришли в банк и решили сделать вклад в размере 1000 долларов.
Через два года нынешние 1000 долларов превратятся в $1210 ($1000 плюс проценты за первый год $100 плюс проценты за второй год $110=1100*10%). Общая формула приращения вклада за два года: (1000*1,10)*1,10 = 1210
С течением времени величина вклада будет расти и дальше. Чтобы узнать, какая сумма вам причитается от банка через год, два и т.д., надо сумму вклада умножить на множитель: (1+R)n
- где R – ставка процента, выраженная в долях от единицы (10% = 0,1)
- N – число лет
В данном примере 1000*(1,10)2 = 1210. Из формулы очевидно (да и из жизни тоже), что сумма вклада через два года зависит от банковской ставки процента.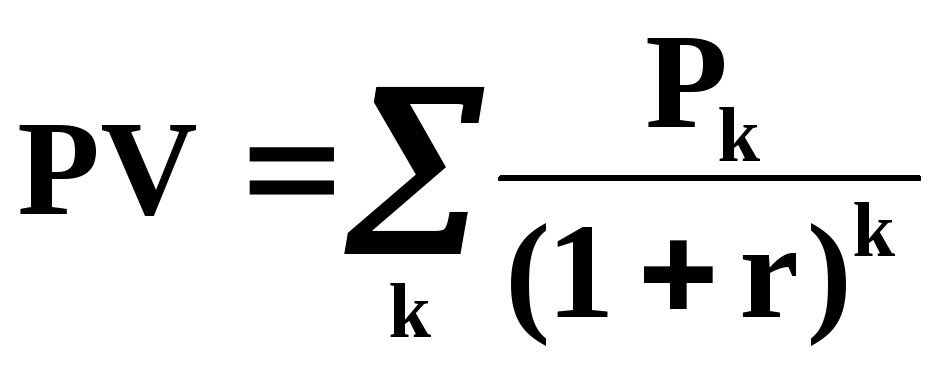
Таким способом можно рассчитать величину вашего вклада в любой момент времени в будущем. Расчет будущей стоимости денег в английском языке называется «compounding». Данный термин на русский язык переводят как «наращение» или калькой с английского как «компаундирование». Лично мне больше нравится перевод данного слова как «приращение» или «прирост».
Смысл понятен – с течением времени денежный вклад увеличивается за счет приращения (прироста) ежегодными процентами. На этом, собственно говоря, построена вся банковская система современной (капиталистической) модели мироустройства, в которой время – это деньги.
Теперь давайте посмотрим на данный пример с другого конца. Допустим, вам нужно отдать долг своему приятелю, а именно: через два года заплатить ему $1210. Вместо этого вы можете отдать ему $1000 сегодня, а ваш приятель положит эту сумму в банк под годовую ставку 10% и через два года снимет с банковского вклада ровно необходимую сумму $1210. То есть эти два денежных потока: $1000 сегодня и $1210 через два года — эквивалентны друг другу. Не важно, что выберет ваш приятель – это две равноценные возможности.
Вместо этого вы можете отдать ему $1000 сегодня, а ваш приятель положит эту сумму в банк под годовую ставку 10% и через два года снимет с банковского вклада ровно необходимую сумму $1210. То есть эти два денежных потока: $1000 сегодня и $1210 через два года — эквивалентны друг другу. Не важно, что выберет ваш приятель – это две равноценные возможности.
ПРИМЕР 2. Допустим, через два года вам надо сделать платёж в сумме $1500. Чему эта сумма будет равноценна сегодня?
Чтобы рассчитать сегодняшнюю стоимость, нужно идти от обратного: 1500 долларов разделить на (1,10)2 , что будет равно примерно 1240 долларам. Этот процесс и называется дисконтированием.
Если говорить простым языком, то дисконтирование – это определение сегодняшней стоимости будущей денежной суммы (или если говорить более правильно, будущего денежного потока).
Если вы хотите выяснить, сколько будет стоить сегодня сумма денег, которую вы или получите, или планируете потратить в будущем, то вам надо продисконтировать эту будущую сумму по заданной ставке процента. Эта ставка называется «ставкой дисконтирования». В последнем примере ставка дисконтирования равна 10%, 1500 долларов – это сумма платежа (денежного оттока) через 2 года, а 1240 долларов – это и есть так называемая дисконтированная стоимость будущего денежного потока. В английском языке существуют специальные термины для обозначения сегодняшней (дисконтированной) и будущей стоимости: future value (FV) и present value (PV). В примере выше $1500 — это будущая стоимость FV, а $1240 – это текущая стоимость PV.
Эта ставка называется «ставкой дисконтирования». В последнем примере ставка дисконтирования равна 10%, 1500 долларов – это сумма платежа (денежного оттока) через 2 года, а 1240 долларов – это и есть так называемая дисконтированная стоимость будущего денежного потока. В английском языке существуют специальные термины для обозначения сегодняшней (дисконтированной) и будущей стоимости: future value (FV) и present value (PV). В примере выше $1500 — это будущая стоимость FV, а $1240 – это текущая стоимость PV.
Когда мы дисконтируем — мы идём от будущего к сегодняшнему дню.
Дисконтирование
Когда мы наращиваем — мы идём от сегодняшнего дня в будущее.
Наращение
Формула для расчета дисконтированной стоимости или формула дисконтирования для данного примера имеет вид: 1500 * 1/(1+R)n = 1240.
Математическая формула дисконтирования в общем случае будет такая: FV * 1/(1+R)n = PV. Обычно её записывают в таком виде:
Обычно её записывают в таком виде:
PV = FV * 1/(1+R)n
Коэффициент, на который умножается будущая стоимость 1/(1+R)nназывается фактором дисконтирования от английского слова factor в значении «коэффициент, множитель».
В данной формуле дисконтирования: R – ставка процента, N – число лет от даты в будущем до текущего момента.
Таким образом:
- Compounding или Приращение – это, когда вы идете от сегодняшней даты в будущее.
- Discounting или Дисконтирование – это, когда вы идете из будущего к сегодняшнему дню.
Обе «процедуры» позволяют учесть эффект изменения стоимости денег с течением времени.
Конечно, все эти математические формулы сразу наводят тоску на обычного человека, но главное, запомнить суть. Дисконтирование – это когда вы хотите узнать сегодняшнюю стоимость будущей суммы денег (которую вам надо будет потратить или получить).
Надеюсь, что теперь, услышав фразу «понятие дисконтирования», вы сможете объяснить любому, что подразумевается под этим термином.
Приведенная стоимость – это дисконтированная стоимость?
В предыдущем разделе мы выяснили, что
Дисконтирование– это определение текущей стоимости будущих денежных потоков.
Не правда ли, в слове «дисконтирование» слышится слово «дисконт» или по-русски скидка? И действительно, если посмотреть на этимологию слова discount, то уже в 17 веке оно использовалось в значении «deduction for early payment», что означает «скидка за раннюю оплату». Уже тогда много лет назад люди учитывали временную стоимость денег. Таким образом, можно дать еще одно определение: дисконтирование – это расчет скидки за быструю оплату счетов. Эта «скидка» и является мерилом временной стоимости денег или time value of money.
Дисконтированная стоимость – это текущая стоимость будущего денежного потока (т.е. будущий платеж за вычетом «скидки» за быструю оплату). Ее еще называют приведенной стоимостью, от глагола «приводить». Говоря простыми словами, приведенная стоимость – это будущая денежная сумма, приведенная к текущему моменту.
Если быть точным, то дисконтированная и приведенная стоимость – это не абсолютные синонимы. Потому что приводить можно не только будущую стоимость к текущему моменту, но и текущую стоимость к какому-то моменту в будущем. Например, в самом первом примере можно сказать, что 1000 долларов, приведенные к будущему моменту (через два года) при ставке 10% равны 1210 долларов. То есть, я хочу сказать, что приведенная стоимость – это более широкое понятие, чем дисконтированная стоимость.
Кстати, в английском языке такого термина (приведенная стоимость) нет. Это наше, чисто русское изобретение. В английском языке есть термин present value (текущая стоимость) и discounted cash flows (дисконтированные денежные потоки). А у нас есть термин приведенная стоимость, и он чаще всего используется именно в значении «дисконтированная» стоимость.
Таблица дисконтирования
Чуть выше я уже приводила формулу дисконтирования PV = FV * 1/(1+R)n, которую можно описать словами как:
Дисконтированная стоимость равна будущая стоимость, умноженная на некий множитель, который называется фактором дисконтирования.
Коэффициент дисконтирования 1/(1+R)n, как видно из самой формулы, зависит от ставки процента и количества периодов времени. Чтобы не вычислять его каждый раз по формуле дисконтирования, пользуются таблицей, показывающей значения коэффициента в зависимости от % ставки и количества периодов времени. Иногда она называется «таблица дисконтирования», хотя это не совсем правильный термин. Это таблица коэффициентов дисконтирования, которые рассчитываются, как правило, с точностью до четвертого знака после запятой.
Пользоваться данной таблицей коэффициентов дисконтирования очень просто: если вы знаете ставку дисконтирования и число периодов, например, 10% и 5 лет, то на пересечении соответствующих столбцов находится нужный вам коэффициент.
Пример 3. Давайте разберем простой пример. Допустим, вам нужно выбрать между двумя вариантами:
- А) получить 100,000 долларов сегодня
- Б) или 150,000 долларов одной суммой ровно через 5 лет
Что выбрать?
Если вы знаете, что банковская ставка по 5-летним депозитам составляет 10%, то вы легко можете посчитать, чему равна сумма 150,000 долларов к получению через 5 лет, приведенная к текущему моменту.
Соответствующий коэффициент дисконтирования в таблице равен 0,6209 (ячейка на пересечении строки 5 лет и столбца 10%). 0,6209 означает, что 62,09 цента, полученные сегодня, равны 1 доллару к получению через 5 лет (при ставке 10%). Простая пропорция:
сегодня | через 5 лет |
62,09 цента | $1 |
X? | 150,000 |
Таким образом, $150,000*0,6209 = 93,135.
93,135 — это дисконтированная (приведенная) стоимость суммы $150,000 к получению через 5 лет.
Она меньше, чем 100,000 долларов сегодня. В данном случае, синица в руках действительно лучше, чем журавль в небе. Если мы возьмем 100,000 долларов сегодня, положим их на депозит в банке по 10% годовых, то через 5 лет мы получим: 100,000*1,10*1,10*1,10*1,10*1,10 = 100,000*(1,10)5 = 161,050 долларов. Это более выгодный вариант.
Это более выгодный вариант.
Чтобы упростить это вычисление (вычисление будущей стоимости при заданной сегодняшней стоимости), можно также воспользоваться таблицей коэффициентов. По аналогии с таблицей дисконтирования эту таблицу можно назвать таблицей коэффициентов приращения (наращения). Вы можете построить такую таблицу самостоятельно в Excele, если используете формулу для расчета коэффициента приращения:(1+R)n.
Из этой таблицы видно, что 1 доллар сегодня при ставке 10% через 5 лет будет стоить 1,6105 долларов.
С помощью такой таблицы легко будет посчитать, сколько денег нужно положить в банк сегодня, если вы хотите получить определенную сумму в будущем (не пополняя вклад). Чуть более сложная ситуация возникает, когда вы хотите не только положить деньги на депозит сегодня, но и собираетесь каждый год добавлять определенную сумму к своему вкладу. Как это рассчитать, читайте в следующей статье. Она называется формула аннуитета.
Философское отступление для тех, кто дочитал до этого места
Дисконтирование базируется на знаменитом постулате «время — деньги». Если задуматься, то эта иллюстрация имеет очень глубокий смысл. Посадите яблоню сегодня, и через несколько лет ваша яблоня вырастет, и вы будете собирать яблоки в течение многих лет. А если сегодня вы не посадите яблоню, то в будущем яблок вы так и не попробуете.
Если задуматься, то эта иллюстрация имеет очень глубокий смысл. Посадите яблоню сегодня, и через несколько лет ваша яблоня вырастет, и вы будете собирать яблоки в течение многих лет. А если сегодня вы не посадите яблоню, то в будущем яблок вы так и не попробуете.
Всё, что нам нужно – это решиться: посадить дерево, начать свое дело, стать на путь, ведущий к исполнению мечты. Чем раньше мы начнем действовать, тем больший урожай мы получим в конце пути. Нужно превращать время, отпущенное нам в нашей жизни, в результаты.
«Семена цветов, которые распустятся завтра, сажают сегодня». Так говорят китайцы.
Если вы мечтаете о чем-то, не слушайте тех, кто вас отговаривает или подвергает сомнению ваш будущий успех. Не ждите удачного стечения обстоятельств, начинайте как можно раньше. Превращайте время вашей жизни в результаты.
Большая таблица коэффициентов дисконтирования (открывается в новом окне):
Вы можете прочитать другие статьи по теме Финансы:
1. Капитализация вклада — что это? Формула капитализации процентов: ежемесячно, ежедневно, непрерывно.
Капитализация вклада — что это? Формула капитализации процентов: ежемесячно, ежедневно, непрерывно.
Рассчитать свой потенциальный доход по вкладу можно самостоятельно, не полагаясь на калькуляторы дохода, которые размещены на сайтах банковских учреждений. В этой статье на конкретных примерах показано, как рассчитать доход по вкладу с капитализацией процентов (ежеквартальной, ежемесячной) и как рассчитать эффективную ставку по вкладам с капитализацией.
2. Формула аннуитета. Вечная рента. Это надо знать каждому! (не для банкиров)
Вечная рента — это серия одинаковых платежей, которые продолжаются вечно. Такой вариант возможен, если, например, у вас есть вклад в банке, вы снимаете только ежегодные проценты, а основная сумма вклада остается нетронутой. Тогда, если ставка процента по вкладу не меняется, у вас будет так называемая вечная рента.
3. Формула расчета NPV инвестиционного проекта. Это просто.
Инвестировать — это значит вложить свободные финансовые ресурсы сегодня с целью получения стабильных денежных потоков в будущем.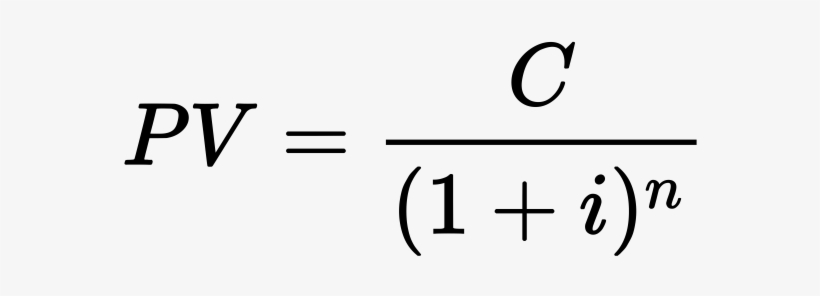 Как не ошибиться и не только вернуть вложенные средства, но еще и получить прибыль от инвестиций?
Как не ошибиться и не только вернуть вложенные средства, но еще и получить прибыль от инвестиций?
4. Внутренняя норма доходности. Формула расчета IRR инвестиционного проекта
В данной статье приведены не только формула и определение IRR, но есть примеры расчетов этого показателя (в Excel, графический) и интерпретации полученных результатов. Два примера из жизни, с которыми сталкивается каждый человек
5. Ставка дисконтирования для инвестиционного проекта. Это WACC — средневзвешенная стоимость капитала.
По своей сути ставка дисконтирования при анализе инвестиционных проектов — это ставка процента, по которой инвестор привлекает финансирование. Как ее рассчитать?
Самые интересные статьи по теме МСФО и Дипифр:
1. Консолидация — это контроль. МСФО IFRS 10 — это единая концепция контроля для любых объединений бизнеса
2. Как сдать экзамен Дипифр со второго раза?
Перейти на главную страницу
CFA — Как рассчитывать текущую (приведенную) стоимость денежного потока (PV)? | программа CFA
См. начало:
начало:
Фактор будущей стоимости связывает сегодняшнюю текущую (приведенную) стоимость (PV, англ. ‘present value’) денежного потока с его будущей стоимостью (FV, англ. ‘future value’). Этот коэффициент позволяет рассчитать как FV, так и PV.
Например, 5-процентная ставка приносит будущий доход в размере $105 за 1 год.
Какой должна быть текущая (первоначальная) сумма, вложенная под 5%, чтобы она выросла до $105 через 1 год?
Ответ: $100 представляют собой текущую стоимость (PV) для будущей суммы (FV) в размере $105, которая должна быть получена через 1 год, при ставке вклада 5%.
Используя будущий денежный поток, который должен быть получен в течение N периодов, и процентную ставку за период r, мы можем преобразовать формулу (2) будущей стоимости денежного потока следующим образом:
FVN = PV * (1 + r)N
\( \mathbf { PV=FV_N \left[ 1 \over (1+r)^N \right] }\)
PV = FVN * [1 / (1 + r)N] (формула 8)
или
PV = FVN * (1 + r)-N
Из формулы 8 видно, что фактор текущей стоимости (англ. ‘present value factor’), (1 + r)-N является обратной величиной фактора будущей стоимости (1 + r)N.
‘present value factor’), (1 + r)-N является обратной величиной фактора будущей стоимости (1 + r)N.
Пример расчета текущей стоимости денежного потока.
Страховая компания выпустила гарантированный инвестиционный сертификат (GIC), который гарантирует выплату $100 000 в течение 6 лет с 8-процентной прибылью.
Какую сумму страховщик должен инвестировать сегодня, чтобы через 6 лет обеспечить выплату обещанной суммы по сертификату?
Решение:
Мы можем применить формулу 8, чтобы найти текущую (приведенную) стоимость, используя следующие данные:
FVN = $100,000
r = 8% = 0.08
N = 6
PV = FVN (1 + r)-N
= $100,000 * [1 / (1.0 8)6]
= $100,000 * (0.6301696) = $63,016.96
Можно сказать, что сегодня $63 016,96 при процентной ставке 8% эквивалентны $100 000, которые будут получены через 6 лет.
Дисконтирование сегодняшней суммы $100 000 делает будущую сумму в размере $100 000 эквивалентом $63 016,96, с учетом временной стоимости денег (TVM).
Как показывает временная линия на рисунке ниже, $100 000 дисконтированы в течение 6 полных периодов.
Текущая стоимость (PV) $100 000 в момент времени t = 6.
Пример прогнозирования текущей стоимости денежного потока.
Предположим, что у вас есть ликвидный финансовый актив, который принесет вам $100 000 через 10 лет от текущей даты.
Ваша дочь планирует поступить в колледж через четыре года, и вы хотите знать, какова будет текущая (приведенная) стоимость актива к этому моменту.
С учетом 8% ставки дисконтирования, какова будет стоимость актива через 4 года от текущей даты?
Решение:
Стоимость актива ($100 000) — это текущая стоимость через 10 лет. При t = 4 эта сумма будет получена 6 лет спустя — см. рисунок ниже.
Связь между текущей и будущей стоимостью актива.
С помощью этой информации вы можете вычислить стоимость актива через 4 года от текущей даты, используя формулу 8:
FVN = $100,000
r = 8% = 0.08
N = 6
PV = FVN (1 + r)-N
= $100,000 * [1 / (1.08)6]
= $100,000 * (0.6301696)
= $63,016.96
Временная линия на рисунке выше показывает будущий платеж в размере $100 000, который должен быть получен при t = 10. На временной шкале также показана стоимость денежного потока при t = 4 и при t = 0.
По сравнению с суммой при t = 10, сумма при t = 4 представляет собой прогнозируемую текущую стоимость, а сумма при t = 0 является текущей приведенной стоимостью (на сегодняшний день).
Задачи, требующие вычисления текущей стоимости (PV) требуют определения фактора текущей стоимости
(1 + r)-N.
Текущая стоимость зависит от процентной ставки и количества периодов начисления процентов следующим образом:
- При заданной ставке дисконтирования, чем дальше в будущем будет получена сумма, тем меньше будет текущая стоимость (PV) этой суммы.

- Для одного и того же момента времени, с ростом ставки дисконтирования уменьшается текущая стоимость будущей суммы.
Расчет текущей (приведенной) стоимости с промежуточным начислением процентов.
Напомним, что проценты могут выплачиваться раз в полгода, ежеквартально, ежемесячно или даже ежедневно.
Для расчета процентных платежей, производимых более 1 раза в год, мы можем изменить формулу текущей стоимости (8).
Напомним, что rS — котируемая (заявленная) процентная ставка и она равна периодической процентной ставке, умноженной на количество периодов начисления в каждом году.
В целом, если в году есть более 1 промежуточного периода начисления, мы можем выразить формулу расчета текущей стоимости (PV) как:
PV = FVN * (1 + rS/m)-mN (формула 9)
где:
m = количество периодов начисления в году,
rS = заявленная годовая процентная ставка,
N = количество лет.
Формула 9 очень похожа на формулу 8.
Как мы уже отмечали, фактор текущей стоимости и фактор будущей стоимости являются обратными значениями по отношению друг к другу. И добавление в формулу частоты начисления процентов не влияет на эту взаимозависимость между двумя факторами.
Единственное различие заключается в использовании периодической процентной ставки и соответствующего количества периодов начисления.
Следующий пример иллюстрирует формулу 9.
Пример расчета текущей (приведенной) стоимость при ежемесячном начислении процентов.
Менеджер канадского пенсионного фонда знает, что фонд должен выполнить единовременный платеж в размере $5 млн. через 10 лет. Она планирует сегодня инвестировать некоторую сумму в гарантированный инвестиционный сертификат (GIC), чтобы эта инвестиция выросла до необходимой суммы в $5 млн.
Текущая процентная ставка по GIC составляет 6 процентов в год, с ежемесячным начислением процентов.
Сколько она должна сегодня инвестировать в GIC?
Решение:
Используя формулу 9, чтобы находим требуемую текущую стоимость:
FVN = $5,000,000
rS = 6% = 0.06
m = 12
rS / m = 0.06/12 = 0.005
N = 10
mN = 12*(10) = 120
PV = FVN * (1 + rS/m)-mN
= $5,000,000 * (1.005)-120
= $5,000,000 * (0.549633)
= $2,748,163.67
При применении формулы 9 мы используем периодическую ставку (в данном случае, месячную ставку) и соответствующее количество периодов с ежемесячным начислением процентов (в данном случае 10 лет ежемесячных начислений или 120 периодов).
См. далее:
CFA — Как рассчитывать приведенную стоимость (PV) серии денежных потоков (аннуитета и перпетуитета)? | программа CFA
См. начало:
начало:
Многие аспекты управления инвестициями часто связаны с активами, которые предполагают серию (т.е. последовательность) денежных потоков, возникающих с течением времени.
Денежные потоки могут быть очень неравномерными, относительно одинаковыми или равными.
Также денежные потоки могут возникать в течение относительно коротких периодов времени, более длительных периодов времени или даже растягиваться на неопределенный срок.
Далее мы обсудим, как найти текущую или приведенную стоимость (PV) серии денежных потоков.
Расчет текущей стоимости (PV) серии равных денежных потоков.
Начнем с обычного или простого аннуитета (англ. ‘ordinary annuity’). Напомним, что обычный аннуитет означает равные аннуитетные платежи, причем 1-й платеж начинается через 1 период (т.е. в конце текущего периода / начале следующего / при t = 1).
Всего простой аннуитет включает N платежей с первым взносом при t = 1 и последним при t = N.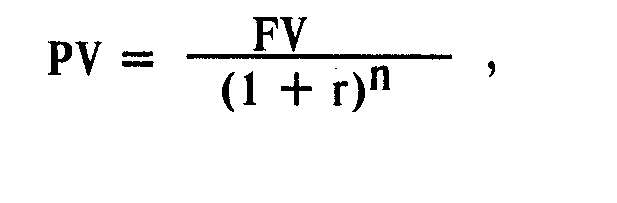 N} \over r \right]} \) (формула 11)
N} \over r \right]} \) (формула 11)
Точно так же, как и при вычислении будущей стоимости (FV) обычного аннуитета, мы находим текущую стоимость (PV), умножая сумму аннуитета на фактор текущей стоимости аннуитета (англ. ‘present value annuity factor’) — он заключен в квадратные скобки в формуле 11.
Пример расчета текущей (приведенной) стоимости обычного аннуитета.
Предположим, вы рассматриваете возможность покупки финансового актива, который обещает выплату в €1 000 каждый год в течение 5 лет с первым платежом через год.
Норма прибыли составляет 12% в год.
Сколько вы должны заплатить за этот актив?
Решение:
Чтобы узнать стоимость финансового актива, используйте формулу (11) текущей стоимости обычного аннуитета, со следующими данными:
A = €1,000
r = 12% = 0.12
N = 5
\( \mathbf { \begin{aligned} PV &= A \left[ 1-{1\over(1+r)^N} \over r \right] \\ &= €1 \ 000 \left[ 1-{1\over(1. 5} \over 0.12 \right] \end{aligned} } \)
5} \over 0.12 \right] \end{aligned} } \)
= €1,000 * (3.604776)
= €3,604.78
Серия денежных потоков в размере €1,000 в год в течение 5 лет на текущую дату составляет €3,604.78 при дисконтировании по ставке 12%.
Необходимость отслеживания фактических календарных сроков приводит нас к специфическому типу аннуитета: авансовому аннуитету или аннуитету пренумерандо (англ. ‘annuity due’).
При авансовом аннуитете 1-ый платеж выполняется в текущую дату (t = 0). В общей сложности авансовый аннуитет включает N платежей.
На рисунке ниже представлена временная шкала авансового аннуитета из 4-х платежей в размере $100.
Авансовый аннуитет в размере $100 за период.
На рисунке мы можем видеть авансовый аннуитет с 4-мя периодами, состоящий из двух частей:
- единовременная сумма в размере $100 на текущую дату (при t = 0) и
- обычный аннуитет в размере $100 за период в течение 3-х периодов.
 {-N} \over r \right] (1+r) } \)
{-N} \over r \right] (1+r) } \)Выражение стоимости будущих денежных потоков в сегодняшнем эквиваленте дает нам удобный способ сравнения аннуитетов. Следующий пример иллюстрирует этот подход.
Пример расчета авансового аннуитета как суммы текущей стоимости единичного денежного потока и обычного аннуитета.
Вы выходите на пенсию сегодня и должны либо получить свое пенсионное пособие в виде паушальной суммы (т.е. единовременной выплаты всех пенсионных накоплений), либо в виде аннуитета.
Сотрудник вашей компании, занимающийся выплатой пособий, предлагает вам две альтернативы:
- немедленную единовременную выплату в размере $2 млн. или
- аннуитет с 20 платежами в размере $200 000 в год с первым платежом от текущей даты.
Процентная ставка в вашем банке составляет 7% годовых с ежегодным начислением процентов.
Какой вариант обеспечивает большую текущую стоимость? (Игнорируйте любые налоговые различия между двумя вариантами.
 {19}} \over 0.07 \right] \end{aligned} } \)
{19}} \over 0.07 \right] \end{aligned} } \)
= $200,000(0.335595)
= $2,067,119.0519 платежей в размере $200 000 имеют текущую (приведенную) стоимость в размере $2,067,119.05. Добавив к этой сумме первоначальный платеж в размере $200,000, мы обнаружим, что общая стоимость аннуитета составляет $2,267,119.05.
Текущая стоимость аннуитета больше, чем единовременная альтернатива в размере $2 млн.
Теперь рассмотрим другой пример, подтверждающий эквивалентность текущей и будущей стоимости.
Пример расчета прогнозируемой текущей стоимости обычного аннуитета.
Менеджер немецкого пенсионного фонда ожидает, что пенсионерам будут выплачиваться пособия в размере €1 млн. в год. Пенсионные выплаты начнут осуществляться через 10 лет от текущей даты, при t = 10.
После того, как пособия начнут выплачиваться, эти выплаты продлятся до t = 39, что составляет в общей сложности 30 платежей.
Какова текущая (приведенная) стоимость пенсионного обязательства, если соответствующая годовая ставка дисконтирования для обязательств по пенсионному плану составляет 5% годовых, начисляемых ежегодно?
Решение:
Эта задача связана с аннуитетом, первый платеж по которому наступает через 10 лет, при t = 10.
 {30}} \over 0.05 \right] \end{aligned} } \)
{30}} \over 0.05 \right] \end{aligned} } \)
= €1,000,000 * (15.372451)
= €15,372,451.03Текущая стоимость обычного аннуитета с первым платежом в момент времени t = 10 (в млн. €).
На временной шкале мы отразили пенсионные выплаты в размере €1 млн., занимающие отрезок от t = 10 до t = 39.
Фигурная скобка и стрелка обозначают процесс нахождения текущей стоимости аннуитета, дисконтированной к моменту времени t = 9.
Текущая стоимость (PV) пенсионных пособий по состоянию на t = 9 составляет €15,372,451.03.
Далее задача заключается в том, чтобы найти текущую стоимость на текущую дату (при t = 0). Теперь мы можем полагаться на эквивалентность текущей стоимости и будущей стоимости (см. CFA — Эквивалентность приведенной и будущей стоимости денежных потоков).
Как показано на временной лини, мы можем рассматривать сумму при t = 9 в качестве будущей стоимости с точки зрения t = 0.
Мы вычислим текущую стоимость (PV) при t = 0 следующим образом:
FVN = €15,372,451.
 t \right] } \) (формула 12)
t \right] } \) (формула 12)Пока процентные ставки положительны, сумма факторов текущей стоимости позволяет получить формулу в следующем виде:
PV = A / r (формула 13)
Чтобы понять смысл этого преобразования, обратите внимание на формулу (11) текущей стоимости обычного аннуитета.
Поскольку N (количество периодов в аннуитете) переходит на бесконечность, выражение 1 / (1 + r)N приближается к 0, а формула 11 упрощается до формулы 13.
Эта формула потребуется, когда мы будем оценивать дивиденды от акций, поскольку акции не имеют предопределенного срока действия.
Акция, выплачивающая постоянные дивиденды, аналогична бессрочному аннуитету.
При первом платеже через год от текущей даты, перпетуитет в размере $10 в год при 20%-ой норме прибыли имеет текущую стоимость в размере $10 / 0,2 = $50 долларов.
Формула 13 справедлива только для бессрочного аннуитета с равными платежами.
 В примере выше первый платеж произошел при t = 1; поэтому мы вычисляем текущую стоимость при t = 0.
В примере выше первый платеж произошел при t = 1; поэтому мы вычисляем текущую стоимость при t = 0.Некоторые финансовые активы также соответствуют концепции бессрочного аннуитета. Определенные государственные облигации и привилегированные акции являются типичными примерами финансовых активов, которые обеспечивают равные выплаты в течение неопределенного срока.
Пример расчета текущей стоимости (PV) перпетуитета.
Британское правительство когда-то выпускало форму ценных бумаг, называемых «консолями» (англ. ‘consol bond’). Это — бессрочные облигации (англ. ‘perpetual bond’), которые обеспечивают равные денежные выплаты в течение неограниченного срока.
Если бессрочная облигация приносит £100 в год в течение неограниченного срока, сколько бы она стоила сегодня, если норма прибыли составляет 5%?
Решение:
Чтобы ответить на этот вопрос, мы можем использовать формулу 13 со следующими данными:
A = £100
r = 5% = 0. 05
05PV = A/r
= £100/0.05
= £2,000Облигация будет стоить £2 000.
Текущая стоимость на момент времени, отличный от текущей даты (t = 0).
На практике финансовым аналитикам часто приходится находить текущие значения стоимости, на различные моменты времени, отличные от t = 0.
Если мы рассчитаем перпетуитет, начинающийся с платежа в размере $100 на 2-й год, то мы получим PV1 = $ 100 / 0,05 = $2 000 при 5%-й ставке. Кроме того, мы можем рассчитать PV на текущую дату как PV0 = $2,000 / 1.05 = $ 1,904.76.
Рассмотрим аналогичную ситуацию, в которой денежные потоки в размере $6 в год начинаются в конце 4-го года и продолжаются в конце каждого года после этого с последним потоком денежных средств в конце 10-го года.
По состоянию на конец 3-го года мы сталкиваемся с типичным 7-летним обычным аннуитетом. Мы можем найти текущую стоимость аннуитета на конец 3-го года, а затем привести эту стоимость к текущей дате.

При процентной ставке 5% денежные потоки в размере $6 в год, начинающиеся в конце 4-го года, будут стоить $34,72 на конец 3-го года (t = 3) и $29,99 на текущую дату (t = 0).
Следующий пример иллюстрирует важную концепцию, согласно которой начинающийся в будущем аннуитет или перпетуитет может быть выражен в текущей стоимости за один период до первого платежа. Эта стоимость может быть приведена к текущей стоимости на сегодняшнюю дату.
Пример расчета текущей стоимости (PV) бессрочного аннуитета (перпетуитета) с отсроченной первой выплатой.
Рассмотрим перпетуитет с равными платежами в £100 в год, с первой выплатой, начинающейся при t = 5.
Какова будет его текущая стоимость на сегодняшнюю дату (при t = 0), при 5-процентной ставке дисконтирования?
Решение:
Во-первых, мы находим текущую стоимость перпетуитета при t = 4, а затем дисконтируем эту сумму к текущей дате t = 0. (Напомним, что у перпетуитета и обычного аннуитета первый платеж осуществляется на конец первого периода, что объясняет индекс t = 4 для нашего расчета текущей стоимости).

1. Находим текущую стоимость перпетуитета при t = 4:
A = £100
r = 5% = 0.05PV = A/r
= £100/0.05
= £2,0002. Находим текущую стоимость будущего значения при
t = 4.С точки зрения сегодняшней даты t = 0 текущую стоимость в £2,000 можно считать будущей стоимостью.
Теперь нам нужно найти текущую стоимость £2,000 при
t = 0:FVN = £2,000 (текущая стоимость при t = 4)
r = 5% = 0.05
N = 4PV = FVN * (1 + r)—N
= £2,000 * (1.05)-4
= £2,000 * (0.822702)
= £1,645.40Приведенная стоимость перпетуитета на текущую дату составляет £1,645.40.
Как обсуждалось ранее, аннуитет представляет собой серию платежей с фиксированной (одинаковой) суммой в течение определенного количества периодов.

В ситуации с перпетуитетом число периодов бесконечно. В этом случае мы предоставляем бессрочное обязательство производить платежи, и эти платежи имеют одинаковую сумму. Тем не менее, первая (1) часть перпетуитета отсрочена и выплачивается при t = 5; после этого платежи продолжаются бесконечно.
Выплаты по второй (2) части перпетуитета компенсируют смещение 1-го платежа первой (1) части перпетуитета к t = 5.
Благодаря этому перпетуитет с отсроченной 1-й выплатой (до t = 5) обеспечивает выплаты при t = 1, 2, 3 и 4. Выплаты за эти 4 периода точно соответствуют определению обычного аннуитета с четырьмя платежами.
Таким образом, мы можем представить обычный аннуитет как разницу между двумя перпетуитетами с равными платежами, но с разными датами начала выплат.
Следующий пример иллюстрирует этот результат.
Пример расчета текущей стоимости обычного аннуитета как разницы между текущей стоимостью (PV) и прогнозируемым (отсроченным) перпетуитетом.
С учетом 5%-ой ставки дисконтирования, найдите текущую (приведенную) стоимость 4-летнего обычного аннуитета в размере £100 в год, с выплатами начиная с 1-го года, в качестве разницы между следующими двумя перпетуитетами:
- Перпетуитет 1 на £100 в год, начиная с 1-го года (первый платеж при t = 1).

- Перпетуитет 2 на £100 в год, начиная с 5-го года (первый платеж при t = 5).
Решение:
Если мы вычтем Перпетуитет 2 из Перпетуитета 1, мы получим обычный аннуитет в размере £100 за 4 года (платежи при t = 1, 2, 3, 4).
Вычитая текущую стоимость Перпетуитета 2 из Перпетуитета 1, мы придем к текущей (приведенной) стоимости четырехлетнего обычного аннуитета:
PV0 (Перпетуитет 1) = £100 / 0.05 = £2,000
PV4 (Перпетуитет 2) = £100 / 0.05 = £2,000
PV0 (Перпетуитет 2) = £2,000 / (1.05)4 = £1,645.40PV0 (Аннуитет)
= PV0 (Перпетуитет 1) — PV0 (Перпетуитет 2)
= £2,000 — £1,645.40
= £354.60Текущая стоимость 4-летнего обычного аннуитета равна £2,000 — £1,645.40 = £354.60.
Как вычислять текущую стоимость (PV) для серии неравных денежных потоков?
Когда мы имеем неравные денежные потоки, мы должны сначала найти текущую стоимость (PV) каждого отдельного денежного потока, а затем суммировать соответствующие значения PV.

Для серии (последовательности) с большим количеством денежных потоков мы обычно используем электронную таблицу.
В таблице ниже приведена последовательность денежных потоков с
- временными периодами в 1-м столбце,
- денежными потоками во 2-м столбце и
- текущей стоимостью (PV) каждого денежного потока в 3-м столбце.
В итоговой строке таблице показана сумма приведенных значений для всей серии денежных потоков.
Серия неравных денежных потоков и их приведенная стоимость при ставке 5%. Период
Денежный поток ($)
PV при t=0
1
1,000
$1,000(1.05)-1 =
$952.
 38
382
2,000
$2,000(1.05)-2 =
$1,814.06
3
4,000
$4,000(1.05)-3 =
$3,455.35
4
5,000
$5,000(1.05)-4 =
$4,113.51
5
6,000
$6,000(1.05)-5 =
$4,701.16
Сумма =
$15,036.
 46
46Мы могли бы рассчитать будущую стоимость (FV) серии этих денежных потоков, вычислив ее по отдельности для каждого потока с использованием формулы расчета будущей стоимости.
Однако мы уже знаем текущую стоимость этой серии, поэтому мы можем легко применить принцип временной эквивалентности для всей суммы денежных потоков сразу.
Будущая стоимость серии денежных потоков составляет $19,190.76 и эквивалентна единовременному денежному потоку размере $15,036.46, с приведением к периоду t = 5:
PV = $15,036.46
N = 5
r = 5% = 0.05FVN = PV * (1 + r)N
= $15,036.46 * (1.05)5
= $15,036.46 * (1.276282)
= $19,190.76См. далее:
Функция ПС (PV) — Справочник
Обязательный. Процентная ставка за период.
Например, если получен кредит на автомобиль под 10 процентов годовых и выплаты производятся ежемесячно, процентная ставка за месяц составит 10%/12 (0,83%). В качестве значения аргумента «ставка» нужно ввести в формулу 10%/12, 0,83% или 0,0083.
В качестве значения аргумента «ставка» нужно ввести в формулу 10%/12, 0,83% или 0,0083.Обязательный. Общее число периодов платежей для ежегодного платежа.
Например, если получен кредит на 4 года на покупку автомобиля и платежи производятся ежемесячно, то кредит имеет 4*12 (или 48) периодов. В качестве значения аргумента «кпер» в формулу нужно ввести число 48.Обязательный. Выплата, производимая в каждый период и не меняющаяся на протяжении всего периода ежегодного платежа. Обычно аргумент «плт» состоит из выплат в счет основной суммы и платежей по процентам, но не включает в себя другие сборы или налоги.
Например, ежемесячная выплата по кредиту в размере 10 000 р. под 12 процентов годовых на 4 года составит 263,33р. В качестве значения аргумента «плт» нужно ввести в формулу число -263,33. Если он опущен, аргумент «бс» является обязательным.Необязательный. Значение будущей стоимости, т. е. желаемого остатка средств после последнего платежа.
Необязательный. Число 0 или 1, обозначающее, когда должна производиться выплата. Если аргумент «бс» опущен, предполагается, что он равен 0 (например, будущая стоимость для займа равна 0).
Если аргумент «бс» опущен, предполагается, что он равен 0 (например, будущая стоимость для займа равна 0).
Предположим, что для определенной цели требуется накопить 50 000 р. за 18 лет: в этом случае будущая стоимость равна 50 000 р. Предположив, что заданная процентная ставка останется без изменений, можно определить, какую сумму необходимо откладывать каждый месяц. Если аргумент «бс» опущен, необходимо использовать аргумент «плт».Тип Когда нужно платить 0 или опущен В конце периода 1 В начале периода Текущая стоимость – PV – Финансовая энциклопедия
Что такое Текущая стоимость – PV?
Приведенная стоимость (PV) – это текущая стоимость будущей денежной суммы или потока денежных средств при заданной норме прибыли . Будущие денежные потоки дисконтируются по ставке дисконтирования, и чем выше ставка дисконтирования , тем ниже приведенная стоимость будущих денежных потоков.
 Определение подходящей ставки дисконтирования является ключом к правильной оценке будущих денежных потоков, будь то прибыль или долговые обязательства.
Определение подходящей ставки дисконтирования является ключом к правильной оценке будущих денежных потоков, будь то прибыль или долговые обязательства.Ключевые моменты
- Приведенная стоимость означает, что сумма денег сегодня стоит больше, чем такая же сумма в будущем.
- Другими словами, приведенная стоимость показывает, что деньги, полученные в будущем, не стоят столько, сколько эквивалентная сумма, полученная сегодня.
- Неизрасходованные сегодня деньги могут потерять ценность в будущем из-за предполагаемой годовой ставки из-за инфляции или нормы прибыли, если деньги были вложены.
- Расчет приведенной стоимости предполагает предположение, что доходность средств может быть получена за период.
Понимание приведенной стоимости (PV)
Приведенная стоимость – это концепция, согласно которой сумма денег сегодня будет стоить больше, чем та же сумма в будущем. Другими словами, деньги, полученные в будущем, не стоят столько, сколько эквивалентная сумма, полученная сегодня.

Получение 1000 долларов сегодня будет стоить более 1000 долларов через пять лет. Почему? Инвестор может вложить 1000 долларов сегодня и, предположительно, получить доход в течение следующих пяти лет. Приведенная стоимость учитывает любую процентную ставку, которую может принести инвестиция.
Например, если инвестор получает 1000 долларов сегодня и может получать доходность 5% в год, то 1000 долларов сегодня определенно дороже, чем получение 1000 долларов через пять лет. Если инвестор ждал пять лет, чтобы получить 1000 долларов, возникли бы альтернативные издержки или инвестор потерял бы доходность за пять лет.
Инфляция и покупательная способность
Инфляция – это процесс, при котором цены на товары и услуги со временем растут. Если вы получите деньги сегодня, то сможете покупать товары по сегодняшним ценам. Предположительно, инфляция вызовет рост цен на товары в будущем, что снизит покупательную способность ваших денег.
Можно ожидать, что деньги, не потраченные сегодня, потеряют ценность в будущем из-за некоторой подразумеваемой годовой ставки, которой может быть инфляция или норма прибыли, если деньги были вложены.
 Формула приведенной стоимости дисконтирует будущую стоимость к сегодняшним долларам, принимая во внимание предполагаемую годовую ставку либо из инфляции, либо из нормы прибыли, которая могла бы быть достигнута, если бы сумма была инвестирована.
Формула приведенной стоимости дисконтирует будущую стоимость к сегодняшним долларам, принимая во внимание предполагаемую годовую ставку либо из инфляции, либо из нормы прибыли, которая могла бы быть достигнута, если бы сумма была инвестирована.Ставка дисконтирования для определения приведенной стоимости
Ставка дисконтирования – это норма доходности инвестиций, которая применяется для расчета приведенной стоимости. Другими словами, ставка дисконтирования была бы упущенной нормой прибыли, если бы инвестор решил принять сумму в будущем по сравнению с той же суммой сегодня. Ставка дисконтирования, выбранная для расчета приведенной стоимости, очень субъективна, потому что это ожидаемая норма прибыли, которую вы получили бы, если бы вы вложили сегодняшние доллары в течение определенного периода времени.
Во многих случаях определяется безрисковая норма прибыли, которая используется в качестве ставки дисконтирования, которую часто называют пороговой ставкой . Ставка представляет собой норму прибыли, которую необходимо получить от инвестиций или проекта, чтобы их можно было продолжать.
 доходности , инвестиции должны приносить как минимум более 2%, чтобы оправдать риск.
доходности , инвестиции должны приносить как минимум более 2%, чтобы оправдать риск.Ставка дисконтирования – это сумма временной стоимости и соответствующей процентной ставки, которая математически увеличивает будущую стоимость в номинальном или абсолютном выражении. И наоборот, ставка дисконтирования используется для расчета будущей стоимости с точки зрения приведенной стоимости, позволяя кредитору рассчитаться по справедливой сумме любых будущих доходов или обязательств по отношению к приведенной стоимости капитала. Слово «скидка» относится к будущей стоимости, дисконтируемой до текущей стоимости.
Расчет дисконтированной или приведенной стоимости чрезвычайно важен во многих финансовых расчетах. Например, чистая приведенная стоимость , доходность облигаций и пенсионные обязательства зависят от дисконтированной или приведенной стоимости. Изучение того, как использовать финансовый калькулятор для расчета приведенной стоимости, может помочь вам решить, следует ли вам принимать такие предложения, как скидка наличными, финансирование 0% при покупке автомобиля или выплаты баллов по ипотеке.
 n} \\ & \ textbf {где:} \\ & \ text {FV} = \ text {Будущее значение} \\ & r = \ text {Норма прибыли} \\ & n = \ text {Количество периодов} \\ \ end {выровнено}Взаимодействие с другими людьмиТекущее значениезнак равно(1+г)п
n} \\ & \ textbf {где:} \\ & \ text {FV} = \ text {Будущее значение} \\ & r = \ text {Норма прибыли} \\ & n = \ text {Количество периодов} \\ \ end {выровнено}Взаимодействие с другими людьмиТекущее значениезнак равно(1+г)п- Введите сумму, которую вы ожидаете получить в будущем, в числитель формулы.
- Определите процентную ставку, которую вы ожидаете получить в период между настоящим моментом и будущим, и укажите ставку в виде десятичной дроби вместо «r» в знаменателе.
- Введите период времени как показатель степени «n» в знаменателе. Итак, если вы хотите рассчитать приведенную стоимость суммы, которую ожидаете получить через три года, вы должны подставить цифру три вместо «n» в знаменателе.
- Существует ряд онлайн-калькуляторов, в том числе и этот калькулятор приведенной стоимости .
Будущая стоимость против текущей стоимости
Сравнение текущей стоимости с будущей стоимостью (FV) лучше всего иллюстрирует принцип временной стоимости денег и необходимость взимания или выплаты дополнительных процентных ставок, основанных на риске.
 Проще говоря, с течением времени деньги сегодня стоят больше, чем те же деньги завтра. Будущая стоимость может относиться к будущим денежным поступлениям от инвестирования сегодняшних денег или будущим платежам, необходимым для возврата денег, взятых сегодня в долг.
Проще говоря, с течением времени деньги сегодня стоят больше, чем те же деньги завтра. Будущая стоимость может относиться к будущим денежным поступлениям от инвестирования сегодняшних денег или будущим платежам, необходимым для возврата денег, взятых сегодня в долг.Будущая стоимость (FV) – это стоимость текущего актива на определенную дату в будущем, основанную на предполагаемой скорости роста. Уравнение FV предполагает постоянные темпы роста и единовременный авансовый платеж, который остается нетронутым в течение всего периода инвестирования. Расчет FV позволяет инвесторам с разной степенью точности прогнозировать сумму прибыли, которую можно получить от различных инвестиций.
Приведенная стоимость (PV) – это текущая стоимость будущей суммы денег или потока денежных средств при заданной норме прибыли. Приведенная стоимость принимает будущую стоимость и применяет ставку дисконтирования или процентную ставку, которая может быть получена в случае инвестирования. Будущая стоимость говорит вам, сколько стоит инвестиция в будущем, а текущая стоимость говорит вам, сколько вам нужно в сегодняшних долларах, чтобы заработать определенную сумму в будущем.

Критика текущей стоимости
Как указывалось ранее, расчет приведенной стоимости включает допущение о том, что доходность средств может быть получена за определенный период времени. В приведенном выше обсуждении мы рассмотрели одну инвестицию в течение одного года. Однако, если компания решает продолжить серию проектов, которые имеют разную норму прибыли для каждого года и каждого проекта, приведенная стоимость становится менее определенной, если эти ожидаемые нормы прибыли нереалистичны. Важно учитывать, что при принятии любого инвестиционного решения не гарантируется процентная ставка, а инфляция может снизить доходность инвестиций.
Пример приведенной стоимости
Допустим, у вас есть выбор: вам заплатят 2000 долларов сегодня или 2200 долларов через год. У вас также есть возможность инвестировать 2000 долларов, которые принесут 3% прибыли в течение следующего года. Какой вариант лучше?
- Используя формулу приведенной стоимости, расчет составит 2200 долларов (FV) / (1 +.
 1.
1. - PV = 2135,92 доллара США, или минимальная сумма, которую вам нужно будет заплатить сегодня, чтобы иметь 2200 долларов через год. Другими словами, если бы вам заплатили 2000 долларов сегодня и исходя из процентной ставки 3%, этой суммы было бы недостаточно, чтобы дать вам 2200 долларов через год.
Конечно, расчет приведенной стоимости включает предположение, что вы можете заработать 3% от 2000 долларов в течение следующего года. Если бы процентная ставка была намного выше, было бы разумнее взять 2 000 долларов сегодня и инвестировать средства, потому что через год это принесет большую сумму, чем 2200 долларов.
Приведенная стоимость обеспечивает основу для оценки справедливости любых будущих финансовых выгод или обязательств. Например, будущий возврат денежных средств, дисконтированный до приведенной стоимости, может стоить или не стоить потенциально более высокой покупной цены. Тот же финансовый расчет применяется для 0% финансирования при покупке автомобиля.

Выплата некоторого процента по более низкой цене стикера может сработать для покупателя лучше, чем уплата нулевого процента по более высокой цене стикера. Выплата ипотечных баллов сейчас в обмен на более низкие выплаты по ипотеке в дальнейшем имеет смысл только в том случае, если приведенная стоимость будущих сбережений по ипотеке больше, чем выплаченные сегодня ипотечные баллы.
Часто задаваемые вопросы
Как вы рассчитываете приведенную стоимость?
Приведенная стоимость рассчитывается путем дисконтирования будущих денежных потоков, ожидаемых от инвестиции, до настоящего времени. Для этого инвестору нужны три ключевых точки данных: ожидаемые денежные потоки, количество лет, в течение которых денежные потоки будут выплачиваться, и их ставка дисконтирования. Ставка дисконтирования является очень важным фактором, влияющим на приведенную стоимость, при этом более высокие ставки дисконтирования приводят к более низкой приведенной стоимости, и наоборот. Используя эти переменные, инвесторы могут рассчитать приведенную стоимость по формуле:
PREсекйнт Vвл¯uезнак равноFV(1+р)пжчере:FVзнак равноРутурх Vлуйрзнак равноРтеоеретутп пзнак равноNumber of periods\ begin {align} & \ text {Present Value} = \ dfrac {\ text {FV}} {(1 + r) ^ n} \\ & \ textbf {где:} \\ & \ text {FV} = \ text {Будущее значение} \\ & r = \ text {Норма прибыли} \\ & n = \ text {Количество периодов} \\ \ end {выровнено}Взаимодействие с другими людьмиТекущее значениезнак равно(1+г)п
Какие примеры приведенной стоимости?
В качестве иллюстрации рассмотрим сценарий, в котором инвестиция генерирует денежные потоки в размере 500 долларов США в год в течение 5 лет, а наша ставка дисконтирования составляет 6,00%.
 Применяя нашу формулу приведенной стоимости, мы получим приведенную стоимость в 2106,18 долларов. Другими словами, если бы кто-то спросил нас, сколько стоит эта инвестиция, мы бы ответили, что она стоит не более 2106,18 долларов. С другой стороны, если бы наша ставка дисконтирования составляла 12,00%, то ее приведенная стоимость была бы намного ниже, что сделало бы цену в 2 106,18 доллара слишком высокой.
Применяя нашу формулу приведенной стоимости, мы получим приведенную стоимость в 2106,18 долларов. Другими словами, если бы кто-то спросил нас, сколько стоит эта инвестиция, мы бы ответили, что она стоит не более 2106,18 долларов. С другой стороны, если бы наша ставка дисконтирования составляла 12,00%, то ее приведенная стоимость была бы намного ниже, что сделало бы цену в 2 106,18 доллара слишком высокой.Почему важна текущая стоимость?
Приведенная стоимость важна, потому что она позволяет инвесторам судить о том, является ли цена, которую они платят за инвестиции, уместной. Например, в нашем предыдущем примере ставка дисконтирования 12% снизила бы приведенную стоимость инвестиций только до 1802,39 доллара. В этом сценарии мы очень неохотно будем платить за инвестиции больше этой суммы, поскольку наш расчет приведенной стоимости показывает, что мы могли бы найти лучшие возможности в другом месте. Подобные расчеты приведенной стоимости играют решающую роль в таких областях, как инвестиционный анализ, управление рисками и финансовое планирование.
#Т
Метод расчета чистой текущей стоимости (чистого приведенного эффекта) (net present value — NPV)
Показатель чистой текущей стоимости является производным от показателя текущей стоимости. Под текущей стоимостью (present value — PV) понимается стоимость будущих поступлений денежных средств (future value — FV), отнесенная к настоящему моменту с помощью процедуры дисконтирования. Показатель PV можно рассчитать по формуле, описывающей простую финансовую операцию: размещение денежных средств на условиях срочности, платности, возвратности с единовременным погашением:
PV + r • PV = FV,
где PV — сумма денежных средств, предназначенных для размещения на условиях срочности, платности, возвратности;
r — процентная ставка, являющаяся платой за предоставленные в кредит денежные средства;
FV — сумма погашения кредита, включающая первоначальную сумму долга и проценты.
Преобразование вышеприведенной формулы простой финансовой операции позволит получить формулу расчета показателя текущей стоимости:
PV + r • PV = FV;
PV (1 + r) = FV;
PV= FV / 1+ r = FV 1 / 1 + r;
PV = FV 1 / 1+r.

Если погашение кредита с процентами происходит частями в течение нескольких лет (или частями в течение нескольких лет
поступают доходы от проекта), то формула расчета текущей стоимости будет иметь следующий вид:
Под чистой текущей стоимостью (net present value — NPV) понимается разница между общей суммой дисконтированных потоков будущих поступлений денежных средств, генерируемых данным проектом, и общей суммой инвестиций (invest cost — IС).
где ? FVn — общая сумма будущих поступлений от проекта;
r — доходность проекта;
IС — сумма инвестиций.
Показатель чистой текущей стоимости (NPV) представляет собой разность между совокупными доходами от проекта и совокупными расходами, связанными с проектом. Разность может быть больше нуля, равна нулю или меньше нуля.
Если:
NPV > 0, то проект следует принять;
NPV = 0, то проект является ни прибыльным, ни убыточным;
NPV < 0, то проект следует отвергнуть.

FV и Формула PV в Excel
Я пытаюсь рассчитать пожизненную ценность клиента. Предположим, новый клиент платит $100K в год и остается на 5 лет. Давайте дисконтируем любые платежи будущих лет по ставке 10%.
Это ручной расчет:
Year 1 $100,000.00 Year 2 $90,000.00 Year 3 $81,000.00 Year 4 $72,900.00 Year 5 $65,610.00 --------------------- Total $409,510.00Я могу получить то же самое значение, используя FV с отрицательной ставкой.
FV(-0.1,5,-100000,0,0) = $409,510.00То, что я пытаюсь сделать, — это получить то же самое значение, используя PV. И это не совсем то же самое:
PV(0.1,5,-100000,0,1) = $416,986.54Я не совсем понимаю, чего мне здесь не хватает. Понимает ли MS Office Excel 2010 PV дисконтирование по-другому?
excel finance
Поделиться Источник Serguei 12 февраля 2016 в 15:042 ответа
- Excel Формула Оплаты
Может ли кто-нибудь объяснить мне формулу PMT в excel? =-PMT ( 1) ставка 2) nper 3) pv 4) [FV] 5) [Тип] ) Выше приведено приблизительное представление о том, что такое формула ПМТ.
 Periods
Periods Причина разницы в вычислениях заключается в математической разнице между двумя элементами — для фона см. Здесь: http://www.investopedia.com/пошаговое руководство/корпоративное-finance/3/time-value-money/future-value.aspx и здесь: http://www.investopedia.com/пошаговое руководство/корпоративное-finance/3/time-value-money/present-value-discounting.aspx .
Короче говоря, если у вас сегодня есть $100k и вы инвестируете их в то, что дает вам 10% каждый год, то каждый год вы добавляете 10% текущего баланса, чтобы получить новый баланс. т. е.: в год 1 вы добавляете 100k * 10% = 10k, давая новую общую сумму 110k; в год 2 вы добавляете 110k * 10% = 11k, давая новую общую сумму 121k и т. Д. — Математически сумма каждого года определяется по формуле, приведенной выше для расчета FV.
Где это становится сложным, так это то, что вы даете себе отрицательную процентную ставку — то есть каждый год значение уменьшается каждый год на 10%. Вы пытались использовать расчет FV с отрицательной процентной ставкой, но это не совсем правильно.
 То, что вы должны использовать, — это формула PV.
То, что вы должны использовать, — это формула PV.Для формулы PV, если вы знаете, что будете получать 100 тысяч долларов каждый год, вам нужно определить, сколько наличных денег вам понадобилось бы изначально, чтобы заработать такую же сумму — это текущая стоимость потока денежных потоков. Теперь вам нужно ‘gross-up’ значение потока доходов каждого года. Формула для этого брутто-апа выведена математически и приводит к тому, что у меня есть выше для PV. Подумайте об этом так: если есть рубашка, которая обычно стоит $100, а сейчас 30%, вы можете увидеть, что вы просто умножаете ее на 30%,, чтобы получить $70., Но если вы видите рубашку в продаже за $70,, и она 30%, то для определения первоначальной базовой цены вам нужно взять $70 &, разделить на .3, что дает нам $100.
Чтобы доказать себе, что формула PV подходит, возьмите поток дохода, скажем, за 4 год [3 периода процентов позже, предполагая, что первый платеж будет получен в день 0]: 100k / (1 + 10%)^3 = $75,131.
 3 = 100 тысяч.
3 = 100 тысяч.Это важное финансовое различие, и вы должны прочитать источники, на которые я ссылался, чтобы убедиться, что вы его понимаете.
Поделиться Grade ‘Eh’ Bacon 12 февраля 2016 в 15:30
2Есть разница в расчетах. FV берет 100 000 и дисконтирует его на 10% до числа X, так что X составляет 90% от исходного значения (т. е. X=90 000). PV, напротив, дисконтирует его до числа X, так что 100 000 будет 10% больше, чем X. Быстрая математика говорит, что X будет be 10/11 из 100 000, т. е. 90909.09.
Действительно, если мы применим этот расчет 5 раз:
Year 1 $100,000.00 Year 2 $90,909.09 Year 3 $82,644.63 Year 4 $75,131.48 Year 5 $68,301.35 --------------------- Total $416,986.5Я не знаю, есть ли способ заставить их вести себя одинаково (я не думаю, что есть, так как они вычисляют разные вещи), но поскольку FV решает вашу проблему, почему бы просто не использовать это?
Поделиться ShakesBeer 12 февраля 2016 в 15:20
Похожие вопросы:
как рассчитать excel pmt с помощью phpЯ пытался реализовать функцию pmt, используемую в excel, в php.
 У меня есть формула, но расчеты показывают неверные. Его процентная ставка 6% на период 30 лет, конечное значение — 833333. Правильный…
У меня есть формула, но расчеты показывают неверные. Его процентная ставка 6% на период 30 лет, конечное значение — 833333. Правильный…
Как вычислить PV и Формулу FV в JS?Я хочу вычислить PV и FV в JavaScript, на самом деле до этого я работал в excel, у которого была функция PV и FV, так что эти функции действительно помогли мне, и теперь я ищу что-то подобное в…
Точность функции ‘FV’ в ExcelВот такой сценарий: Инвестирование 10 фунтов стерлингов в месяц в течение 12 месяцев (инвестирование в начале месяца). Годовая эквивалентная норма прибыли 5%. ежемесячно = 5%/12= 0.4166667% Теперь с…
Excel Формула ОплатыМожет ли кто-нибудь объяснить мне формулу PMT в excel? =-PMT ( 1) ставка 2) nper 3) pv 4) [FV] 5) [Тип] ) Выше приведено приблизительное представление о том, что такое формула ПМТ. Но я не уверен в…
Как я могу воспроизвести функцию Excel FV в PHP?Я преобразую некоторые довольно сложные вычисления из таблицы Excel в PHP.
 Я застрял на преобразовании функции Excel FV, которая определяется таким образом: FV( interest_rate, number_payments,…
Я застрял на преобразовании функции Excel FV, которая определяется таким образом: FV( interest_rate, number_payments,…
Разрыв в результатах функции приведенной стоимости Excel PVФункция PV от Excel (приведенная стоимость инвестиций), кажется, делает внезапный скачок где-то и вызывает ошибку. Например: WorksheetFunction.PV(-19, 240, 500000) вернет значение в то время как:…
Нужна помощь в преобразовании формулы PV в PHPМне нужна помощь в преобразовании следующего excel formula в PHP PV(.0588/12,300,868.0583333) Результат, который я ожидаю, — 136,275.88 , но результат, который я получаю, — 590573.166 . Я потратил…
Как преобразовать функцию excel PV в phpЯ пытаюсь преобразовать некоторые функции PV из Microsoft Excel в PHP: PV( rate, nper, pmt, FV, Type ) Это заняло у меня много времени. По сути, мне нужно воспроизвести эту функциональность в…
решение для сложных процентов между PV и «summation» FV?Данные входы: present value = 11, SUMMATIONS of future values that = 126, and n = 7 (periods of change) как я могу решить для скорости цепочки, которая создала бы цепочку, суммирующуюся в FV? Это.
 ..
..
Формула приведенной стоимости с использованием FV и платежейВ Excel, если я введу =PV(8%/12,12,-1970,0,0) , я получу $22,647 Формула для этого такова: select @PAYMENT * (Power((1 + @RATE / 100),@NPER) -1) / (((@RATE / 100)) * Power((1 + @RATE / 100),@NPER))…
Текущая стоимость — определение PV
Что такое приведенная стоимость (PV)?
Приведенная стоимость (PV) — это текущая стоимость будущей суммы денег или потока денежных средств при заданной норме прибыли. Будущие денежные потоки дисконтируются по ставке дисконтирования, и чем выше ставка дисконтирования, тем ниже приведенная стоимость будущих денежных потоков. Определение подходящей ставки дисконтирования является ключом к правильной оценке будущих денежных потоков, будь то прибыль или долговые обязательства.
Ключевые выводы
- Приведенная стоимость означает, что сумма денег сегодня стоит больше, чем такая же сумма в будущем.

- Другими словами, приведенная стоимость показывает, что деньги, полученные в будущем, не стоят столько, сколько эквивалентная сумма, полученная сегодня.
- Неизрасходованные сегодня деньги могут потерять ценность в будущем из-за предполагаемой годовой ставки из-за инфляции или нормы прибыли, если деньги были вложены.
- Расчет приведенной стоимости предполагает допущение, что доходность средств может быть получена за период.
Общие сведения о приведенной стоимости (PV)
Приведенная стоимость — это концепция, согласно которой сумма денег сегодня будет стоить больше, чем та же сумма в будущем. Другими словами, деньги, полученные в будущем, не стоят столько, сколько эквивалентная сумма, полученная сегодня.
Получение 1000 долларов сегодня будет стоить более 1000 долларов через пять лет. Почему? Инвестор может вложить 1000 долларов сегодня и предположительно получить доход в течение следующих пяти лет. Приведенная стоимость учитывает любую процентную ставку, которую может принести инвестиция.

Например, если инвестор получает 1000 долларов сегодня и может получать доходность 5% в год, то сегодняшняя 1000 долларов, безусловно, стоит больше, чем получение 1000 долларов через пять лет. Если инвестор будет ждать 1000 долларов в течение пяти лет, возникнут альтернативные издержки или инвестор потеряет доходность за пять лет.
Инфляция и покупательная способность
Инфляция — это процесс, при котором цены на товары и услуги со временем растут. Если вы получите деньги сегодня, вы сможете покупать товары по сегодняшним ценам.Предположительно, инфляция вызовет рост цен на товары в будущем, что снизит покупательную способность ваших денег.
Можно ожидать, что деньги, не потраченные сегодня, потеряют ценность в будущем из-за некоторой подразумеваемой годовой ставки, которой может быть инфляция или норма прибыли, если деньги были вложены. Формула приведенной стоимости дисконтирует будущую стоимость к сегодняшним долларам с учетом предполагаемой годовой ставки либо из инфляции, либо из нормы прибыли, которая могла бы быть получена, если бы сумма была инвестирована.

Ставка дисконтирования для определения приведенной стоимости
Ставка дисконтирования — это норма доходности инвестиций, которая применяется при расчете приведенной стоимости. Другими словами, ставка дисконтирования была бы упущенной нормой прибыли, если бы инвестор решил принять сумму в будущем по сравнению с той же суммой сегодня. Ставка дисконтирования, выбранная для расчета приведенной стоимости, очень субъективна, потому что это ожидаемая норма прибыли, которую вы получили бы, если бы вы вложили сегодняшние доллары в течение определенного периода времени.
Во многих случаях определяется безрисковая норма прибыли, которая используется в качестве ставки дисконтирования, которую часто называют пороговой ставкой. Ставка представляет собой норму прибыли, которую необходимо получить от инвестиций или проекта, чтобы их можно было продолжать. Ставка казначейских облигаций США часто используется в качестве безрисковой ставки, поскольку казначейские облигации поддерживаются правительством США.
 Так, например, если двухлетнее казначейство выплачивает 2% годовых или доходность, инвестиции должны приносить как минимум более 2%, чтобы оправдать риск.
Так, например, если двухлетнее казначейство выплачивает 2% годовых или доходность, инвестиции должны приносить как минимум более 2%, чтобы оправдать риск.Ставка дисконтирования — это сумма временной стоимости и соответствующей процентной ставки, которая математически увеличивает будущую стоимость в номинальном или абсолютном выражении. И наоборот, ставка дисконтирования используется для расчета будущей стоимости с точки зрения приведенной стоимости, позволяя кредитору рассчитаться по справедливой сумме любых будущих доходов или обязательств по отношению к приведенной стоимости капитала. Слово «скидка» относится к будущей стоимости, дисконтируемой до текущей стоимости.
Расчет дисконтированной или приведенной стоимости чрезвычайно важен во многих финансовых расчетах.Например, чистая приведенная стоимость, доходность облигаций и пенсионные обязательства зависят от дисконтированной или приведенной стоимости. Изучение того, как использовать финансовый калькулятор для расчета приведенной стоимости, может помочь вам решить, следует ли вам принимать такие предложения, как скидка наличными, финансирование 0% при покупке автомобиля или выплаты баллов по ипотеке.
 n} \\ & \ textbf {где:} \\ & \ text {FV} = \ text {Будущее значение} \\ & r = \ text {Норма прибыли} \\ & n = \ text {Количество периодов} \\ \ end {выровнено}
Текущая стоимость = (1 + r) nFV, где: FV = будущий оценщик = норма прибыли n = количество периодов
n} \\ & \ textbf {где:} \\ & \ text {FV} = \ text {Будущее значение} \\ & r = \ text {Норма прибыли} \\ & n = \ text {Количество периодов} \\ \ end {выровнено}
Текущая стоимость = (1 + r) nFV, где: FV = будущий оценщик = норма прибыли n = количество периодов- Введите будущую сумму, которую вы ожидаете получить, в числитель формулы.
- Определите процентную ставку, которую вы ожидаете получить в период между настоящим моментом и будущим, и укажите ставку в виде десятичной дроби вместо буквы «r» в знаменателе.
- Введите период времени как показатель степени «n» в знаменателе. Итак, если вы хотите рассчитать приведенную стоимость суммы, которую ожидаете получить через три года, вы должны подставить цифру три вместо «n» в знаменателе.
- Существует ряд онлайн-калькуляторов, в том числе калькулятор текущей стоимости.
Будущая стоимость vs.Текущая стоимость
Сравнение текущей стоимости с будущей стоимостью (FV) лучше всего иллюстрирует принцип временной стоимости денег и необходимость взимания или выплаты дополнительных процентных ставок, основанных на риске.
 Проще говоря, с течением времени деньги сегодня стоят больше, чем те же деньги завтра. Будущая стоимость может относиться к будущим денежным потокам от инвестирования сегодняшних денег или будущим платежам, необходимым для возврата денег, взятых сегодня в долг.
Проще говоря, с течением времени деньги сегодня стоят больше, чем те же деньги завтра. Будущая стоимость может относиться к будущим денежным потокам от инвестирования сегодняшних денег или будущим платежам, необходимым для возврата денег, взятых сегодня в долг.Будущая стоимость (FV) — это стоимость текущего актива на определенную дату в будущем, основанную на предполагаемой скорости роста.Уравнение FV предполагает постоянные темпы роста и единовременный авансовый платеж, который остается нетронутым на протяжении всего периода инвестирования. Расчет справедливой стоимости позволяет инвесторам с разной степенью точности прогнозировать сумму прибыли, которую можно получить от различных инвестиций.
Приведенная стоимость (PV) — это текущая стоимость будущей суммы денег или потока денежных средств при заданной норме прибыли. Приведенная стоимость принимает будущую стоимость и применяет ставку дисконтирования или процентную ставку, которая может быть получена в случае инвестирования.
 Будущая стоимость говорит вам, сколько будет стоить инвестиция в будущем, а текущая стоимость говорит вам, сколько вам нужно в сегодняшних долларах, чтобы заработать определенную сумму в будущем.
Будущая стоимость говорит вам, сколько будет стоить инвестиция в будущем, а текущая стоимость говорит вам, сколько вам нужно в сегодняшних долларах, чтобы заработать определенную сумму в будущем.Критика текущей стоимости
Как указывалось ранее, расчет приведенной стоимости предполагает допущение, что доходность средств может быть получена за определенный период времени. В приведенном выше обсуждении мы рассмотрели одну инвестицию в течение одного года. Однако, если компания решает продолжить серию проектов, которые имеют разную норму доходности для каждого года и каждого проекта, приведенная стоимость становится менее определенной, если эти ожидаемые нормы доходности нереалистичны.Важно учитывать, что при принятии любого инвестиционного решения не гарантируется процентная ставка, а инфляция может снизить доходность инвестиций.
Пример текущей стоимости
Допустим, у вас есть выбор: получать 2 000 долларов сегодня и 3% годовых или 2200 долларов через год.
 Какой вариант лучше?
Какой вариант лучше?- Используя формулу приведенной стоимости, вычисляем: 2200 долларов США / (1 +. 03) 1 = 2135,92 доллара США
- PV = 2135,92 доллара, или минимальная сумма, которую вам нужно будет заплатить сегодня, чтобы через год получить 2200 долларов.Другими словами, если бы вам заплатили 2000 долларов сегодня и исходя из процентной ставки 3%, этой суммы было бы недостаточно, чтобы дать вам 2200 долларов через год.
- В качестве альтернативы вы можете рассчитать будущую стоимость 2 000 долларов сегодня через год: 2 000 x 1,03 = 2060 долларов.
Приведенная стоимость обеспечивает основу для оценки справедливости любых будущих финансовых выгод или обязательств. Например, будущий возврат денежных средств, дисконтированный до приведенной стоимости, может стоить или не стоить потенциально более высокой покупной цены.Тот же финансовый расчет применяется к 0% финансирования при покупке автомобиля.
Выплата процентов по более низкой цене с наклейками может оказаться более выгодной для покупателя, чем уплата нулевых процентов по более высокой цене с наклейками.
 Выплата ипотечных баллов сейчас в обмен на более низкие выплаты по ипотеке в будущем имеет смысл только в том случае, если приведенная стоимость будущих сбережений по ипотеке больше, чем выплаченные сегодня ипотечные баллы.
Выплата ипотечных баллов сейчас в обмен на более низкие выплаты по ипотеке в будущем имеет смысл только в том случае, если приведенная стоимость будущих сбережений по ипотеке больше, чем выплаченные сегодня ипотечные баллы.Часто задаваемые вопросы
Как рассчитать приведенную стоимость?
Приведенная стоимость рассчитывается путем дисконтирования будущих денежных потоков, ожидаемых от инвестиций, до настоящего времени.Для этого инвестору нужны три ключевых точки данных: ожидаемые денежные потоки, количество лет, в течение которых денежные потоки будут выплачиваться, и их ставка дисконтирования. Ставка дисконтирования является очень важным фактором, влияющим на приведенную стоимость, при этом более высокие ставки дисконтирования приводят к более низкой приведенной стоимости, и наоборот. Используя эти переменные, инвесторы могут рассчитать приведенную стоимость по формуле:
Текущее значение знак равно FV ( 1 + р ) п куда: FV знак равно Будущая стоимость р знак равно Норма прибыли п знак равно Количество периодов \ begin {align} & \ text {Present Value} = \ dfrac {\ text {FV}} {(1 + r) ^ n} \\ & \ textbf {где:} \\ & \ text {FV} = \ text {Будущее значение} \\ & r = \ text {Норма прибыли} \\ & n = \ text {Количество периодов} \\ \ end {выровнено} Текущая стоимость = (1 + r) nFV, где: FV = будущий оценщик = норма прибыли n = количество периодов
Какие примеры приведенной стоимости?
В качестве иллюстрации рассмотрим сценарий, в котором вы ожидаете получить единовременную выплату в размере 5000 долларов через пять лет.
 Если ставка дисконтирования составляет 8,25%, вы хотите знать, сколько будет стоить этот платеж сегодня, поэтому вы рассчитываете PV = 5000 долларов США / (1,0825) 5 = 3 363,80.
Если ставка дисконтирования составляет 8,25%, вы хотите знать, сколько будет стоить этот платеж сегодня, поэтому вы рассчитываете PV = 5000 долларов США / (1,0825) 5 = 3 363,80.Почему важна приведенная стоимость?
Приведенная стоимость важна, потому что она позволяет инвесторам судить о том, является ли цена, которую они платят за инвестиции, уместной. Например, в нашем предыдущем примере ставка дисконтирования 12% снизила бы приведенную стоимость инвестиций только до 1802,39 доллара. В этом сценарии мы бы очень неохотно платили за инвестиции больше этой суммы, поскольку наш расчет приведенной стоимости показывает, что мы могли бы найти лучшие возможности в другом месте.Подобные расчеты приведенной стоимости играют решающую роль в таких областях, как инвестиционный анализ, управление рисками и финансовое планирование.
финансовых формул (с калькуляторами)
Люди из всех слоев общества, от студентов, биржевых маклеров и банкиров; риэлторам, домовладельцам и управляющим находят финансовые формулы невероятно полезными в повседневной жизни.
 Независимо от того, используете ли вы финансовые формулы для личных или
по причинам образования, наличие доступа к правильным финансовым формулам может помочь улучшить вашу жизнь.
Независимо от того, используете ли вы финансовые формулы для личных или
по причинам образования, наличие доступа к правильным финансовым формулам может помочь улучшить вашу жизнь.Независимо от того, в какой финансовой сфере вы работаете или изучаете, от корпоративных финансов до банковского дела, все они построены на тот же фундамент стандартных формул и уравнений. Хотя некоторые из этих сложных формул могут сбить с толку обычного человека, мы помогите, внося вам ясность.
Имеете ли вы дело со сложными процентами, аннуитетами, акциями или облигациями, инвесторы должны иметь возможность эффективно оценивать уровень ценности или достоинства их финансовых показателей.Это делается путем оценки будущей прибыли и ее расчета относительно текущая стоимость или эквивалентная норма прибыли.
FinanceFormulas.net может помочь.
Финансовая информация и калькуляторы на сайте FinanceFormulas.
 net предназначены не только для профессионалов, но и для всех, кто
потребность в фундаментальных формулах, уравнениях и основных вычислениях, составляющих мир финансов. От студентов колледжа
которые изучают финансы и бизнес, до профессионалов, занимающихся корпоративными финансами, FinanceFormulas.сеть
поможет вам найти финансовые формулы, уравнения и калькуляторы, необходимые для достижения успеха.
net предназначены не только для профессионалов, но и для всех, кто
потребность в фундаментальных формулах, уравнениях и основных вычислениях, составляющих мир финансов. От студентов колледжа
которые изучают финансы и бизнес, до профессионалов, занимающихся корпоративными финансами, FinanceFormulas.сеть
поможет вам найти финансовые формулы, уравнения и калькуляторы, необходимые для достижения успеха.Кто может получить больше всего от FinanceFormulas.net?
Студенты, изучающие финансы и бизнес, могут использовать формулы и калькуляторы, бесплатно предоставляемые FinanceFormulas.net в качестве постоянного справочника, во время учебы в школе, затем во время работы в мир финансов.
Люди, уже работающие в сфере бизнеса , которые могут иметь Если вы забыли, как использовать определенную формулу или набор уравнений, наши инструменты станут бесценным ресурсом.
 FinanceFormulas.net не только
упрощает поиск формулы, уравнения или калькулятора, которые вы ищете, мы упрощаем добавление формулы в закладки, чтобы вы
больше никогда не придется тратить время на поиск нужного инструмента.
FinanceFormulas.net не только
упрощает поиск формулы, уравнения или калькулятора, которые вы ищете, мы упрощаем добавление формулы в закладки, чтобы вы
больше никогда не придется тратить время на поиск нужного инструмента.Кто угодно . Люди любого возраста могут пользоваться калькуляторами в FinanceFormulas.net, чтобы помочь им справляться с финансовыми трудностями повседневной жизни. Ипотека, задолженность по кредитной карте или понимание академической оценки вашего инвестиции, такие как акции и облигации, он имеет доступ к правильным формулам, уравнениям и калькуляторам, которые могут помочь вам проложите свой путь к финансово благополучной жизни.
Планируете ли вы использовать бесплатные формулы, предоставляемые FinanceFormulas.net, для личного или академического использования, FinanceFormulas.net здесь, чтобы помочь вам найти банковские формулы, формулы акций и облигаций, корпоративные и прочие.
 формулы, которые вам нужны.
формулы, которые вам нужны.
Вернуться к началуТекущая стоимость (PV)
Деньги сейчас дороже денег позже .Почему? Потому что вы можете использовать деньги, чтобы зарабатывать больше!
Вы можете вести бизнес, или купить что-то сейчас, а потом продать дороже, или просто положить деньги в банк, чтобы заработать проценты.
Пример: Вы можете получить 10% годовых на свои деньги.
Итак, 1000 долларов сейчас может заработать 1000 долларов x 10% = 100 долларов в год.
Ваши 1000 долларов сейчас могут стать 1100 долларов через год .
Текущая стоимость
Таким образом, 1000 долларов сейчас равняются таким же , как 1100 долларов в следующем году (при 10% -ной процентной ставке).Мы говорим, что приведенная стоимость в размере 1100 долларов в следующем году составит 1000 долларов
Потому что мы могли бы превратить 1000 долларов в 1100 долларов (если бы мы могли заработать 10%).

А теперь давайте расширим эту идею в будущее …
Как рассчитать будущие платежи
Давайте останемся с 10% годовых. Это означает, что деньги растут на 10% каждый год, например:
Итак:
- 1100 долларов в следующем году то же самое, что и 1000 долларов сейчас .
- И 1210 долларов через 2 года это то же самое, что 1000 долларов сейчас .
- и т. Д.
Фактически все эти суммы равны (с учетом , когда они возникают, и 10% -ной доли).
Более простой расчет
Но вместо «прибавления 10% к каждому году» проще умножить на 1,10 (объяснено в разделе «Сложный процент»):
Итак, мы получаем это (тот же результат, что и выше):
Назад в будущее
И чтобы посмотреть, сколько денег в будущем стоит сейчас , вернитесь назад (разделив на 1.10 каждый год вместо умножения):
Пример: Сэм обещает вам
500 долларов в следующем году , какова текущая стоимость?Чтобы перенести будущий платеж назад на один год разделите на 1,10
Итак, 500 долларов в следующем году это 500 долларов ÷ 1,10 = 454,55 долларов сейчас (с точностью до цента).

Текущая стоимость $ 454,55
Пример: Алекс обещает вам
900 долларов через 3 года , какова текущая стоимость?Чтобы отсчитать будущий платеж назад на три года разделите на 1.10 трижды
Итак 900 долларов за 3 года это:
$ 900 ÷ 1.10 ÷ 1.10 ÷ 1.10
$ 900 ÷ (1,10 × 1,10 × 1,10)
$ 900 ÷ 1,331
676,18 $ сейчас (с точностью до цента).
Лучше с экспонентами
Но вместо $ 900 ÷ (1,10 × 1,10 × 1,10) лучше использовать экспоненты (показатель степени говорит , сколько раз использовать при умножении).
Пример: (продолжение)
Текущая стоимость 900 долларов за 3 года (за один раз):
$ 900 ÷ 1,10 3 = 676,18 $ сейчас (с точностью до цента).
Как формула это:
PV = FV / (1 + r) n
- PV — текущая стоимость
- FV — будущая стоимость
- r — процентная ставка (в десятичном формате, поэтому 0.
 10, а не 10%) 900 10
10, а не 10%) 900 10 - n — количество лет
Пример: (продолжение)
Используйте формулу для расчета приведенной стоимости 900 долларов за 3 года :
PV = FV / (1 + r) n
PV = 900 долларов США / (1 + 0,10) 3 = 900 долларов США / 1,10 3 = 676,18 долларов США (с точностью до цента).
Показатели проще использовать, особенно с калькулятором.
Например, 1,10 6 быстрее, чем 1,10 × 1,10 × 1,10 × 1,10 × 1,10 × 1,10
Давайте еще немного воспользуемся формулой:
Пример: Сколько сейчас стоит 570 долларов в следующем году при процентной ставке 10%?
PV = 570 долларов США / (1 + 0,10) 1 = 570 долларов США / 1,10 = долларов США 518,18 долларов США (с точностью до цента)
Но ваш выбор процентной ставки может все изменить!
Пример: Сколько сейчас стоит 570 долларов в следующем году при процентной ставке 15%?
ЛС = 570 долл.
 США / (1 + 0.15) 1 = 570 долларов / 1,15 = 495,65 долларов (с точностью до цента)
США / (1 + 0.15) 1 = 570 долларов / 1,15 = 495,65 долларов (с точностью до цента)Или что делать, если не получишь деньги 3 года
Пример: Сколько сейчас стоит 570 долларов через 3 года при процентной ставке 10%?
PV = 570 долларов США / (1 + 0,10) 3 = 570 долларов США / 1,331 = 428,25 долларов США (с точностью до цента)
Последний пример:
Пример: Вам обещают 800 долларов через 10 лет. Какова его текущая стоимость при процентной ставке 6%?
ЛС = 800 $ / (1 + 0.06) 10 = 800 долл. США / 1,7908 … = 446,72 долл. США (с точностью до цента)
Расчет приведенной стоимости | AccountingCoach
Самый простой и точный способ рассчитать текущую стоимость любых будущих сумм (единичная сумма, различные суммы, аннуитеты) — использовать электронный финансовый калькулятор или компьютерное программное обеспечение. Некоторые электронные финансовые калькуляторы теперь доступны менее чем за 35 долларов.

ВАЖНО! Поймите, что каждый финансовый калькулятор работает по-своему и может работать не так, как в нашем Разъяснении.Обязательно прочтите и полностью усвойте инструкции перед использованием любого калькулятора или компьютерного программного обеспечения. Одно неверное предположение, один неверный ввод или использование кнопки, которая работает не так, как вы предполагали, будет означать неправильный ответ — а это может иметь значительные финансовые последствия!
Если у вас нет доступа к электронному финансовому калькулятору или программному обеспечению, простой способ рассчитать суммы приведенной стоимости — использовать таблицы приведенной стоимости (таблицы PV).Таблицы PV не могут обеспечить такой же уровень точности, как финансовые калькуляторы или компьютерное программное обеспечение, потому что коэффициенты, используемые в таблицах, округлены до меньшего числа десятичных знаков. Кроме того, они обычно содержат ограниченное количество вариантов процентных ставок и периодов времени.
 Несмотря на это, таблицы приведенной стоимости остаются популярными в академической среде, поскольку их легко включить в учебник. Поскольку они широко используются, мы будем использовать таблицы приведенной стоимости для решения наших примеров.
Несмотря на это, таблицы приведенной стоимости остаются популярными в академической среде, поскольку их легко включить в учебник. Поскольку они широко используются, мы будем использовать таблицы приведенной стоимости для решения наших примеров.За каждой таблицей, калькулятором и программным обеспечением стоят математических формул , необходимых для вычисления сумм приведенной стоимости, процентных ставок, количества периодов и сумм будущей стоимости.Вначале мы покажем вам несколько примеров того, как использовать формулу приведенной стоимости в дополнение к таблицам PV.
За исключением незначительных различий из-за округления, ответы на приведенные ниже уравнения будут одинаковыми, независимо от того, вычисляются ли они с помощью финансового калькулятора, компьютерного программного обеспечения, таблиц PV или формул.
Расчет текущей стоимости единой суммы (PV)
В этом разделе мы покажем, как найти текущую стоимость одной будущей денежной суммы, такой как квитанция или платеж.
 Мы будем ссылаться на приведенную стоимость одной суммы как PV .
Мы будем ссылаться на приведенную стоимость одной суммы как PV .Упражнение № 1
Предположим, мы должны получить 100 долларов в конце двух лет. Как рассчитать приведенную стоимость суммы, предполагая, что процентная ставка составляет 8% годовых, начисляемых ежегодно?
На следующей временной шкале изображена известная нам информация вместе с неизвестным компонентом (PV):
Расчет по формуле PV
Формула приведенной стоимости для отдельной суммы:
Используя вторую версию формулы, решение:
Ответ, 85 $.73 , говорит нам, что получить 100 долларов через два года — это то же самое, что получить 85,73 доллара сегодня, если временная стоимость денег составляет 8% годовых, начисленных ежегодно. («Сегодня» — это то же понятие, что и «период времени 0»)
Расчет с использованием PV 1 Таблица
Обычно в учебниках по бухгалтерскому учету и финансам приводятся таблицы приведенной стоимости для использования при расчете сумм приведенной стоимости.
 В таблице PV, равной 1, каждый заголовок столбца отображает процентную ставку (i), а строка указывает количество периодов в будущем, прежде чем возникнет сумма (n).На пересечении каждого столбца и строки находится коррелирующее приведенное значение коэффициента 1 (PV = 1). Фактор PV 1 говорит нам, какой будет приведенная стоимость в период времени 0 для одной суммы в 1 доллар в конце периода времени (n). Щелкните следующее, чтобы увидеть приведенную стоимость 1 таблицы: PV из 1 таблицы .
В таблице PV, равной 1, каждый заголовок столбца отображает процентную ставку (i), а строка указывает количество периодов в будущем, прежде чем возникнет сумма (n).На пересечении каждого столбца и строки находится коррелирующее приведенное значение коэффициента 1 (PV = 1). Фактор PV 1 говорит нам, какой будет приведенная стоимость в период времени 0 для одной суммы в 1 доллар в конце периода времени (n). Щелкните следующее, чтобы увидеть приведенную стоимость 1 таблицы: PV из 1 таблицы .PV таблицы 1 имеет два ограничения: (1) значения округляются (в нашей таблице округлено до трех знаков после запятой для простоты использования), и, таким образом, таблица немного жертвует точностью, и (2) таблица отображает только ограниченное количество знаков после запятой. количество вариантов ставок и лет.
После определения PV 1 фактора из таблицы просто используйте его для замены следующего члена в формуле PV: [1 ÷ (1 + i) n ]
Используя данные, представленные в Упражнении № 1, мы можем определить приведенную стоимость получения 100 долларов в конце двух лет с дисконтированием по процентной ставке 8% годовых:
Поскольку для PV 1 таблицы были округлены коэффициенты до трех десятичных знаков, ответ (85,70 долларов США) немного отличается от суммы, рассчитанной по формуле PV (85 долларов США.
 73). В любом случае ответ говорит нам, что 100 долларов в конце двух лет эквивалентны получению примерно 85,70 доллара сегодня (в период времени 0), если временная стоимость денег составляет 8% в год, усугубляемых ежегодно.
73). В любом случае ответ говорит нам, что 100 долларов в конце двух лет эквивалентны получению примерно 85,70 доллара сегодня (в период времени 0), если временная стоимость денег составляет 8% в год, усугубляемых ежегодно.Упражнение № 2
Нам необходимо рассчитать приведенную стоимость (стоимость в период времени 0) получения единовременной суммы в 1000 долларов за 20 лет. Процентная ставка дисконтирования будущей суммы оценивается в 10% годовых, начисленных ежегодно.
На следующей временной шкале изображена известная нам информация вместе с неизвестным компонентом (PV):
Расчет с использованием формулы PV 1
Используя формулу для определения приведенной стоимости, мы имеем:Ответ говорит нам, что получение 1000 долларов через 20 лет эквивалентно получению 148 долларов.64 сегодня, если временная стоимость денег составляет 10% годовых, начисленных ежегодно.
Расчет с использованием PV 1 Таблица
Используйте таблицу PV 1, чтобы найти (округленный) коэффициент текущей стоимости на пересечении n = 20 и i = 10%. Чтобы рассчитать приведенную стоимость получения 1000 долларов США по истечении 20 лет с процентной ставкой 10%, введите коэффициент в формулу:
Чтобы рассчитать приведенную стоимость получения 1000 долларов США по истечении 20 лет с процентной ставкой 10%, введите коэффициент в формулу:Мы видим, что приведенная стоимость получения 1000 долларов через 20 лет эквивалентна получению примерно 149 долларов.00 сегодня, если временная стоимость денег составляет 10% годовых, начисленных ежегодно.
Упражнение № 3
Какова приведенная стоимость получения единовременной суммы в 5000 долларов по истечении трех лет, если временная стоимость денег составляет 8% в год, составляющих ежеквартально ?
На следующей временной шкале изображена известная нам информация вместе с неизвестным компонентом (PV):
Обратите внимание, что на временной шкале показано n = 12, потому что в трехлетнем периоде 12 кварталов.Поскольку периоды времени составляют три месяца, ставка дисконтирования составляет i = 2% (квартальная ставка , которая получается из годовой ставки 8%, деленной на четыре квартала каждого года).

Расчет с использованием формулы PV
Используя формулу для определения приведенной стоимости, мы имеем:Ответ говорит нам, что получение 5000 долларов через три года после сегодняшнего дня эквивалентно получению 3942,45 доллара сегодня, если временная стоимость денег составляет 8% годовых, что составляет квартальных .
Расчет с использованием PV 1 Таблица
Приведенная стоимость получения 5000 долларов в конце трех лет, когда процентная ставка начисляется ежеквартально , требует, чтобы (n) и (i) были указаны в кварталах. Используйте PV из 1 таблицы , чтобы найти (округленную) приведенную стоимость на пересечении n = 12 (3 года x 4 квартала) и i = 2% (8% в год ÷ 4 квартала). Подставьте коэффициент в формулу:Мы видим, что приведенная стоимость получения 5000 долларов через три года после сегодняшнего дня составляет примерно 3940 долларов.00, если временная стоимость денег составляет 8% в год, начисляется ежеквартально.
Упражнение № 4
Какова приведенная стоимость получения единовременной суммы в размере 10 000 долларов в конце пяти лет, если временная стоимость денег составляет 6% в год, составляющих за полгода?
На следующей временной шкале изображена известная нам информация вместе с неизвестным компонентом (PV):
Обратите внимание, что на временной шкале показано n = 10, потому что в пятилетнем периоде 10 шестимесячных (или полугодовых) периодов.Поскольку начисление сложных процентов происходит раз в полгода, ставка дисконтирования составляет i = 3% за шестимесячный период (годовая ставка 6%, деленная на два полугодовых периода в каждом году).
Расчет с использованием формулы PV
Используя формулу для определения приведенной стоимости, мы имеем:Ответ говорит нам, что получение 10 000 долларов через пять лет после сегодняшнего дня эквивалентно получению 7 440,90 долларов сегодня, если временная стоимость денег составляет 6% годовых, составляющих за полугодие.
Расчет с использованием PV 1 Таблица
Для приведенной стоимости получения 10000 долларов в конце пяти лет, когда начисление сложных процентов является полугодовым, необходимо, чтобы n = 10 (5 лет X 2 полугодовых периода в год) и i = 3% (6% в год ÷ два полугодовых периода в каждом году). Используйте PV из 1 таблицы , чтобы найти (округленный) коэффициент приведенной стоимости на пересечении n = 10 и i = 3%. Подставьте коэффициент в формулу:Мы видим, что приведенная стоимость получения 10 000 долларов через пять лет эквивалентна получению примерно 7 440 долларов.00:00 сегодня, если временная стоимость денег составляет 6% в год, составила за полугодие .
Калькулятор текущей стоимости
Этот калькулятор текущей стоимости может использоваться для расчета текущей стоимости определенной суммы денег в будущем или периодических аннуитетных платежах.
Текущая стоимость будущих денег
Результаты
Текущая стоимость: $ 558,39
Общая сумма процентов: 441 $.61
Текущая стоимость периодических вкладов
- Приведенная стоимость означает, что сумма денег сегодня стоит больше, чем такая же сумма в будущем.

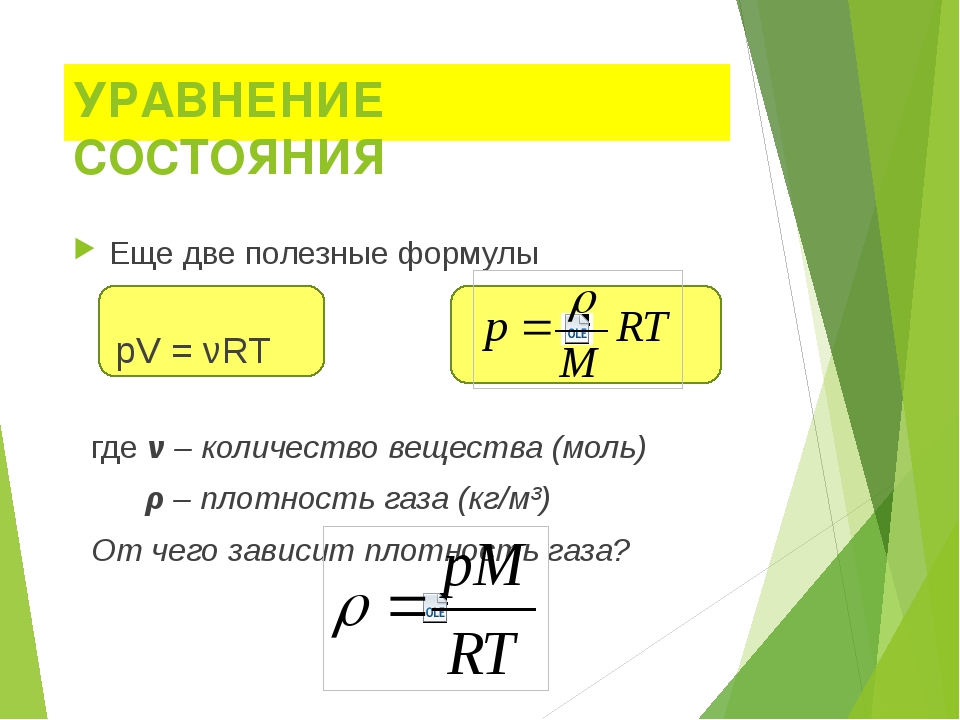 {-N} \over r \right] (1+r) } \)
{-N} \over r \right] (1+r) } \) {19}} \over 0.07 \right] \end{aligned} } \)
{19}} \over 0.07 \right] \end{aligned} } \) {30}} \over 0.05 \right] \end{aligned} } \)
{30}} \over 0.05 \right] \end{aligned} } \) t \right] } \) (формула 12)
t \right] } \) (формула 12) В примере выше первый платеж произошел при t = 1; поэтому мы вычисляем текущую стоимость при t = 0.
В примере выше первый платеж произошел при t = 1; поэтому мы вычисляем текущую стоимость при t = 0.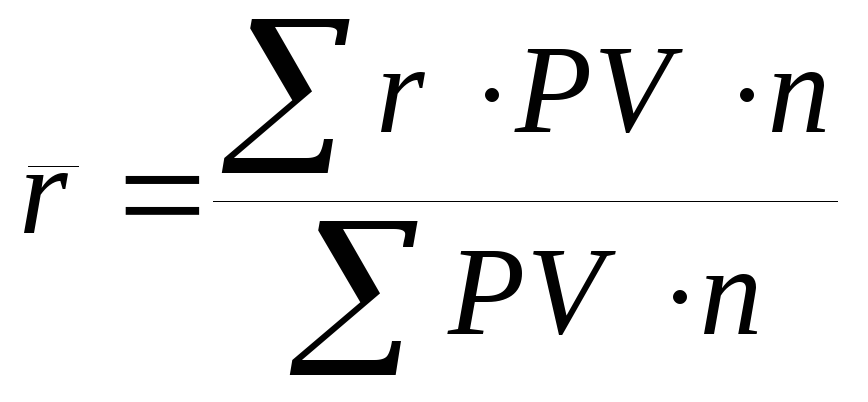 05
05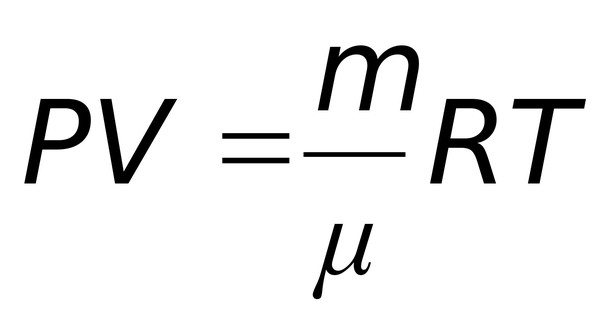




 38
38 46
46 В качестве значения аргумента «ставка» нужно ввести в формулу 10%/12, 0,83% или 0,0083.
В качестве значения аргумента «ставка» нужно ввести в формулу 10%/12, 0,83% или 0,0083. Если аргумент «бс» опущен, предполагается, что он равен 0 (например, будущая стоимость для займа равна 0).
Если аргумент «бс» опущен, предполагается, что он равен 0 (например, будущая стоимость для займа равна 0). Определение подходящей ставки дисконтирования является ключом к правильной оценке будущих денежных потоков, будь то прибыль или долговые обязательства.
Определение подходящей ставки дисконтирования является ключом к правильной оценке будущих денежных потоков, будь то прибыль или долговые обязательства.
 Формула приведенной стоимости дисконтирует будущую стоимость к сегодняшним долларам, принимая во внимание предполагаемую годовую ставку либо из инфляции, либо из нормы прибыли, которая могла бы быть достигнута, если бы сумма была инвестирована.
Формула приведенной стоимости дисконтирует будущую стоимость к сегодняшним долларам, принимая во внимание предполагаемую годовую ставку либо из инфляции, либо из нормы прибыли, которая могла бы быть достигнута, если бы сумма была инвестирована. доходности , инвестиции должны приносить как минимум более 2%, чтобы оправдать риск.
доходности , инвестиции должны приносить как минимум более 2%, чтобы оправдать риск. n} \\ & \ textbf {где:} \\ & \ text {FV} = \ text {Будущее значение} \\ & r = \ text {Норма прибыли} \\ & n = \ text {Количество периодов} \\ \ end {выровнено}Взаимодействие с другими людьмиТекущее значениезнак равно(1+г)п
n} \\ & \ textbf {где:} \\ & \ text {FV} = \ text {Будущее значение} \\ & r = \ text {Норма прибыли} \\ & n = \ text {Количество периодов} \\ \ end {выровнено}Взаимодействие с другими людьмиТекущее значениезнак равно(1+г)п Проще говоря, с течением времени деньги сегодня стоят больше, чем те же деньги завтра. Будущая стоимость может относиться к будущим денежным поступлениям от инвестирования сегодняшних денег или будущим платежам, необходимым для возврата денег, взятых сегодня в долг.
Проще говоря, с течением времени деньги сегодня стоят больше, чем те же деньги завтра. Будущая стоимость может относиться к будущим денежным поступлениям от инвестирования сегодняшних денег или будущим платежам, необходимым для возврата денег, взятых сегодня в долг.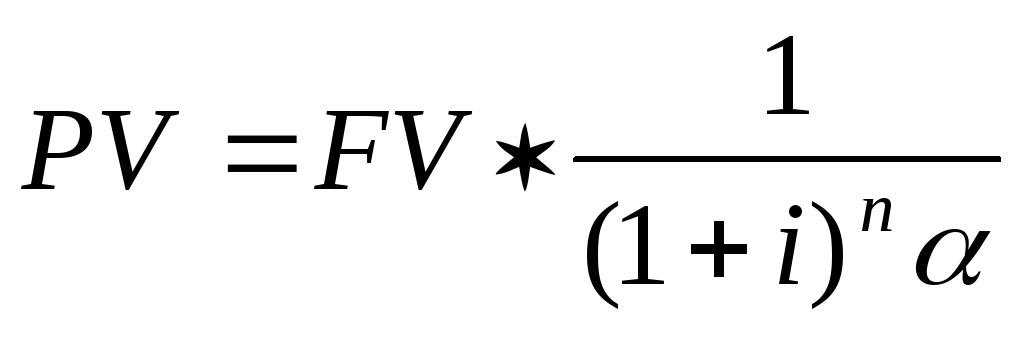
 1.
1.
 Применяя нашу формулу приведенной стоимости, мы получим приведенную стоимость в 2106,18 долларов. Другими словами, если бы кто-то спросил нас, сколько стоит эта инвестиция, мы бы ответили, что она стоит не более 2106,18 долларов. С другой стороны, если бы наша ставка дисконтирования составляла 12,00%, то ее приведенная стоимость была бы намного ниже, что сделало бы цену в 2 106,18 доллара слишком высокой.
Применяя нашу формулу приведенной стоимости, мы получим приведенную стоимость в 2106,18 долларов. Другими словами, если бы кто-то спросил нас, сколько стоит эта инвестиция, мы бы ответили, что она стоит не более 2106,18 долларов. С другой стороны, если бы наша ставка дисконтирования составляла 12,00%, то ее приведенная стоимость была бы намного ниже, что сделало бы цену в 2 106,18 доллара слишком высокой.


 Periods
Periods  То, что вы должны использовать, — это формула PV.
То, что вы должны использовать, — это формула PV.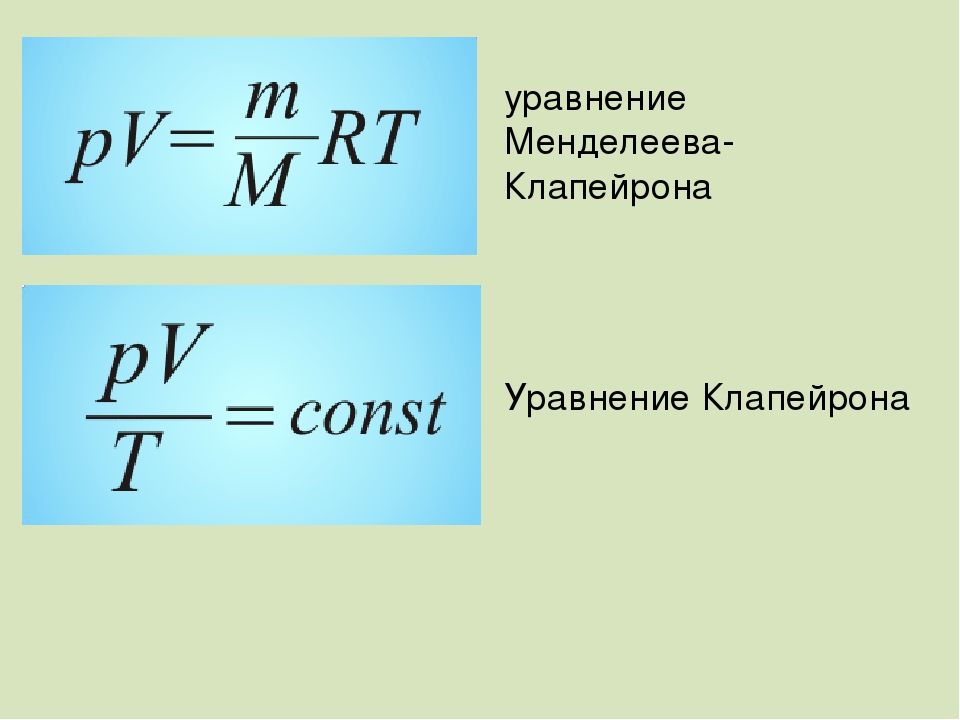 3 = 100 тысяч.
3 = 100 тысяч. У меня есть формула, но расчеты показывают неверные. Его процентная ставка 6% на период 30 лет, конечное значение — 833333. Правильный…
У меня есть формула, но расчеты показывают неверные. Его процентная ставка 6% на период 30 лет, конечное значение — 833333. Правильный… Я застрял на преобразовании функции Excel FV, которая определяется таким образом: FV( interest_rate, number_payments,…
Я застрял на преобразовании функции Excel FV, которая определяется таким образом: FV( interest_rate, number_payments,… ..
..


 Так, например, если двухлетнее казначейство выплачивает 2% годовых или доходность, инвестиции должны приносить как минимум более 2%, чтобы оправдать риск.
Так, например, если двухлетнее казначейство выплачивает 2% годовых или доходность, инвестиции должны приносить как минимум более 2%, чтобы оправдать риск. n} \\ & \ textbf {где:} \\ & \ text {FV} = \ text {Будущее значение} \\ & r = \ text {Норма прибыли} \\ & n = \ text {Количество периодов} \\ \ end {выровнено}
Текущая стоимость = (1 + r) nFV, где: FV = будущий оценщик = норма прибыли n = количество периодов
n} \\ & \ textbf {где:} \\ & \ text {FV} = \ text {Будущее значение} \\ & r = \ text {Норма прибыли} \\ & n = \ text {Количество периодов} \\ \ end {выровнено}
Текущая стоимость = (1 + r) nFV, где: FV = будущий оценщик = норма прибыли n = количество периодов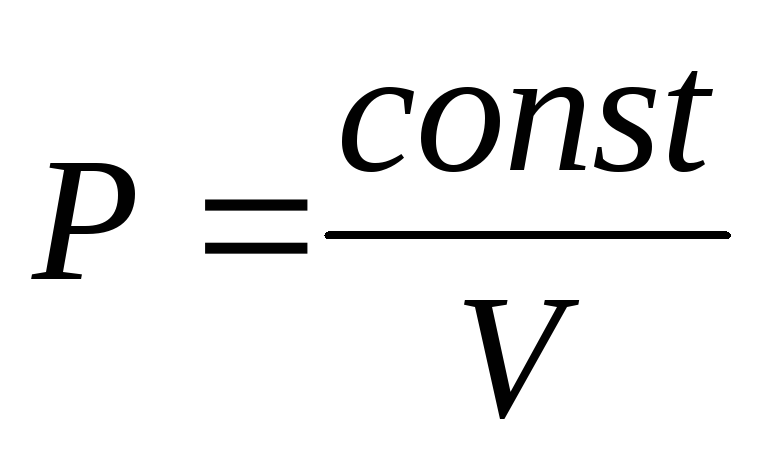 Проще говоря, с течением времени деньги сегодня стоят больше, чем те же деньги завтра. Будущая стоимость может относиться к будущим денежным потокам от инвестирования сегодняшних денег или будущим платежам, необходимым для возврата денег, взятых сегодня в долг.
Проще говоря, с течением времени деньги сегодня стоят больше, чем те же деньги завтра. Будущая стоимость может относиться к будущим денежным потокам от инвестирования сегодняшних денег или будущим платежам, необходимым для возврата денег, взятых сегодня в долг. Будущая стоимость говорит вам, сколько будет стоить инвестиция в будущем, а текущая стоимость говорит вам, сколько вам нужно в сегодняшних долларах, чтобы заработать определенную сумму в будущем.
Будущая стоимость говорит вам, сколько будет стоить инвестиция в будущем, а текущая стоимость говорит вам, сколько вам нужно в сегодняшних долларах, чтобы заработать определенную сумму в будущем. Какой вариант лучше?
Какой вариант лучше? Выплата ипотечных баллов сейчас в обмен на более низкие выплаты по ипотеке в будущем имеет смысл только в том случае, если приведенная стоимость будущих сбережений по ипотеке больше, чем выплаченные сегодня ипотечные баллы.
Выплата ипотечных баллов сейчас в обмен на более низкие выплаты по ипотеке в будущем имеет смысл только в том случае, если приведенная стоимость будущих сбережений по ипотеке больше, чем выплаченные сегодня ипотечные баллы.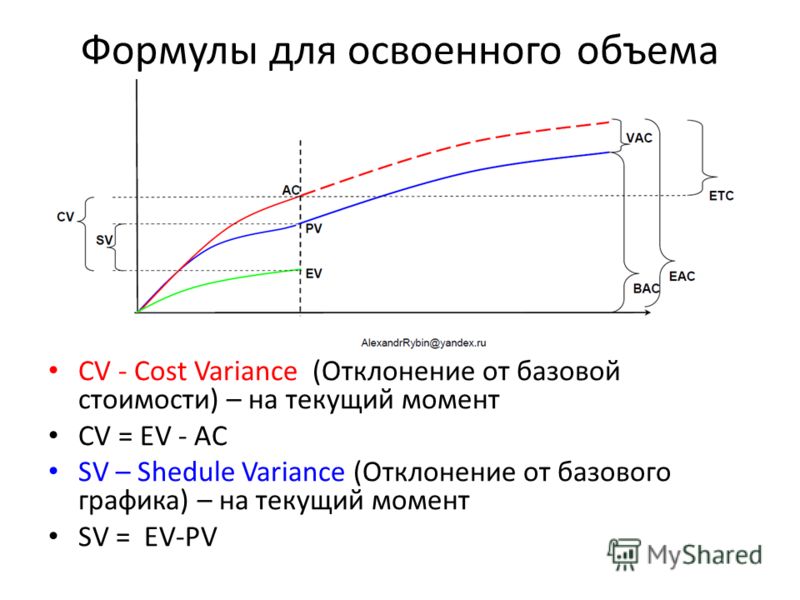 Если ставка дисконтирования составляет 8,25%, вы хотите знать, сколько будет стоить этот платеж сегодня, поэтому вы рассчитываете PV = 5000 долларов США / (1,0825) 5 = 3 363,80.
Если ставка дисконтирования составляет 8,25%, вы хотите знать, сколько будет стоить этот платеж сегодня, поэтому вы рассчитываете PV = 5000 долларов США / (1,0825) 5 = 3 363,80. Независимо от того, используете ли вы финансовые формулы для личных или
по причинам образования, наличие доступа к правильным финансовым формулам может помочь улучшить вашу жизнь.
Независимо от того, используете ли вы финансовые формулы для личных или
по причинам образования, наличие доступа к правильным финансовым формулам может помочь улучшить вашу жизнь. net предназначены не только для профессионалов, но и для всех, кто
потребность в фундаментальных формулах, уравнениях и основных вычислениях, составляющих мир финансов. От студентов колледжа
которые изучают финансы и бизнес, до профессионалов, занимающихся корпоративными финансами, FinanceFormulas.сеть
поможет вам найти финансовые формулы, уравнения и калькуляторы, необходимые для достижения успеха.
net предназначены не только для профессионалов, но и для всех, кто
потребность в фундаментальных формулах, уравнениях и основных вычислениях, составляющих мир финансов. От студентов колледжа
которые изучают финансы и бизнес, до профессионалов, занимающихся корпоративными финансами, FinanceFormulas.сеть
поможет вам найти финансовые формулы, уравнения и калькуляторы, необходимые для достижения успеха. FinanceFormulas.net не только
упрощает поиск формулы, уравнения или калькулятора, которые вы ищете, мы упрощаем добавление формулы в закладки, чтобы вы
больше никогда не придется тратить время на поиск нужного инструмента.
FinanceFormulas.net не только
упрощает поиск формулы, уравнения или калькулятора, которые вы ищете, мы упрощаем добавление формулы в закладки, чтобы вы
больше никогда не придется тратить время на поиск нужного инструмента. формулы, которые вам нужны.
формулы, которые вам нужны.

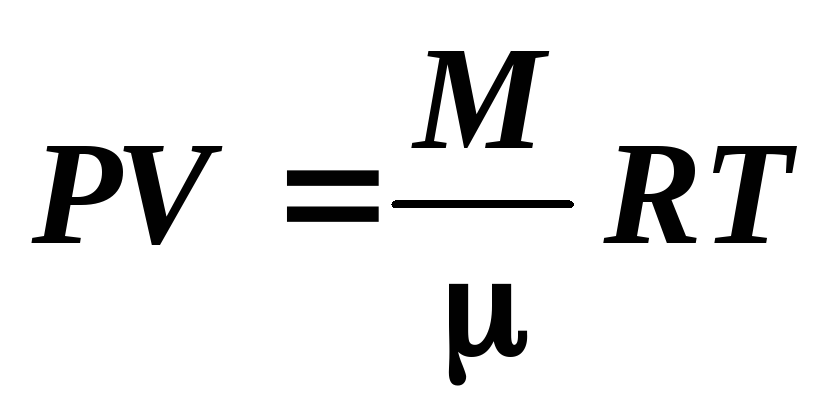 10, а не 10%) 900 10
10, а не 10%) 900 10 США / (1 + 0.15) 1 = 570 долларов / 1,15 = 495,65 долларов (с точностью до цента)
США / (1 + 0.15) 1 = 570 долларов / 1,15 = 495,65 долларов (с точностью до цента)
 Несмотря на это, таблицы приведенной стоимости остаются популярными в академической среде, поскольку их легко включить в учебник. Поскольку они широко используются, мы будем использовать таблицы приведенной стоимости для решения наших примеров.
Несмотря на это, таблицы приведенной стоимости остаются популярными в академической среде, поскольку их легко включить в учебник. Поскольку они широко используются, мы будем использовать таблицы приведенной стоимости для решения наших примеров. Мы будем ссылаться на приведенную стоимость одной суммы как PV .
Мы будем ссылаться на приведенную стоимость одной суммы как PV . В таблице PV, равной 1, каждый заголовок столбца отображает процентную ставку (i), а строка указывает количество периодов в будущем, прежде чем возникнет сумма (n).На пересечении каждого столбца и строки находится коррелирующее приведенное значение коэффициента 1 (PV = 1). Фактор PV 1 говорит нам, какой будет приведенная стоимость в период времени 0 для одной суммы в 1 доллар в конце периода времени (n). Щелкните следующее, чтобы увидеть приведенную стоимость 1 таблицы: PV из 1 таблицы .
В таблице PV, равной 1, каждый заголовок столбца отображает процентную ставку (i), а строка указывает количество периодов в будущем, прежде чем возникнет сумма (n).На пересечении каждого столбца и строки находится коррелирующее приведенное значение коэффициента 1 (PV = 1). Фактор PV 1 говорит нам, какой будет приведенная стоимость в период времени 0 для одной суммы в 1 доллар в конце периода времени (n). Щелкните следующее, чтобы увидеть приведенную стоимость 1 таблицы: PV из 1 таблицы . 73). В любом случае ответ говорит нам, что 100 долларов в конце двух лет эквивалентны получению примерно 85,70 доллара сегодня (в период времени 0), если временная стоимость денег составляет 8% в год, усугубляемых ежегодно.
73). В любом случае ответ говорит нам, что 100 долларов в конце двух лет эквивалентны получению примерно 85,70 доллара сегодня (в период времени 0), если временная стоимость денег составляет 8% в год, усугубляемых ежегодно. Чтобы рассчитать приведенную стоимость получения 1000 долларов США по истечении 20 лет с процентной ставкой 10%, введите коэффициент в формулу:
Чтобы рассчитать приведенную стоимость получения 1000 долларов США по истечении 20 лет с процентной ставкой 10%, введите коэффициент в формулу:
Об авторе