Как посчитать чистый дисконтированный доход: Как рассчитать чистый дисконтированный доход (формула)
Формула чистого дисконтированного дохода
Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.
Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!
Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Главная Справочник Формулы по экономике Формула чистого дисконтированного дохода
Понятие чистого дисконтированного дохода
Формула чистого дисконтированного дохода помогает произвести оценку собственной экономической эффективности проекта, при этом сравнить объекты для инвестирования.
В нашей стране используется показатель ЧДД, а NPV является основным показателем, который применяется в инвестиционном анализе в процессе выбора объекта инвестирования.
Формула чистого дисконтированного дохода
Формула чистого дисконтированного дохода включает в себя все входящие потоки, из которых за каждый промежуток времени последовательновычитают исходящие потоки. При этом происходит их дисконтирование, то есть приведение стоимости суммы всех потоков на момент расчета. Эти действия позволяют рассчитать чистый дисконтированный доход.
Формула чистого дисконтированного дохода выглядит следующим образом:
NPV (ЧДД) = — IC + ƩCFt/ (1 + i)t
Здесь IC – первоначальная сумма инвестиций (те средства, которые планируют вложить в проект),
CFt – суммарный денежный поток периода t,
i – ставка приведения (дисконтирования).
Особенности расчета формулы ЧДД
Главной особенностью расчетов по формуле чистого дисконтированного дохода является включение в исходящие потоки суммы инвестиций, не зависимо от момента времени. Инвестиции могут быть произведены на протяжении действия проекта не один раз, а не только на этапе его реализации.
Формула чистого дисконтированного дохода, рассчитанная с положительным значением, говорит о том, что с учетом альтернативных вложений проект эффективен.
Формула чистого дисконтированного дохода включает в себя следующие составляющие, которые имеют свои особенности:
- Первоначальная сумма инвестиций(IC), которая берется в отрицательном значении, поскольку является затратами на осуществление проекта, прибыль от которых будет в будущем. Поскольку инвестиции часто осуществляются не за один момент, их также следует дисконтировать, учитывая фактор времени.
- Денежный поток(CFt), который распределяет с учетом временного фактора все притоки и оттоки за каждый период. Он изменяется от 1 до п (здесь п – длительность проекта инвестиций).
- Ставка дисконта или процента (i), применяемая с целью дисконтирования всех будущих поступлений в единую сумму стоимости текущего момента.
Значения показателя ЧДД
Существует 3 значения показателя чистого дисконтированного дохода:
- ЧДД> 0
В этой ситуации можно говорить о выгодности инвестиционных вложений. Но окончательное решение инвестор может принять лишь тогда, когда сравнит данное значение с другими объектами для инвестирования.
Но окончательное решение инвестор может принять лишь тогда, когда сравнит данное значение с другими объектами для инвестирования.
- ЧДД < 0
В этом случае можно сказать, что вложения инвесторов не принесут прибыли, поэтому стоит отказаться от вложений в проект.
- ЧДД = 0
Если чистый дисконтированный доход будет нулевым, то говорят о том, что инвесторы на таком проекте ничего не заработают, но и не потеряют. Со временем данный проект может начать приносить прибыль, но в большинстве случаев инвесторы от них отказываются. Данный проект можно принять во внимание, если помимо финансовой цели, инвесторы преследуют другие интересы (например, при реализации социально-значимых проектов).
Значение показателя чистого дисконтированного дохода
Формула чистого дисконтированного дохода чаще всего применяется для анализа эффективности проекта, при этом обычно происходит сравнение нескольких проектов друг с другом.
Положительное значение показателя показывает, что проект выгоден к реализации, чем вкладв другие активы с такими же сроками и параметрами риска. Чистый дисконтированный доход основывается на прогнозах денежных потоков, подверженных рискам и формируемых в условиях неопределенности.
Чистый дисконтированный доход основывается на прогнозах денежных потоков, подверженных рискам и формируемых в условиях неопределенности.
Формула чистого дисконтированного дохода дает понять, стоит ли вкладывать средства в определенный проект. При этом часто выбор происходит между различными планами при учете не только длительности жизненного цикла, но исроков вложения инвестиций, величины и характера поступающих доходов от соответствующего вида предпринимательской деятельности.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Чистый дисконтированный доход | это… Что такое Чистый дисконтированный доход?
Чистый дисконтированный доход
Чистая текущая стоимость (чистая приведённая стоимость) (англ. Net present value, принятое в международной практике анализа инвестиционных проектов сокращение — NPV (ЧДД)) — это сумма дисконтированных значений потока платежей, приведённых к сегодняшнему дню.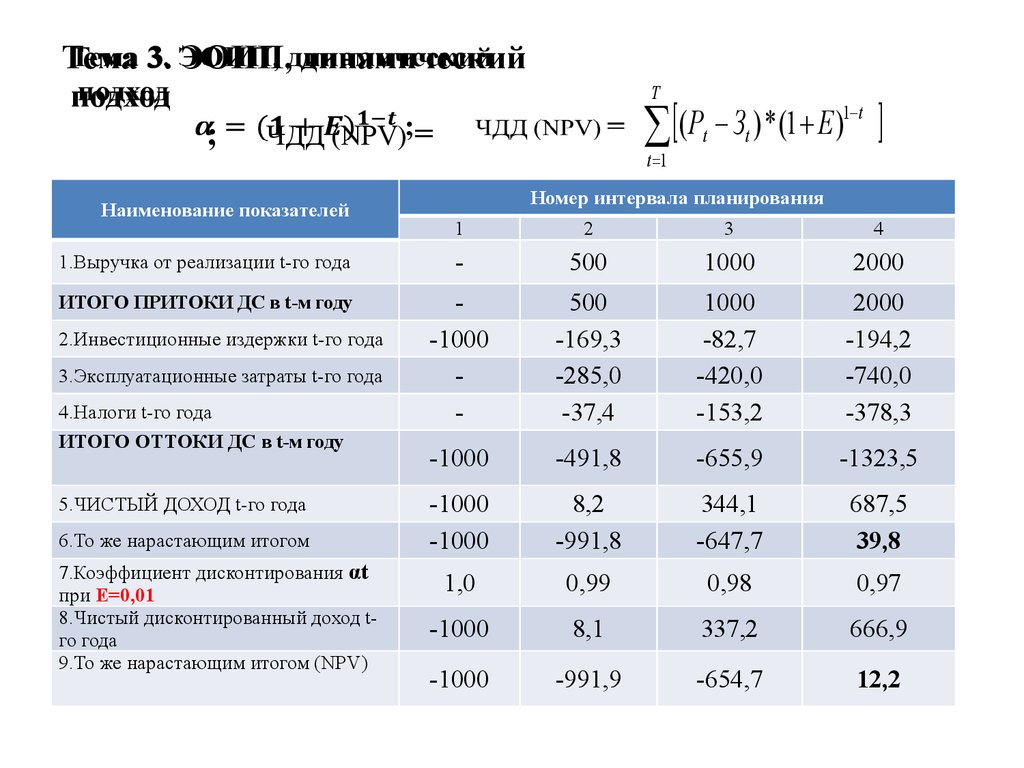 Показатель NPV представляет собой разницу между всеми денежными притоками и оттоками, приведенными к текущему моменту времени (моменту оценки инвестиционного проекта). Он показывает величину денежных средств, которую инвестор ожидает получить от проекта, после того, как денежные притоки окупят его первоначальные инвестиционные затраты и периодические денежные оттоки, связанные с осуществлением проекта. Поскольку денежные платежи оцениваются с учетом их временной стоимости и рисков, NPV можно интерпретировать, как стоимость, добавляемую проектом. Ее также можно интерпретировать как общую прибыль инвестора. В пользу такой интерпретации говорит то, что отношение NPV к совокупной величине дисконтированных инвестиционных затрат называется Индекс прибыльности (англ. Profitability Index или сокращенно PI).
Показатель NPV представляет собой разницу между всеми денежными притоками и оттоками, приведенными к текущему моменту времени (моменту оценки инвестиционного проекта). Он показывает величину денежных средств, которую инвестор ожидает получить от проекта, после того, как денежные притоки окупят его первоначальные инвестиционные затраты и периодические денежные оттоки, связанные с осуществлением проекта. Поскольку денежные платежи оцениваются с учетом их временной стоимости и рисков, NPV можно интерпретировать, как стоимость, добавляемую проектом. Ее также можно интерпретировать как общую прибыль инвестора. В пользу такой интерпретации говорит то, что отношение NPV к совокупной величине дисконтированных инвестиционных затрат называется Индекс прибыльности (англ. Profitability Index или сокращенно PI).
Иначе говоря, для потока платежей CF (Cash Flow), где CFt — платёж через t лет (t = 1,…,N) и начальной инвестиции IC (Invested Capital) в размере IC = − CF0 чистый дисконтированный доход NPV рассчитывается по формуле:
,
где i — ставка дисконтирования.
В обобщенном варианте, инвестиции также должны дисконтироваться, так как в реальных проектах они осуществляются не одномоментно (в нулевом периоде), а растягиваются на несколько периодов. Расчёт ЧДД — стандартный метод оценки эффективности инвестиционного проекта и показывает оценку эффекта от инвестиции, приведённую к настоящему моменту времени с учётом разной временно́й стоимости денег. Если ЧДД больше 0, то инвестиция экономически эффективна, а если ЧДД меньше 0, то инвестиция экономически невыгодна (т.е. альтернанивный проект, доходность которого принята в качестве ставки дисконтирования требует меньших инвестиций для получения аналогичного потока доходов).
С помощью ЧДД можно также оценивать сравнительную эффективность альтернативных вложений (при одинаковых начальных вложениях более выгоден проект с наибольшим ЧДД). Но все же для сравнительного анализа более применимыми являются относительные показатели. Применительно к анализу инвестиционных проектов таким показателем является Внутренняя норма доходности[1]
В отличие от показателя дисконтированной стоимости при расчете чистого дисконтированного дохода учитывается начальная инвестиция.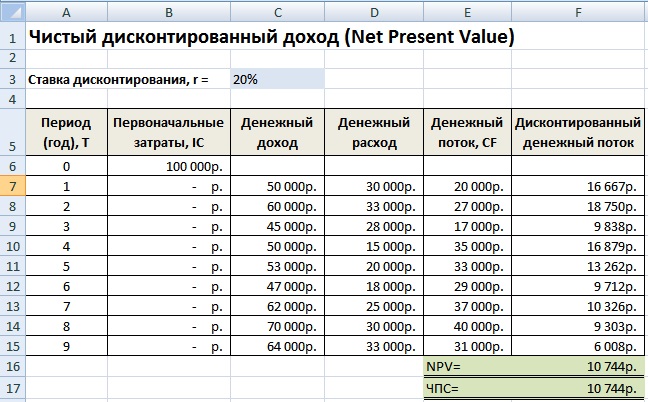
Содержание
|
Достоинства и недостатки
Положительные качества ЧДД:
- чёткие критерии принятия решений
- показатель учитывает стоимость денег во времени (используется коэффициент дисконтирования в формулах).
Отрицательные качества ЧДД:
- показатель не учитывает риски (да ладно? а я думал в ставке дисконтирования уже заложены риски. Ведь для более рискованных проектов ставка дисконтирования выше, для менее рискованных — ниже).
- Хотя все денежные потоки (коэффициент дисконтирования может включать в себя инфляцию, однако зачастую это всего лишь норма прибыли, которая закладывается в расчетный проект) являются прогнозными значениями, формула не учитывает вероятность исхода события (как это не учитывает вероятность исхода событий? ведь при подсчете будущих денежных потоков берутся ожидаемые потоки, следовательно все вероятности учитываются).

Пример
Машинный перевод:
Корпорация должна решить, следует ли вводить новые линейки продуктов. Новый продукт будет иметь расходы на запуск, эксплуатационные расходы, а также входящие денежные потоки в течение шести лет. Этот проект будет иметь немедленный (T = 0) отток денежных средств в размере 100000 (которые могут включать в себя механизмы, а также расходы обучение персонала). Другие оттоки денежных средств за 1-6 лет ожидаются в размере $ 5000 в год. Приток денежных средств, как ожидается, составит $ 30000 за каждый год 1-6. Все денежные потоки после уплаты налогов, и на 6 год ни каких денежных потоков не планируется. Необходимая норма прибыли составляет 10%. Приведенная стоимость (PV) может быть рассчитана по каждому году:
| Year | Cashflow | Present Value |
|---|---|---|
| T=0 | -$100,000 | |
| T=1 | $22,727 | |
| T=2 | $20,661 | |
| T=3 | $18,783 | |
| T=4 | $17,075 | |
| T=5 | $15,523 | |
| T=6 | $14,112 |
Сумма всех этих значений является настоящей чистой приведенной стоимостью, которая равна $ 8,881. 52. Поскольку NPV больше нуля, то было бы лучше инвестировать в проект, чем класть деньги в банк, и корпорации должны вкладывать средства в этот проект, если нет альтернативы с более высоким NPV.
52. Поскольку NPV больше нуля, то было бы лучше инвестировать в проект, чем класть деньги в банк, и корпорации должны вкладывать средства в этот проект, если нет альтернативы с более высоким NPV.
Тот же пример с формулами в Excel:
- NPV (ставка, net_inflow) + initial_investment
- PV (ставка, year_number, yearly_net_inflow)
При более реалистичных проблемах необходимо будет рассмотреть другие факторы, как расчет налогов, неравномерный денежный поток и ценности, а также наличие альтернативные возможности для инвестиций.
Кроме того, если мы будем использовать формулы упомянутых выше, для расчета NPV то мы видим, что приток денежных средств являются непрерывными и имеют такую же сумму формуле
can be used
= 4.36
Как уже упоминалось выше, что результат этой формулы, если, умноженная на годовой Чистые денежные средства, в-потоки и сократить на первоначальные затраты средств будет Чистая приведенная стоимость (NPV), так [4,36 * (30000 − 5000)] − 100000 = $8881,52 Поскольку NPV больше нуля, то было бы лучше инвестировать в проект, чем ничего не делать, и корпорации должны вкладывать средства в этот проект, если нет альтернативы с более высоким NPV.
См.также
- Стоимость денег с учётом фактора времени
- Дисконтированная стоимость
- Внутренняя норма доходности
- Срок окупаемости
- Индекс рентабельности
Ссылки
- Раздел «Показатели эффективности инвестиционных проектов: NPV» на сайте www.investplans.ru
- Виленский П. Л., Лившиц В. Н., Смоляк С. А. Оценка эффективности инвестиционных проектов. Теория и практика. — М.: Дело, 2008. — 1104 с. — ISBN 978-5-7749-0518-8.
- Четыркин Е. М. Финансовая математика. — М.: Дело, 2008. — 400 с. — ISBN 978-5-7749-0504-1.
Расчет чистой приведенной стоимости в Excel — формула чистой приведенной стоимости
В этом учебном пособии вы узнаете, как использовать функцию Excel чистой приведенной стоимости инвестиций и как избежать распространенных ошибок при расчете чистой приведенной стоимости в Excel.
Чистая приведенная стоимость или чистая приведенная стоимость является ключевым элементом финансового анализа, который показывает, будет ли проект прибыльным или нет. Почему чистая текущая стоимость так важна? Потому что основная финансовая концепция гласит, что деньги, которые потенциально могут быть получены в будущем, стоят меньше, чем та же сумма денег, которая у вас есть прямо сейчас. Чистая приведенная стоимость дисконтирует денежные потоки, ожидаемые в будущем, к настоящему, чтобы показать их сегодняшнюю стоимость.
Почему чистая текущая стоимость так важна? Потому что основная финансовая концепция гласит, что деньги, которые потенциально могут быть получены в будущем, стоят меньше, чем та же сумма денег, которая у вас есть прямо сейчас. Чистая приведенная стоимость дисконтирует денежные потоки, ожидаемые в будущем, к настоящему, чтобы показать их сегодняшнюю стоимость.
Microsoft Excel имеет специальную функцию для расчета чистой приведенной стоимости, но ее использование может быть сложным, особенно для людей, не имеющих большого опыта в области финансового моделирования. Цель этой статьи — показать вам, как работает функция Excel NPV, и указать на возможные подводные камни при расчете чистой приведенной стоимости ряда денежных потоков в Excel.
- Что такое чистая приведенная стоимость (NPV)?
- Функция Excel NPV
- Как рассчитать NPV в Excel – примеры формул
- PV по сравнению с NPV
- NPV по сравнению с XNPV
- Распространенные ошибки при расчете NPV в Excel
Что такое чистая приведенная стоимость (NPV)?
Чистая приведенная стоимость (NPV) представляет собой стоимость ряда денежных потоков за весь срок реализации проекта, дисконтированных до настоящего времени.
Проще говоря, NPV можно определить как приведенную стоимость будущих денежных потоков за вычетом первоначальных инвестиционных затрат:
NPV = PV будущих денежных потоков – первоначальные инвестиции
Чтобы лучше понять идею, давайте углубимся в математику.
Для одного денежного потока текущая стоимость (PV) рассчитывается по следующей формуле:
Где:
- r – дисконт или процентная ставка
- i – период движения денежных средств
Например, чтобы получить 110 долларов (будущая стоимость) через 1 год (i), какую сумму вы должны инвестировать сегодня на свой банковский счет с годовой процентной ставкой 10% (r)? Приведенная выше формула дает такой ответ: 91 = 100 долларов
Другими словами, 100 долларов — это текущая стоимость 110 долларов, которые, как ожидается, будут получены в будущем.
Чистая текущая стоимость (NPV) суммирует текущую стоимость всех будущих денежных потоков, чтобы привести их к единой точке в настоящем. И поскольку идея «чистого» показателя состоит в том, чтобы показать, насколько прибыльным будет проект после учета первоначальных капиталовложений, необходимых для его финансирования, сумма первоначальных инвестиций вычитается из суммы всех текущих стоимостей:
И поскольку идея «чистого» показателя состоит в том, чтобы показать, насколько прибыльным будет проект после учета первоначальных капиталовложений, необходимых для его финансирования, сумма первоначальных инвестиций вычитается из суммы всех текущих стоимостей:
Где:
- р – скидка или процентная ставка
- n – количество периодов времени
- i – период движения денежных средств
Поскольку любое ненулевое число, возведенное в нулевую степень, равно 1, мы можем включить в сумму первоначальные инвестиции. Обратите внимание, что в этой компактной версии формулы NPV i=0, т.е. первоначальные инвестиции сделаны в период 0.
Например, чтобы найти NPV для ряда денежных потоков (50, 60, 70) дисконтированных при 10% и начальной стоимости 100 долларов вы можете использовать эту формулу:
Или
Как чистая приведенная стоимость помогает в оценке финансовой жизнеспособности предлагаемых инвестиций? Предполагается, что инвестиции с положительной NPV будут прибыльными, а инвестиции с отрицательной NPV будут убыточными. Эта концепция лежит в основе правила Net Present Value Rule , в котором говорится, что вы должны участвовать только в проектах с положительной чистой приведенной стоимостью.
Эта концепция лежит в основе правила Net Present Value Rule , в котором говорится, что вы должны участвовать только в проектах с положительной чистой приведенной стоимостью.
Функция Excel NPV
Функция NPV в Excel возвращает чистую текущую стоимость инвестиций на основе дисконтной или процентной ставки и ряда будущих денежных потоков.
Синтаксис функции Excel NPV следующий:
NPV(ставка, значение1, [значение2], …)
Где:
- Ставка (обязательно) — скидка или процентная ставка за один период. Он должен быть указан в процентах или соответствующем десятичном числе.
- Значение1, [значение2], … — числовые значения, представляющие серию регулярных денежных потоков. Value1 является обязательным, последующие значения необязательны. В современных версиях Excel с 2007 по 2019 г., может быть предоставлено до 254 аргументов-значений; в Excel 2003 и старше – до 30 аргументов.
Функция NPV доступна в Excel 365 — 2000.
Советы:
- Чтобы рассчитать текущую стоимость аннуитета, используйте функцию Excel PV.
- Чтобы оценить прогнозируемый доход от инвестиций, выполните расчет внутренней нормы доходности.
4 вещи, которые вы должны знать о функции NPV
Чтобы убедиться, что ваша формула NPV вычисляется правильно, пожалуйста, имейте в виду следующие факты:
- Значения должны встречаться в конце каждого периода . Если первый денежный поток (первоначальные инвестиции) возникает в начале первого периода , используйте одну из этих формул NPV.
- Значения должны быть предоставлены в хронологическом порядке и через равные промежутки времени .
- Используйте отрицательных значений для представления оттоков (выплаченных денежных средств) и положительных значений для представления притоков (полученных денежных средств).
- Только 9Обрабатываются числовые значения 0007 .
 Пустые ячейки, текстовые представления чисел, логические значения и значения ошибок игнорируются.
Пустые ячейки, текстовые представления чисел, логические значения и значения ошибок игнорируются.
Как работает функция NPV в Excel
Использование функции NPV в Excel немного затруднительно из-за способа реализации этой функции. По умолчанию предполагается, что инвестиции сделаны за один период до даты value1 . По этой причине формула чистой приведенной стоимости работает правильно только в том случае, если вы указываете первоначальные инвестиционные затраты 9.A4
Эта формула переходит в ячейку C4, а затем копируется в ячейки ниже. Благодаря разумному использованию абсолютных и относительных ссылок на ячейки формула идеально подстраивается для каждой строки, как показано на снимке экрана ниже.
Обратите внимание, что мы также рассчитываем текущую стоимость первоначальных инвестиций, поскольку первоначальная стоимость инвестиций составляет через 1 год , поэтому она также дисконтируется.
После этого суммируем все текущие значения:
=СУММ(C4:C9)
А теперь вычислим NPV с помощью функции Excel:
=NPV(B1, B4:B9)
Как видите, результаты обоих расчетов точно совпадают:
Но что, если первоначальные затраты происходит в начале первого периода , как обычно?
Поскольку первоначальные инвестиции сделаны сегодня, к ним не применяется дисконтирование, и мы просто прибавляем эту сумму к сумме текущих стоимостей будущих денежных потоков (поскольку это отрицательное число, оно фактически вычитается):
=СУММ(C4:C9)+B4
И в этом случае ручной расчет и функция Excel NPV дают разные результаты:
Означает ли это, что мы не можем полагаться на формулу NPV в Excel и должны вычислять чистая текущая стоимость вручную в этой ситуации? Конечно нет! Вам просто нужно немного настроить функцию NPV, как описано в следующем разделе.
Как рассчитать NPV в Excel
Когда первоначальные инвестиции сделаны в начале первого периода , мы можем рассматривать его как денежный поток в конце предыдущего периода (т.е. периода 0). Имея это в виду, есть два простых способа найти NPV в Excel.
Формула NPV в Excel 1
Оставьте начальную стоимость вне диапазона значений и вычтите ее из результата функции NPV. Поскольку первоначальные затраты обычно вводятся как отрицательное число , вы фактически выполняете операцию сложения:
NPV(ставка, значения) + первоначальные затраты
В этом случае функция Excel NPV просто возвращает текущую стоимость неравномерных денежных средств. течет. Поскольку нам нужна «чистая» (т. е. приведенная стоимость будущих денежных потоков за вычетом первоначальных инвестиций), мы вычитаем первоначальные затраты вне функции NPV.
Формула чистой приведенной стоимости в Excel 2
Включите начальную стоимость в диапазон значений и умножьте результат на (1 + ставка).
В этом случае функция Excel NPV даст вам результат для периода -1 (как если бы первоначальные инвестиции были сделаны за один период до периода 0), мы должны умножить его выход на (1 + r), чтобы получить NPV переносится на один период вперед (т. е. от i = -1 до i = 0). См. компактную форму формулы NPV.
NPV(ставка, значения) * (1+ставка)
Выбор формулы зависит от ваших личных предпочтений. Я лично считаю, что первый проще и понятнее.
Калькулятор NPV в Excel
Теперь давайте посмотрим, как вы можете использовать приведенные выше формулы на реальных данных, чтобы сделать свой собственный калькулятор NPV в Excel.
Предположим, у вас есть первоначальные затраты в B2, ряд будущих денежных потоков в B3:B7 и требуемая доходность в F1. Чтобы найти NPV, используйте одну из следующих формул:
Формула NPV 1:
=NPV(F1, B3:B7) + B2
Обратите внимание, что первый аргумент значения — это денежный поток в периоде 1 (B3), первоначальная стоимость (B2) не включена.
NPV Формула 2:
=NPV(F1, B2:B7) * (1+F1)
Эта формула включает начальную стоимость (B2) в диапазоне значений.
На приведенном ниже снимке экрана показан наш калькулятор NPV в Excel в действии:
Чтобы убедиться, что наши формулы NPV в Excel верны, давайте проверим результат с помощью ручных вычислений. 9A3
Затем сложите все текущие значения и вычтите первоначальную стоимость инвестиций:
=СУММ(C3:C7)+B2
… и убедитесь, что результаты всех трех формул абсолютно одинаковы.
Примечание. В этом примере мы имеем дело с годовыми денежными потоками и годовой ставкой. Если вы хотите найти за квартал или за месяц NPV в Excel, не забудьте соответствующим образом скорректировать ставку дисконтирования, как описано в этом примере.
Разница между PV и NPV в Excel
В финансах как PV, так и NPV используются для измерения текущей стоимости будущих денежных потоков путем дисконтирования будущих сумм до настоящих. Но они отличаются одним важным моментом:
Но они отличаются одним важным моментом:
- Приведенная стоимость (PV) — относится ко всем будущим поступлениям денежных средств в данный период.
- Чистая приведенная стоимость (NPV) – разница между приведенной стоимостью притока денежных средств и приведенной стоимостью оттока денежных средств.
Другими словами, PV учитывает только приток денежных средств, в то время как NPV также учитывает первоначальные инвестиции или затраты, что делает его чистым показателем.
В Microsoft Excel есть два существенных различия между функциями:
- Функция NPV может рассчитывать неравномерные (переменные) денежные потоки. Функция PV требует, чтобы денежные потоки были постоянными в течение всего срока действия инвестиций.
- При использовании NPV денежные потоки должны возникать в конце каждого периода. PV может обрабатывать денежные потоки, возникающие в конце и в начале периода.
Разница между NPV и XNPV в Excel
XNPV — еще одна финансовая функция Excel, которая вычисляет чистую приведенную стоимость инвестиций. Основное различие между функциями заключается в следующем:
Основное различие между функциями заключается в следующем:
- NPV считает, что все периоды времени равны .
- XNPV позволяет указать даты, соответствующие каждому денежному потоку. По этой причине функция XNPV намного более точна при работе с рядом денежных потоков через нерегулярных интервалов 9.0008 .
В отличие от NPV, функция Excel XNPV реализована «нормально» — первое значение соответствует оттоку, который происходит в начале инвестиции. Все последующие денежные потоки дисконтируются на основе 365-дневного года.
С точки зрения синтаксиса функция XNPV имеет один дополнительный аргумент:
XNPV(ставка, значения, даты)
В качестве примера, давайте используем обе функции на одном и том же наборе данных, где F1 — ставка дисконтирования, B2: B7 — денежные потоки, а C2:C7 — даты:
= NPV(F1,B3:B7)+B2
=XNPV(F1,B2:B7,C2:C7)
Функции NPV и XNPV возвращают очень близкие значения:
В случае нерегулярных интервалов разница между результатами очень значительна:
Распространенные ошибки при расчете NPV в Excel
Из-за весьма специфической реализации NPV функции, при расчете чистой приведенной стоимости в Excel делается много ошибок. На простых примерах ниже показаны наиболее типичные ошибки и способы их избежать.
На простых примерах ниже показаны наиболее типичные ошибки и способы их избежать.
Неравномерные интервалы
Функция Excel NPV предполагает, что все периоды денежных потоков равны . Если вы укажете разные интервалы, скажем, годы и кварталы или месяцы, чистая приведенная стоимость будет неверной из-за несогласованных периодов времени.
Пропущенные периоды или денежные потоки
NPV в Excel не распознает пропущенные периоды и игнорирует пустые ячейки. Чтобы правильно рассчитать NPV, обязательно укажите последовательных месяцев, кварталов или лет и укажите ноль значения для периодов времени с нулевыми денежными потоками.
Ставка дисконтирования не соответствует фактическим периодам времени
Функция Excel NPV не может автоматически приспосабливать указанную ставку к заданным временным частотам, например годовую ставку дисконтирования к ежемесячным денежным потокам. Пользователь несет ответственность за предоставление соответствующей ставки за период .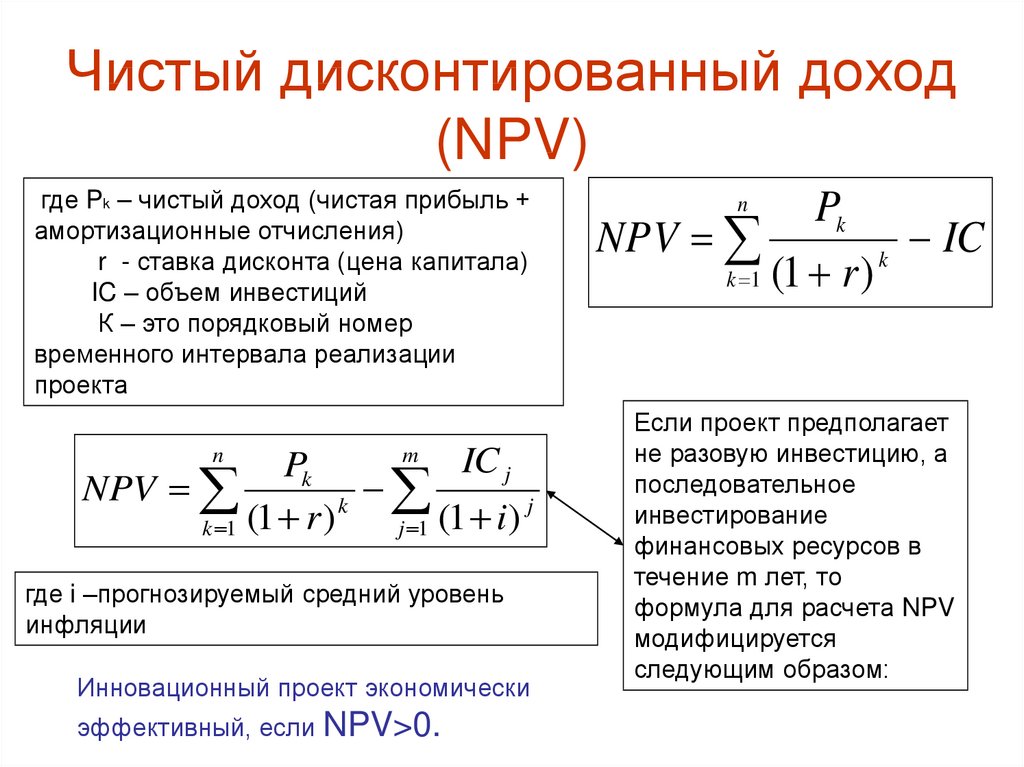
Неверный формат курса
Скидка или процентная ставка должны быть указаны как процент или соответствующее десятичное число . Например, 10-процентная ставка может быть указана как 10% или 0,1. Если вы введете ставку как число 10, Excel примет ее за 1000%, и чистая приведенная стоимость будет рассчитана неправильно.
Вот как можно использовать NPV в Excel, чтобы найти чистую текущую стоимость инвестиций. Чтобы более подробно ознакомиться с формулами, обсуждаемыми в этом руководстве, загрузите наш образец калькулятора чистой приведенной стоимости для Excel.
Спасибо за внимание и надеемся увидеть вас в нашем блоге на следующей неделе!
Вас также может заинтересовать
Чистая приведенная стоимость (NPV) – Значение, формула, расчеты
Чистая приведенная стоимость (NPV), чаще всего текущая стоимость притока денежных средств и текущая стоимость оттока денежных средств за период времени проекта.
Если разница положительная, то это прибыльный проект, а если отрицательная, то не достойный.
Содержание
- Чистая приведенная стоимость (NPV) Определение
- Формула чистой приведенной стоимости (NPV)
- Объяснение формулы чистой приведенной стоимости Калькулятор
- Чистая приведенная стоимость в Excel (с шаблоном Excel)
- NPV Video
- Рекомендуемые статьи:
Формула чистой приведенной стоимости (NPV)
NPV t=1 to T = ∑X t / [(1+R) t – X 0 ]
Вы можете использовать эти изображения на своем веб-сайте и т. д. ., Пожалуйста, предоставьте нам ссылку на атрибуциюКак предоставить атрибуцию?Ссылка на статью должна быть гиперссылкой
Например:
Источник: Чистая приведенная стоимость (NPV) (wallstreetmojo.com)
Вот формула чистой приведенной стоимости (когда денежные поступления четный):
NPV t=1 to T = ∑ X T /(1 + R) T — x O
, где,
- x T = общее количество денежных инвестиций для периода T
- x O = NET Investenture.
 ставка дисконтирования, наконец,
ставка дисконтирования, наконец, - t = общее количество периодов времени
Формула чистой приведенной стоимости (при неравномерном поступлении денежных средств): i2 /(1+r) 2 + C i3 /(1+r) 3 + …] – X o
Где,
- R – указанная норма доходности за период;
- C i1 — консолидированное поступление денежных средств за первый период;
- C i2 — консолидированное поступление денежных средств за второй период;
- C i3 – консолидированное поступление денежных средств в течение третьего периода и т. д.
Объяснение формулы чистой приведенной стоимости
Формула NPV состоит из двух частей. 9n, где PV = текущая стоимость, FV = будущая стоимость, I = проценты (стоимость капитала) и n = количество лет], чтобы дисконтировать будущую стоимость и выяснить приток денежных средств от инвестиций на текущую дату.
Если стоимость инвестиций меньше денежных поступлений от инвестиций, то проект вполне хорош для инвестора, так как он получает больше, чем платит. В противном случае, если стоимость инвестиций больше денежных поступлений от инвестиций, то лучше отказаться от проекта, так как инвестор должен заплатить больше, чем он платит на данный момент.
Примеры
Вы можете скачать этот шаблон Excel с чистой приведенной стоимостью здесь – Шаблон Excel с чистой приведенной стоимостью
Hills Ltd. хотела бы инвестировать в новый проект. У компании есть следующая информация об этой новой инвестиции —
- Стоимость новой инвестиции на данный момент — 265 000 долларов США
- Проект получит приток денежных средств следующим образом —
- Год 1 – 60 000 долларов США
- Год 2 – 70 000 долларов США 95
- Шаг 1 заключается в применении формулы чистой приведенной стоимости для расчета приведенной стоимости явного периода FCFF.
- Шаг 2 заключается в применении формулы чистой приведенной стоимости для расчета PV конечной стоимости.
- Во-первых, это очень легко вычислить. Прежде чем принимать какие-либо решения относительно инвестиций, если вы знаете, как рассчитать NPV, вы сможете принимать более обоснованные решения.
- Во-вторых, он сравнивает текущую стоимость притока и оттока денежных средств.
 В результате сравнение дает инвесторам правильную перспективу для принятия правильного решения.
В результате сравнение дает инвесторам правильную перспективу для принятия правильного решения. - В-третьих, NPV предлагает вам окончательное решение. Рассчитав это, вы сразу узнаете, стоит ли идти на инвестиции или нет.
- Формула значения в ExcelФормула значения В ExcelIn Excel функция значения возвращает значение текста, представляющего число.

= 54 545,5 + 57,851,2 + 60,105,2 + 61 471,2 + 62 092,1 = 296 065,2
Чистая приведенная стоимость = инвестирование денежных средств из инвестиций — стоимость инвестиций
или, чистая стоимость = 296 06,06555555 год.
 можете быть уверены, что это достойная инвестиция; потому что чистая приведенная стоимость этих новых инвестиций положительна.
можете быть уверены, что это достойная инвестиция; потому что чистая приведенная стоимость этих новых инвестиций положительна.Использование чистой приведенной стоимости для оценки — пример использования Alibaba
В марте 2019 года Alibaba получит свободный денежный поток в размере 1,2 миллиарда долларов.. Как мы отмечаем ниже, Alibaba будет генерировать предсказуемый положительный свободный денежный поток Денежные потоки Денежный поток в фирму или капитал после погашения всех долгов и обязательств называется свободным денежным потоком (FCF). Он измеряет, сколько денежных средств зарабатывает фирма после вычета необходимого оборотного капитала и капитальных затрат (CAPEX). подробнее.
Общая сумма расчетов чистой приведенной стоимости на шагах 1 и 2 дает нам общую стоимость предприятия Alibaba.

Ниже приведена таблица, в которой обобщается DCF-оценка Alibaba. DCF-оценкаАнализ дисконтированных денежных потоков — это метод анализа приведенной стоимости компании, инвестиций или денежных потоков путем корректировки будущих денежных потоков с учетом временной стоимости денег. Этот анализ оценивает текущую справедливую стоимость активов, проектов или компаний, принимая во внимание многие факторы, такие как инфляция, риск и стоимость капитала, а также анализируя будущие результаты деятельности компании.Подробнее.
Использование и релевантность
Используя эту формулу, инвесторы находят разницу между притоком денежных средств от инвестиций и стоимостью инвестиций.
Используется для принятия взвешенных деловых решений по следующим причинам –
Вы можете использовать следующий калькулятор чистой приведенной стоимости
Года1 Год 2 Год 3 Год года .0613 R (percentage) Cash Inflows from Investments Cost of Investments Net Present Value Formula =
Чистая приведенная стоимость в Excel (с шаблоном Excel)Net Present Value Формула = [Год1/(1 + R) 1 + Год2/(1 + R) 2 + Год3/(1 + R) 3 + Год4/(1 + R) 4 + Год5/(1 + Р) 5 ] − Стоимость инвестиций = [0/(1+0) 1 + 0/(1+0) 2 + 4 0/(1+03) +0) 4 + 0/(1+0) 5 ] − 0 = 0 Теперь давайте сделаем тот же пример выше в Excel.

Это очень просто. Вам необходимо предоставить два входа: приток денежных средств от инвестиций и стоимость инвестиций.
Вы можете легко рассчитать NPV в ExcelNPV В Excel NPV (чистая текущая стоимость) инвестиции рассчитывается как разница между текущим притоком и оттоком денежных средств. Это функция Excel и финансовая формула, которая принимает значение скорости для притока и оттока в качестве входных данных. Подробнее см. предоставленный шаблон.
Шаг 1 – Найдите текущую стоимость притока денежных средств.
Шаг 2 – Найдите сумму текущих значений.
Этап 3. Расчет чистой приведенной стоимости = 296 065,2 долл. США – 265 000 долл. США = 31 065,2 долл. США. Здесь мы обсудим формулу для расчета чистой приведенной стоимости, а также примеры, интерпретацию и использование. Вы также можете ознакомиться с этими статьями ниже, чтобы узнать больше о финансовом анализе –

 Пустые ячейки, текстовые представления чисел, логические значения и значения ошибок игнорируются.
Пустые ячейки, текстовые представления чисел, логические значения и значения ошибок игнорируются. Если разница положительная, то это прибыльный проект, а если отрицательная, то не достойный.
Если разница положительная, то это прибыльный проект, а если отрицательная, то не достойный. ставка дисконтирования, наконец,
ставка дисконтирования, наконец, можете быть уверены, что это достойная инвестиция; потому что чистая приведенная стоимость этих новых инвестиций положительна.
можете быть уверены, что это достойная инвестиция; потому что чистая приведенная стоимость этих новых инвестиций положительна.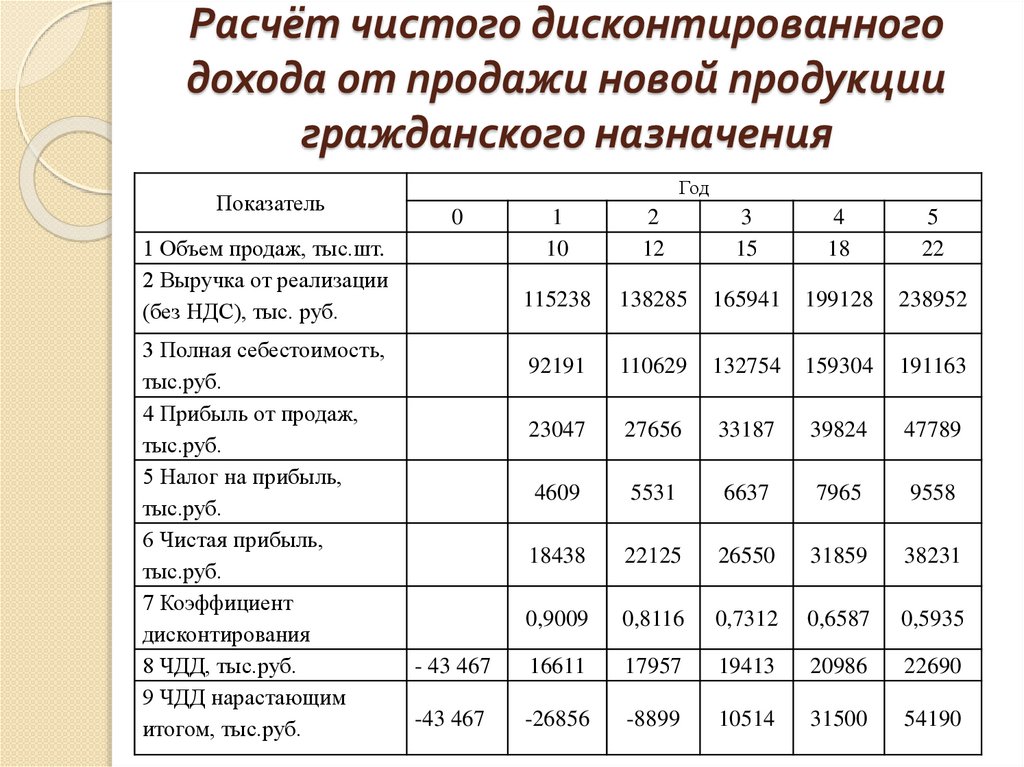
 В результате сравнение дает инвесторам правильную перспективу для принятия правильного решения.
В результате сравнение дает инвесторам правильную перспективу для принятия правильного решения.
Об авторе