Как рассчитать pv – Pv что это такое и как рассчитать, расчет нпв
Что такое и как рассчитать показатель PV
У многих, кто так или иначе связан с расчетом инвестиций, рано или поздно возникает вопрос: PV – что это такое, и как рассчитать? На самом деле здесь нет ничего сложного, и справиться с такими расчетами может любой желающий.

Прежде всего, PV – это дисконтированная стоимость будущей суммы. Однако, не стоит удивляться, когда вы слышите другие названия: также некоторые её называют текущей или приведенной стоимостью.
Допустим, у нас есть некоторая сумма денег PV, вкладываемая c фиксированной ставкой i в временную единицу t. В качестве временной единицы у нас может выступать что угодно: день и даже год.
То есть, получается, что за каждую временную единицу t зачисляются сверху проценты. Следовательно, в будущем, характеризующимся моментом t. у нас получается сумма FVt, рассчитываемая следующим образом:
FV
t=РV(1+i)t
Отсюда можно вывести показатель текущей стоимости РV. Порядок её расчета таков:
РV=FVt(1+i)-t=FVt/(1+i)t
Тогда выходит, что PV – дисконтированная стоимость суммы FVt в будущем, а i – ставка дисконтирования. Такая операция нахождения PV называется дисконтированием.
В итоге, она может быть привязана не только к текущему времени, но и к абсолютно любому моменту времени. Для этого необходимо в знаменателе от индекса t отнять t0.
Предполагается, что есть возможность инвестировать сумму денег в абсолютно любые временные рамки. Например, мы вкладываемся в депозитный счет с показателем доходности i. Однако, при подобном расчете имеет смысл только доход при расчетах риска.
kak1000.ru
Финансовый анализ и инвестиционная оценка предприятия
Оба понятия из заголовка этого раздела, дисконтированная (приведенная) стоимость, ПС (presentvalue, или PV), и чистая дисконтированная (приведенная) стоимость, ЧПС (netpresentvalue, или NPV), обозначают текущую стоимость ожидаемых в будущем денежных поступлений.
В качестве примера рассмотрим оценку инвестиции, обещающей доход 100 долл. в год в конце нынешнего и еще четырех следующих лет. Предполагаем, что эта серия из пяти платежей по 100 долл. каждый гарантирована и деньги непременно поступят. Если бы банк платил нам годовой процент в размере 10% при депозите на пять лет, то эти десять процентов как раз и составляли бы альтернативную стоимость инвестиции — эталонную норму прибыли, с которой мы сравнивали бы выгоду от нашего вложения.
Можно вычислить ценность инвестиции путем дисконтирования денежных поступлений от нее с использованием альтернативной стоимости в качестве ставки дисконтирования.
Формула расчета в Excel дисконтированной (приведенной) стоимости (PV) = ЧПС(C1;B5:B9)
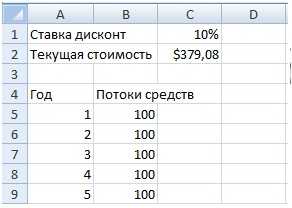
Приведенная стоимость (ПС) в объеме 379,08 долл. и есть текущая стоимость инвестиции.
Предположим, что данная инвестиция продавалась бы за 400 долл. Очевидно, она не стоила бы запрашиваемой цены, поскольку — при условии альтернативного дохода (учетной ставки) в размере 10% — реальная стоимость этого капиталовложения составляла бы только 379,08 долл. Здесь как раз уместно ввести понятие чистой приведенной стоимости (ЧПС). Обозначая символом r учетную ставку для данной инвестиции, получаем следующую формулу NPV:
Где СFt – денежное поступление от инвестиции в момент t; CF0 –поток средств (поступление) на текущий момент.
Формула расчета в Excel чистой дисконтированной (приведенной) стоимости (NPV) = ЧПС(C1;B6:B10)+B5
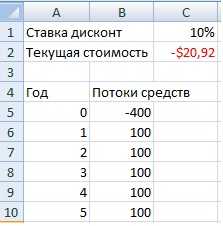
Терминология Excel, касающаяся дисконтируемых потоков денежных средств, несколько отличается от стандартной финансовой терминологии. В Excel сокращение МУР (ЧПС) обозначает приведенную стоимость (а не чистую приведенную стоимость) серии денежных поступлений.
Чтобы рассчитать в Excel чистую приведенную стоимость серии денежных поступлений в обычном понимании финансовой теории, необходимо сначала вычислить приведенную стоимость будущих денежных поступлений (с использованием такой функции Excel, как «ЧПС»), а затем вычесть из этого числа денежный поток на начальный момент времени. (Эта величина часто совпадает со стоимостью рассматриваемого актива.)
Автор: к.э.н. Жданов И.Ю.
Сайт: www.beintrend.ru
beintrend.ru
NPV формула расчета пример. NPV инвестиционного проекта
Инвестировать — это значит вложить свободные финансовые ресурсы сегодня с целью получения стабильных денежных потоков в будущем. Вкладываться можно в финансовые инструменты, или в новый бизнес, или в расширение уже существующего бизнеса. В любом случае, инвестирование — это вложение денег в какие-то активы на долгосрочную перспективу.
Как не ошибиться и не только вернуть вложенные средства, но еще и получить прибыль от инвестиций?
Для этого можно воспользоваться одним из методов оценки эффективности инвестиционных проектов. NPV — это один из таких методов. Найти NPV инвестиционного проекта означает найти чистую приведенную стоимость всех денежных потоков, связанных с этим проектом.
Как это сделать, используя формулу для расчета NPV, и так ли это сложно, читайте ниже.
Что можно делать с деньгами?
Если у вас появилась некоторая сумма денег, то есть три возможности ими распорядиться:
- а) потратить — купить большую квартиру и жить в ней, купить автомобиль и ездить на нем на работу, съездить в отпуск на Гавайи. У каждого есть свои варианты, ведь, чтобы потратить деньги, советчики не нужны.
- б) спрятать в сейф на «черный день». И всё время трястись, что их украдут. И с грустью наблюдать, как они обесцениваются в результате инфляции
- в) «вложить» (инвестировать) куда-нибудь с целью получения дохода в будущем. А будет ли это выгодно?
Эта статья для тех, кто выбирает третий пункт из этого списка. И не важно, собираетесь ли вы инвестировать свои деньги или деньги компании, в которой вы будете работать финансовым специалистом.

Инвестировать можно в банк, положив деньги на депозит, а можно купить долговые обязательства или акции банков или компаний, которые свободно торгуются на финансовом рынке. Это самый простой путь, но не самый доходный. Для физических лиц, то есть нас с вами, чаще всего, это единственный способ вложения накоплений.
А можно инвестировать в бизнес, что означает купить долгосрочные активы (основные средства), используя которые в процессе производства, торговли или оказания услуг, вы будете получать в будущем притоки денежных средств. Для юридических лиц (компаний) это собственно говоря, и является целью их существования — делать деньги (прибыль) из инвестиций.
Чтобы определить, будет ли успешным тот или иной инвестиционный проект, финансовыми специалистами используются определенные методы оценки проектов. Два основных метода — это NPV и IRR.
NPV — что это такое? Какая логика в этом показателе?
NPV — это сокращение по первым буквам фразы «Net Present Value» и расшифровывается это как чистая приведенная (к сегодняшнему дню) стоимость. Это метод оценки инвестиционных проектов, основанный на методологии дисконтирования денежных потоков.
Если вы знаете перспективный бизнес-проект и хотите вложить в него деньги, то неплохо было бы для начала рассчитать NPV (=чистую приведенную стоимость) этого бизнес-проекта. Алгоритм расчета такой:
- 1) нужно оценить денежные потоки от проекта — первоначальное вложение (отток) денежных средств и ожидаемые поступления (притоки) денежных средств в будущем
- 2) определить стоимость капитала (cost of capital) для вас — это будет ставкой дисконтирования
- 3) продисконтировать все денежные потоки (притоки и оттоки) от проекта по ставке, которую вы оценили в п.2)
- 4) Сложить. Сумма всех дисконтированных потоков и будет равна NPV проекта
Правило: если NPV больше нуля, то проект можно принять, если NPV меньше нуля, то проект стоит отвергнуть.
Логическое обоснование метода NPV очень простое. Если NPV равно нулю, это означает, что денежные потоки от проекта достаточны, чтобы
- а) возместить инвестированный капитал и
- б) обеспечить необходимый доход на этот капитал.
Если NPV положительный, значит, проект принесет прибыль, и чем больше величина NPV, тем выгоднее/прибыльнее является данный проект. Поскольку доход кредиторов (у кого вы брали деньги в долг) фиксирован, весь доход выше этого уровня принадлежит акционерам. Если компания одобрит проект с нулевым NPV, позиция акционеров останется неизменной – компания станет больше, но цена акции не вырастет. Однако, если проект имеет положительную NPV, акционеры станут богаче.
Формула NPV — пример расчета
Формула расчета NPV выглядит сложно на взгляд человека, не относящего себя к математикам:
Где:
- n, t — количество временных периодов,
- CF — денежный поток (Cash Flow),
- R — стоимость капитала (ставка дисконтирования, Rate)
На самом деле эта формула — всего лишь правильное математическое представление суммирования нескольких величин. Чтобы рассчитать NPV, возьмем для примера два проекта А и Б, которые имеют следующую структуру денежных потоков в ближайшие 4 года:
Оба проекта А и Б имеют одинаковые первоначальные инвестиции в 10,000, но денежные потоки в последующие годы сильно разнятся. Проект А предполагает более быструю отдачу от инвестиций, но к четвертому году денежные поступления от проекта сильно упадут. Проект Б, напротив, в первые два года показывает более низкие денежные притоки, чем поступления от Проекта А, но зато в последующие два года Проект Б принесет больше денежных средств, чем проект А.
Рассчитаем NPV инвестиционного проекта следующим образом:
Предположения для упрощения расчета:
- а) все денежные потоки случаются в конце каждого года,
- б) первоначальный денежный отток (вложение денег) произошел в момент времени «ноль», т.е. сейчас
- б) стоимость капитала (ставка дисконтирования) составляет 10%
Про дисконтирование денежных потоков на этом сайте есть отдельная статья. Если расчет, приведенный ниже, вам покажется совсем непонятным, то лучше будет сначала вспомнить основы дисконтирования, вернувшись к этой статье.
Коротко напомню: чтобы привести денежный поток к сегодняшнему дню, нужно умножить денежную сумму на коэффициент 1/(1+R), при этом (1+R) надо возвести в степень, равную количеству лет. Величина этой дроби называется фактором или коэффициентом дисконтирования. Чтобы не вычислять каждый раз этот коэффициент, его можно посмотреть в специальной таблице, которая называется «таблица коэффициентов дисконтирования».
Применим формулу NPV для Проекта А. У нас четыре годовых периода и пять денежных потоков. Первый поток (10,000) — это наша инвестиция в момент времени «ноль», то есть сегодня. Если развернуть формулу NPV, приведенную чуть выше, то мы получим сумму из пяти слагаемых:
Если подставить в эту сумму данные из таблицы для Проекта А вместо CF и ставку 10% вместо R, то получим следующее выражение:
То, что стоит в делителе, можно рассчитать, но проще взять готовое значение из таблицы коэффициентов дисконтирования и умножить эти коэффициенты на сумму денежного потока.
В результате приведенная стоимость денежных потоков (NPV) для проекта А равна 788,2 доллара. Расчет NPV для проекта А можно так же представить в виде таблицы и в виде шкалы времени:
 Точно таким же образом рассчитывается NPV для проекта Б.
Точно таким же образом рассчитывается NPV для проекта Б.
Поскольку коэффициенты дисконтирования уменьшаются с течением времени, вклад в приведенную стоимость проекта больших (4,000 и 6,000), но отдалённых по времени (третий и четвертый годы) денежных потоков будет меньше, чем вклад от денежных поступлений в первые годы проекта. Поэтому ожидаемо, что для проекта Б чистая приведенная стоимость денежных потоков будет меньше, чем для Проекта А.
У меня получилось, что NPV Проекта Б — 491,5 доллара.
Расчет NPV для проекта Б можно посмотреть в таблице и на рисунке со шкалой времени.
 Вывод: оба проекта можно принять, так как NPV обоих проектов больше нуля, а, значит, осуществление этих проектов приведет к увеличению стоимости компании-инвестора.
Вывод: оба проекта можно принять, так как NPV обоих проектов больше нуля, а, значит, осуществление этих проектов приведет к увеличению стоимости компании-инвестора.
Если эти проекты взаимоисключающие, то есть необходимо выбрать один из них, то предпочтительнее выглядит Проект А, поскольку его NPV заметно больше 788,2, чем NPV Проекта Б 491,5.
Цифры для расчета NPV инвестиционного проекта — в чём сложность?
Применить математическую формулу несложно, если известны все переменные. Когда у вас есть все цифры — денежные потоки и стоимость капитала — то вы легко сможете подставить их в формулу и рассчитать NPV. Но не всё так просто. Реальная жизнь отличается от чистой математики тем, что невозможно точно определить величину переменных, которые входят в эту формулу. Собственно говоря, именно поэтому на практике примеров неудачных инвестиционных решений гораздо больше, чем удачных.
а) Денежные потоки
Самый важный и самый трудный шаг в анализе инвестиционных проектов — это оценка всех денежных потоков, связанных с проектом. Во-первых, это величина первоначальной инвестиции (оттока средств) сегодня. Во-вторых, это величины годовых притоков и оттоков денежных средств, которые ожидаются в последующие периоды.
Сделать точный прогноз всех расходов и доходов, связанных с большим комплексным проектом, невероятно трудно. Например, если инвестиционный проект связан с выпуском на рынок нового товара, то для расчета NPV необходимо будет сделать прогноз будущих продаж товара в штуках, и оценить цену продажи за единицу товара. Эти прогнозы основываются на оценке общего состояния экономики, эластичности спроса (зависимости уровня спроса от цены товара), потенциального эффекта от рекламы, предпочтений потребителей, а также реакции конкурентов на выход нового продукта.
Кроме того, необходимо будет сделать прогноз операционных расходов (платежей), а для этого оценить будущие цены на сырье, зарплату работников, коммунальные услуги, изменения ставок аренды, тенденции в изменении курсов валют, если какое-то сырье можно приобрести только за границей и так далее. И все эти оценки нужно сделать на несколько лет вперед.
б) Ставка дисконтирования
Ставка дисконтирования в формуле расчета NPV — это стоимость капитала (cost of capital) для инвестора. Другими словами, это ставка процента, по которой компания-инвестор может привлечь финансовые ресурсы.
В общем случае компания может получить финансирование из трех источников:
- взять в долг (обычно у банка)
- продать свои акции
- использовать внутренние ресурсы (нераспределенную прибыль)
ЧИТАЙТЕ ТАКЖЕ: Ставка дисконтирования для инвестиционного проекта. Это WACC — средневзвешенная стоимость капитала
Финансовые ресурсы, которые могут быть получены из этих трех источников, имеют свою стоимость. И она разная! Наиболее понятна стоимость долговых обязательств (пункт 1 списка). Это либо процент по долгосрочным кредитам, который требуют банки, либо процент по долгосрочным облигациям, если компания может выпустить свои долговые инструменты на финансовом рынке. Оценить стоимость финансирования из двух остальных источников сложнее. Финансистами давно разработаны несколько моделей для такой оценки, среди них небезызвестный CAPM (Capital Asset Pricing Model). Но есть и другие подходы.
Стоимость капитала для компании (и, следовательно, ставка дисконтирования в формуле NPV) будет средневзвешенная величина процентных ставок их этих трех источников. В англоязычной финансовой литературе это обозначается как WACC — сокращение по первым буквам английской фразы Weighted Average Cost of Capital, что переводится как средневзвешенная стоимость капитала.
Зависимость NPV проекта от ставки дисконтирования
Понятно, что получить абсолютно точные величины всех денежных потоков проекта и точно определить стоимость капитала, т.е. ставку дисконтирования невозможно. В этой связи интересно проанализировать зависимость NPV от этих величин. У каждого проекта она будет разная. Наиболее часто делается анализ чувствительности показателя NPV от стоимости капитала.
Давайте рассчитаем NPV по проектам А и Б для разных ставок дисконтирования. Я сделала этот расчет в Excele, результаты приведены в таблице ниже:
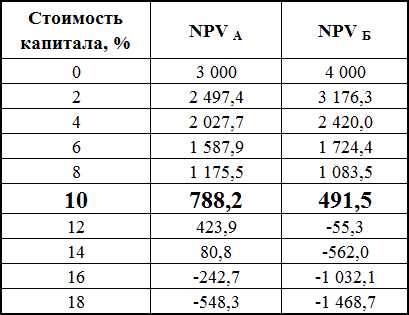
Табличная форма уступает графической по информативности, поэтому гораздо интереснее посмотреть результаты на графике (нажать, чтобы увеличить изображение):
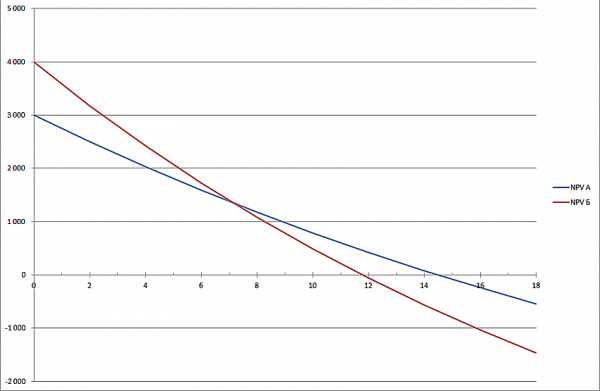
Из графика видно, что NPV проекта А превышает NPV проекта Б при ставке дисконтирования более 7% (точнее 7,2%). Это означает, что ошибка в оценке стоимости капитала для компании-инвестора может привести к ошибочному решению в плане того, какой проект из двух следует выбрать.
Кроме того, из графика также видно, что Проект Б (красная линия) является более чувствительным в отношении ставки дисконтирования. То есть NPV проекта Б уменьшается ,быстрее по мере роста этой ставки (красный график более крутой). И это легко объяснимо. В проекте Б денежные поступления в первые годы проекта невелики, со временем они увеличиваются. Но коэффициенты дисконтирования для более отдаленных периодов времени уменьшаются очень значительно. Поэтому вклад больших денежных потоков в чистую приведенную стоимость так же резко падает.
Например, можно рассчитать, чему будут равны 10,000 долларов через 1 год, 4 года и 10 лет при ставках дисконтирования 5% и 10%, то наглядно можно увидеть, как сильно зависит приведенная стоимость денежного потока от времени его возникновения:
В последнем столбце таблицы видно, что один и тот же денежный поток (10,000) при разных ставках дисконтирования отличается через год всего на 4.5%. Тогда как тот же самый по величине денежный поток, только через 10 лет от сегодняшнего дня при дисконтировании по ставке 10% будет на 37,2% меньше, чем его же приведенная стоимость при ставке дисконтирования 5%. Высокая стоимость капитала (=ставка дисконтирования) «съедает» существенную часть дохода от инвестиционного проекта в отдаленные годовые периоды, и с этим ничего не поделать. Это математика.
Именно поэтому, при оценке инвестиционных проектов денежные потоки, отстоящие от сегодняшнего дня более, чем на 10 лет, обычно не используются. Помимо существенного влияния дисконтирования, еще и точность оценки отдаленных по времени денежных потоков существенно ниже.
История с выбором между двумя проектами А и Б будет продолжена в следующих публикациях на тему методов оценки инвестиционных проектов. К сожалению, большинство статей в Интернете на эту тему написано сухо и коротко, и многие из публикаций содержат ошибки, что недопустимо.
Расчет NPV — пример в Excel
В нашем компьютерном веке стало гораздо проще делать любые расчеты. В программе Excel есть функция, с помощью которой расчет NPV можно сделать быстрее, чем по таблицам. И не нужно дисконтировать каждый поток вручную. Проще зайти в раздел Excel Формулы —> Финансовые и выбрать функцию ЧПС.
Пример расчета NPV для проекта А показан ниже:
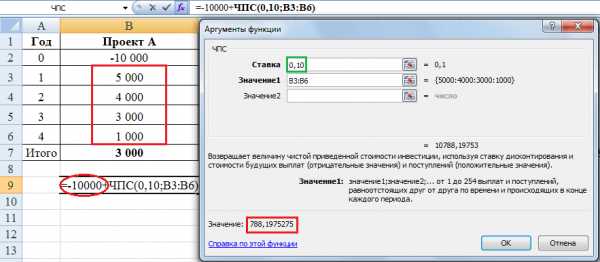
Единственная сложность заключается в том, что эта функция дисконтирует все потоки, которые вы выберете. Если же первый поток, как в проектах А и Б рассмотренных выше, приходится на период времени ноль, то его не надо вводить в ячейку значения. Первоначальная инвестиция в сумме -10,000 нужно добавить к тому значению, которое рассчитает функцию ЧПС. В этом примере дисконтируются ячейки B3-B6 (обведено красным в таблице), по ставке 0,10 (зеленый квадратик), приведенная стоимость получается равной 10,788.2. Если вычесть из этой суммы инвестицию 10,000, то получится NPV, равная 788,2. При расчете вручную мы получили 788,4, разница 0,2 получилась в результате округлений.
Другая функция программы Excel, расположенная в том же разделе финансовых формул, ЧИСТНЗ тоже считает приведенную стоимость денежных потоков, но она может это делать для неравных промежутков времени между потоками. В ней есть дополнительная ячейка, куда можно ввести диапазон дат, соответствующих времени поступления денежных средств.
И будет вам счастье и приличный счёт в банке.
Финансовая грамотность необходима каждому человеку. Современная экономика — это сложный механизм перекачивания денег из одного кармана в другой. И нужно не только научиться зарабатывать деньги, но и вкладывать их.
Учиться быть инвесторами желательно еще до того, как у вас появятся деньги. Если в будущем вам повезет, и вы выиграете миллион долларов в лотерею, то вы должны быть готовы к этому. Если вам удастся заработать достаточные для инвестирования средства, то тем более захочется распорядиться ими так, чтобы приумножить.
Другие статьи на этом сайте из рубрики «Финансы»:
Вернуться на главную страницу
msfo-dipifr.ru
CFA — Как рассчитывать текущую (приведенную) стоимость денежного потока (PV)? | программа CFA
Фактор будущей стоимости связывает сегодняшнюю текущую (приведенную) стоимость (PV, англ. ‘present value’) денежного потока с его будущей стоимостью (FV, англ. ‘future value’). Этот коэффициент позволяет рассчитать как FV, так и PV.
Например, 5-процентная ставка приносит будущий доход в размере $105 за 1 год.
Какой должна быть текущая (первоначальная) сумма, вложенная под 5%, чтобы она выросла до $105 через 1 год?
Ответ: $100 представляют собой текущую стоимость (PV) для будущей суммы (FV) в размере $105, которая должна быть получена через 1 год, при ставке вклада 5%.
Используя будущий денежный поток, который должен быть получен в течение N периодов, и процентную ставку за период r, мы можем преобразовать формулу (2) будущей стоимости денежного потока следующим образом:
FVN = PV * (1 + r)N
\( \mathbf { PV=FV_N \left[ 1 \over (1+r)^N \right] }\)
PV = FVN * [1 / (1 + r)N] (формула 8)
или
PV = FVN * (1 + r)-N
Из формулы 8 видно, что фактор текущей стоимости (англ. ‘present value factor’), (1 + r)-N является обратной величиной фактора будущей стоимости (1 + r)N.
Пример расчета текущей стоимости денежного потока.
Страховая компания выпустила гарантированный инвестиционный сертификат (GIC), который гарантирует выплату $100 000 в течение 6 лет с 8-процентной прибылью.
Какую сумму страховщик должен инвестировать сегодня, чтобы через 6 лет обеспечить выплату обещанной суммы по сертификату?
Решение:
Мы можем применить формулу 8, чтобы найти текущую (приведенную) стоимость, используя следующие данные:
FVN = $100,000
r = 8% = 0.08
N = 6
PV = FVN (1 + r)-N
= $100,000 * [1 / (1.0 8)6]
= $100,000 * (0.6301696) = $63,016.96
Можно сказать, что сегодня $63 016,96 при процентной ставке 8% эквивалентны $100 000, которые будут получены через 6 лет.
Дисконтирование сегодняшней суммы $100 000 делает будущую сумму в размере $100 000 эквивалентом $63 016,96, с учетом временной стоимости денег (TVM).
Как показывает временная линия на рисунке ниже, $100 000 дисконтированы в течение 6 полных периодов.
 Текущая стоимость (PV) $100 000 в момент времени t = 6.
Текущая стоимость (PV) $100 000 в момент времени t = 6.
Пример прогнозирования текущей стоимости денежного потока.
Предположим, что у вас есть ликвидный финансовый актив, который принесет вам $100 000 через 10 лет от текущей даты.
Ваша дочь планирует поступить в колледж через четыре года, и вы хотите знать, какова будет текущая (приведенная) стоимость актива к этому моменту.
С учетом 8% ставки дисконтирования, какова будет стоимость актива через 4 года от текущей даты?
Решение:
Стоимость актива ($100 000) — это текущая стоимость через 10 лет. При t = 4 эта сумма будет получена 6 лет спустя — см. рисунок ниже.
Связь между текущей и будущей стоимостью актива.
С помощью этой информации вы можете вычислить стоимость актива через 4 года от текущей даты, используя формулу 8:
FVN = $100,000
r = 8% = 0.08
N = 6
PV = FVN (1 + r)-N
= $100,000 * [1 / (1.08)6]
= $100,000 * (0.6301696)
= $63,016.96
Временная линия на рисунке выше показывает будущий платеж в размере $100 000, который должен быть получен при t = 10. На временной шкале также показана стоимость денежного потока при t = 4 и при t = 0.
По сравнению с суммой при t = 10, сумма при t = 4 представляет собой прогнозируемую текущую стоимость, а сумма при t = 0 является текущей приведенной стоимостью (на сегодняшний день).
Задачи, требующие вычисления текущей стоимости (PV) требуют определения фактора текущей стоимости
(1 + r)-N.
Текущая стоимость зависит от процентной ставки и количества периодов начисления процентов следующим образом:
- При заданной ставке дисконтирования, чем дальше в будущем будет получена сумма, тем меньше будет текущая стоимость (PV) этой суммы.
- Для одного и того же момента времени, с ростом ставки дисконтирования уменьшается текущая стоимость будущей суммы.
Расчет текущей (приведенной) стоимости с промежуточным начислением процентов.
Напомним, что проценты могут выплачиваться раз в полгода, ежеквартально, ежемесячно или даже ежедневно.
Для расчета процентных платежей, производимых более 1 раза в год, мы можем изменить формулу текущей стоимости (8).
Напомним, что rS — котируемая (заявленная) процентная ставка и она равна периодической процентной ставке, умноженной на количество периодов начисления в каждом году.
В целом, если в году есть более 1 промежуточного периода начисления, мы можем выразить формулу расчета текущей стоимости (PV) как:
PV = FVN * (1 + rS/m)-mN (формула 9)
где:
m = количество периодов начисления в году,
rS = заявленная годовая процентная ставка,
N = количество лет.
Формула 9 очень похожа на формулу 8.
Как мы уже отмечали, фактор текущей стоимости и фактор будущей стоимости являются обратными значениями по отношению друг к другу. И добавление в формулу частоты начисления процентов не влияет на эту взаимозависимость между двумя факторами.
Единственное различие заключается в использовании периодической процентной ставки и соответствующего количества периодов начисления.
Следующий пример иллюстрирует формулу 9.
Пример расчета текущей (приведенной) стоимость при ежемесячном начислении процентов.
Менеджер канадского пенсионного фонда знает, что фонд должен выполнить единовременный платеж в размере $5 млн. через 10 лет. Она планирует сегодня инвестировать некоторую сумму в гарантированный инвестиционный сертификат (GIC), чтобы эта инвестиция выросла до необходимой суммы в $5 млн.
Текущая процентная ставка по GIC составляет 6 процентов в год, с ежемесячным начислением процентов.
Сколько она должна сегодня инвестировать в GIC?
Решение:
Используя формулу 9, чтобы находим требуемую текущую стоимость:
FVN = $5,000,000
rS = 6% = 0.06
m = 12
rS / m = 0.06/12 = 0.005
N = 10
mN = 12*(10) = 120
PV = FVN * (1 + rS/m)-mN
= $5,000,000 * (1.005)-120
= $5,000,000 * (0.549633)
= $2,748,163.67
При применении формулы 9 мы используем периодическую ставку (в данном случае, месячную ставку) и соответствующее количество периодов с ежемесячным начислением процентов (в данном случае 10 лет ежемесячных начислений или 120 периодов).
fin-accounting.ru
Дисконтированная стоимость (PV) — что это. Формула и пример расчета в Excel
Оба понятия из заголовка этого раздела, дисконтированная (приведенная) стоимость, ПС (presentvalue, или PV), и чистая дисконтированная (приведенная) стоимость, ЧПС (netpresentvalue, или NPV), обозначают текущую стоимость ожидаемых в будущем денежных поступлений.
В качестве примера рассмотрим оценку инвестиции, обещающей доход 100 долл. в год в конце нынешнего и еще четырех следующих лет. Предполагаем, что эта серия из пяти платежей по 100 долл. каждый гарантирована и деньги непременно поступят. Если бы банк платил нам годовой процент в размере 10% при депозите на пять лет, то эти десять процентов как раз и составляли бы альтернативную стоимость инвестиции — эталонную норму прибыли, с которой мы сравнивали бы выгоду от нашего вложения.
Можно вычислить ценность инвестиции путем дисконтирования денежных поступлений от нее с использованием альтернативной стоимости в качестве ставки дисконтирования.
Формула расчета в Excel дисконтированной (приведенной) стоимости (PV) = ЧПС(C1;B5:B9)
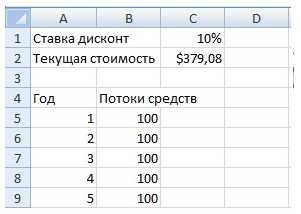
Приведенная стоимость (ПС) в объеме 379,08 долл. и есть текущая стоимость инвестиции.
★ Инвестиционная оценка в Excel. Расчет NPV, IRR, DPP, PI за 5 минут
Предположим, что данная инвестиция продавалась бы за 400 долл. Очевидно, она не стоила бы запрашиваемой цены, поскольку — при условии альтернативного дохода (учетной ставки) в размере 10% — реальная стоимость этого капиталовложения составляла бы только 379,08 долл. Здесь как раз уместно ввести понятие чистой приведенной стоимости (ЧПС). Обозначая символом r учетную ставку для данной инвестиции, получаем следующую формулу NPV:
Где СFt – денежное поступление от инвестиции в момент t; CF0 –поток средств (поступление) на текущий момент.
Формула расчета в Excel чистой дисконтированной (приведенной) стоимости (NPV) = ЧПС(C1;B6:B10)+B5
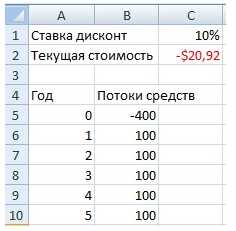
Терминология Excel, касающаяся дисконтируемых потоков денежных средств, несколько отличается от стандартной финансовой терминологии. В Excel сокращение МУР (ЧПС) обозначает приведенную стоимость (а не чистую приведенную стоимость) серии денежных поступлений.
Чтобы рассчитать в Excel чистую приведенную стоимость серии денежных поступлений в обычном понимании финансовой теории, необходимо сначала вычислить приведенную стоимость будущих денежных поступлений (с использованием такой функции Excel, как “ЧПС”), а затем вычесть из этого числа денежный поток на начальный момент времени. (Эта величина часто совпадает со стоимостью рассматриваемого актива.)
Автор: к.э.н. Жданов Иван Юрьевич
finzz.ru
Present Value PV — Финансовый словарь смарт-лаб.
PV — Present Value — Текущая стоимость актива.Приведенная к текущему моменту стоимость будущих денежных потоков объекта.
см. также: FV — Future Value
PV и FV связаны простым взаимоотношением:
FV = PV (1 + r) n
PV = FV (1 + r)-n (1)
Пример использования:
Нам известно, что хотим накопить $100 000 в течение 6 лет. Мы знаем, что ставка по депозиту составляет 8% годовых, а значит, можем рассчитать необходимый начальный объем вложений, чтобы получить требуемую выплату:
PV = $100 000/(1 + 1,08)6 = $63 016
Текущая стоимость будущих равномерных платежей (present value of a series of equal cash flow) вычисляется по формуле (2):
Пример задачи:
есть финансовый актив, который будет приносить вам 1000 долларов в год дохода в течение 20 лет начиная через год от текущего момента, при рыночной ставке =12%. Оценить текущую стоимость актива. В этом случае значения можно просто подставлять в формулу.
Если актив начинает приносить доход первый доход 1000 с первого дня его приобретения, то в формулу вместо 20 вставляем 19, и просто к полученному значению прибавляем 1000.
Вычисление present value, когда выплаты начинаются с определенного срока в будущем (Tx).
В этом случае, надо использовать формулу (2) для того чтобы подсчитать PV на момент Tx, а потом вычислить PV на текущий момент по формуле (1), где PV(Tx) станет обычным FV.
Текущая стоимость (present value) суммы регулярных бесконечных денежных потоков вычисляется очень просто:
PV=FV/A
Текущая стоимость неоднородных денежных потоков вычисляется как сумма отдельно взятых дисконтированных доходов:

Измерение FV и PV полезно для сравнения альтернативных способов инвестирования потому что оценка потоков должна быть проведена в одинаковых точках времени — в конце инвест горизонта (FV) или в начале (PV).
smart-lab.ru
CFA — Как рассчитывать будущую стоимость денежного потока (FV)? | программа CFA
Существует взаимосвязь между первоначальной инвестицией (PV), которая приносит доход по процентной ставке r за период, и будущей стоимостью (FV) этой инвестиции, которая будет получена через N лет или периодов.
Следующий пример иллюстрирует эту концепцию FV.
Предположим, вы вкладываете $100 (PV = 100) на депозитный банковский счет, который приносит доход 5% в год.
В конце 1 года вы получите $100 плюс проценты, рассчитываемые как 0,05 * 100 = $5, что в общей сложности составляет $105.
Чтобы формализовать этот пример расчета FV за 1 период, мы определяем следующие термины:
- PV = текущая или первоначальная стоимость инвестиций (англ. ‘present value’).
- FVN = будущая стоимость инвестиций через N периодов от текущей даты (англ. ‘future value’).
- r = процентная ставка за период.
Для N = 1 формула для расчета будущей стоимости PV будет такой:
FV1 = PV * (1 + r) (формула 1).
В этом примере мы вычисляем будущую стоимость через 1 год от текущей даты:
FV1 = $100 * (1.05) = $105.
Теперь предположим, что вы решили инвестировать первоначальные $100 на 2 года с учетом суммы процентов, начисляющихся на ваш счет ежегодно (т.е. при ежегодном начислении сложных процентов).
В конце 1 года (на начало 2 года) на вашем счете будет $105, которые вы оставите в банке еще на год. Таким образом, при начальном размере инвестиций в $105 (PV = 105), сумма на конец второго года составит $105 * (1,05) = $110,25.
Обратите внимание, что проценты в размере $5,25, полученные за 2 год, составляют 5% от суммы, оставшейся на банковском счете на начало 2 года.
Еще один способ понять этот пример — отметить, что сумма, вложенная в начале 2-го года, состоит из первоначальной суммы в $100 плюс проценты $5, заработанные в течение 1-го года. В течение 2-го года первоначальная сумма вклада снова приносит проценты, а также проценты от процентов, которые были заработаны за 1-й год.
В приведенной ниже таблице вы более наглядно можете увидеть, как растут первоначальные инвестиции:
|
Первоначальные инвестиции |
$100 |
|
Проценты за 1 год ($100 * 0.05) |
5 |
|
Проценты за 2 год от первоначальных инвестиций (100 * 0,05) |
5 |
|
Проценты за 2 год от процентов, полученных за 1 год (0,05 * 5) |
0,25 |
|
Итого |
$110,25 |
Процентный доход в размере $5, полученный за каждый период от первоначальных инвестиций в размере $100, известен как простой процент (англ. ‘simple interest’): процентная ставка, умноженная на основную сумму.
Основная сумма (англ. ‘principal’) — это сумма первоначально вложенных средств.
В течение двухлетнего периода вы получаете простые проценты в размере $10. Дополнительные $0,25, которые у вас образовались в конце 2 года, — это проценты, начисленные на сумму процентов в $5, которую вы заработали за 1 год и реинвестировали.
Проценты, полученные по процентам в этом примере, дают представление о явлении, которое известно как компаундинг или наращение или капитализация процентов или просто начисление сложного процента (англ. ‘compounding’).
Сложный процент, полученный от реинвестирования процентов, обеспечивает сильный эффект наращения инвестиций, потому что при заданной процентной ставке сумма процентов растет в каждом периоде.
Эффект наращения процентов усиливается с ростом величины процентной ставки. Например, $100, вложенные сегодня, стоили бы около $13 150 через 100 лет при начислении сложного процента по ставке 5%, но они также стоили бы более $20 млн. за тот же период при ставке 13%.
Чтобы проверить это, нам нужна общая формула, позволяющая рассчитать сложный процент для любого количества периодов. Следующая общая формула связывает текущую стоимость первоначальных инвестиций с их будущей стоимостью через N периодов:
FVN = PV * (1 + r)N, (формула 2)
где
- r — процентная ставка за период, а
- N — количество периодов наращения процентов.
В примере с банком расчет будет таким:
FV2 = $100 * (1 + 0,05) 2 = $110,25.
В примере с инвестициями по ставке 13%:
FV100 = $100 * (1.13) 100 = $20 316 287.42.
Наиболее важным моментом, о котором следует помнить при использовании формулы будущей стоимости денежного потока FV, является то, что процентная ставка r и количество периодов наращения N должны соответствовать общему временному периоду. То есть, обе эти переменные должны быть определены в одних и тех же единицах времени.
Например, если N указана в месяцах, тогда r должна быть 1-месячной процентной ставкой.
Временная линия помогает нам отслеживать соответствие единиц времени процентной ставки и периодов. На графике временной линии мы используем знак t, чтобы отметить момент начала / окончания периода. Он также обозначает номер (индекс) определенного периода.
Таким образом, текущая стоимость PV представляет собой сумму, которую можно инвестировать в текущую дату с номером t = 0. Мы можем ссылаться на момент окончания инвестиционного периода (срок возврата средств) как на t = N.
Временная линия на рисунке ниже показывает эту связь.
Связь между первоначальными инвестициями PV и их будущей стоимостью FV.
На графике ниже первоначальные инвестиции PV отражены в периоде t = 0. Используя формулу (2), мы перемещаем текущее значение PV вперед, к периоду t = N, с помощью коэффициента (1 + r)N.
Этот коэффициент называется фактором будущей стоимости (англ. ‘future value factor’).
Обозначим будущую стоимость на временной линии как FV и расположим ее в точке t = N. Предположим, что будущее значение должно быть получено ровно через 10 периодов от текущей даты (N = 10).
Текущая стоимость PV и будущая стоимость FV разделены во времени через коэффициент (1 + r)10.
Тот факт, что текущая стоимость и будущая стоимость разделены во времени, имеет важные последствия:
- Мы можем добавлять суммы денег только в том случае, если они индексируются в тот же момент времени.
- При заданной процентной ставке r, будущая стоимость FV увеличивается с ростом количества периодов N.
- Для данного количества периодов N, будущая стоимость FV увеличивается с ростом процентной ставки r.
Чтобы лучше понять эти концепции, рассмотрим три примера, иллюстрирующих применение формулы будущей стоимости.
Пример (1) расчета будущей стоимости FV с реинвестированием процентов по той же процентной ставке.
Допустим, вы — счастливый победитель лотереи с призом в размере $5 млн. после уплаты налогов. Вы инвестируете свой выигрыш в 5-летний депозитный сертификат (CD) в местном банке. CD обещает ежегодную выплату по годовой процентной ставке 7%.
Это банк также позволяет реинвестировать проценты по той же процентной ставке в течение срока действия депозитного сертификата.
Какую сумму вы заработаете через 5 лет, если будете реинвестировать начисленные проценты по ставке 7% в течение пяти лет?
Решение:
Вычислим будущую стоимость инвестиций FV, используя в формуле следующие значения в:
PV = $5,000,000
r = 7% = 0.07
N = 5
FVN = PV * (1 + r)N
= $5,000,000 * (1.07)5
= $5,000,000 * (1.402552)
= $7,012,758.65
По истечении 5 лет у вас будет $7,012,758.65.
Обратите внимание, что фактор будущей стоимости округлен до шести десятичных знаков после нуля, но расчет может фактически отражать большую точность.
Например, фактор будущей стоимости в примере 1.402552 был округлен от 1.40255173, но расчет фактически выполняется (калькулятором или электронной таблицей) с фактором более 8 десятичных знаков после нуля.
Пример (2) расчета будущей стоимости FV без реинвестирования процентов.
Финансовая организация предлагает вам следующие условия: за инвестиции в размере ¥2 500 000 компания обещает выплатить вам единовременную сумму через 6 лет по годовой процентной ставке 8%.
Какова будет будущая стоимость инвестиций?
Решение:
Используйте следующие данные в формуле 2, чтобы найти будущую стоимость FV:
PV = ¥2,500,000
r = 8% = 0.08
N = 6
FVN = PV * (1 + r)N
= ¥2,500,000 * (1.08)6
= ¥2,500,000 * (1.586874)
= ¥3,967,186
Через 6 лет вы получите ¥3,967,186.
Наш третий пример — более сложная задача расчета FV, которая иллюстрирует важность отслеживания фактических календарных сроков.
Пример (3) расчета будущей стоимости с отсроченной единовременной инвестицией.
Менеджер пенсионного фонда ожидает, что его корпоративный клиент внесет $10 млн. через 5 лет от текущей даты. Норма прибыли активов фонда оценивается в 9% годовых.
Менеджер пенсионного фонда хочет рассчитать будущую стоимость этого взноса через 15 лет от текущей даты, то есть на дату, когда средства будут распределены пенсионерам.
Какой будет будущая стоимость?
Решение:
При индексе периода t = 5 мы можем рассчитать будущую стоимость вклада, используя следующие данные в формуле 2:
PV = $10,000,000
r = 9% = 0.09
N = 10
FVN = PV * (1 + r)N
= $10,000,000 * (1.09)10
= $10,000,000 * (2.367364)
= $23,673,636.75
Эта задача очень похожа на предыдущие две, но есть одно важное отличие: временная линия инвестиций.
С текущей даты (t = 0) будущая стоимость через 15 лет составит $23 673 636,75.
Хотя будущая стоимость FV соответствует 10-летнему сроку начисления процентов, первоначальная стоимость в $10 млн. будет получена только через 5 лет от текущей даты.
Будущая стоимость (FV) при первоначальной инвестиции t ≠ 0.
Как показано на графике выше, первоначальные инвестиции в размере $10 млн. должны быть осуществлены через 5 лет, поэтому эта сумма индексируется как t = 5 и отображается на временной линии в соответствующей точке.
Будущая стоимость инвестиций FV через 10 лет индексируется как t = 15, то есть 10 + 5.
Временные линии, подобные приведенной выше, могут быть чрезвычайно полезными при решении более сложных задач, особенно тех, которые связаны с несколькими потоками денежных средств.
Предположим, что менеджер пенсионного фонда также должен получить сегодня от корпоративного клиента $6,499,313,86.
Сколько будет стоить эта сумма через 5 лет?
Сколько она будет стоить через 15 лет?
PV = $6,499,313.86
r = 9% = 0.09
N = 5
FVN = PV * (1 + r)N
= $6,499,313.86 * (1.09)5
= $6,499,313.86 * (1.538624)
= $10,000,000 через 5 лет.
А также:
PV = $6,499,313.86
r = 9% = 0.09
N = 15
FVN = PV * (1 + r)N
= $6,499,313.86 * (1.09)15
= $6,499,313.86 * (3.642482)
= $23,673,636.74 через 15 лет.
Частота начисления процентов.
Рассмотрим инвестиции, для которых проценты выплачиваются более одного раза в год, т.е. инвестиции с разной частотой начисления процентов (англ. ‘compounding frequency’).
Например, многие банки предлагают ежемесячную процентную ставку, которая начисляется 12 раз в год. По такому вкладу банки начисляют проценты на проценты каждый месяц.
Вместо того, чтобы указывать периодическую ежемесячную процентную ставку, финансовые учреждения часто ссылаются на годовую процентную ставку, которую мы называем заявленной годовой процентной ставкой (англ. ‘stated annual interest rate’) или котируемой процентной ставкой (англ. ‘quoted interest rate’).
Заявленная годовая процентная ставка обозначается в формулах как rS. Заявленная годовая процентная ставка равна месячной процентной ставке, умноженной на 12.
Например, ваш банк может заявить, что за определенный депозит он платит 8% ежемесячно. В этом случае месячная процентная ставка составляет 0,08 / 12 = 0,0067 или 0,67%.
Эта ставка является сугубо ориентировочным значением, поскольку (1 + 0,0067) 12 = 1,083, а не 1.08. Значение (1 + rS) не является фактором будущей стоимости для расчета процентов за период меньше 1 года.
Формула будущей стоимости может быть выражена в виде более чем одного периода составления отчетности в год.
FVN = PV * (1 + rS / m) mN (формула 3),
где
- rS — заявленная годовая процентная ставка,
- m — количество составляющих периодов года,
- а N обозначает количество лет.
Обратите внимание на совместимость между заявленной процентной ставкой, периодической ставкой rS / m и количеством периодов начисления mN.
Периодическая ставка (англ. ‘periodic rate’) rs/m представляет собой заявленную годовую процентную ставку, деленную на количество периодов начисления в году.
Общее количество периодов начисления mN, представляет собой количество периодов начисления за 1 год, умноженное на количество лет.
Периодическая ставка rS / m и количество периодов начисления mN должны быть совместимыми.
Пример (4) расчета будущей стоимости FV с ежеквартальным начислением процентов.
Продолжая пример с депозитным сертификатом, предположим, что ваш банк предлагает вам депозит с 2-летним сроком. Заявленная годовая процентная ставка в размере 8% начисляется ежеквартально, а также есть возможность реинвестирования процентов по той же процентной ставке. Вы решили вложить $10 000.
Сколько будет стоить депозит к моменту его закрытия?
Решение:
Вычислим будущую стоимость с помощью формулы (3) следующим образом:
PV = $10,000
rS = 8% = 0.08
m = 4
rS / m = 0.08/4 = 0.02
N = 2
mN = 4 * (2) = 8 периодов начисления
FVN = PV * (1 + rS / m)mN
=$10,000 * (1.02)8
= $10,000 * (1.171659)
= $11,716.59
К моменту закрытия депозит будет стоить $11,716.59.
Формула 3 не отличается от формулы 2. Просто имейте в виду, что в ней используется периодическая процентная ставка, а экспонента — это общее количество периодов начисления.
Пример (5) расчета будущей стоимости FV с ежемесячным начислением процентов.
Банк предлагает вклад под 6% с ежемесячной выплатой начислений. Вы решили инвестировать $1 млн. на 1 год.
Какова будущая стоимость ваших инвестиций, если процентные платежи реинвестируются под 6%?
Решение:
Используя формулу 3, найдем будущую стоимость инвестиции следующим образом:
PV = $1,000,000
rS = 6% = 0.06
m = 12
rS / m = 0.06/12 = 0.0050
N = 1
mN = 12 * (1) = 12 периодов начисления
FVN = PV * (1 + rS / m)mN
= $1,000,000 * (1.005)12
= $1,000,000 * (1.061678)
= $1,061,677.81
Если бы вам выплачивали 6% с годовым начислением, будущая стоимость составляла бы всего 1 000 000 * (1.06) = $1 060 000 вместо $1 061 677,81 при ежемесячном начислении.
Непрерывное начисление сложных процентов.
Приведенное выше обсуждение периодов начисления сложных процентов иллюстрирует дискретное начисление, связанное с расчетом процентов за определенный период времени.
Если количество периодов начисления в год становится бесконечным, то такое начисление процентов считается непрерывным.
Если мы хотим использовать формулу будущей стоимости FV с непрерывным начислением, нам нужно найти предельное значение фактора будущей стоимости для m → ∞ (т.е. бесконечно много периодов начисления в год) в формуле 3.
Формула для будущей стоимости суммы через N лет с непрерывным начислением:
\(\mathbf{FV_N= PVe^{r_SN} }\) (формула 4)
Выражение \(\mathbf{e^{r_SN} }\) является трансцендентальным числом e ≈ 2,7182818, возведенным в степень rS * N. Большинство финансовых калькуляторов имеют функцию ex.
Пример (6) расчета будущей стоимости FV с непрерывным начислением процентов.
Предположим, что инвестиции в размере $10 000 будут приносить 8% годовых с непрерывным начислением в течение 2 лет.
Мы можем вычислить будущее значение с помощью формулы 4 следующим образом:
PV = $10,000
rS = 8% = 0.08
N = 2
FVN = \(\mathbf{PVe^{r_SN} }\)
= $10,000 * e0.08(2)
= $10,000 * (1.173511)
= $11,735.11
При такой же процентной ставке, но с использованием непрерывного начисления инвестиции в размере $10 000 вырастут до $11 735,11 за два года по сравнению с $11 716,59 при ежеквартальном начислении, как показано в примере 4.
В таблице ниже показано, как заявленная годовая процентная ставка в размере 8% генерирует разные суммы будущей стоимости при годовом, полугодовом, ежеквартальном, ежемесячном, ежедневном и непрерывном начислении для первоначальной инвестиции в размере $1 (с округлением результата до шести знаков после запятой).
Как видно из таблицы, все шесть вариантов начисления имеют одинаковую процентную ставку в 8%, но дают разные результаты из-за различий в частоте начисления процентов (англ. ‘compounding frequency’).
Более частое начисление приводит к увеличению итоговой будущей стоимости FV. Итоговая сумма при непрерывного начисления — это максимальный результат, который можно получить при заявленной годовой ставке 8%.
|
Частота |
rS / m |
mN |
Будущая стоимость $1 |
|
|---|---|---|---|---|
|
Годовая |
8%/l = 8% |
1 * 1 = 1 |
$1.00 * (1.08) |
=$1.08 |
|
Полугодовая |
8%/2 = 4% |
2 * 1 = 2 |
$1.00 * (1.04)2 |
=$1.081600 |
|
Квартальная |
8%/4 = 2% |
4 * 1 = 4 |
$1.00 * (1.02)4 |
=$1.082432 |
|
Ежемесячная |
8%/12 = 0.6667% |
12 * 1 = 12 |
$1.00 * (1.006667)12 |
=$1.083000 |
|
Ежедневная |
8%/365 = 0.0219% |
365 * 1 = 365 |
$1.00 * (1.000219)365 |
=$1.083278 |
|
Непрерывная |
$1.00е0.08(1) |
=$1.083287 |
||
Из таблицы также видно, что доход от инвестиций в размере $1, по ставке 8,16% при годовом начислении даст такой же доход как ставка 8% при полугодовом начислении.
Этот результат приводит нас к различию между заявленной годовой процентной ставкой и эффективной годовой процентной ставкой (EAR, от англ. ‘effective annual rate’).
Для заявленной годовой процентной ставки в 8% с полугодовым начислением EAR составляет 8,16%.
Среди терминов, используемых для обозначения эффективной годовой доходности по процентным банковским депозитам, следует упомянуть:
- Годовую процентную доходность (APY от англ. ‘annual percentage yield’) используемую в США.
- Эквивалентную APY эффективную годовую процентную ставку (EAR, от англ. ‘effective annual rate’), используемую в Великобритании.
- В отличие от APY и EAR, годовая процентная ставка (APR, от англ. ‘annual percentage rate’) измеряет стоимость заимствований и выражается годовой процентной ставкой.
В США APR рассчитывается как периодическая ставка, умноженная на количество периодов оплаты в год, в результате чего некоторые авторы используют APR в качестве общего синонима для заявленной годовой процентной ставки.
Тем не менее, APR — это термин с юридическим подтекстом. Расчет APR соответствует нормативным стандартам, которые меняются на международном уровне.
Поэтому «заявленная годовая процентная ставка» является предпочтительным общим термином для годовой процентной ставки в годовом исчислении, которая не учитывает промежуточные начисления в течение года.
Заявленные и эффективные процентные ставки.
Заявленная годовая процентная ставка не позволяет рассчитать будущую стоимость напрямую, поэтому для этого нам нужна формула EAR.
Для годовой процентной ставки 8, начисляемой раз в полгода, мы получаем периодическую ставку в 4% (8% / 2).
В течение года инвестиции в размере $1 вырастут до $1 * (1.04)2 = $1.0816, как показано в таблице выше. Проценты, полученные от инвестиций в размере $1, составляют $0,0816 и представляют собой эффективную годовую процентную ставку в размере 8,16%.
Эффективная годовая ставка рассчитывается следующим образом:
EAR = (1 + Периодическая процентная ставка) m — 1 (формула 5)
Периодическая процентная ставка (англ. ‘periodic interest rate’) представляет собой заявленную годовую процентную ставку, деленную на m, где m — количество периодов начисления в 1 году.
Используя предыдущий пример, мы можем рассчитать EAR следующим образом:
(1.04)2 — 1 = 8,16%.
Примеры использования EAR в финансовых вычислениях: см. CFA — Как вычислять эффективную годовую процентную ставку (EAR)?
Концепция EAR распространяется на непрерывное начисление процентов.
Предположим, что проценты по ставке 8% начисляются непрерывно. Мы можем вычислить EAR так же, как и выше, найдя соответствующий фактор будущей стоимости.
В этом случае инвестиции в $1 вырастут до $1e0.08(10) = $1.0833.
Проценты, полученные за 1 год, представляет собой эффективную годовую ставку в 8,33%, что больше, чем EAR в 8,16% с полугодовым начислением, поскольку проценты начисляются чаще.
При непрерывном начислении мы можем рассчитать эффективную годовую ставку следующим образом:
EAR = \(\mathbf{e^{r_S} }\) — 1 (формула 6)
Мы можем изменить формулу для EAR с дискретным и непрерывным начислением, чтобы найти периодическую ставку, соответствующую конкретной эффективной годовой ставке.
Предположим, мы хотим найти соответствующую периодическую ставку для EAR 8,16% с полугодовым начислением.
Мы можем использовать формулу 5 для расчета периодической ставки:
0,0816 = (1 + периодическая ставка)2 — 1
1.0816 = (1 + периодическая скорость)2
Периодическая ставка =
(1.0816)1/2 — 1 =
(1,04) — 1 = 4%
Чтобы рассчитать непрерывно начисляемую ставку (заявленную годовую процентная ставку с непрерывным начислением), соответствующую эффективной годовой ставке 8,33%, мы находим процентную ставку, которая удовлетворяет уравнению формулы 6:
0,0833 = \(\mathbf{e^{r_S} }\) — 1
1.0833 = \(\mathbf{e^{r_S} }\)
Для решения этого уравнения находим натуральный логарифм обеих сторон. (Напомним, что натуральный логарифм \(\mathbf{e^{r_S} }\) равен \(\mathbf{ln \ e^{r_S} = r_S }\) ).
Следовательно, ln 1.0833 = rS, а rS = 8%.
Мы видим, что заявленная годовая ставка 8% с непрерывным начислением эквивалентна EAR в 8,33%.
Выше мы рассмотрели порядок расчета будущей стоимости для единичного денежного потока.
Для расчета серии денежных потоков см.: CFA — Как рассчитывать будущую стоимость последовательности денежных потоков (аннуитет)?
fin-accounting.ru
Об авторе