Как стать общим другом в вк: Как добавить в общие друзья ВКонтакте

Содержание

ML на эго-графах / Хабр

Дружбы — одна из важнейших механик любой социальной сети. Подавляющее большинство взаимодействий происходит между пользователями, которые дружат: мы видим и комментируем записи друг друга в лентах, заходим в список друзей, чтобы найти знакомых и написать сообщение. Именно поэтому рост социального графа так важен.

Меня зовут Женя Замятин, я работаю в команде Core ML ВКонтакте. Хочу рассказать, как устроены рекомендации, которые делают ближе пользователей самой крупной социальной сети рунета.

Обзор

Современные рекомендательные системы зачастую состоят из двух уровней, и наша не исключение. Задача первого уровня — искать наиболее релевантных кандидатов среди всего множества пользователей (у нас их сотни миллионов). Такая постановка задачи подразумевает высокую скорость работы. Обычно здесь используют простые в применении модели — вроде матричных факторизаций или эвристики на базе числа общих друзей. Полученные на первом уровне кандидаты отправляются на второй. Здесь на модель уже не накладываются такие жёсткие ограничения по скорости, её главная задача — обеспечить максимальную точность предсказаний и сформировать список, который увидит пользователь. В этой статье мы рассмотрим только первый этап — уровень отбора кандидатов.

Прежде всего сформулируем задачу, которую будем решать: для каждого пользователя необходимо найти k кандидатов, которых он с наибольшей вероятностью добавит в друзья. Метрика, на которую будем ориентироваться, — recall@k. Она идеально описывает задачу: на первом уровне нам не интересен порядок кандидатов, но важна их релевантность.

Сначала рассмотрим базовые решения, придуманные десятки лет назад, но до сих пор актуальные. Первым приходит на ум одно из самых логичных — эвристика на основе числа общих друзей. Для каждого пользователя отбираются кандидаты с наибольшим таким значением. Этот подход просто реализуется и неплох по качеству.

Ещё один важный метод рекомендаций — Adamic/Adar. В его основе лежит всё тот же анализ общих друзей, но с модификацией: авторы предлагают учитывать число друзей у «общего» друга.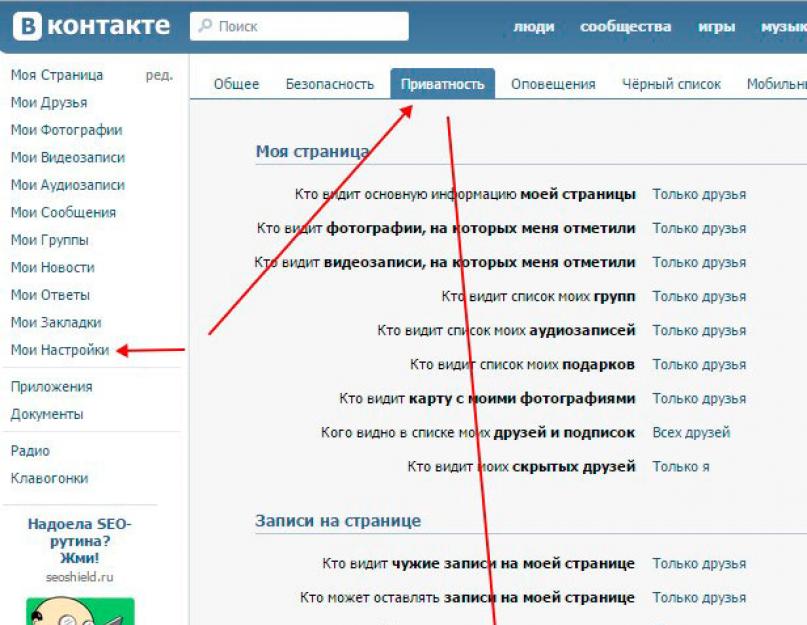 Чем больше это значение, тем меньше информации о релевантности он несёт.

Кроме методов на основе анализа общих друзей, довольно распространены рекомендации на базе эмбеддингов. В Лаборатории искусственного интеллекта ВКонтакте в МФТИ мы провели исследование: сравнили эффективность разных подходов к задаче предсказания дружб в VK. Результаты совпали с нашим опытом — решения на базе графовых эмбеддингов у нас работают плохо. Учитывая это, мы стали развивать систему отбора кандидатов по пути анализа общих друзей.

EGOML

Общая схема нашего метода продолжает идеи числа общих друзей и Adamic/Adar. Финальная мера релевантности E(u, v), с помощью которой мы будем отбирать кандидатов, всё так же раскладывается в сумму по общим друзьям u и v. Ключевое отличие — в форме слагаемого под суммой: в нашем случае это мера ez_c(u, v).

Сначала попробуем понять «физический» смысл меры ez_c(u, v). Представим, что мы взяли пользователя c и спросили у него: «Насколько вероятно, что два твоих друга, u и v, подружатся?» Чем больше информации для оценки он учтёт, тем точнее будет его предсказание.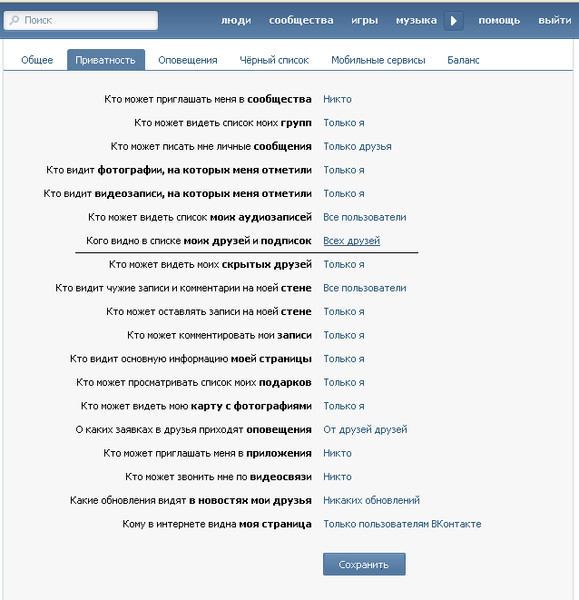 Например, если c сможет вспомнить только число своих друзей, его рассуждения могут выглядеть следующим образом: «Чем больше у меня друзей, тем менее вероятно, что случайные двое из них знакомы». Тогда оценка вероятность дружбы u и v (с точки зрения c) может выглядеть как 1/log(n), где n — число друзей. Именно так устроен Adamic/Adar. Но что если c возьмёт больше контекста?

Прежде чем отвечать на этот вопрос, разберёмся, почему ez_c(u, v) важно определять через пользователя c. Дело в том, что в таком виде очень удобно решать задачу распределённо. Представим, что теперь мы разослали всем пользователям платформы анкету с просьбой оценить вероятность дружбы в каждой паре их друзей. Получив все ответы, мы можем подставить значения в формулу E(u, v). Именно так выглядит вычисление E(u, v) с помощью MapReduce:

Подготовка. Для каждого c выделяется тот контекст, который он будет учитывать для вынесения оценок. Например, в Adamic/Adar это будет просто список друзей.
Map. «Спрашиваем» у каждого c, что он думает про возможность дружбы в каждой паре его друзей. По сути, вычисляем ez_c(u, v) и сохраняем в виде (u, v) → ez_c(u, v) для всех u, v in N(c). В случае Adamic/Adar: (u, v) → 1/log|N(c)|.
Reduce. Для каждой пары (u, v) суммируем все соответствующие ей значения. Их будет ровно столько, сколько общих друзей у u и v.

Таким образом мы получаем все ненулевые значения E(u, v). Заметим: необходимое условие того, что E(u, v) > 0, — существование хотя бы одного общего друга у u и v.

Эго-граф Хоппера

Контекстом пользователя c в случае меры ez_c будет тот же список друзей, но дополненный информацией о связях внутри этого списка. Такую структуру в науке называют эго-графом. Если более формально, эго-граф вершины x — это такой подграф исходного графа, вершинами которого являются все соседи x и сама x, а рёбрами — все рёбра исходного графа между этими вершинами. Коллеги из Одноклассников написали подробную статью об эго-графах и затронули в ней вопрос их эффективного построения.

Ключевая идея меры ez_c в том, что её можно сделать обучаемой. Для каждого пользователя c, его эго-графа и всех пар пользователей u, v внутри него мы можем посчитать много разных признаков, например:

число общих друзей u и v внутри эго-графа c;
число общих друзей u и c;
интенсивность взаимодействий между v и c;
время, прошедшее с последней дружбы между u и кем-либо из эго-графа c;
плотность эго-графа c;
и другие.

Таким образом мы получим датасет с признаками. Но для обучения нужны ещё и метки. Пусть датасет был построен по состоянию графа на момент времени T. Тогда в качестве положительных примеров возьмём те пары пользователей, которые не были друзьями на момент T, но подружились к T + △T. А как отрицательные — все остальные, не подружившиеся, пары пользователей. Заметим: поскольку мы решаем задачу предсказания новых дружб, те пары пользователей, которые уже дружат на момент T, учитывать не нужно ни на обучении, ни на применении.

В конечном счёте мы получаем датасет следующего вида:

для каждой пары пользователей u и v, а также их общего друга c, посчитаны признаки по эго-графу c;
пара пользователей u и v встречается в датасете ровно столько раз, сколько у них общих друзей;
все пары пользователей в датасете не являются друзьями на момент времени T;
для каждой пары u и v проставлена метка — подружились ли они в течение определённого промежутка времени начиная с T.

По такому датасету мы и будем обучать нашу меру ez_c. В качестве модели выбрали градиентный бустинг с pairwise функцией потерь, где идентификатором группы выступает пользователь u.
По сути, мера ez_c(u, v) определяется как предсказание описанной выше модели. Но есть один нюанс: при pairwise-обучении распределение предсказаний модели похоже на нормальное. Поэтому, если в качестве определения меры ez_c(u, v) взять «сырое» предсказание, может возникнуть ситуация, когда мы будем штрафовать финальную меру E(u, v) за общих друзей, так как значения предсказаний бывают отрицательными. Это выглядит не совсем логично — хочется, чтобы с ростом числа общих друзей мера E(u, v) не убывала. Так что поверх предсказания модели мы решили взять экспоненту:

Такой подход хорошо себя показывает на небольших графах. Но чтобы применить его на реальных данных, необходимо выполнить ещё одно действие. Суть проблемы такая: мы не можем вычислять признаки и применять модель для каждой пары пользователей всех эго-графов — это слишком долго. 2) до O(n). Но как получить такую модель, каждое дерево которой зависит только от одного пользователя? Для этого сделаем следующее:

Исключим из датасета все признаки, которые одновременно зависят и от u и от v. Например, от признака «число общих друзей u и v внутри эго-графа c» придётся отказаться.
Обучим модель A, используя только признаки на базе u, c и эго-графа c.
Для обучения модели B оставим только признаки на базе v, c и эго-графа c. Также в качестве базовых предсказаний передадим предсказания модели A.

Если объединим модели A и B, получим то что нужно: первая часть использует признаки u, вторая — признаки v. Совокупность моделей осмысленна, поскольку B была обучена «корректировать» предсказания A.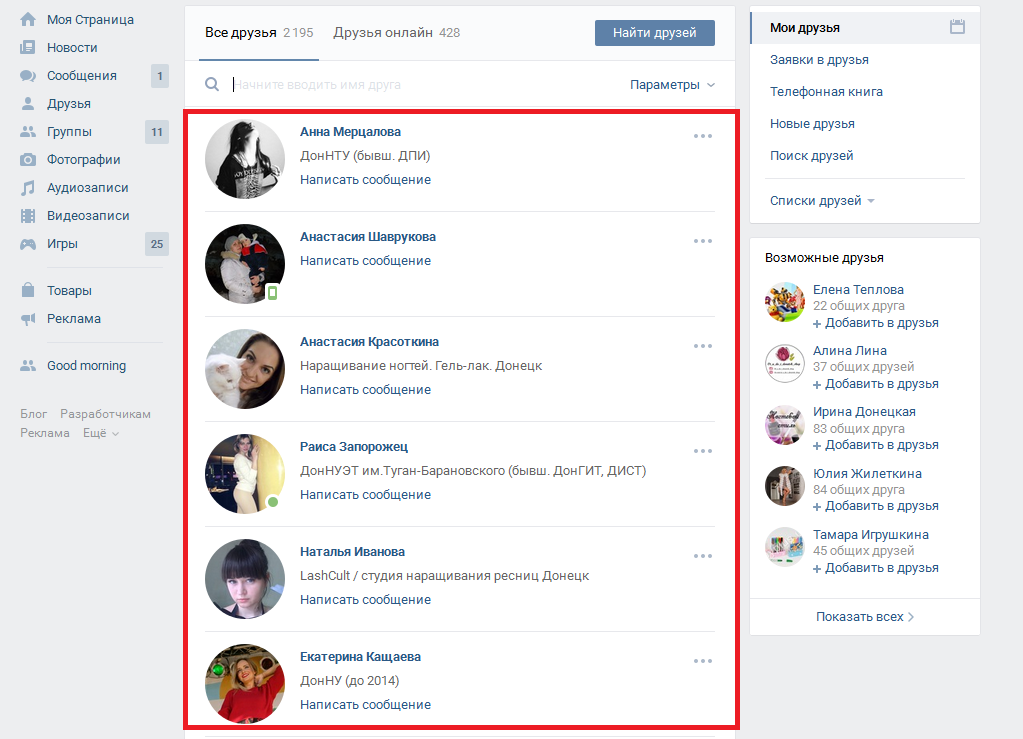 Эта оптимизация позволяет ускорить вычисления в сотни раз и делает подход применимым на практике. Финальный вид ez_c(u, v) и E(u, v) выглядит так:

Вычисление меры E в онлайне

Заметим, что E(u, v) можно представить в виде:

Эта формула — скалярное произведение разреженных векторов, индексами которых являются пользователи, а значениями — экспоненты предсказаний модели. Ненулевые значения здесь проставлены только у друзей u — по сути это просто списки друзей с дополнительными значениями.

При построении рекомендаций мы уже вычислили предсказания моделей для всех существующих дружб. Поэтому для каждого пользователя мы можем собрать векторы и сложить их в доступное онлайн key-value хранилище. После этого сможем получать значение E(u, v) для любой пары пользователей в онлайне простой операцией перемножения векторов. Это даёт возможность использовать E(u, v) как лёгкую функцию релевантности в нагруженных местах либо как дополнительный признак финальной модели ранжирования.

Итог

В результате система EGOML позволяет:

Распределённо отбирать кандидатов для каждого пользователя в офлайне. Асимптотическая сложность оптимизированного алгоритма составляет O(|E|) вычислений признаков и применений модели, где |E| — число связей в графе. На кластере из 250 воркеров время работы алгоритма составляет около двух часов.
Быстро вычислять меру релевантности E(u, v) для любой пары пользователей в онлайне. Асимптотическая сложность операции O(|N(u)| + |N(v)|).
Улучшать качество рекомендаций, расширяя количество учтённых графов (по дружбам, скрытиям рекомендаций, отправленным сообщениям и другим графам) и добавляя всевозможные метки на рёбра и вершины. Например, интенсивность взаимодействий на ребре, дату образования ребра, город, место работы или учёбы пользователя.

В конечном счёте мы перешли со способа отбора кандидатов с использованием Adamic/Adar к системе EGOML и внедрили в модель второй уровень признаков на основе меры E(u, v). И это позволило увеличить количество подтверждённых дружб со всей платформы на несколько десятков процентов.

Благодарность

Хочу сказать спасибо руководителю команды Core ML Андрею Якушеву за помощь в разработке метода и подготовке статьи, а также всей команде Core ML — за поддержку на разных этапах этой работы.

Как ВКонтакте определяются возможные друзья?

Определение возможных друзей ВК появилось уже сравнительно давно. Однако, это обновление до сих пор вызывает у пользователей соцсети много вопросов. И не странно, ведь не каждый знает, как вообще ВКонтакте определяются и предлагаются возможные друзья. Не все даже понимают смысл этого дополнения, и, тем более, не каждый им пользуется. И не зря у пользователей возникает множество вопросов, ведь нет четкого и понятного описания сервиса.

Оглавление

1 Где находятся возможные друзья
2 Основная цель сервиса
3 Можно ли увеличить список
4 Как появляются возможные друзья
- 4. 1 Возможные друзья на фейковых аккаунтах
5 Как убрать человека из «Возможных друзей»

Где находятся возможные друзья

Начать следует с простого. Определить расположение данного блока не так уж и сложно. Логично, что он находится в разделе «Друзья». Именно туда необходимо перейти со своей страницы, чтобы увидеть список возможных друзей.

С глобальным обновлением интерфейса поменялось и расположение данного блока. Раньше он отображался слева под меню страницы. Также его можно было найти с помощью сервиса поиска друзей.

После обновления изменились не только стандартные функции ВК, но и блок возможных друзей. Видимо, разработчики посчитали старое расположение не совсем удобным, поэтому переместили его. Теперь он находится справа, занимая отдельное пространство на вкладке «Друзья». Сделав переход по активной кнопке, можно будет ознакомиться с полным предоставленным списком. Также возможных друзей можно найти, как и прежде, перейдя по активной ссылке «Найти друзей».

Этот раздел может порекомендовать Вам тех, с кем Вы могли бы подружиться. Вы сразу же сможете нажать на иконку «Добавить в друзья». К запросу можно будет добавить сообщение, в котором указать, почему Вы решили пообщаться с этим пользователем.

При этом, человек получит уведомление с указанием количества Ваших общих друзей. Такой простой способ используют многие пользователи, желающие расширить свой френдлист.

Основная цель сервиса

Первоочередной идеей создания такой возможности стала потребность людей в поиске новых знакомств. Ведь это и было основной целью создания подобных социальных сетей. Зависит, от того, как посмотреть на саму идею соцсети.

Стоит упомянуть, что сервис рассчитан на людей, которые недавно зарегистрировались ВКонтакте. Блок «Возможные друзья» не будет появляться у пользователей с френдлистом более 100 человек. Тут же учитывается и количество подписок на разные сообщества. Таким образом, ВК позволяет новичкам не потеряться на сайте и сразу же приступить к общению и новым знакомствам.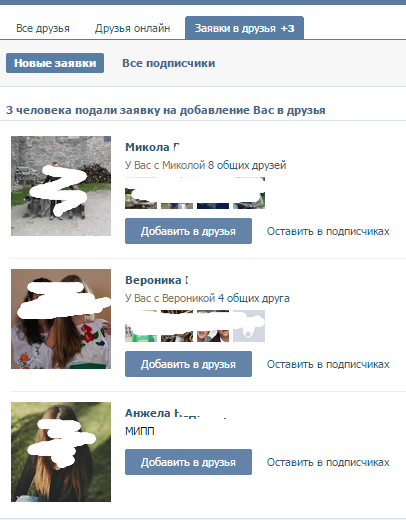

Также блок часто используют в целях коммерции. Многие увеличивают аудиторию своих групп и сообществ именно таким образом. Это разрешенная схема, ведь ВК сам предлагает пользователям добавить людей из списка рекомендованных. А предложить им вступить в группу никто не запрещает.

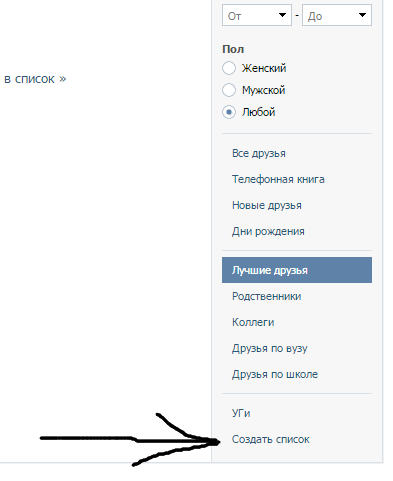
Можно ли увеличить список

Количество предлагаемых друзей ВКонтакте можно увеличить несколькими способами. При добавлении людей из уже существующего списка, Вы заметите, что он расширяется новыми общими друзьями. Это самый простой метод, которым пользуется большинство людей. Некоторые используют и накрутку.

В случае массового добавления в друзья ВКонтакте на страницы таких «накрутчиков», их рекомендации тоже будут пополняться. Для коммерческих проектов сервис просто незаменим.

Как появляются возможные друзья

В первую очередь, в списке оказываются люди, с которыми у Вас уже есть общие товарищи. Чем больше общих друзей тем выше предполагаемый друг, но сейчас влияет не только это.

Благодаря кнопке «Показать всех», можно будет увидеть более полный список Ваших возможных знакомых. Там будут появляться те же люди, только будет немного изменен порядок их расположения.

Далее для поиска рекомендаций используются такие параметры, как школы и ВУЗы (с учетом года окончания), родной город и даже участие в одном и том же сообществе или группе. Таким образом, предоставляется список не только реальных знакомых, но и тех, с кем могут совпадать интересы и предпочтения.

С помощью сервиса, многие нашли новых друзей и знакомых. А некоторым он не понравился. Ведь в их списке были абсолютно незнакомые люди. Это происходит потому, что многие добавляют в друзья тех, кого не знают. Таким образом, пользователи из их френдлиста попадут в «возможных друзей».

Возможные друзья на фейковых аккаунтах

Многие пользователи, создающие дополнительные страницы или фейки, обращают внимание на то, что ВК предлагает им подружиться с людьми из реальной жизни. Суть в том, что эти знакомые никак не пересекались с новой страницей, информация о них нигде не была указана. Пользователи даже начали переживать о безопасности своих данных. На это администрация соцсети ответила, что никакие данные и сведения не подлежат сбору и разглашению.

Некоторые сделали собственные выводы по этому поводу. Предполагается, что для определения возможных друзей ВК использует сохраненные куки. Также на компьютере или другом устройстве могут быть установлены разрешения, с помощью которых отслеживается статистика по посещению различных ресурсов. Таким образом, можно будет определить связь между реальной страницей и фейком, созданным на этом же устройстве.

Как убрать человека из «Возможных друзей»

Если в список попал человек, с которым Вам не хочется дружить, его легко можно будет убрать оттуда. Для этого необходимо курсором навести на крестик в углу аватарки пользователя. Там же высветится активное меню «Больше не показывать».

Это действие можно будет отменить. Удобность такой фильтрации в том, что люди, которые Вам не интересны, больше не будут появляться в списке рекомендованных, а их место займут те, с кем вы сможете познакомиться и общаться.

Такие дополнительные сервисы в соцсетях определенно указывают на то, что сайты рассчитаны, в первую очередь, на общение. Сегодня люди знакомятся, работают, влюбляются, да и живут в интернете. Поэтому такой незамысловатый поиск новых знакомых просто необходим для общества XXI века.

ВКонтакте друзья взаимные · GitHub

	#!/usr/bin/env python3
	#-- кодировка: UTF-8 —-

	импорт ОС, vk_api, sys
	из спящего режима импорта времени

	def captchaHandler(captcha):
	key = input(«Введите капчу {0}: «. format(captcha.get_url())).strip()
	вернуть captcha.try_again(ключ)
	определение getUserId (ссылка):
	идентификатор = ссылка
	если в ссылке «vk.com/»:
	идентификатор = ссылка.split(‘/’)[-1]
	, если не id.replace(‘id’, »).isdigit():
	id = vk.utils.resolveScreenName(screen_name=id)[‘object_id’]
	иначе:
	id = id.replace(‘id’, »)
	вернуть целое (идентификатор)

	sl = лямбда: сон (0,35)

	vk_session = vk_api. VkApi(токен=os.environ[«OLEG_VK_TOKEN»], captcha_handler=captchaHandler)
	попытка:
	vk_session.authorization()
	кроме vk_api.AuthorizationError как error_msg:
	печать (ошибка_сообщение)
	вк = vk_session.get_api()

	людей = список (карта (getUserId, sys.argv [1:]))
	fr = set(vk.friends.get(user_id=peoples[0])[‘items’])
	сл()
	для p в народах [1:]:
	fr = fr & set(vk. friends.get(user_id=p)[‘items’])
	сл()

	для мб во франц.:
	print(«http://vk.com/id{}».format(mb))

PYMK в ВК: ОД через ЭГО-СЕТИ. Возможность добавлять пользователей в друзья есть… | от команды ВК

Возможность добавлять пользователей в друзья — одна из важнейших механик любой социальной сети. Подавляющее большинство взаимодействий происходит между пользователями, которые дружат друг с другом. Они видят и комментируют сообщения друг друга в своих новостных лентах и заходят в свои списки друзей, чтобы начать чаты. Вот почему так важен рост социального графа.

Меня зовут Евгений Замятин. Я являюсь частью команды Core ML в ВКонтакте. Хочу рассказать вам о том, как работает наша рекомендательная система, чтобы сблизить пользователей крупнейшей социальной сети рунета.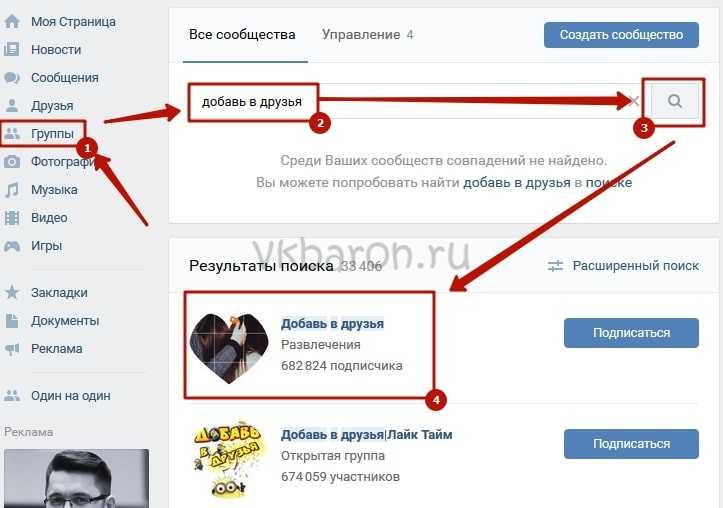

Современные рекомендательные системы часто состоят из двух уровней, и наша система не исключение.

Первый уровень — поисковая часть системы. Его задача — искать среди всего множества пользователей наиболее релевантных кандидатов. Этот процесс нужно сделать быстро. Обычно эти задачи решаются с помощью простых в использовании моделей, таких как матричные факторизации или эвристики, основанные на количестве общих друзей. Затем кандидаты, полученные на первом уровне, отправляются на второй уровень, где на модель больше не распространяются строгие ограничения скорости. Его основная задача — обеспечить максимальную точность предсказания и создать список, который увидит пользователь. В этой статье мы рассмотрим только первый этап — поиск.

Прежде всего сформулируем постановку задачи. Для каждого пользователя нам нужно найти k кандидатов, которых они с наибольшей вероятностью добавят в друзья. Метрика, на которой мы сосредоточимся, — это отзыв@k. Для этой задачи идеально подходит, так как нас интересует не порядок кандидатов, а важна их релевантность.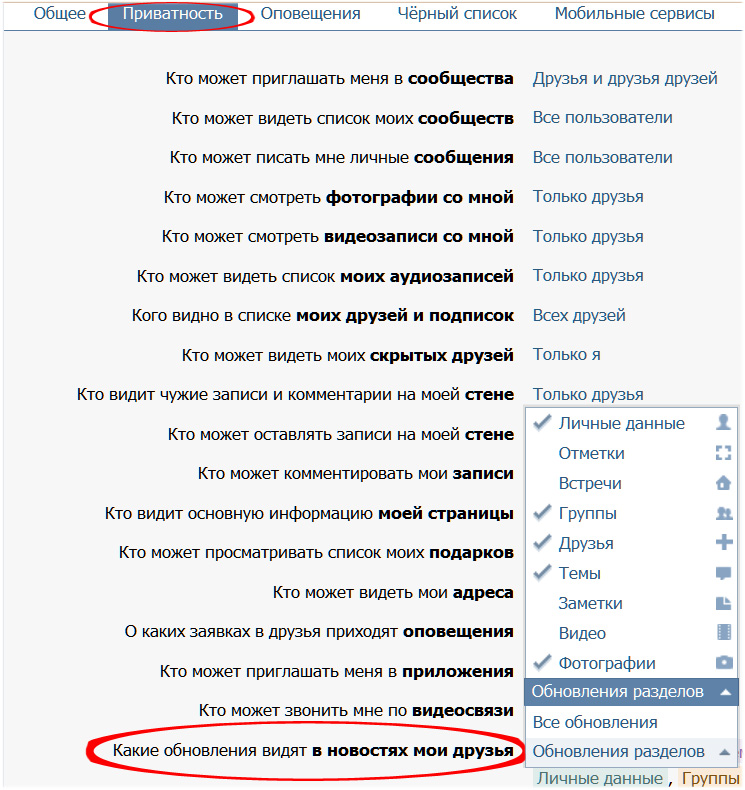

Давайте рассмотрим базовые, но до сих пор актуальные решения, придуманные десятки лет назад. Первый метод, который приходит на ум, самый логичный: эвристика, основанная на количестве общих друзей. Для каждого пользователя выбираются кандидаты с наибольшим значением. Этот подход прост в реализации и обеспечивает достойное качество результатов.

Еще одним важным методом рекомендации друзей является Adamic/Adar. Он также основан на анализе общих друзей, хотя и модифицированном: авторы предлагают учитывать количество друзей, которые есть у «общего» друга. Чем больше это значение, тем меньше релевантной информации оно несет.

Недавно наши коллеги из Google+ предложили новый подход к рекомендациям друзей, основанный на эго-сетях. В своей статье авторы предложили кластеризовать эго-сети пользователей. В качестве меры релевантности они использовали значение 9.0206 показатель дружбы , который представляет собой количество общих друзей в одном кластере эго-сетей.

Помимо методов, основанных на анализе общих друзей, довольно распространены рекомендации на основе встраивания. В Лаборатории искусственного интеллекта ВК МФТИ мы провели исследование, в котором сравнили эффективность разных подходов к задаче предсказания дружбы в ВК. Результаты совпали с нашим опытом. Решения, основанные на встраивании графов, нам не подходят. Помня об этом, мы начали разрабатывать систему отбора кандидатов на основе анализа общих друзей.

Общая схема нашего метода расширяет идеи числа общих друзей и Адамика/Адара. Конечная мера релевантности E(u, v) , с помощью которой мы будем отбирать кандидатов, также раскладывается на сумму общих друзей u и v . Ключевое отличие заключается в форме слагаемого под суммой. В нашем случае это мера ez_c(u, v)

Сначала попробуем понять «физический» смысл меры ez_c(u, v) . Представьте, что мы взяли пользователя c и спросили его: «Насколько вероятно, что два ваших друга, и и и , станут друзьями?» Чем больше информации этот пользователь учитывает для своего прогноза, тем точнее он будет. Например, если c может вспомнить только количество своих друзей, его рассуждения могут выглядеть так: «Чем больше у меня друзей, тем меньше вероятность того, что два случайных человека узнают друг друга». Тогда оценка «вероятности» дружбы u и v (с точки зрения c ) могут выглядеть как 1/log(n) , где n — количество друзей. Вот как работает Адамик/Адар. Но что, если c учитывает больше контекста?

Прежде чем ответить на этот вопрос, давайте разберемся, почему

ez_c(u, v) важно определить через пользователя c . Дело в том, что в таком виде очень удобно решать задачу распределённо. Представьте, что мы разослали всем пользователям платформы анкету с просьбой оценить вероятность того, что каждая пара их друзей дружит друг с другом. Получив все ответы, мы можем подставить значения в формулу Э(и,в) . Вот как выглядит вычисление E(u, v) с помощью MapReduce:

Подготовка . Для каждого c выделен контекст, который он будет учитывать для проведения оценок. Например, в Adamic/Adar это будет просто список друзей.
Карта . «Спросите» каждого c , что они думают о возможности дружбы для каждой пары своих друзей. Мы вычисляем ez_c(u, v) и сохраняем его как (u, v) → ez_c(u, v) для всех u , v в N(c) . В случае Адамика/Адара: (u, v) → 1 / log|N(c)| .
Уменьшить . Для каждой пары (u, v) суммируем все соответствующие значения. Их будет ровно столько, сколько общих друзей у и и и .

Таким образом, мы получаем все ненулевые значения E(u, v) . Примечание: необходимое условие для E(u, v) > 0 есть наличие хотя бы одного общего друга u и v .

Контекст пользователя c в случае меры ez_c будет тот же список друзей, но дополненный информацией об отношениях внутри этого списка. Научный термин для такой структуры — «эго-сеть». Более формально эго-сеть вершины x является подграфом исходного графа, все вершины которого являются соседями вершины x 9.0207 и x , ребра которого являются всеми ребрами исходного графа между этими вершинами.

Основная идея показателя ez_c заключается в том, что его можно сделать обучаемым. Для каждого пользователя с , его эго-сети и всех пар пользователей u, v внутри нее мы можем насчитать множество различных признаков. Например:

количество общих друзей u и v внутри эго-графа c
количество общих друзей u и c
интенсивность взаимодействия между v и c
время, прошедшее с момента последней дружбы между u и кем-то из эго-графа c
плотность графа эго c
и другие

Таким образом, мы получим набор данных с функциями. Но нам также нужны метки для обучения. Рассмотрим набор данных, построенный из состояния графа в момент времени T . Тогда в качестве положительных примеров возьмем те пары пользователей, которые не были друзьями на момент T , но подружились с T + △T . И как минус, все остальные пары пользователей, которые не являются друзьями. Примечание: поскольку мы решаем задачу прогнозирования новых дружеских отношений, те пары пользователей, которые уже являются друзьями в момент времени T , не нужно учитывать ни в обучении, ни на практике.

В итоге получаем следующий набор данных:

для каждой пары пользователей u и v , а также их общий друг c , характеристики рассчитываются внутри эго-сети c
пара пользователей u и v встречается в наборе данных ровно столько раз, сколько у них есть общие друзья
все пары пользователей в наборе данных не друзья во времени T
для каждой пары u и v метка равна 1, если они стали друзьями в течение времени △T начиная с T и 0 иначе

Мы будем использовать этот набор данных для обучения нашей меры ez_c . В качестве модели мы выбрали градиентный бустинг с функцией парных потерь, где ID группы — user u .

По существу, мера ez_c (u, v) определяется как предсказание модели, описанной выше. Но есть один нюанс: при парном обучении распределение предсказаний модели похоже на нормальное. Следовательно, если мы возьмем «сырой» прогноз в качестве определения меры ez_c(u, v) , у нас может возникнуть ситуация, когда мы оштрафуем окончательную меру E(u, v) для общих друзей, поскольку значения прогнозов отрицательны. Это не совсем понятно, так как мы не хотим, чтобы мера E(u, v) уменьшалась с увеличением числа общих друзей. Итак, в дополнение к предсказанию модели мы решили взять показатель степени:

Этот подход хорошо работает на небольших графиках. Но чтобы применить его к реальным данным, нам нужно выполнить еще одно действие. Суть проблемы такова: мы не можем рассчитать признаки и применить модель для каждой пары пользователей всех эго-сетей, так как это заняло бы слишком много времени. Чтобы решить эту проблему, мы придумали специальный трюк. Представим, что наше повышение градиента обучено так, что каждое дерево использует атрибуты только одного пользователя: либо и или и . Тогда мы могли бы разделить весь ансамбль на две группы: к группе A мы бы отнесли деревья, которые используют только атрибуты пользователя u , к B , пользователя v . Предсказание такой модели может быть представлено как:

С помощью такой модели мы могли бы быстрее получать предсказания для всех пар пользователей одной и той же эго-сети. Все, что нам нужно сделать, это применить модели A и B для каждого пользователя, а затем сложить прогнозы, соответствующие парам. Таким образом, для эго-сети из n вершин мы могли бы уменьшить количество применений модели с O(n²) до O(n) .

Но как нам получить модель, в которой каждое дерево зависит только от одного пользователя? Вот как:

Исключите из набора данных все признаки, которые одновременно зависят как от u , так и от v . Например, атрибут «количество общих друзей х и х внутри графа эго с» придется удалить.
Модель поезда A , использующая только функции, основанные на u , c и эго-сеть c .
Для обучения модели B оставьте только признаки, основанные на v , c и ego-net c . Передайте прогнозы модели A в качестве базовых прогнозов.

Если мы объединим модели A и B , мы получим то, что нам нужно: первая часть использует функции u , вторая использует функции v . Набор моделей имеет смысл, потому что B был обучен «исправлять» Предсказания A . Такая оптимизация позволяет ускорить расчеты в сотни раз и делает подход применимым на практике. Окончательный результат ez_c(u, v) и E(u, v) выглядит следующим образом:

Обратите внимание, что E(u, v) можно представить как:

Эта формула является скалярным произведением разреженных векторов, индексы которых являются пользователями, а значения — показателями прогнозов модели. Ненулевые значения здесь только для друзей u — по сути, это просто списки друзей с дополнительными значениями.

При построении рекомендаций мы уже рассчитали прогнозы модели для всех существующих дружеских отношений. Поэтому для каждого пользователя мы можем собрать векторы и поместить их в доступное онлайн-хранилище ключей-значений. После этого мы можем получить значение 90 206 E(u, v) 90 207 для любой пары пользователей онлайн с помощью простой операции умножения векторов. Это позволяет использовать E(u, v) в качестве легкой функции релевантности в высоконагруженных частях системы или в качестве дополнительного признака итоговой модели ранжирования.

В результате система EGOML позволяет:

Подбирать кандидатов для каждого пользователя офлайн в распределенных настройках. Асимптотическая сложность оптимизированного алгоритма составляет O(|E|) вычислений признаков и модельных приложений, где |E| — количество подключений в графе.

Как стать общим другом в вк: Как добавить в общие друзья ВКонтакте