Как узнать районный коэффициент: Районный коэффициент по регионам России в 2022 году — СКБ Контур
Районный коэффициент к заработной плате в 2023 году
Районный коэффициент — это специальный показатель, учитываемый при расчете заработной платы за труд в особых условиях. Он был установлен еще в СССР в качестве надбавки к оплате. Основная цель введения — привлечение работников в удаленные регионы.
Кем определяются коэффициенты
Коэффициенты устанавливаются Правительством России. Работодатели не вправе менять их, соответственно, они обязательны к применению. Перечень содержится в Постановлении Правительства РФ №1237 от 30.12.2011 года. Указание на обязательное применение коэффициента содержится и в Трудовом кодексе РФ (статьи 146, 315 и 316).
Размер коэффициентов
Размер зависит от региона, в котором трудится гражданин. Величина варьируется от 1.1 (например, в Калмыкии) и до 2 (отдельные районы Якутии, Командорские острова).
Чем более суровыми считаются условия труда, тем выше коэффициент. Его увеличение необходимо для привлечения и удержания сотрудников на особо важных предприятиях, для роста числа проживающих в отдельных местностях.
Его увеличение необходимо для привлечения и удержания сотрудников на особо важных предприятиях, для роста числа проживающих в отдельных местностях.
Обязан ли работодатель применять коэффициенты
Районный коэффициент считается составной частью заработной платы и неотделим от нее. При отказе от его начисления, работодатель несет такую же ответственность, как при невыплате заработной платы.
Таблица районных коэффициентов на 2022 год
| Субъект РФ | Районный коэффициент |
| Республика Алтай: | |
| на всей территории | 1,4 |
| Кош-Агачский, Улаганский районы | 1,4 |
| Республика Башкортостан: | |
| на всей территории | 1,15 |
| Республика Бурятия: | |
| на всей территории | 1,2 |
| Баргузинский, Курумканский, Окинский районы | 1,3 |
Баунтовский, Муйский, Северобайкальский районы, г. Северобайкальск Северобайкальск |
1,7 |
| Республика Дагестан: | |
| для населенных пунктов, находящихся на высоте от 2000 до 3000 метров над уровнем моря | 1,2 |
| для населенных пунктов, находящихся на высоте от 1500 до 2000 метров над уровнем моря | 1,15 |
| Республика Калмыкия: | |
| на территории Калмыцкой АССР, ограниченной с севера и запада линией границы с Астраханской областью через с. Чомпот, с. Северный, пос. Цаган-Нур, с. Буругсун — 10 км, восточнее с. Кугульты, далее до южной границы Приозерного района с. Шатта-УланЭрге, с. Ики-Бурул, пос. Южный, с юга по границе Калмыцкой АССР со Ставропольским краем и Дагестанской АССР до Каспийского моря; в совхозах «Раздольный», «Северный», им. Чкалова, «Новый», «Ялмата», «Улан-Эргинский», «Красный Путиловец», «Хомутниковский» | 1,3 |
на территории Юстинского, МалоДербетовского и Приозерного районов, ограниченной с запада линией от озера Барманнак, совхоз им. Чапаева, с. Деде-Ламон — с. Бургсун и с юга территорией, где предусмотрен коэффициент в размере 1,3; на территории Приозерного, Целинного, Яшкульского и Ики-Бурульского районов, ограниченный с запада и северо-запада линией 10 км восточнее Кегульты с. Бор-Нур, с. Джендик, пос. Буратинский, с. Гигант с юга и юго-востока границей Ики-Бурульского района со Ставропольским краем, с севера и востока — территории, где предусмотрен коэффициент 1,3; в совхозах «Буратинский», «Приозерный», «Бага-Бурульский», «Маныч» Чапаева, с. Деде-Ламон — с. Бургсун и с юга территорией, где предусмотрен коэффициент в размере 1,3; на территории Приозерного, Целинного, Яшкульского и Ики-Бурульского районов, ограниченный с запада и северо-запада линией 10 км восточнее Кегульты с. Бор-Нур, с. Джендик, пос. Буратинский, с. Гигант с юга и юго-востока границей Ики-Бурульского района со Ставропольским краем, с севера и востока — территории, где предусмотрен коэффициент 1,3; в совхозах «Буратинский», «Приозерный», «Бага-Бурульский», «Маныч» |
1,2 |
| на территории Калмыцкой АССР, за исключением территории, где предусмотрены коэффициенты 1,3 и 1,2, г. Элисты и территории западнее озера Маныч и МанычГудило; в совхозах «АршаньЗельменский», «Обильный», «Ергенинский», «Садовый», «Троицкий», «Балковский», «Западный», «Ленинский», «Вознесеновский» | 1,1 |
| в населенных пунктах, обеспеченных питьевой водой и водой для бытовых нужд, а также в районных центрах коэффициенты снижаются соответственно с 1,3 до 1,2, с 1,2 до 1,1 | |
| Республика Карелия: | |
| Кондопожский, Питкярантский, Прионежский, Пряжинский, Суоярвский, Лахденпохский, Олонецкий районы, города Петрозаводск, Сортавала | 1,15 |
| Медвежьегорский, Муезерский, Пудожский, Сегежский районы | 1,3 |
г. Сегежа и подчиненные его Администрации населенные пункты Сегежа и подчиненные его Администрации населенные пункты |
|
| Беломорский, Калевальский, Кемский, Лоухский районы, г. Костомукша | 1,4 |
| г. Кемь и подчиненные его Администрации населенные пункты | |
| Республика Коми: | |
| Княжногорский, Корткоросский, Сысольский, Сыктывдинский, Прилузский, Усть-Вымский, УстьКуломский, Койгородский районы, г. Сыктывкар | 1,2 |
| Печорский, Сосногорский, Ижемский, Усть-Цилемский, Троицко-Печорский, Удорский районы | 1,3 |
| города Ухта и подчиненные его Администрации населенные пункты, Печора и подчиненные его Администрации населенные пункты, Сосногорск и подчиненные его Администрации населенные пункты, Вуктыл и подчиненные его Администрации населенные пункты | |
| Вуктыльский район, г. Вуктыл | 1,4 |
| Усинский район, города Инта, Усинск | 1,5 |
г. Воркута Воркута |
1,6 |
| Республика Саха (Якутия): | |
| районы, расположенные до Полярного круга, южнее 65 град. северной широты: Алданский, Амгинский, Верхневилюйский, Вилюйский, Горный, Кобяйский, Ленинский, Ленский, МегиноКангаласский, Нерюнгринский, Намский, Мирнинский, Олекминский, Орджоникидзевский, Сунтарский, Таттинский, Томпонский, УстьАлданский, Усть-Майский, Чурапчинский, Якутский | 1,7 |
| районы, расположенные за Полярным кругом, не ниже 65° северной широты: Абыйский, Аллаиховский, Анабарский, Булунский, Верхнеколымский, Верхоянский, Жиганский, Мирнинский (территория Айхальского поссовета и Удачнинского горсовета), Момский, Нижнеколымский, Оймяконский, Оленекский, Среднеколымский, Усть-Янский, Эвено-Бытантайский | 2 |
| местности, где расположены предприятия и стройки алмазодобывающей промышленности, на месторождениях «Айхал» и «Удачная», прииски «Депутатский» и «Кулар» | 2 |
| Республика Тыва: | |
| на всей территории | 1,4 |
| Монгун-Тайгинский, Тожинский, Кызылский (территория Шынаанской сельской Администрации) районы | 1,5 |
| Удмуртская Республика | |
| на всей территории | 1,15 |
| Республика Хакасия: | |
| на всей территории | 1,3 |
| Алтайский край: | |
| на всей территории | 1,15 |
| Алейский, Баевский, Благовещенский, Бурлинский, Волчихинский, Егорьевский, Завьяловский, Ключевский, Кулундинский, Мамонтовский, Михайловский, Немецкий, Новичихинский, Панкрушихинский, Поспелихинский, Родинский, Романовский, Рубцовский, Славгородский, Суетский, Табунский, Угловский, Хабаровский, Шипуновский районы, города краевого подчинения Алейск, Славгород, Яровое | 1,25 |
| Красноярский край: | |
| на всей территории | 1,3 |
| Кежемский район | 1,6 |
Туруханский (севернее рек Нижняя Тунгуска и Турухан) район, местности, расположенные севернее Полярного круга (за исключением г. Норильска и подчиненных его Администрации населенных пунктов), г. Игарка и подчиненные его Администрации населенные пункты Норильска и подчиненных его Администрации населенных пунктов), г. Игарка и подчиненные его Администрации населенные пункты |
|
| г. Норильск и подчиненные его Администрации населенные пункты | 1,8 |
| Приморский край: | |
| на всей территории | 1,3 |
| поселки рудников Таежный и Тернистый Красноармейского района | 1,4 |
| Хабаровский край: | |
| Хабаровский, Бикинский, Вяземский, имени Лазо, Нанайский районы, г. Хабаровск | 1,3 |
| Аяно-Майский, Тугуро-Чумиканский, Николаевский, имени Полины Осипенко, Комсомольский, Советско-Гаванский, Ванинский, Солнечный, Амурский, Верхнебуреинский, Ульчский районы, г. Комсомольск-на-Амуре | 1,5 |
| Охотский район | 1,7 |
| Амурская область: | |
| Архаринский, Белогорский, Благовещенский, Бурейский, Завитинский, Ивановский, Константиновский, Мазановский, Михайловский, Октябрьский, Ромненский, Свободненский, Серышевский, Тамбовский районы, города Благовещенск, Белогорск, Райчихинск, Свободный | 1,3 |
Магдачинский, Шимановский районы, г.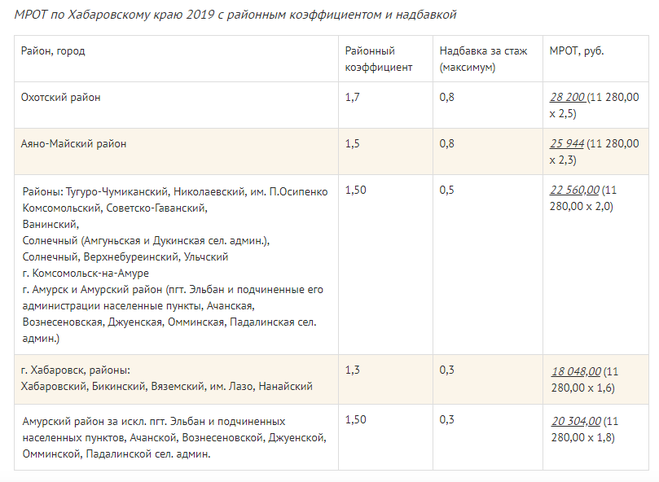 Шимановск Шимановск |
1,4 |
| Сковородинский район | 1,5 |
| Зейский, Селемджинский, Тындинский районы, города Зея, Тында | 1,7 |
| Архангельская область: | |
| на всей территории | 1,2 |
| Лешуковский, Пинежский районы | 1,4 |
| Мезенский, Соловецкий районы, г. Северодвинск и подчиненные его Администрации населенные пункты | 1,7 |
| Астраханская область: | |
| районный коэффициент применяется к заработной плате работников предприятий и организаций, находящихся в пустынных и безводных районах на «черных землях», «кизлярских пастбищах», на части Лиманского района | 1,1 |
| районный коэффициент применяется к заработной плате работников за работу в пустынных и безводных районах, занятых на водохозяйственном строительстве и на строительстве объектов в совхозах и других сельскохозяйственных предприятиях Астраханской области | 1,35 |
| районный коэффициент применяется к заработной плате за работу в пустынной и безводной местности: работников, занятых на геологоразведочных работах, бурении скважин, строительстве и эксплуатации объектов Астраханского газоконденсатного месторождения, включая работников подсобно-вспомогательных предприятий, баз строительной индустрии, а также работников МВД СССР, занятых на этом строительстве; работников предприятий и организаций, обслуживающих строительство и эксплуатацию Астраханского газоконденсатного месторождения; работников и служащих предприятий, организаций, учреждений, расположенных в населенных пунктах в восьмикилометровой санитарнозащитной зоне Астраханского газового комплекса на период до переселения последних с этой территории | |
| Вологодская область: | |
Бабаевский, Вологодский, Грязовецкий, Кадуйский, Междуреченский, Сокольский, Устюженский, Чагодощенский, Череповецкий, Шекснинский районы, г. Вологда Вологда |
1,15 |
| г. Череповец с территорией, подчиненной городскому Совету народных депутатов | 1,25 |
| Иркутская область: | |
| на всей территории (за исключением г. Ангарска, г. Черемхово и Черемховского р-на, г. Тулуна и Тулунского р-на и работников ВСЖД, по которым приняты решения облисполкома и постановления Главы Администрации) | 1,3 |
| Братский район, г. Братск | 1,4 |
| Усть-Илимский, Нижнеилимский районы, г. Усть-Илимск | 1,6 |
| Усть-Кутский район | 1,7 |
| Камчатская область: | |
| на всей территории | 1,8 |
| Командорские острова | 2 |
| Кемеровская область: | |
| на всей территории | 1,3 |
| Кировская область: | |
Афанасьевский, Белохолуницкий, Богородский, Верхнекамский, Даровский, Зуевский, КировоЧепецкий, Каменский, Лузский, Мурашинский, Омутнинский, Нагорский, Опаринский, Подосиновский, Слободской, Унинский, Феленский, Халтуринский, Юрьянский районы, г. Киров с территорией, подчиненной городскому Совету народных депутатов Киров с территорией, подчиненной городскому Совету народных депутатов |
1,15 |
| Костромская область: | |
| Буйский, Галичский, Солигаличский, Чухломский, Судайский, Нейский, Мантуровский, Кологривский, Межевский, Шарьинский, Поназыревский, Вохомский, Пыщугский, Павинский, Парфеньевский районы (районный коэффициент применяется к заработной плате работников лесозаготовительных, лесосплавных, лесоперевалочных предприятий, организаций и химлесхозов) | 1,15 |
| Курганская область: | |
| на всей территории | 1,15 |
| Магаданская область: | |
| на всей территории | 1,7 |
| Мурманская область: | |
| на всей территории | 1,5 |
| пгт. Туманный | 1,7 |
| Мурманск-140 | 1,8 |
| Новосибирская область: | |
| на всей территории | 1,25 |
| Омская область: | |
| на всей территории | 1,15 |
| Оренбургская область: | |
| на всей территории | 1,15 |
| Пермская область: | |
| на всей территории | 1,15 |
| Красновишерский, Чердынский районы | 1,2 |
| Ростовская область: | |
Заветинский, Ремонтненский районы; Дубовский, Зимовниковский, Орловский, Пролетарский районы, ограниченные с запада линией железной дороги Сальск — Волгоград, с севера границей с Волгоградской областью, с востока, северовостока и юга — границей с Республикой Калмыкия (в районных центрах с. Дубовское, пос. Зимовники, пос. Орловский и г. Пролетарск коэффициент не применяется) Дубовское, пос. Зимовники, пос. Орловский и г. Пролетарск коэффициент не применяется) |
1,1 |
| Сахалинская область: | |
| Александровск-Сахалинский, Анивский, Долинский, Корсаковский, Макаровский, Невельский, Поронайский, Смирныховский, Томаринский, Тымовский, Углегорский, Холмский районы, г. Южно-Сахалинск | 1,6 |
| Ногликский, Охинский районы | 1,8 |
| Курильский, Северо-Курильский и Южно-Курильский районы | 2 |
| Свердловская область: | |
| на всей территории | 1,15 |
| Гаринский, Таборинский районы, на территориях, находящихся в Административном подчинении Ивдельского, Карпинского, Краснотурьинского и Североуральского горсоветов (включая города) | 1,2 |
| Томская область: | |
| Бакчарский, Кривошеинский, Молчановский, Тегульдетский районы | 1,3 |
| Александровский, Верхнекетский, Каргасокский, Колпашевский, Парабельский, Чаинский районы, города Кедровый, Колпашево, Стрежевой | 1,5 |
| районный коэффициент применяется к заработной плате работников предприятий и организаций, занятых в нефтяной, газовой промышленности, на геологических и топографо-геодезических работах, а также работников строительных, строительномонтажных и специализированных управлений, подсобновспомогательных производств, транспорта, хозяйств и организаций, обслуживающих нефтегазодобывающие предприятия, конторы бурения, строительство объектов нефтяной и газовой промышленности, геологические и топографо-геодезические работы на территории Томской области севернее 60° северной широты | 1,7 |
| Тюменская область: | |
| на всей территории | 1,15 |
| Уватский район | 1,5 |
Тобольский, Вагайский районы, г. Тобольск (только для работников бюджетной сферы) Тобольск (только для работников бюджетной сферы) |
1,217 |
| Челябинская область: | |
| на всей территории | 1,15 |
| Читинская область: | |
| на всей территории | 1,4 |
| Тунгокоченский, Чернышевский, Тунгиро-Олекминский, Могочинский районы | 1,5 |
| Каларский район | 1,7 |
| Еврейская автономная область: | |
| на всей территории | 1,3 |
| Агинский Бурятский автономный округ: | |
| на всей территории | 1,4 |
| Коми-Пермяцкий автономный округ: | |
| на всей территории | 1,15 |
| Гайнинский район | 1,2 |
| Кочевской, Косинский районы | 1,2 |
| Корякский автономный округ: | |
| на всей территории | 1,6 |
| на всей территории (районный коэффициент применяется к заработной плате работников строительных и ремонтностроительных организаций) | 1,8 |
| на всей территории (районный коэффициент применяется к заработной плате работников лесного хозяйства) | 2 |
| Ненецкий автономный округ: | |
| на всей территории | 1,8 |
| Таймырский (Долгано-Ненецкий) автономный округ: | |
| на всей территории | 1,8 |
| Усть-Ордынский Бурятский автономный округ: | |
| на всей территории | 1,3 |
| Ханты-Мансийский автономный округ — Югра: | |
| на всей территории | 1,7 |
| Чукотский автономный округ: | |
| на всей территории | 2 |
| Эвенкийский автономный округ: | |
| Байкитский, Тунгусско-Чунский районы | 1,5 |
| Илимпийский район | 1,6 |
| Ямало-Ненецкий автономный округ: | |
| севернее Полярного круга (66° 33,3′ северной широты): | 1,8 |
г. Салехард, Аксарковский сельсовет Приуральского района Салехард, Аксарковский сельсовет Приуральского района |
|
| г. Лабытнанги, с. Сидоровск Красноселькупского района, Ныдинский и Ямбургский сельсоветы Ныдымского района, Байдарацкий, Белоярский и Харсаимский сельсоветы Приуральского района, Самбургский сельсовет Пуровского района, Тазовский, Ямальский районы | |
| южнее Полярного круга (66° 33,3′ северной широты): г. Губкинский, г. Муравленко, г. Надым, г. Новый Уренгой, г. Ноябрьск, Красноселькупский район (за исключением с. Сидоровск), Надымский район (за исключением Ныдинского и Ямбургского сельсоветов), Зеленоярский и Катравожский сельсоветы Приуральского района, Пуровский район (за исключением Самбургского сельсовета), Шурышкарский район |
Получить юридическую помощь по вопросам районного коэффициента к заработной плате можно на нашем сайте.
Территориальные коэффициенты ОСАГО — 2022 для всех российских регионов и городов
Российский Центробанк в сентябре 2022 года изменил территориальные коэффициенты ОСАГО для легковых автомобилей. Mafin Media публикует полный список обновленных показателей для всей России.
Mafin Media публикует полный список обновленных показателей для всей России.
Территория преимущественного использования авто | Коэффициент | |
| 1 | Республика Адыгея (Адыгея) | 1,24 |
| 2 | Республика Алтай | |
| 2.1 | Горно-Алтайск | 1,24 |
| 2.2 | Прочие города и населенные пункты | 0,76 |
| 3 | Республика Башкортостан | |
| 3.1 | Благовещенск, Октябрьский | 1,16 |
| 3.2 | Ишимбай, Кумертау, Салават | 1,08 |
| 3.3 | Стерлитамак, Туймазы | 1,24 |
| 3.4 | Уфа | 1,64 |
| 3.5 | Прочие города и населенные пункты | 1 |
| 4 | Республика Бурятия | |
4. 1 1 | Улан-Удэ | 1,24 |
| 4.2 | Прочие города и населенные пункты | 0,76 |
| 5 | Республика Дагестан | |
| 5.1 | Буйнакск, Дербент, Каспийск, Махачкала, Хасавюрт | 0,96 |
| 5.2 | Прочие города и населенные пункты | 0,9 |
| 6 | Республика Ингушетия | |
| 6.1 | Малгобек | 0,94 |
| 6.2 | Назрань | 0,82 |
| 6.3 | Прочие города и населенные пункты | 0,82 |
| 7 | Кабардино-Балкарская Республика | |
| 7.1 | Нальчик, Прохладный | 1 |
| 7.2 | Прочие города и населенные пункты | 0,88 |
| 8 | Республика Калмыкия | |
| 8.1 | Элиста | 1,24 |
| 8.2 | Прочие города и населенные пункты | 0,82 |
| 9 | Карачаево-Черкесская Республика | 1 |
| 10 | Республика Карелия | |
10. 1 1 | Петрозаводск | 1,24 |
| 10.2 | Прочие города и населенные пункты | 0,84 |
| 11 | Республика Коми | |
| 11.1 | Сыктывкар | 1,48 |
| 11.2 | Ухта | 1,24 |
| 11.3 | Прочие города и населенные пункты | 1 |
| 12 | Республика Крым | |
| 12.1 | Симферополь | 0,76 |
| 12.2 | Прочие города и населенные пункты | 0,68 |
| 13 | Республика Марий Эл | |
| 13.1 | Волжск | 1 |
| 13.2 | Йошкар-Ола | 1,32 |
| 13.3 | Прочие города и населенные пункты | 0,76 |
| 14 | Республика Мордовия | |
| 14.1 | Рузаевка | 1,16 |
| 14.2 | Саранск | 1,4 |
14. 3 3 | Прочие города и населенные пункты | 0,84 |
| 15 | Республика Саха (Якутия) | |
| 15.1 | Нерюнгри | 0,84 |
| 15.2 | Якутск | 1,16 |
| 15.3 | Прочие города и населенные пункты | 0,68 |
| 16 | Республика Северная Осетия — Алания | |
| 16.1 | Владикавказ | 1 |
| 16.2 | Прочие города и населенные пункты | 0,94 |
| 17 | Республика Татарстан (Татарстан) | |
| 17.1 | Альметьевск, Зеленодольск, Нижнекамск | 1,24 |
| 17.2 | Бугульма, Лениногорск, Чистополь | 1 |
| 17.3 | Елабуга | 1,16 |
| 17.4 | Казань | 1,8 |
| 17.5 | Набережные Челны | 1,56 |
17. 6 6 | Прочие города и населенные пункты | 1,08 |
| 18 | Республика Тыва | |
| 18.1 | Кызыл | 0,82 |
| 18.2 | Прочие города и населенные пункты | 0,82 |
| 19 | Удмуртская Республика | |
| 19.1 | Воткинск | 1,08 |
| 19.2 | Глазов, Сарапул | 1 |
| 19.3 | Ижевск | 1,48 |
| 19.4 | Прочие города и населенные пункты | 0,84 |
| 20 | Республика Хакасия | |
| 20.1 | Абакан, Саяногорск, Черногорск | 1 |
| 20.2 | Прочие города и населенные пункты | 0,82 |
| 21 | Чеченская Республика | 0,82 |
| 22 | Чувашская Республика — Чувашия | |
| 22.1 | Канаш | 1,08 |
22. 2 2 | Новочебоксарск | 1,16 |
| 22.3 | Чебоксары | 1,56 |
| 22.4 | Прочие города и населенные пункты | 0,88 |
| 23 | Алтайский край | |
| 23.1 | Барнаул | 1,56 |
| 23.2 | Бийск | 1,16 |
| 23.3 | Заринск, Новоалтайск, Рубцовск | 1,08 |
| 23.4 | Прочие города и населенные пункты | 0,76 |
| 24 | Забайкальский край | |
| 24.1 | Краснокаменск | 0,82 |
| 24.2 | Чита | 0,82 |
| 24.3 | Прочие города и населенные пункты | 0,68 |
| 25 | Камчатский край | |
| 25.1 | Петропавловск-Камчатский | 1,24 |
| 25.2 | Прочие города и населенные пункты | 1 |
| 26 | Краснодарский край | |
26. 1 1 | Анапа, Геленджик | 1,24 |
| 26.2 | Армавир, Сочи, Туапсе | 1,16 |
| 26.3 | Белореченск, Ейск, Кропоткин, Крымск, Курганинск, Лабинск, Славянск-на-Кубани, Тимашевск, Тихорецк | 1,08 |
| 26.4 | Краснодар, Новороссийск | 1,64 |
| 26.5 | Прочие города и населенные пункты | 1 |
| 27 | Красноярский край | |
| 27.1 | Ачинск, Зеленогорск | 1,08 |
| 27.2 | Железногорск, Норильск | 1,24 |
| 27.3 | Канск, Лесосибирск, Минусинск, Назарово | 1 |
| 27.4 | Красноярск | 1,64 |
| 27.5 | Прочие города и населенные пункты | 0,92 |
| 28 | Пермский край | |
| 28.1 | Березники, Краснокамск | 1,24 |
28. 2 2 | Лысьва, Чайковский | 1 |
| 28.3 | Пермь | 1,8 |
| 28.4 | Соликамск | 1,16 |
| 28.5 | Прочие города и населенные пункты | 1,08 |
| 29 | Приморский край | |
| 29.1 | Арсеньев, Артем, Находка, Спасск-Дальний, Уссурийск | 1 |
| 29.2 | Владивосток | 1,36 |
| 29.3 | Прочие города и населенные пункты | 0,96 |
| 30 | Ставропольский край | |
| 30.1 | Буденновск, Георгиевск, Ессентуки, Минеральные Воды, Невинномысск, Пятигорск | 1 |
| 30.2 | Кисловодск, Михайловск, Ставрополь | 1,16 |
| 30.3 | Прочие города и населенные пункты | 0,76 |
| 31 | Хабаровский край | |
| 31.1 | Амурск | 1 |
31. 2 2 | Комсомольск-на-Амуре | 1,27 |
| 31.3 | Хабаровск | 1,56 |
| 31.4 | Прочие города и населенные пункты | 0,88 |
| 32 | Амурская область | |
| 32.1 | Белогорск, Свободный | 1,08 |
| 32.2 | Благовещенск | 1,48 |
| 32.3 | Прочие города и населенные пункты | 1 |
| 33 | Архангельская область | |
| 33.1 | Архангельск | 1,64 |
| 33.2 | Котлас | 1,48 |
| 33.3 | Северодвинск | 1,56 |
| 33.4 | Прочие города и населенные пункты | 0,88 |
| 34 | Астраханская область | |
| 34.1 | Астрахань | 1,32 |
| 34.2 | Прочие города и населенные пункты | 0,84 |
| 35 | Белгородская область | |
35. 1 1 | Белгород | 1,24 |
| 35.2 | Губкин, Старый Оскол | 1 |
| 35.3 | Прочие города и населенные пункты | 0,84 |
| 36 | Брянская область | |
| 36.1 | Брянск | 1,4 |
| 36.2 | Клинцы | 1 |
| 36.3 | Прочие города и населенные пункты | 0,76 |
| 37 | Владимирская область | |
| 37.1 | Владимир | 1,48 |
| 37.2 | Гусь-Хрустальный | 1,08 |
| 37.3 | Муром | 1,16 |
| 37.4 | Прочие города и населенные пункты | 1 |
| 38 | Волгоградская область | |
| 38.1 | Волгоград | 1,24 |
| 38.2 | Волжский | 1,08 |
| 38.3 | Камышин, Михайловка | 1 |
38. 4 4 | Прочие города и населенные пункты | 0,76 |
| 39 | Вологодская область | |
| 39.1 | Вологда | 1,56 |
| 39.2 | Череповец | 1,64 |
| 39.3 | Прочие города и населенные пункты | 0,92 |
| 40 | Воронежская область | |
| 40.1 | Борисоглебск, Лиски, Россошь | 1,08 |
| 40.2 | Воронеж | 1,4 |
| 40.3 | Прочие города и населенные пункты | 0,84 |
| 41 | Ивановская область | |
| 41.1 | Иваново | 1,64 |
| 41.2 | Кинешма | 1,08 |
| 41.3 | Шуя | 1 |
| 41.4 | Прочие города и населенные пункты | 0,92 |
| 42 | Иркутская область | |
42. 1 1 | Ангарск | 1,16 |
| 42.2 | Братск, Тулун, Усть-Илимск, Усть-Кут, Черемхово | 1 |
| 42.3 | Иркутск | 1,56 |
| 42.4 | Усолье-Сибирское | 1,08 |
| 42.5 | Шелехов | 1,24 |
| 42.6 | Прочие города и населенные пункты | 0,84 |
| 43 | Калининградская область | |
| 43.1 | Калининград | 1,08 |
| 43.2 | Прочие города и населенные пункты | 0,84 |
| 44 | Калужская область | |
| 44.1 | Калуга | 1,16 |
| 44.2 | Обнинск | 1,24 |
| 44.3 | Прочие города и населенные пункты | 0,92 |
| 45 | Кемеровская область — Кузбасс | |
| 45.1 | Анжеро-Судженск, Киселевск, Юрга | 1,16 |
45. 2 2 | Белово, Березовский, Междуреченск, Осинники, Прокопьевск | 1,24 |
| 45.3 | Кемерово | 1,72 |
| 45.4 | Новокузнецк | 1,64 |
| 45.5 | Прочие города и населенные пункты | 1,08 |
| 46 | Кировская область | |
| 46.1 | Киров | 1,32 |
| 46.2 | Кирово-Чепецк | 1,16 |
| 46.3 | Прочие города и населенные пункты | 0,84 |
| 47 | Костромская область | |
| 47.1 | Кострома | 1,24 |
| 47.2 | Прочие города и населенные пункты | 0,76 |
| 48 | Курганская область | |
| 48.1 | Курган | 1,32 |
| 48.2 | Шадринск | 1,08 |
| 48.3 | Прочие города и населенные пункты | 0,76 |
| 49 | Курская область | |
49. 1 1 | Железногорск | 1 |
| 49.2 | Курск | 1,16 |
| 49.3 | Прочие города и населенные пункты | 0,76 |
| 50 | Ленинградская область | 1,24 |
| 51 | Липецкая область | |
| 51.1 | Елец | 1 |
| 51.2 | Липецк | 1,4 |
| 51.3 | Прочие города и населенные пункты | 0,84 |
| 52 | Магаданская область | |
| 52.1 | Магадан | 0,82 |
| 52.2 | Прочие города и населенные пункты | 0,76 |
| 53 | Московская область | 1,56 |
| 54 | Мурманская область | |
| 54.1 | Апатиты, Мончегорск | 1,24 |
| 54.2 | Мурманск | 1,88 |
| 54.3 | Североморск | 1,48 |
54. 4 4 | Прочие города и населенные пункты | 1,16 |
| 55 | Нижегородская область | |
| 55.1 | Арзамас, Выкса, Саров | 1,08 |
| 55.2 | Балахна, Бор, Дзержинск | 1,24 |
| 55.3 | Кстово | 1,16 |
| 55.4 | Нижний Новгород | 1,64 |
| 55.5 | Прочие города и населенные пункты | 1 |
| 56 | Новгородская область | |
| 56.1 | Боровичи | 1 |
| 56.2 | Великий Новгород | 1,24 |
| 56.3 | Прочие города и населенные пункты | 0,92 |
| 57 | Новосибирская область | |
| 57.1 | Бердск | 1,24 |
| 57.2 | Искитим | 1,16 |
| 57.3 | Куйбышев | 1 |
57. 4 4 | Новосибирск | 1,63 |
| 57.5 | Прочие города и населенные пункты | 1 |
| 58 | Омская область | |
| 58.1 | Омск | 1,48 |
| 58.2 | Прочие города и населенные пункты | 0,92 |
| 59 | Оренбургская область | |
| 59.1 | Бугуруслан, Бузулук, Новотроицк | 1 |
| 59.2 | Оренбург | 1,56 |
| 59.3 | Орск | 1,08 |
| 59.4 | Прочие города и населенные пункты | 0,84 |
| 60 | Орловская область | |
| 60.1 | Ливны, Мценск | 1 |
| 60.2 | Орел | 1,16 |
| 60.3 | Прочие города и населенные пункты | 0,76 |
| 61 | Пензенская область | |
61. 1 1 | Заречный | 1,16 |
| 61.2 | Кузнецк | 1 |
| 61.3 | Пенза | 1,32 |
| 61.4 | Прочие города и населенные пункты | 0,76 |
| 62 | Псковская область | |
| 62.1 | Великие Луки | 1 |
| 62.2 | Псков | 1,16 |
| 62.3 | Прочие города и населенные пункты | 0,76 |
| 63 | Ростовская область | |
| 63.1 | Азов | 1,16 |
| 63.2 | Батайск | 1,24 |
| 63.3 | Волгодонск, Гуково, Каменск-Шахтинский, Новочеркасск, Новошахтинск, Сальск, Таганрог | 1 |
| 63.4 | Ростов-на-Дону | 1,64 |
| 63.5 | Шахты | 1,08 |
| 63.6 | Прочие города и населенные пункты | 0,84 |
| 64 | Рязанская область | |
64. 1 1 | Рязань | 1,32 |
| 64.2 | Прочие города и населенные пункты | 0,92 |
| 65 | Самарская область | |
| 65.1 | Новокуйбышевск, Сызрань | 1,08 |
| 65.2 | Самара | 1,48 |
| 65.3 | Тольятти | 1,4 |
| 65.4 | Чапаевск | 1,16 |
| 65.5 | Прочие города и населенные пункты | 0,92 |
| 66 | Саратовская область | |
| 66.1 | Балаково, Балашов, Вольск | 1 |
| 66.2 | Саратов | 1,48 |
| 66.3 | Энгельс | 1,16 |
| 66.4 | Прочие города и населенные пункты | 0,76 |
| 67 | Сахалинская область | |
| 67.1 | Южно-Сахалинск | 1,4 |
| 67.2 | Прочие города и населенные пункты | 0,92 |
| 68 | Свердловская область | |
68. 1 1 | Асбест, Ревда | 1,08 |
| 68.2 | Березовский, Верхняя Пышма, Новоуральск, Первоуральск | 1,24 |
| 68.3 | Верхняя Салда, Полевской | 1,16 |
| 68.4 | Екатеринбург | 1,64 |
| 68.5 | Прочие города и населенные пункты | 1 |
| 69 | Смоленская область | |
| 69.1 | Вязьма, Рославль, Сафоново, Ярцево | 1 |
| 69.2 | Смоленск | 1,16 |
| 69.3 | Прочие города и населенные пункты | 0,76 |
| 70 | Тамбовская область | |
| 70.1 | Мичуринск | 1 |
| 70.2 | Тамбов | 1,16 |
| 70.3 | Прочие города и населенные пункты | 0,84 |
| 71 | Тверская область | |
| 71.1 | Вышний Волочек, Кимры, Ржев | 1 |
71. 2 2 | Тверь | 1,4 |
| 71.3 | Прочие города и населенные пункты | 0,84 |
| 72 | Томская область | |
| 72.1 | Северск | 1,16 |
| 72.2 | Томск | 1,48 |
| 72.3 | Прочие города и населенные пункты | 0,92 |
| 73 | Тульская область | |
| 73.1 | Алексин, Ефремов, Новомосковск | 1 |
| 73.2 | Тула | 1,4 |
| 73.3 | Узловая, Щекино | 1,16 |
| 73.4 | Прочие города и населенные пункты | 0,92 |
| 74 | Тюменская область | |
| 74.1 | Тобольск | 1,24 |
| 74.2 | Тюмень | 1,8 |
| 74.3 | Прочие города и населенные пункты | 1,08 |
| 75 | Ульяновская область | |
75. 1 1 | Димитровград | 1,16 |
| 75.2 | Ульяновск | 1,4 |
| 75.3 | Прочие города и населенные пункты | 0,92 |
| 76 | Челябинская область | |
| 76.1 | Златоуст, Миасс | 1,32 |
| 76.2 | Копейск | 1,48 |
| 76.3 | Магнитогорск | 1,64 |
| 76.4 | Сатка, Чебаркуль | 1,16 |
| 76.5 | Челябинск | 1,88 |
| 76.6 | Прочие города и населенные пункты | 1 |
| 77 | Ярославская область | |
| 77.1 | Ярославль | 1,4 |
| 77.2 | Прочие города и населенные пункты | 0,92 |
| 78 | Москва | 1,8 |
| 79 | Санкт-Петербург | 1,64 |
| 80 | Севастополь | 0,82 |
| 81 | Еврейская автономная область | |
81. 1 1 | Биробиджан | 0,82 |
| 81.2 | Прочие города и населенные пункты | 0,82 |
| 82 | Ненецкий автономный округ | 0,84 |
| 83 | Ханты-Мансийский автономный округ — Югра | |
| 83.1 | Когалым | 1 |
| 83.2 | Нефтеюганск, Нягань | 1,24 |
| 83.3 | Сургут | 1,8 |
| 83.4 | Нижневартовск | 1,64 |
| 83.5 | Ханты-Мансийск | 1,4 |
| 83.6 | Прочие города и населенные пункты | 1,08 |
| 84 | Чукотский автономный округ | 0,76 |
| 85 | Ямало-Ненецкий автономный округ | |
| 85.1 | Новый Уренгой | 1 |
| 85.2 | Ноябрьск | 1,56 |
| 85.3 | Прочие города и населенные пункты | 1,08 |
| 86 | Байконур | 0,82 |
4.
 2 Оценка коэффициентов модели линейной регрессии
2 Оценка коэффициентов модели линейной регрессииЭта книга находится в Open Review . Мы хотим, чтобы ваши отзывы сделали книгу лучше для вас и других учащихся. Вы можете аннотировать некоторый текст, выбрав его курсором, а затем щелкнув во всплывающем меню. Вы также можете увидеть аннотации других: нажмите в правом верхнем углу страницы
На практике точка пересечения \(\beta_0\) и наклон \(\beta_1\) линии регрессии совокупности неизвестны. Следовательно, мы должны использовать данные для оценки обоих неизвестных параметров. Далее будет использован пример из реальной жизни, чтобы продемонстрировать, как это достигается. Мы хотим связать результаты тестов с соотношением учеников и учителей, измеренным в калифорнийских школах. Результатом теста является средний балл по округу по чтению и математике для пятиклассников. Опять же, размер класса измеряется как количество учеников, деленное на количество учителей (соотношение учеников и учителей). Что касается данных, набор данных Калифорнийской школы (CASchools) поставляется с пакетом R под названием AER, аббревиатурой от Applied Econometrics with R (Christian Kleiber and Zeileis, 2020). После установки пакета с помощью install.packages («AER») и присоединения его с помощью библиотеки (AER) набор данных можно загрузить с помощью функции data().
Что касается данных, набор данных Калифорнийской школы (CASchools) поставляется с пакетом R под названием AER, аббревиатурой от Applied Econometrics with R (Christian Kleiber and Zeileis, 2020). После установки пакета с помощью install.packages («AER») и присоединения его с помощью библиотеки (AER) набор данных можно загрузить с помощью функции data().
## # установить пакет AER (один раз)
## install.packages("AER")
##
## # загрузить пакет AER
библиотека (АЕР)
# загрузить набор данных в рабочую область
data(CASchools) После того, как пакет был установлен, он доступен для использования в дальнейшем при вызове с помощью library() — нет необходимости снова запускать install.packages()!
Интересно узнать, с каким объектом мы имеем дело. class() возвращает класс объекта. В зависимости от класса объекта некоторые функции (например, plot() и summary()) ведут себя по-разному.
Проверим класс объекта CASchools.
класс (CASchools) #> [1] "data.frame"
Оказывается, CASchools относится к классу data. frame, с которым удобно работать, особенно для выполнения регрессионного анализа.
frame, с которым удобно работать, особенно для выполнения регрессионного анализа.
С помощью head() мы получаем первый обзор наших данных. Эта функция показывает только первые 6 строк набора данных, что предотвращает переполнение вывода консоли.
Нажмите ctrl + L, чтобы очистить консоль. Эта команда удаляет любой код, который был введен и выполнен вами или напечатан на консоли с помощью функций R. Хорошая новость в том, что все остальное осталось нетронутым. Вы не теряете ни определенные переменные и т. д., ни историю кода. По-прежнему можно вызвать ранее выполненные команды R с помощью клавиш вверх и вниз. Если вы работаете в RStudio , нажмите ctrl + Up на клавиатуре (CMD + Up на Mac), чтобы просмотреть список ранее введенных команд.
голова (CASchools) #> районная школа округа классы ученики учителя кальворкс обед компьютер расходы доход #> 1 75119 Sunol Glen Unified Alameda KK-08 195 10,90 0,5102 2,0408 67 6384,911 22,6 #> 2 61499 Мансанита Элементарная школа KK-08 240 11,15 15,4167 47,9167 101 5099,381 9,824000 #> 3 61549 Thermalito Union Elementary Butte KK-08 1550 82,90 55,0323 76,3226 169 5501,955 8,978000 #> 4 61457 Golden Feather Union Elementary Butte KK-08 243 14,00 36,4754 77,0492 85 7101,831 8,978000 #> 5 61523 Элементарная школа Палермо Юнион КК-08 1335 71,50 33,1086 78,4270 171 5235,988 9,080333 #> 6 62042 Burrel Union Elementary Fresno KK-08 137 6,40 12,3188 86,9565 25 5580,147 10,415000 #> английский читать математику #> 1 0,000000 691,6 690,0 #> 2 4,583333 660,5 661,9 #> 3 30.000002 636,3 650,9 #> 4 0,000000 651,9 643,5 #> 5 13,857677 641,8 639,9 #> 6 12.408759 605.7 605.4
Мы обнаружили, что набор данных состоит из множества переменных, и большинство из них являются числовыми.
Кстати: альтернативой class() и head() является str(), которая выводится из «структуры» и дает исчерпывающий обзор объекта. Пытаться!
Возвращаясь к CASchools, две интересующие нас переменные (т. е. средний балл за тест и соотношение учеников и учителей) включают , а не . Однако по предоставленным данным можно рассчитать и то, и другое. Чтобы получить соотношение учеников и учителей, мы просто делим количество учеников на количество учителей. Средний балл за тест представляет собой среднее арифметическое балла за тест по чтению и балла за тест по математике. Следующий фрагмент кода показывает, как две переменные могут быть сконструированы как векторы и как они присоединяются к CASchools.
# вычислить STR и добавить его в CASchools CASchools$STR <- CASchools$студенты/CASchools$учителя # вычислить TestScore и добавить его в CASchools CASchools$score <- (CASchools$read + CASchools$math)/2
Если мы снова запустим head(CASchools), то обнаружим две интересующие нас переменные в виде дополнительных столбцов с именами STR и score (проверьте это!).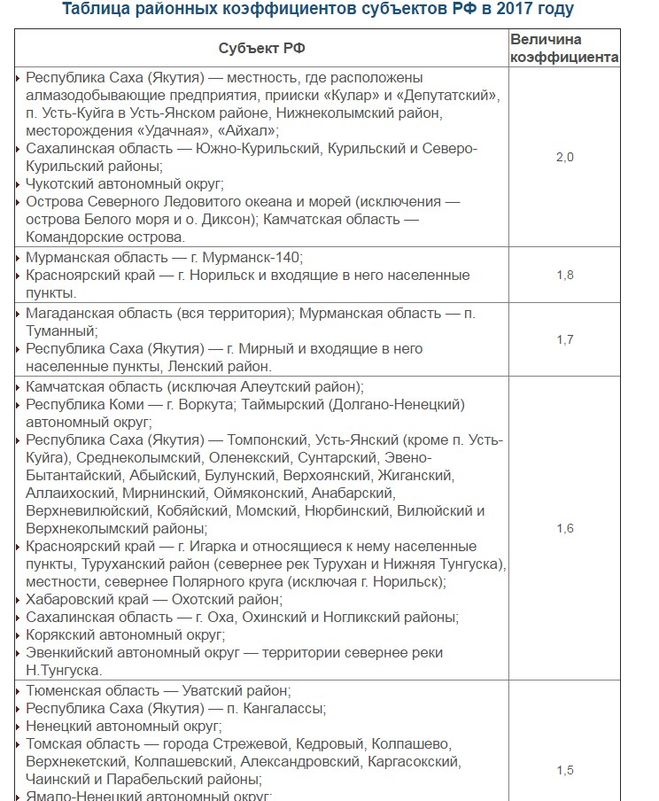
Таблица 4.1 из учебника обобщает распределение результатов тестов и соотношение учеников и учителей. Есть несколько функций, которые можно использовать для получения аналогичных результатов, например,
mean() (вычисляет среднее арифметическое предоставленных чисел),
sd() (вычисляет стандартное отклонение выборки),
quantile() (возвращает вектор указанных выборочных квантилей для данных).
Следующий фрагмент кода показывает, как этого добиться. Во-первых, мы вычисляем сводную статистику по столбцам STR и баллу CASchools. Чтобы получить хороший результат, мы собираем показатели в data.frame с именем DistributionSummary.
# вычислить выборочные средние значения STR и оценки avg_STR <- среднее (CASchools$STR) avg_score <- среднее (CASchools$score) # вычислить выборочные стандартные отклонения STR и оценки sd_STR <- sd(CASchools$STR) sd_score <- sd(CASchools$score) # установить вектор процентилей и вычислить квантили квантили <- c(0,10, 0,25, 0,4, 0,5, 0,6, 0,75, 0,9) quant_STR <- квантиль (CASchools$STR, квантили) quant_score <- квантиль (оценка CASchools $, квантили) # собрать все в data.frame DistributionSummary <- data.frame(Average = c(avg_STR, avg_score), Стандартное отклонение = c(sd_STR, sd_score), квантиль = rbind(quant_STR, quant_score)) # вывести сводку в консоль DistributionСводка #> Квантиль среднего стандартного отклонения.10. квантиль.25. квантиль.40. квантиль.50. квантиль.60. квантиль.75. #> quant_STR 19.64043 1,891812 17,3486 18,58236 19,26618 19,72321 20,0783 20,87181 #> quant_score 654.15655 19.053347 630.3950 640.05000 649.06999 654.45000 659.4000 666.66249 #> квантиль.90. #> quant_STR 21.86741 #> quant_score 678.85999
Что касается выборочных данных, мы используем plot(). Это позволяет нам обнаруживать характеристики наших данных, такие как выбросы, которые сложнее обнаружить, глядя на простые числа. На этот раз мы добавляем несколько дополнительных аргументов к вызову plot().
Первый аргумент в нашем вызове plot(), score ~ STR, снова является формулой, которая устанавливает переменные на осях y и x. Однако на этот раз две переменные не сохраняются в отдельных векторах, а представляют собой столбцы CASchools. Следовательно, R не найдет их, если данные аргумента не будут правильно указаны. данные должны соответствовать имени data.frame, которому принадлежат переменные, в данном случае CASchools. Дополнительные аргументы используются для изменения внешнего вида графика: в то время как main добавляет заголовок, xlab и ylab добавляют пользовательские метки к обеим осям.
Однако на этот раз две переменные не сохраняются в отдельных векторах, а представляют собой столбцы CASchools. Следовательно, R не найдет их, если данные аргумента не будут правильно указаны. данные должны соответствовать имени data.frame, которому принадлежат переменные, в данном случае CASchools. Дополнительные аргументы используются для изменения внешнего вида графика: в то время как main добавляет заголовок, xlab и ylab добавляют пользовательские метки к обеим осям.
сюжет(оценка ~ STR,
данные = CASchools,
main = "График рассеяния TestScore и STR",
xlab = "СИЛ (Х)",
ylab = «Оценка теста (Y)») График (рис. 4.2 в книге) показывает диаграмму рассеяния всех наблюдений по соотношению учеников и учителей и результатам теста. Мы видим, что точки сильно разбросаны, а переменные имеют отрицательную корреляцию. То есть мы ожидаем увидеть более низкие результаты тестов в больших классах.
Функцию cor() (дополнительную информацию см. в ?cor) можно использовать для вычисления корреляции между двумя числовых векторов.
cor(CASchools$STR, CASchools$score) #> [1] -0,2263627
Как видно из диаграммы рассеяния, корреляция отрицательна, но довольно слаба.
Теперь перед нами стоит задача найти линию, которая наилучшим образом соответствует данным. Конечно, мы могли бы просто ограничиться графическим просмотром и корреляционным анализом, а затем выбрать наиболее подходящую линию на глаз. Однако это было бы довольно субъективно: разные наблюдатели рисовали бы разные линии регрессии. В связи с этим нас интересуют методы, которые менее произвольны. Такой метод дается обычной оценкой методом наименьших квадратов (OLS). 92. \]
МНК-оценка в простой регрессионной модели представляет собой пару оценок для точки пересечения и наклона, которая минимизирует приведенное выше выражение. Вывод оценок МНК для обоих параметров представлен в Приложении 4.1 книги. Результаты обобщены в ключевой концепции 4.2.
Ключевая концепция 4.2
Оценщик МНК, предсказанные значения и остатки
МНК-оценки наклона \(\beta_1\) и точки пересечения \(\beta_0\) в простой модели линейной регрессии
\[\начать{выравнивать}
\hat\beta_1 & = \frac{ \sum_{i = 1}^n (X_i - \overline{X})(Y_i - \overline{Y}) } { \sum_{i=1}^n (X_i - \overline{X})^2}, \\
\\
\hat\beta_0 & = \overline{Y} - \hat\beta_1 \overline{X}. \конец{выравнивание}\]
Прогнозируемые значения OLS \(\widehat{Y}_i\) и остатки \(\hat{u}_i\) равны
\[\начать{выравнивать}
\widehat{Y}_i & = \hat\beta_0 + \hat\beta_1 X_i,\\
\\
\hat{u}_i & = Y_i - \widehat{Y}_i.
\конец{выравнивание}\]
\конец{выравнивание}\]
Прогнозируемые значения OLS \(\widehat{Y}_i\) и остатки \(\hat{u}_i\) равны
\[\начать{выравнивать}
\widehat{Y}_i & = \hat\beta_0 + \hat\beta_1 X_i,\\
\\
\hat{u}_i & = Y_i - \widehat{Y}_i.
\конец{выравнивание}\]
Оценивается точка пересечения \(\hat{\beta}_0\), параметр наклона \(\hat{\beta}_1\) и невязки \(\left(\hat{u}_i\right)\) из выборки \(n\) наблюдений \(X_i\) и \(Y_i\), \(i\), \(...\), \(n\). Это оценок точек пересечения неизвестной совокупности \(\left(\beta_0 \right)\), наклона \(\left(\beta_1\right)\) и члена ошибки \((u_i)\).
Формулы, представленные выше, на первый взгляд могут показаться не очень интуитивными. Следующее интерактивное приложение призвано помочь вам понять механизм OLS. Вы можете добавить наблюдения, щелкнув систему координат, в которой данные представлены точками. Когда доступны два или более наблюдений, приложение вычисляет линию регрессии, используя МНК и некоторые статистические данные, которые отображаются на правой панели. Результаты обновляются по мере добавления дополнительных наблюдений на левую панель. Двойной щелчок сбрасывает приложение, т. е. все данные удаляются. 92)
# вычислить beta_0_hat
beta_0 <- среднее (оценка) - beta_1 * среднее (STR)
# вывод результатов в консоль
бета_1
#> [1] -2,279808
бета_0
#> [1] 698.9329
Результаты обновляются по мере добавления дополнительных наблюдений на левую панель. Двойной щелчок сбрасывает приложение, т. е. все данные удаляются. 92)
# вычислить beta_0_hat
beta_0 <- среднее (оценка) - beta_1 * среднее (STR)
# вывод результатов в консоль
бета_1
#> [1] -2,279808
бета_0
#> [1] 698.9329
Вызов attach(CASchools) позволяет нам адресовать переменную, содержащуюся в CASchools, по ее имени: больше нет необходимости использовать оператор $ в сочетании с набором данных: R может напрямую оценивать имя переменной.
Rиспользует объект в пользовательской среде, если этот объект разделяет имя переменной, содержащейся в присоединенной базе данных. Однако лучше всегда использовать отличительные имена, чтобы избежать такой (кажущейся) амбивалентности!
Обратите внимание, что в остальной части этой главы мы обращаемся непосредственно к переменным, содержащимся в прикрепленном наборе данных CASchools!
Конечно, есть еще больше ручных способов выполнения этих задач. Поскольку OLS является одним из наиболее широко используемых методов оценки, R, конечно же, уже содержит встроенную функцию с именем lm() ( l inear m odel), которую можно использовать для проведения регрессионного анализа.
Поскольку OLS является одним из наиболее широко используемых методов оценки, R, конечно же, уже содержит встроенную функцию с именем lm() ( l inear m odel), которую можно использовать для проведения регрессионного анализа.
Первым аргументом функции, которую необходимо указать, является, подобно plot(), формула регрессии с основным синтаксисом y ~ x, где y — зависимая переменная, а x — независимая переменная. Данные аргумента определяют набор данных, который будет использоваться в регрессии. Теперь вернемся к примеру из книги, в котором анализируется взаимосвязь между результатами тестов и размерами классов. Следующий код использует lm() для воспроизведения результатов, представленных на рис. 4.3 книги.
# оценить модель и присвоить результат linear_model linear_model <- lm (оценка ~ STR, данные = CASchools) # вывести в консоль стандартный вывод оценочного объекта lm linear_model #> #> Вызов: #> lm(формула = оценка ~ STR, данные = CASchools) #> #> Коэффициенты: #> (Перехват) STR #> 698,93 -2,28
Добавим на график расчетную линию регрессии. На этот раз мы также увеличиваем диапазоны обеих осей, устанавливая аргументы xlim и ylim.
На этот раз мы также увеличиваем диапазоны обеих осей, устанавливая аргументы xlim и ylim.
# построить данные
сюжет(оценка ~ STR,
данные = CASchools,
main = "График рассеяния TestScore и STR",
xlab = "СИЛ (Х)",
ylab = "Оценка теста (Y)",
хлим = с(10, 30),
улим = с(600, 720))
# добавляем линию регрессии
abline(linear_model) Вы заметили, что на этот раз мы не передали параметры пересечения и наклона в abline? Если вы вызываете abline() для объекта класса lm, который содержит только один регрессор, R автоматически рисует линию регрессии!
Ссылки
Кляйбер, Кристиан и Ахим Цайлейс. 2020. AER: Прикладная эконометрика с R (версия 1.2-9). https://CRAN.R-project.org/package=AER.
Блок гидрографа Снайдера, модель
Страница загрузки Модель гидрографа блока Снайдера.
Основные понятия и уравнения
В 1938 году Снайдер опубликовал описание параметрического UH, разработанного им для анализа неисследованных водосборных бассейнов Аппалачского нагорья в США. Что еще более важно, он представил отношения для оценки параметров UH по характеристикам водораздела. Программа включает в себя реализацию Snyder UH.
Что еще более важно, он представил отношения для оценки параметров UH по характеристикам водораздела. Программа включает в себя реализацию Snyder UH.
Для своей работы Снайдер выбрал задержку, пиковый поток и общую временную базу в качестве критических характеристик UH. Он определил стандартный UH как такой, у которого продолжительность осадков tr связана с запаздыванием бассейна tp соотношением:
| t_{p}=5,5 t_{r} |
(Здесь запаздывание — это разница во времени пика UH и времени, связанного с центроидом гиетографа избыточных осадков, как показано на рисунке 25.) Таким образом, если продолжительность указана, запаздывание (и, следовательно, можно найти время пика UH) стандартного UH Снайдера. Если продолжительность желаемого UH для интересующего водосбора значительно отличается от времени, заданного уравнением 30, для определения взаимосвязи пикового времени UH и продолжительности UH можно использовать следующее соотношение:
| t_{p R}=t_{p}-\frac{t_{r}-t_{R}}{4} |
, где tR = продолжительность желаемого UH; и tpR = отставание желаемого UH.
Для стандартного случая Снайдер обнаружил, что запаздывание UH и пик на единицу избыточных осадков на единицу площади водосбора связаны соотношением:
| \frac{U_{p}}{A}=C \frac{C_{p}}{t_{p}} |
где Up = пик стандартного UH; A = площадь водосбора водораздела; Cp = коэффициент пиков UH; и C = константа преобразования (2,75 для системы СИ или 640 для системы футо-фунтов).
Рис. 30. Гидрограф Снайдера.
Для другой длительности пик UH, QpR, определяется как:
| \frac{U_{p R}}{A}=C \frac{C_{p}}{t_{p R}} |
UH-модель Снайдера требует указания стандартной задержки tp и коэффициента Cp. Программа устанавливает tpR в уравнении 31 равным указанному временному интервалу и решает уравнение 31, чтобы найти отставание требуемого UH. Наконец, уравнение 33 решается для нахождения пика UH. Снайдер предложил соотношение, с помощью которого можно определить общую временную базу UH. Вместо этого отношения программа использует вычисленный пик UH и время пика, чтобы найти эквивалент UH с моделью Кларка (см. следующий раздел). Исходя из этого, он определяет базу времени и все ординаты, кроме пика UH. 9{0.3}
Программа устанавливает tpR в уравнении 31 равным указанному временному интервалу и решает уравнение 31, чтобы найти отставание требуемого UH. Наконец, уравнение 33 решается для нахождения пика UH. Снайдер предложил соотношение, с помощью которого можно определить общую временную базу UH. Вместо этого отношения программа использует вычисленный пик UH и время пика, чтобы найти эквивалент UH с моделью Кларка (см. следующий раздел). Исходя из этого, он определяет базу времени и все ординаты, кроме пика UH. 9{0.3}
где Ct = бассейновый коэффициент; L = длина основного потока от выхода до водораздела; Lc = длина вдоль основного русла от устья до точки, ближайшей к центроиду водораздела; и C = константа преобразования (0,75 для системы СИ и 1,00 для системы фут-фунт).
Параметр Ct уравнения 34 и Cp уравнения 32 лучше всего найти с помощью калибровки, поскольку они не являются физическими параметрами. Бедиент и Хубер (1992) сообщают, что Ct обычно колеблется от 1,8 до 2,2, хотя было обнаружено, что он колеблется от 0,4 в горных районах до 8,0 вдоль Мексиканского залива.
 000002 636,3 650,9
#> 4 0,000000 651,9 643,5
#> 5 13,857677 641,8 639,9
#> 6 12.408759 605.7 605.4
000002 636,3 650,9
#> 4 0,000000 651,9 643,5
#> 5 13,857677 641,8 639,9
#> 6 12.408759 605.7 605.4  frame
DistributionSummary <- data.frame(Average = c(avg_STR, avg_score),
Стандартное отклонение = c(sd_STR, sd_score),
квантиль = rbind(quant_STR, quant_score))
# вывести сводку в консоль
DistributionСводка
#> Квантиль среднего стандартного отклонения.10. квантиль.25. квантиль.40. квантиль.50. квантиль.60. квантиль.75.
#> quant_STR 19.64043 1,891812 17,3486 18,58236 19,26618 19,72321 20,0783 20,87181
#> quant_score 654.15655 19.053347 630.3950 640.05000 649.06999 654.45000 659.4000 666.66249
#> квантиль.90.
#> quant_STR 21.86741
#> quant_score 678.85999
frame
DistributionSummary <- data.frame(Average = c(avg_STR, avg_score),
Стандартное отклонение = c(sd_STR, sd_score),
квантиль = rbind(quant_STR, quant_score))
# вывести сводку в консоль
DistributionСводка
#> Квантиль среднего стандартного отклонения.10. квантиль.25. квантиль.40. квантиль.50. квантиль.60. квантиль.75.
#> quant_STR 19.64043 1,891812 17,3486 18,58236 19,26618 19,72321 20,0783 20,87181
#> quant_score 654.15655 19.053347 630.3950 640.05000 649.06999 654.45000 659.4000 666.66249
#> квантиль.90.
#> quant_STR 21.86741
#> quant_score 678.85999
Об авторе