Как заполнить форму 0503169: Форма 0503169 для казенных учреждений: как заполнить и сдать?

Содержание

Форма 0503169 для казенных учреждений: как заполнить и сдать?

Смотрите новую статью «Форма 0503169 в 2018 году: заполняем правильно»

Форма отчетности 0503169 (Сведения по дебиторской и кредиторской задолженности) – одна из составляющих анализа показателей бухгалтерской отчетности для казенных учреждений. Стабильный учет помогает грамотно отслеживать расход бюджетных средств и плодотворность расхода.

Форму 0503169 составляют те, кто отвечает за бюджетные средства: например, получатели бюджетных средств, администратор доходов бюджета и администратор источников финансирования дефицита бюджета.

Из чего состоит форма 0503169?

Согласно п. 167 Приказа Минфина РФ от 28.12.2010 г. № 191н в форму 0503169 следует вносить общую информацию о кредиторской и дебиторской задолженности (в том числе и о просроченной).

Для составления отчетности по задолженности, в форме отражаются счета бухгалтерского учета.

Для кредиторской задолженности это счета:

0. 205.00.000 «Расчеты по доходам»;
0.208.00.000 «Расчеты с подотчетными лицами»;
0.209.00.000 «Расчеты по ущербу и иным доходам»;
0.302.00.000 «Расчеты по принятым обязательствам»;
0.303.00.000 «Расчеты по платежам в бюджеты»;
0.304.00.000 «Прочие расчеты с кредиторами».

Для дебиторской задолженности:

0.205.00.000 «Расчеты по доходам»;
0.206.00.000 «Расчеты по выданным авансам»;
0.208.00.000 «Расчеты с подотчетными лицами»;
0.209.00.000 «Расчеты по ущербу и иным доходам»;
0.303.00.000 «Расчеты по платежам в бюджеты».

Сама форма отчетности имеет два раздела: в первом указывается важная информация по кредиторской и дебиторской задолженности, второй рассматривает только просроченные задолженности.

Как правильно заполнить и сдать форму 0503169?

Форму отчетности нужно заполнить отдельно по кредиторской и дебиторской задолженности, а также раздельно по видам деятельности (бюджетная, средства во временном распоряжении). Все отображенные показатели следует подкрепить фактами из регистров бюджетного учета, об этом говорится в пунктах 7 и 167 Инструкции, утвержденной Приказом Минфина РФ от 28.12.2010 г. № 191н.

Первый раздел формы 0503169 имеет 14 граф (Приложение Приказа Минфина РФ от 28.12.2010 г. № 191н).

В графах 2, 9 и 12 указывается общая сумма задолженности на начало года, конец отчетного периода и на конец аналогичного периода прошлого финансового года.
В графах 3,10 и 13 отражается сумма долгосрочной задолженности на начало года, конец отчетного периода и конец прошлогоднего отчетного периода.

В графах 4,11 и 14 указывается сумма просроченной задолженности на начало года, конец отчетного периода текущего года и аналогичного прошлого.
В графах 5 и 6 указывается увеличение суммы задолженности, в т.ч. неденежные расчеты.
В графах 7 и 8 отражается уменьшение суммы задолженности, в т.ч. неденежные расчеты.

Второй раздел приложения менее объемный, заполнять необходимо всего восемь граф.

В графе 1 указываются номера счетов бюджетного учета, по которым вы отразили остатки в 11-й графе первого раздела формы.
Во 2 графе отражается сумма долга.
В 3 и 4 графах указываются дата появления долга и дата его обязательного погашения по договору.
В графах 5 и 6 указываются ИНН кредитора или дебитора и его наименование;

В графах 7 и 8 указываются код причины образования просрочки и пояснения.

Форма отчетности 0503169 сдается ежеквартально и раз в год. Ежеквартальная отчетность составляется на 1 апреля, 1 июля и 1 октября; годовая – 1 января года, следующего за отчетным.

Опубликовано 31.01.2017

Форма 0503169/0503769: особенности заполнения за первое полугодие в 1С: БГУ 8

Смотрите также статью:

«Особенности составления форм 0503169 и 0503769»

Близится отчетность за первое полугодие 2021 года. В перечень форм, представляемых на 1 июля текущего года, входят Сведения по дебиторской и кредиторской задолженности (ф.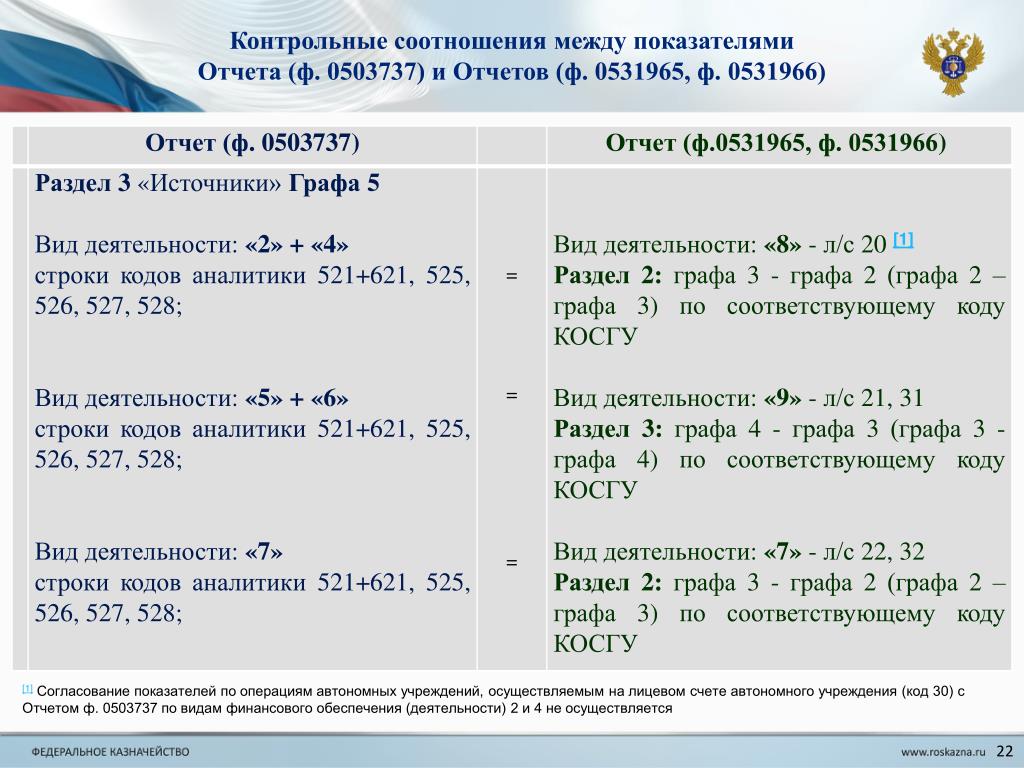 0503169, ф. 0503769). В статье рассмотрим, что учесть при заполнении Сведений (ф. 0503169, ф. 0503769) за первое полугодие 2021 года.

Сведения (ф. 0503169, ф. 0503769) заполняются в соответствии с п. 167 Инструкции, утв. приказом Минфина России от 28.12.2010 № 191н, п. 69 Инструкции, утв. приказом Минфина России от 25.03.2011 № 33н.

Последние изменения в порядок заполнения Сведений (ф. 0503169, ф. 0503769) внесены приказами Минфина России от 16.12.2020 № 311н, от 30.11.2020 № 292н. При этом некоторые нормы, вводимые этими приказами, применяются, начиная с отчетности за первое полугодие 2021 года.

Так, начиная с отчетности на 1 июля 2021 г., в графе 1 Сведений (ф. 0503169, ф. 0503769) по счетам 205, 206, 208, 209, 210 10, 210 05 в 24 — 25 разрядах номера счета ставятся нули, а в 26 разряде номера счета — третий разряд соответствующей подстатьи КОСГУ «Увеличения прочей дебиторской задолженности».

Например, подстатья 564 будет иметь вид 004 (например, 0 206 ХХ 004, 0 209 ХХ 004).

Аналогичный подход применяется по счетам 302, 303, 304 02, 304 03, 304 06, в 24-26 разрядах номера счета которых указываются коды 730 (830) КОСГУ.

Например, подстатья 731 будет иметь вид 001 (например, 0 303 07 001).

В Сведения (ф. 0503169, ф. 0503769) включаются данные по долгосрочной и просроченной задолженности. Эти сведения отражаются в графах 3, 10, 13 раздела «1. Сведения о дебиторской (кредиторской) задолженности», а данные по просроченной задолженности – в графах 4, 11, 14 раздела «1. Сведения о дебиторской (кредиторской) задолженности».

Обратите внимание, что 13.05.2021 Минфином России подготовлены проекты о внесении изменений в Инструкции по составлению отчетности №№ 191, 33н. Согласно проектам графы 3, 10, 13 Сведений (ф. 0503169, ф. 0503769) планируется заполнять только в годовой отчетности на 1 января года, следующего за отчетным. Следовательно, в составе полугодовой отчетности эти графы планируется оставить пустыми. Однако, проекты — это не нормативные акты и представлены для ознакомления, поэтому, на текущий момент, эти графы заполняются «по-старому».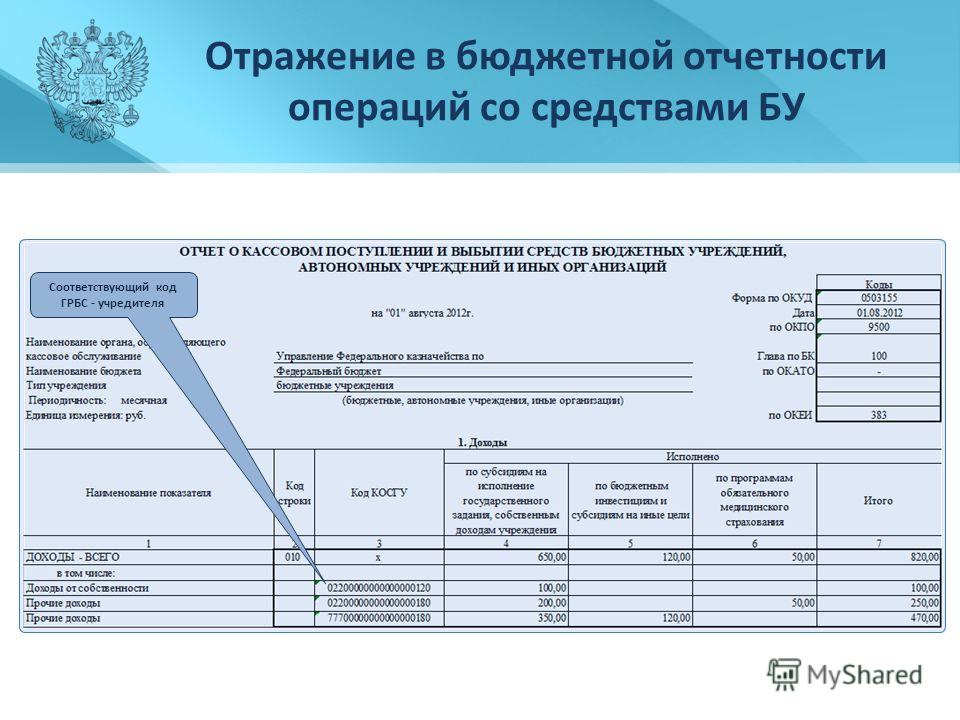

Коды для объяснения причин образования просроченной задолженности в разделе 2 Сведений (ф. 0503169), введенные Приказом № 311н, по-прежнему действуют. Эти коды уже применялись в отчетности за 2020 г.

Аналогичные коды предусмотрены для Сведений (ф. 0503769) в проекте приказа Минфина России о внесении изменений в Инструкцию № 33н.

Для формирования остатков по кодам Классификации институциональных единиц (001 – 009), указываемым в 26 разряде счетов расчетов, вводится документ Формирование остатков

по счетам расчетов (раздел Учет и отчетность — Помощник закрытия периода). Дата документа — 31 декабря.

Из документа можно сформировать Бухгалтерскую справку (ф. 0504833) (кнопка Печать – Справка ф. 0504833).

Данные по долгосрочной и просроченной задолженности отражаются на основании данных инвентаризации расчетов с контрагентами (раздел Учет и отчетность — Документы инвентаризации).

Соответствующие показатели найдут свое отражение в Сведениях (ф. 0503169, ф. 0503769). Отчет заполнится автоматически по кнопке Заполнить.

Опубликовано 16.06.2021

Потенциал потока типа IIA, 4-формы и аномалии Фрида-Виттена

Р. Буссо и Дж. Полчински, Квантование потоков четырех форм и динамическая нейтрализация космологической постоянной

, JHEP 06 (200009) 006 [hep-th/0004134] [ВДОХНОВЕНИЕ].

Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый

Дж. Д. Браун и К. Тейтельбойм, Нейтрализация космологической постоянной путем создания мембран , Нукл. физ. B 297 (1988) 787 [ВДОХНОВЕНИЕ].

Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый

Дж. Д. Браун и К. Тейтельбойм, Динамическая нейтрализация космологической постоянной , Phys. лат. B 195 (1987) 177 [ВДОХНОВЕНИЕ].

Артикул ОБЪЯВЛЕНИЯ Google ученый

М. Дж. Дафф и П. ван Ньювенхуизен, Квантовая неэквивалентность различных представлений полей

, Phys. лат. 94B (1980) 179 [ВДОХНОВЕНИЕ].

Артикул ОБЪЯВЛЕНИЯ Google ученый

С.В. Хокинг, Космологическая постоянная, вероятно, равна нулю , Phys. лат. 134B (1984) 403 [ВДОХНОВЕНИЕ].

Артикул ОБЪЯВЛЕНИЯ Google ученый

М. Дж. Дафф, Космологическая постоянная, возможно, равна нулю, но доказательство, вероятно, неверно , Phys. лат. B 226 (1989) 36 [ВДОХНОВЕНИЕ].

Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый

З.К. Wu, Космологическая постоянная, вероятно, равна нулю, и доказательство, возможно, верное

, Phys. лат. B 659 (2008) 891 [arXiv:0709.3314] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый

М.Дж. Дункан и Л.Г. Jensen, Четыре формы и обращение в нуль космологической постоянной , Nucl. физ. B 336 (1990) 100 [ВДОХНОВЕНИЕ].

Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый

Дж. Л. Фэн, Дж. Марч-Рассел, С. Сетхи и Ф. Вилчек, Сальтаторная релаксация космологической постоянной , Nucl. физ. B 602 (2001) 307 [hep-th/0005276] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый

Г. Двали,

Большие иерархии из аттракторного вакуума , Phys. Ред. D 74 (2006) 025018 [hep-th/0410286] [INSPIRE].

ОБЪЯВЛЕНИЕ MathSciNet Google ученый

Двали Г., Трехмерное измерение симметрии аксионов и гравитации , hep-th/0507215 [INSPIRE].

Г. Двали, Вакуумное накопление решения сильной задачи CP , Phys. Ред. D 74 (2006) 025019 [hep-th/0510053] [INSPIRE].

ОБЪЯВЛЕНИЕ MathSciNet Google ученый

Г. Двали, С. Фолкертс и А. Франка, Как нейтрино защищает аксион , Физ. Ред. D 89 (2014) 105025 [arXiv:1312.7273] [INSPIRE].

ОБЪЯВЛЕНИЕ Google ученый

Н. Калопер и Л. Сорбо, Естественная основа для хаотической инфляции , Phys. Преподобный Летт. 102 (2009) 121301 [arXiv:0811.1989] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ Google ученый

К. Грох, Дж. Луи и Дж. Зоммерфельд, Двойственность и сопряжения 3-форм-мультиплетов в N = 1 суперсимметрия , JHEP 05 (6421arXiv 0:4212arXiv)] [ВДОХНОВЛЯТЬ].

Артикул ОБЪЯВЛЕНИЯ Google ученый

Н. Калопер, А. Лоуренс и Л. Сорбо, Неблагородный подход к раздуванию больших полей , JCAP 03 (2011) 023 [arXiv:1101.0026] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ Google ученый

Ф. Марчесано, Г. Шиу и А.М. Уранга, F-термин Аксион Монодромия Инфляция , JHEP 09 (2014) 184 [arXiv:1404.3040] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ Google ученый

Э. Дудас, Мультиплет трех форм и инфляция , JHEP 12 (2014) 014 [arXiv:1407.5688] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ Google ученый

С. Бильман, Л.Э. Ибаньес и И. Валенсуэла, 3-формы Минковского, вакуум струны потока, устойчивость аксионов и естественность , JHEP 12 (2015) 119 [arXiv:1507.06793] [INSPIRE].

ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Google ученый

E. García-Valdecasas and A. Uranga, О 3-формальной формулировке аксионных потенциалов от D-бранных инстантонов , JHEP 02 (2017) 087 [arXiv: 16925.] .

F. Carta, F. Marchesano, W. Staessens and G. Zoccarato, Многоветвящиеся открытые струны и потенциалы Кэлера , JHEP 09 (2016) 062 [arXiv:1606.00508] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ МАТЕМАТИКА Google ученый

И. Валенсуэла, Вопросы обратной реакции в аксионной монодромии и 4-формах Минковского , JHEP 06 (2017) 098 [arXiv:1611.00394] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый

И. Валенсуэла, Обратная реакция в аксионной монодромии, 4-формы и болото , PoS(CORFU2016)112 [arXiv:1708.07456] [INSPIRE].

Ф. Фаракос, С. Ланца, Л. Мартуччи и Д. Сорокин, Три формы в супергравитации и компактификации потоков , Eur. физ. J. C 77 (2017) 602 [arXiv:1706.09422] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ Google ученый

Ф. Фаракос, С. Ланца, Л. Мартуччи и Д. Сорокин, Три формы, суперсимметрия и компактификации струн , arXiv:1712.09366 [INSPIRE].

С. Качру, Р. Каллош, А. Д. Линде и С.П. Триведи, Вакуум де Ситтера в теории струн , Phys. Ред. D 68 (2003) 046005 [hep-th/0301240] [INSPIRE].

В. Баласубраманян, П. Берглунд, Дж. П. Конлон и Ф. Кеведо, Систематика стабилизации модулей в компактификациях потоков Калаби-Яу , JHEP 03 (2005) 007 [hep-th/0502058] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый

J.P. Conlon, F. Quevedo и K. Suruliz, Compactifications Flux с большим объемом: DAMULI Spectrum и D 3 /D 7 Soft SuperSymmetry. hep-th/0505076] [ВДОХНОВЕНИЕ].

Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый

M.R. Douglas and S. Kachru, Компактификация флюса , Rev. Mod. физ. 79 (2007) 733 [hep-th/0610102] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый

Ф.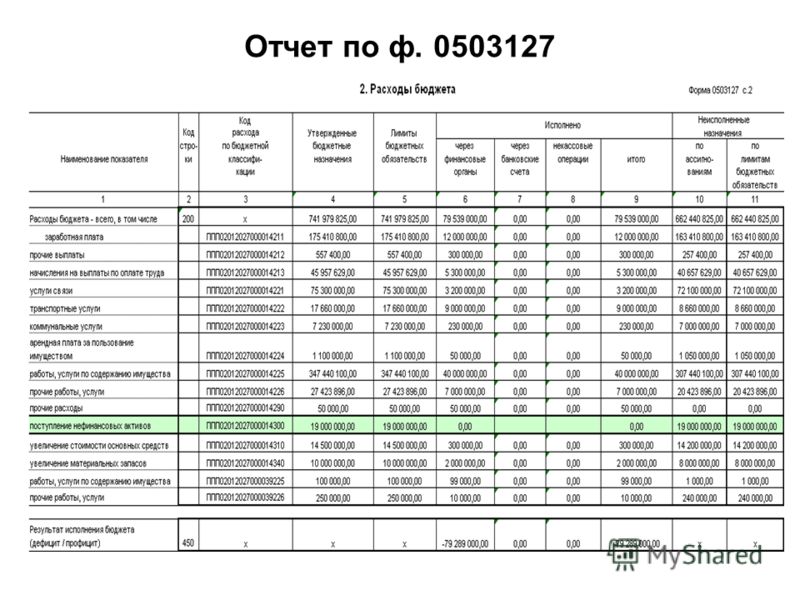 Кеведо, Локальные струнные модели и модули стабилизации , Мод. физ. лат. A 30 (2015) 1530004 [arXiv:1404.5151] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый

O. DeWolfe, A. Giryavets, S. Kachru and W. Taylor, Стабилизация модулей типа IIA , JHEP 07 (2005) 066 [hep-th/0505160] [INSPIRE].

ОБЪЯВЛЕНИЕ MathSciNet Google ученый

П.Г. Камара, А. Фонт и Л.Е. Ibáñez, Потоки, фиксация модулей и MSSM-подобный вакуум в простой ориентифолде IIA , JHEP 09 (2005) 013 [hep-th/0506066] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый

G. Villadoro и F. Zwirner, N = 1 Эффективный потенциал из двойного типа IIA D 6 /O 6 Ориентации с общими потоками , JHEP 06 (2005) 047, JHEP 06 (2005) 047, JHEP 06 (2005) 047, JHEP 06 (2005) 047, JHEP 06 (2005) 047, JHEP 06 (2005) 047, JHEP 06 (2005) 047, JHEP 06 (2005). [hep-th/0503169] [ВДОХНОВЕНИЕ].

Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый

Г. Алдасабал, П.Г. Камара, А. Фонт и Л.Е. Ibáñez, Больше двойных потоков и модулей крепления , JHEP 05 (2006) 070 [hep-th/0602089] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый

J. Shelton, W. Taylor and B. Wecht, Негеометрические компактификации потоков , JHEP 10 (2005) 085 [hep-th/0508133] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый

Б. де Карлос, А. Гуарино и Дж. М. Морено, Полная классификация пустот Минковского в обобщенных моделях потоков , JHEP 02 (2010) 076 [arXiv:0911.2876] [INSPIRE].

Артикул MathSciNet МАТЕМАТИКА Google ученый

Б. де Карлос, А. Гуарино и Дж. М. Морено, Стабилизация модулей потока, алгебры супергравитации и запретные теоремы , JHEP 01 (2010) 012 [arXiv:0907.5580] [ВДОХНОВЕНИЕ].

Артикул MathSciNet МАТЕМАТИКА Google ученый

U. Danielsson and G. Dibitetto, О распределении стабильных вакуумов де Ситтера , JHEP 03 (2013) 018 [arXiv:1212.4984] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ Google ученый

Т.В. Гримм и Д. Виейра Лопес, 9 лет0004 N = 1 эффективных действий D-бран в ориентифолдах типа IIA и IIB , Nucl. физ. B 855 (2012) 639 [arXiv:1104.2328] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый

M. Kerstan и T. Weigand, Эффективное действие D 6 -Branes в N = 1 Type IIA Oniversits , JHEP 06 (2011) 105 [Arxiv: 1104. 232299 06 (2011) 105 [Arxiv: 1104.232299 06 (2011).] [ВДОХНОВЛЯТЬ].

Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый

Д. С. Фрид и Э. Виттен, Аномалии в теории струн с D-бранами , Asian J. Math. 3 (1999) 819 [hep-th/9

9] [INSPIRE].

Артикул MathSciNet МАТЕМАТИКА Google ученый

Дж. М. Малдасена, Г.В. Мур и Н. Зайберг, инстантона D-браны и заряды k-теории , JHEP 11 (2001) 062 [hep-th/0108100] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый

М. Берасалус-Гонсалес, П.Г. Камара, Ф. Марчесано и А.М. Uranga, Заряженные браны Zp в компактификациях потока , JHEP 04 (2013) 138 [arXiv:1211. 5317] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ МАТЕМАТИКА Google ученый

Э. Сильверстайн и А. Вестфаль, Монодромия в реликтовом излучении: гравитационные волны и инфляция струн , Phys. Ред. D 78 (2008) 106003 [arXiv:0803.3085] [INSPIRE].

ОБЪЯВЛЕНИЕ Google ученый

Л. Макаллистер, Э. Сильверстайн и А. Вестфаль, Гравитационные волны и линейная инфляция из аксионной монодромии , Phys. Ред. D 82 (2010) 046003 [arXiv:0808.0706] [INSPIRE].

ОБЪЯВЛЕНИЕ Google ученый

Д. Бауманн и Л. Макаллистер, Инфляция и теория струн , Cambridge University Press, Кембридж, Великобритания (2015), arXiv:1404.2601] [INSPIRE].

A. Westphal, Струнная космология — Инфляция большого поля в теории струн , Междунар. Дж. Мод. физ. A 30 (2015) 1530024 [arXiv:1409.5350] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый

S. Bielleman et al., Инфляция Хиггса и стабилизация модулей , JHEP 02 (2017) 073 [arXiv:1611.07084] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый

Р. Блюменхаген, И. Валенсуэла и Ф. Вольф, Гипотеза болот и инфляция аксионной монодромии с F-членом , JHEP 07 (2017) 145 [arXiv:177RE.05PI].

Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый

Л.Э. Ибаньес и А.М. Уранга, Теория струн и физика элементарных частиц: введение в феноменологию струн , Cambridge University Press, Кембридж, Великобритания (2012).

МАТЕМАТИКА Google ученый

Р. Блюменхаген, М. Цветич, П. Лангакер и Г. Шиу, На пути к реалистичным моделям пересекающихся D-бран , Анн. Преподобный Нукл. Часть. науч. 55 (2005) 71 [hep-th/0502005] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ Google ученый

Р. Блюменхаген, Б. Кёрс, Д. Люст и С. Штибергер, Четырехмерные струнные компактификации с D-бранами, ориентифолдами и потоками , Phys. Представитель 445 (2007) 1 [hep-th/0610327] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый

F. Marchesano, Прогресс в построении модели D-браны , Fortsch. физ. 55 (2007) 491 [hep-th/0702094] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый

А.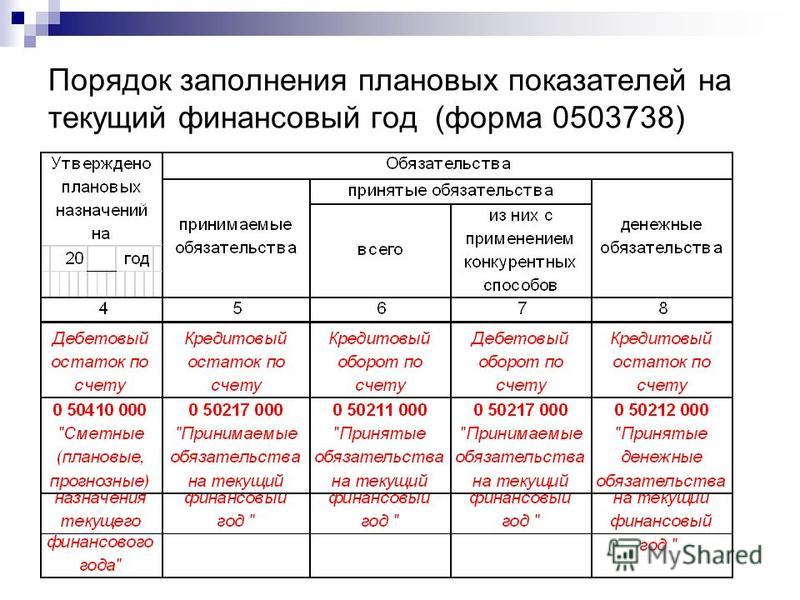 Фонт, Л.Э. Ibáñez and F. Marchesano, Coisotropic D 8 -branes and model-building , JHEP 09 (2006) 080 [hep-th/0607219] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый

Т.В. Grimm and J. Louis, Эффективное действие ориентифолдов типа IIA Калаби-Яу , Nucl. физ. B 718 (2005) 153 [hep-th/0412277] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый

J. Louis and A. Micu, Теории типа 2, компактифицированные на трехмерных многообразиях Калаби-Яу в присутствии фоновых потоков , Нукл. физ. B 635 (2002) 395 [hep-th/0202168] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый

С. Качру и А.-К. Kashani-Poor, Потенциалы модулей в компактификациях типа IIA с потоком RR и NS , JHEP 03 (2005) 066 [hep-th/0411279] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый

E. Bergshoeff et al., Новые формулировки суперсимметрии D = 10 и класса D 8 -O 8 доменных стенок , . Квант. Грав. 18 (2001) 3359 [hep-th/0103233] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый

Р.К. McLean, Деформации калиброванных подмногообразий , Общ. Анальный. геом. 6 (1998) 705.

Артикул MathSciNet МАТЕМАТИКА Google ученый

F. Marchesano, D. Regalado and G. Zoccarato, О стабилизации модулей D-браны , JHEP 11 (2014) 097 [arXiv:1410.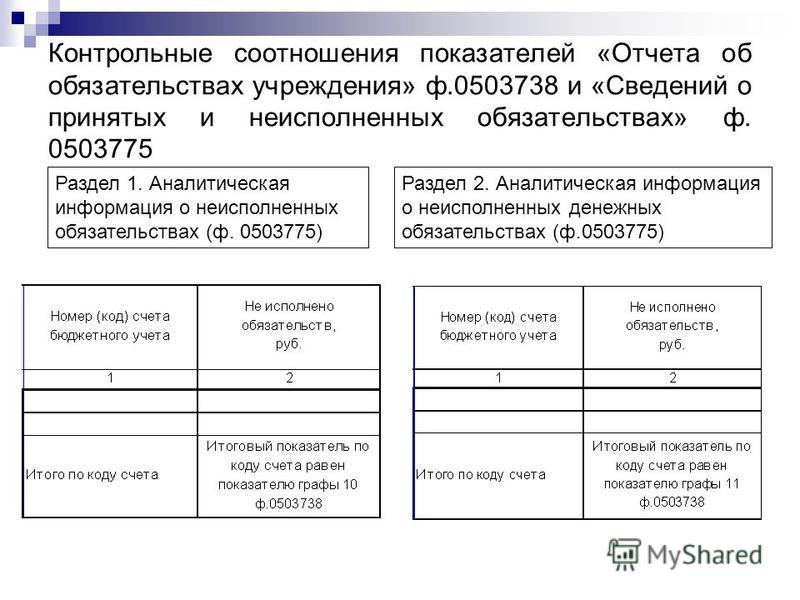 0209] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый

Д. Эскобар, А. Ландете, Ф. Марчесано и Д. Регаладо, Инфляция большого поля от D-бран , Phys. Ред. D 93 (2016) 081301 [arXiv:1505.07871] [INSPIRE].

ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Google ученый (2016) ].

Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый

Х. Триендл, личное сообщение.

Р. Блюменхаген, А. Фонт и Э. Плаушинн, Связь теории двойного поля со скалярным потенциалом N [ВДОХНОВЛЯТЬ].

ОБЪЯВЛЕНИЕ MathSciNet МАТЕМАТИКА Google ученый

X. Gao, P. Shukla and R. Sun, Симплектическая формулировка негеометрического скалярного потенциала типа IIA , Физ. Ред. D 98 (2018) 046009 [arXiv:1712.07310] [INSPIRE].

ОБЪЯВЛЕНИЕ Google ученый

Г. Алдасабал, неопубликованные заметки (2017 г.).

Г. Альдасабаль, Д. Маркес, К. Нуньес и Х.А. Rosabal, По модулям стабилизации типа IIB и N = 4 , 8 супергравитаций , Nucl. физ. B 849 (2011) 80 [arXiv:1101.5954] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый

А. Ханани и Э. Виттен, Суперструны типа IIB, монополи BPS и трехмерная калибровочная динамика , Nucl. физ. B 492 (1997) 152 [hep-th/9611230] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый

С. Гукова, К. Вафы и Э. Виттена, CFT ’ s из Калаби-Яу четыре складки , Nucl. физ. B 584 (2000) 69 [ Erratum ibid. B 608 (2001) 477] [hep-th/90] [INSPIRE].

Т.Р. Тейлор и К. Вафа, RR Поток R на Калаби-Яу и частичное нарушение суперсимметрии , Phys. лат. B 474 (2000) 130 [hep-th/9_{2] [INSPIRE].}

Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый

P. Candelas and X. de la Ossa, Пространство модулей многообразий Калаби-Яу , Nucl. физ. B 355 (1991) 455 [ВДОХНОВЕНИЕ].

Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый

Д. Марольф, Термины Черна-Саймонса и три понятия заряда , hep-th/0006117 [INSPIRE].

F. Marchesano, D 6 -браны и кручения , JHEP 05 (2006) 019 [hep-th/0603210] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый

М. Гранья, Р. Минасян, М. Петрини и А. Томаселло, Скан для новых N = 1 вакуумов на скрученных торах , JHEP 05 (23107) /0609124] [ВДОХНОВЕНИЕ].

Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый

E. Palti, G. Tasinato and J. Ward, WEAKLY-coupled IIA Flux Compactifications , JHEP 06 (2008) 084 [arXiv:0804.1248] [INSPIV:0804.1248].

Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый

Д. Люст, Ф. Марчезано, Л. Мартуччи и Д. Цимпис, Обобщенный несуперсимметричный поток вакуума , JHEP 11 (2008) 021 [arXiv:08007.45RE]INS].

Артикул MathSciNet Google ученый

P.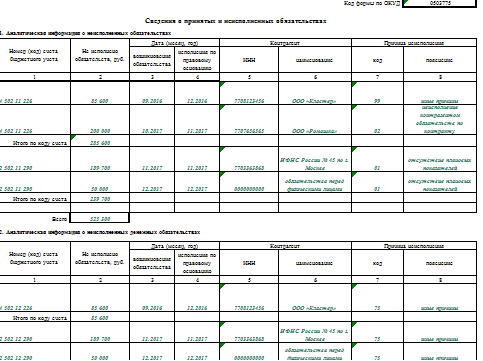 Koerber and D. Tsimpis, Суперсимметричные источники, интегрируемость и компактификации обобщенной структуры , JHEP 08 (2007) 082 [arXiv:0706.1244] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый

Х. Джокерс и Дж. Луи, Эффективное действие D 7 -браны в N = 1 Калаби-Яу ориентифолды , Nucl. физ. B 705 (2005) 167 [hep-th/0409098] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый

Н. Дж. Хитчин, Пространство модулей специальных лагранжевых подмногообразий , Annali Scuola Sup. Норма. Пизанская науч. Фис. Мат. 25 (1997) 503 [dg-ga/9711002] [INSPIRE].

П. Кербер и Л. Мартуччи, От десяти к четырем и обратно: как обобщить геометрию

Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый

P. Koerber, Лекции по обобщенной комплексной геометрии для физиков , Fortsch. физ. 59 (2011) 169 [arXiv:1006.1536] [ВДОХНОВЕНИЕ].

Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый

Ф. Марчесано, Д. Регаладо и Г. Зоккарато, U(1) 9Смешивание 0004 и линейная эквивалентность D-бран , JHEP 08 (2014) 157 [arXiv:1406.2729] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ МАТЕМАТИКА Google ученый

S. Gurrieri, J. Louis, A. Micu and D. Waldram, Зеркальная симметрия в обобщенных компактификациях Калаби-Яу , Nucl. физ. B 654 (2003) 61 [hep-th/0211102] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый

Р. П. Томас, Карты моментов, монодромия и зеркальные многообразия , в Симплектическая геометрия и зеркальная симметрия. Труды 4-й ежегодной международной конференции KIAS, Сеул, Южная Корея, 14–18 августа 2000 г. , стр. 467–498, 2001 г., math/0104196 [INSPIRE].

Л. Мартуччи, D-браны на общем фоне N = 1 : суперпотенциалы и D-термы , JHEP 06 (2006) 033 [hep-1RE/060INSPI].

Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый

M. Berasaluce-Gonzalez et al., Неабелевы дискретные калибровочные симметрии в 4 моделях d-струн , JHEP 09 (2012) 3.arxivRE 0518].

Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый

П.Г. Камара, К. Кондееску и Э. Дудас, Голоморфные переменные в моделях намагниченных бран с непрерывными линиями Вильсона , JHEP 04 (2010) 029 [arXiv:0912. 3369] [INSPIRE].

Артикул ОБЪЯВЛЕНИЯ MathSciNet МАТЕМАТИКА Google ученый

Энтропия | Бесплатный полнотекстовый | Простой декодер для топологических кодов

1. Введение

Коды с исправлением квантовых ошибок являются неотъемлемой частью предложений по квантовым вычислениям. Коды с исправлением топологических ошибок в настоящее время являются одним из наиболее хорошо изученных примеров [1]. Никакой код бесполезен без декодера, который берет классическую информацию, полученную в результате измерения кода, и использует ее, чтобы определить, как лучше противодействовать эффектам шума. Было предложено несколько алгоритмов для декодирования топологических кодов, каждый из которых имеет различные преимущества и недостатки.

Здесь мы представляем алгоритм, основным преимуществом которого является его простота, допускающая прямое обобщение на множество топологических кодов, а также на более экзотические задачи декодирования, такие как неабелевское декодирование [2]. Его можно рассматривать как пример декодера HDRG, который в последнее время стал привлекать внимание [3–5], и связан с алгоритмом «расширяющихся ромбов», изученным в [6].

Для сравнения метода с существующими мы применяем его к конкретному выбору кода и модели ошибки. Наиболее широко изучаемыми топологическими кодами являются поверхностные коды [7]. Именно поэтому мы используем их для нашего бенчмаркинга. Мы специально используем планарный код, чтобы продемонстрировать, как наш алгоритм работает с границами. К этому коду применялось множество методов декодирования [8–10], что делает его лучшим выбором для сравнения нашего алгоритма.

Первичная модель ошибки, которую мы рассматриваем, является стандартной моделью, применяемой к планарному коду. При этом ошибки действуют независимо на каждом вращении, а перевороты битов и фаз происходят независимо друг от друга. Однако, поскольку в реальных физических системах, скорее всего, будут возникать ошибки, коррелирующие между спинами [11–13], мы также рассматриваем модель ошибок с корреляциями ближайших соседей между ошибками.

Мы также используем недавнее исследование декодеров HDRG [5], примером которого является предлагаемый нами метод. В этой работе предлагается улучшенная метрика расстояния, которую можно использовать в таких декодерах для повышения производительности таких кодов, как планарный код. Изучаем производительность нашего декодера как с этой модификацией, так и без нее.

2. Плоский код

Плоский код является плоским вариантом поверхностных кодов, введенных Китаевым [7,14]. Он определен на спиновой решетке, как на рисунке 1, с частицей со спином 1/2 в каждой вершине. Существует два типа пластинок, обозначенных s и p, для которых мы определяем эрмитовы операторы следующим образом:

Эти операторы взаимно коммутируют и являются стабилизирующими операторами кода. Их собственные значения можно интерпретировать с точки зрения анионических занятий, при этом ни один ион не присутствует для собственного значения +1. Собственные значения −1 интерпретируются как так называемые потоковые анионы на p-пластинках и заряженные анионы на s-пластинках. Таким образом, стабилизирующее пространство кода соответствует анионному вакууму, а анионная конфигурация является синдромом кода.

Также могут быть определены пограничные операторы, которые коммутируют со стабилизаторами. Их можно интерпретировать с точки зрения заполнения ребер энионами, при этом поток энионов соответствует собственному значению -1 левого или правого края, а заряд энионов соответствует собственному значению -1 верха или низа. Занятия ребер определяют состояние логического кубита, хранящегося в коде. Базис X (Z) логического кубита может быть определен так, что | +〉 (| 0〉) соответствует вакууму на верхнем (левом) краю, а | Состояние −〉 (| 1〉) соответствует потоку (заряду) любого иона. Ошибки, воздействующие на спины кода, будут создавать и перемещать энионы и, таким образом, нарушать хранимую информацию, когда они заставляют энионы перемещаться за края. Задача декодирования состоит в том, чтобы удалить энионы таким образом, чтобы ни один чистый энион не сдвинулся с какого-либо края. Логическая ошибка возникает, когда декодирование делает это неправильно.

Создание пар анионных плакеток достигается за счет ошибок переключения битов. Пары вершинных анионов создаются фазовыми переворотами. Таким образом, плакетный и вершинный синдромы кода могут быть исправлены независимо друг от друга. В целом это не даст наилучшего декодирования, но существенно упрощает его. Именно такой подход будет использовать наш декодер. Поскольку два типа синдрома эквивалентны, мы ограничимся плакетками без ограничения общности.

3. Алгоритм декодирования

Задача алгоритма декодирования — найти корректирующий оператор для нейтрализации синдрома. Это означает, что он должен вернуть состояние кода в состояние с тривиальным синдромом. Кроме того, оператор исправления должен также отменить влияние ошибок на сохраненную логическую информацию. Это невозможно сделать с единичной вероятностью. Это можно сделать с высокой вероятностью, с экспоненциальным спадом частоты отказов с размером системы, но успех будет сильно зависеть от конструкции декодера.

В идеале декодер выполнит процесс глобальной оптимизации, чтобы найти оператор исправления, который с наибольшей вероятностью будет успешным, учитывая синдром. Однако такие методы никогда не бывают простыми. Альтернативой является поиск участков синдрома на малых масштабах длины, которые можно нейтрализовать независимо от остальных. Как только все синдромы, с которыми можно справиться в этой шкале, скорректированы, можно рассматривать все более и более высокие шкалы, пока весь синдром не будет нейтрализован. Декодеры, использующие такой итеративный метод, называются декодерами HDRG. См. [5] для общего определения и обсуждения примеров.

Для планарного кода синдром состоит из анионов. Они создаются попарно строками ошибок переключения битов. Таким образом, любая пара анионов может быть нейтрализована независимо от остальной части синдрома, а цепочка переворотов битов служит требуемым оператором исправления.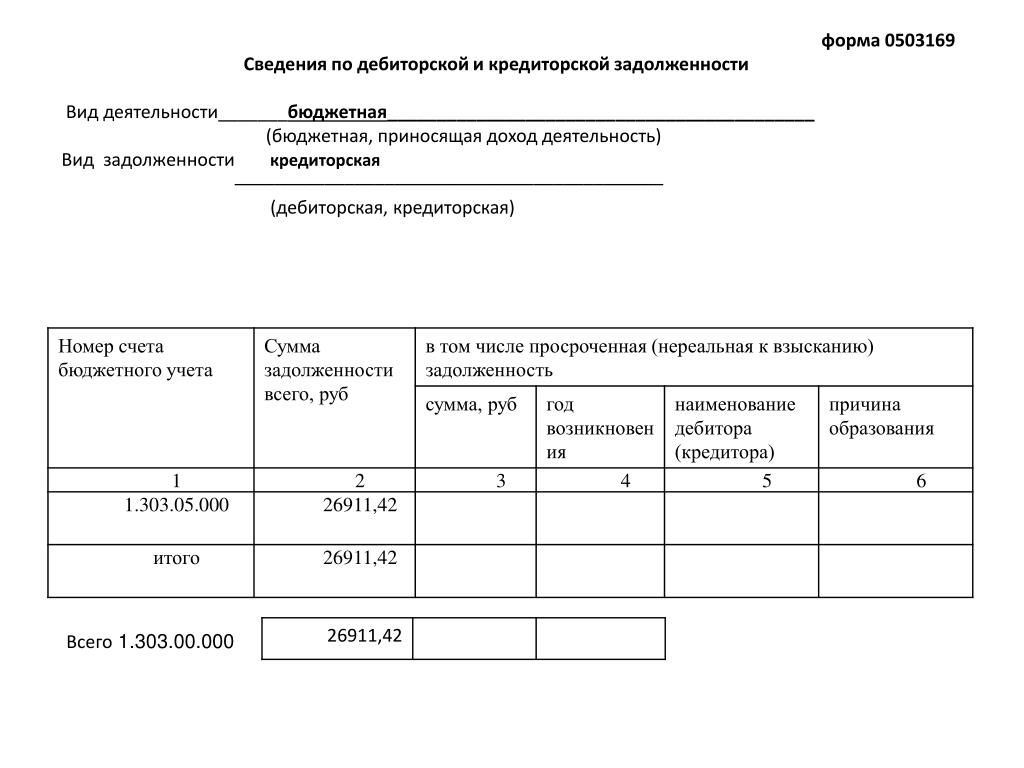 Отдельные анионы также можно нейтрализовать, соединив их с краем. В идеале спаривание, используемое для исправления, такое же, как и для создания, с уничтожением анионов в парах, в которых они были созданы. Это невозможно сделать идеально из-за неоднозначности информации о синдроме. Однако вместо этого мы можем стремиться сделать это с высокой вероятностью. Пока это приводит к правильной четности (нечетной или четной) для количества соединений anyon с каждым ребром, исправление логической информации будет успешным.

Декодер предназначен для поиска пар любых ионов, которые, вероятно, были созданы одной и той же строкой ошибки. Вероятность этого экспоненциально убывает с их разделением. Таким образом, любой, кто является взаимным ближайшим соседом, будет хорошим кандидатом. Таким образом, декодер находит и объединяет таких взаимных ближайших соседей. Для этого используется следующий метод.

Переберите все плакетки, чтобы найти любую.
Для каждого эниона найти все плакетки на манхэттенском расстоянии k, первоначально используя k = 1.
Если на этом расстоянии найден какой-либо элемент или ребро, соедините их. Уничтожьте анионы, выполнив перевороты битов на соединяющих кубитах. Если на этом расстоянии есть несколько возможностей, соедините их с первой найденной.
Если все еще присутствуют какие-либо ионы, повторите процесс для k = k + 1.

После того как все какие-либо ионы будут удалены, рассматривается общая схема битовых переворотов, использованных для их удаления. Процедура исправления считается успешной, если она принадлежит к тому же классу эквивалентности, что и шаблон перестановки битов, произошедший по ошибке. В противном случае процедура исправления приводит к логической ошибке.

Можно легко определить верхнюю границу времени работы в наихудшем сценарии. k-я итерация требует поиска O(k) плакеток на энион. Количество анионов, присутствующих на каждой итерации, не превышает O(L ² ). Итераций будет не более L, так как ни один из них не находится дальше этого расстояния от края. Тогда общая сложность никогда не превышает О(∑k=1LkL2)=O(L4). Эта верхняя граница сложности явно является полиномиальной в зависимости от размера системы, а также полиномом умеренно низкого порядка. Таким образом, алгоритм обеспечивает быстрое и эффективное декодирование.

4. Минимальные требования к логическим ошибкам

Для любого кода и декодера важным критерием производительности является минимальное количество ошибок, необходимое для возникновения логической ошибки. Мы будем использовать ϵ для обозначения значения этого числа, реализуемого исчерпывающим декодером, и ϵ′ для обозначения значения для описанного выше декодера.

Для планарного кода ϵ = L/2 для четного L и (L + 1)/2 для нечетного L. Это минимальное количество переворотов спина, необходимое для создания пары энионов, так что для образования пары требуется меньшее количество переворотов. их с противоположными краями, чем друг с другом. Игнорируя поправки O(1), как мы будем продолжать делать в дальнейшем, мы можем сформулировать это просто как ϵ = L/2.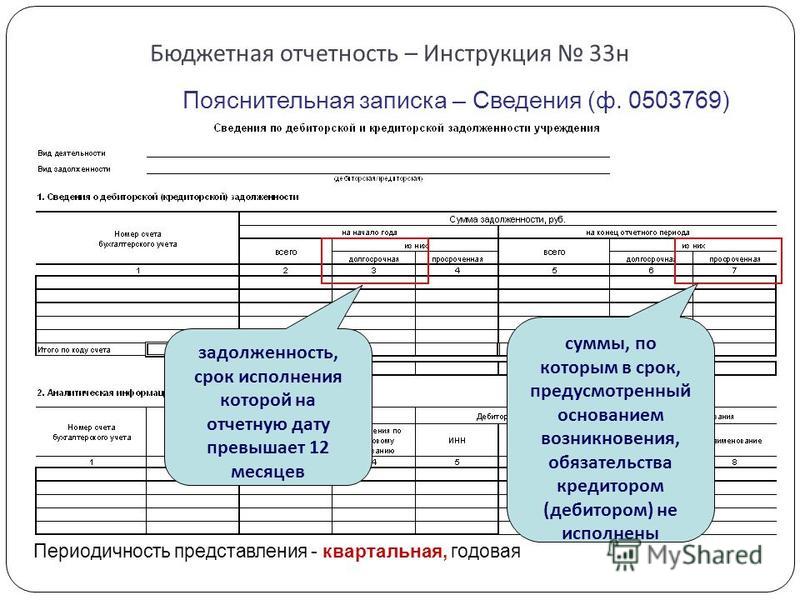

Чтобы найти ϵ′, введем следующую терминологию.

Строка — это совокупность ошибок, в которой в каждой конечной точке существует либо любой, либо ребро.
Кластер — это набор строк, а также соответствующих им конечных точек.
Ширина w кластера — это максимальное расстояние между парой его конечных точек.
Расстояние d между непересекающимися кластерами является минимальным расстоянием между конечной точкой и каждым из них. Говорят, что кластеры перекрываются, если существуют две конечные точки i и j из одного кластера и k из другого такие, что d _ij > d _ik .
Изолированный кластер — это кластер, ширина которого меньше, чем расстояние до любого другого кластера или до края.
Связующий кластер — это кластер, содержащий оба ребра.
Кластер уровня n + 1 — это совокупность кластеров уровня n, каждый из которых находится от другого не дальше своей ширины. Кластер уровня 0 — это одиночная ошибка.

Изолированные кластеры определяются таким образом, что ни один из участников кластера не должен смотреть дальше ширины кластера, чтобы найти ближайшего соседа, прежде чем он будет уничтожен. Кроме того, ни один из членов кластера не будет рассматриваться для создания пары кем-либо извне, пока он не будет уничтожен. Таким образом, алгоритм будет уничтожать анионы в изолированных кластерах друг с другом (или с краем, если он также включен) без ссылки на какие-либо другие.

Учитывая набор ошибок, рассмотреть все кластеры уровня 0. Любой из них, являющийся изолированным кластером, можно игнорировать, не влияя на дальнейший анализ, потому что он не влияет на другие энионы.

По определению, все оставшиеся кластеры уровня 0 будут частью как минимум одного кластера уровня 1. Давайте тогда рассмотрим все возможные кластеры уровня 1. Любой из них, который изолирован, снова будет обрабатываться алгоритмом независимо от остальных, и поэтому его можно игнорировать.

Эту процедуру можно повторять для кластеров более высокого уровня, пока не останется ошибок. Если ни один связующий кластер никогда не рассматривался, алгоритм обязательно исправит ошибки. Следовательно, наличие связующего кластера является необходимым, но недостаточным условием логической ошибки. Определение минимального количества ошибок, необходимых для создания такого связующего кластера, даст нижнюю границу ϵ′.

Для этого ясно, что любые ошибки, которые в конечном итоге будут проигнорированы до того, как кластер станет составным, излишни. Таким образом, нам требуется набор ошибок, ни одна из которых не игнорируется. Таким образом, все кластеры уровня 0 (ошибки) должны быть частью кластера уровня 1, все кластеры уровня 1 частью кластера уровня 2 и так далее.

Рассмотрим равномерный случай, когда каждый кластер уровня n + 1 содержит m кластеров уровня n. Понятно, что для того, чтобы стать охватом как можно быстрее, лучше всего, чтобы все ошибки располагались вдоль одной строки кода. Чтобы сделать каждый кластер уровня 1 максимально длинным, должно быть как можно больше промежутков между m ошибками при сохранении кластера уровня 1. Это будет соответствовать m ошибкам, равномерно распределенным с промежутком в один спин без ошибки между каждым, и, таким образом, всего m — 1 промежутков. Тогда ширина каждого кластера уровня 1 будет равна w ₁ = 2m − 1,

Аналогично, чтобы сделать каждый кластер уровня 2 максимально длинным, должно быть m − 1 пробелов длины w ₁, на которых нет ошибок. Тогда ширина каждого кластера уровня 2 будет равна w ₂ = (2m − 1)w ₁ = (2m − 1) ² . Продолжая таким образом, каждый кластер уровня n будет иметь ширину w _n = (2m − 1) ⁿ . Заметим также, что каждый кластер уровня n будет содержать m ⁿ ошибок.

Минимальное средство для формирования связующего кластера состоит в том, чтобы иметь кластер уровня n, в котором крайняя левая конечная точка находится ближе к левому краю, чем к крайней правой конечной точке, а крайняя правая конечная точка ближе к правому краю чем влево (или то же самое, поменяв местами левый и правый). Первое гарантирует, что кластер не будет изолирован от левого края, а второе гарантирует, что оба объединенных кластера не будут изолированы от правого края. Минимальная ширина кластера уровня n, необходимая для выполнения этого требования, составляет L/4. Для этого требуется кластер уровня n = ln(L/4)/ln(2m − 1). Тогда требуемое количество ошибок равно m ⁿ = (L/4) ^ln ^m ^/ln(2 ^m ⁻¹⁾ . Показатель степени достигает своего минимального значения β = log ₃ 2 ≈ 0,63 для m = 2.

Ясно, что неоднородный случай, когда разные кластеры уровня n+1 могут содержать различное количество кластеров уровня n, не позволит кластеру стать составным с меньшим количеством ошибок. Таким образом, L ^β представляет собой минимальное количество ошибок, необходимое для остовного кластера, и, следовательно, формирует нижнюю границу для ϵ′.

Для верхней границы ϵ′ мы можем найти набор ошибок, которые приводят к сбою алгоритма. Один такой пример может быть построен аналогично приведенному выше. Однако вместо того, чтобы два кластера уровня n внутри кластера уровня n+1 находились на расстоянии w _n друг от друга, мы поместили их друг от друга на расстояние w _n −1. Это приведет к тому, что алгоритм будет постоянно спаривать неправильные anyons, что приведет к логической ошибке.

С учетом этой процедуры легко увидеть, что w _n = 3w _n _-1 — 1 = (3 ⁿ + 1)/2. Для этого требуется кластер уровня n = log ₃ (L/2 − 1) для логической ошибки, и поэтому (L/2 − 1) ^β ошибок. Комбинируя это с нижней границей, мы находим, что ϵ′= (cL) ^β для 1/4 ≤ c ≤ 1/2. Обратите внимание, что это не линейно с L, как хотелось бы в идеале, но его расхождение по степенному закону все равно должно обеспечивать хорошее подавление ошибок, как в примерах, обсуждаемых в [15]. Обратите внимание, что набор найденных здесь ошибок связан с набором Кантора [6,16].

5. Численные результаты для конкретных моделей ошибок

6. Модифицированная метрика расстояния

Представленный здесь алгоритм является примером декодера HDRG. Некоторые свойства этого класса методов декодирования представлены в [5]. Это включает предлагаемое улучшение для этих декодеров, направленное на увеличение минимального количества физических ошибок, необходимых для возникновения логической ошибки.

Предлагаемое улучшение представляет собой переопределение расстояний, используемых декодером. Назначение расстояний состоит в том, чтобы отразить вероятность того, что два элемента синдрома будут конечными точками одной и той же строки ошибки. Таким образом, наиболее очевидным выбором является количество ошибок, необходимое для их исправления, которое представляет собой манхэттенское расстояние для плоского кода, определенного на квадратной решетке. Однако это не всегда приводит к лучшим результатам.

Предположим, что в какой-то итерации процесса декодер решает уничтожить два аниона b и c, разделенных манхэттенским расстоянием D _bc . Затем декодер предполагает, что между ними возникла цепочка ошибок D _bc. На некоторой более поздней итерации декодер должен будет определить, следует ли уничтожить другую пару, a и d. Для этого ему нужно будет знать количество ошибок, которые потребовала бы цепочка ошибок между ними. Обычно это будет манхэттенское расстояние D _{объявление} . Однако рассмотрим путь между a и d, который пересекает c и b. Таким образом, цепочка ошибок, идущая от a к b, а затем от c к d, также будет соответствовать исходному синдрому. Это потребует ошибок D _ab + D _cd, что может быть меньше, чем D _ad в целом. Спаривание a и d тогда будет более вероятным, чем предполагает декодер, из-за возможности этого сокращения для цепочки ошибок.

Улучшение, предложенное в [5], адаптированное для конкретного случая планарного кода, состоит в обновлении расстояний между парами энионов каждый раз, когда происходит аннигиляция. Первоначально расстояние D(a, b) между всеми парами энионов будет равно манхэттенскому расстоянию. При аннигиляции пары c и d расстояния обновляются в соответствии с

Это позволит использовать информацию о синдроме, касающуюся пар, аннигилированных в начале процесса, в дальнейшем, даже если они были удалены из синдрома. Таким образом, декодер может принимать более точные решения относительно того, какие из них следует спаривать на более поздних этапах.

На рисунке 4 представлены данные для сравнения результатов декодера, когда эти переопределенные расстояния используются, с теми, когда они не используются. Они называются «ускоренный» и «стандартный» методы соответственно. Из-за того, как реализован укороченный метод, труднее получить результаты для больших размеров системы. Таким образом, прямое сравнение порогов не проводится. Вместо этого системный размер L ^* сравнивается как для коррелированных, так и для некоррелированных моделей ошибок. Обнаружено, что ярлыки не дают существенных преимуществ при низкой частоте ошибок, для которой соответствующее значение L ^* мало. Однако для более высоких коэффициентов ошибок рост L ^* с p и p’ оказывается намного медленнее, когда используются сокращения, и поэтому такая же степень подавления ошибок может быть достигнута с гораздо меньшими системами.

Также сравнивается коэффициент логических ошибок. Для модели некоррелированных ошибок отношение P(стандарт)/P(сокращения) найдено для p = 3,5% ≈ p _c/2 и системы различных размеров. Это соотношение показывает, насколько выше вероятность неудачи стандартного метода, чем упрощенного. Результаты предполагают, что это экспоненциально увеличивается с L или его степенью. Это говорит о том, что значение β для сокращений выше, чем для стандартного метода, как и ожидалось [5]. Отношение аналогично находится для модели коррелированных ошибок и p′=2,5%≈pc′/2 с аналогичными результатами.

7.

Выводы и перспективы
Представленная здесь стандартная версия декодера очень похожа на «ванильную». Есть много изменений, которые можно было бы внести для улучшения производительности метода, помимо известного примера ярлыков. Например, вместо того, чтобы соединяться с первым любым найденным в каждом случае анионом, можно сравнить все анионы, найденные на одном и том же расстоянии, и сделать осознанный выбор, с кем соединиться. Другой возможностью является усовершенствование метода Монте-Карло цепи Маркова из [8]. Все такие модификации будут зависеть от рассматриваемого кода и модели ошибок. Эта статья предназначена только для демонстрации основного метода, поэтому такие модификации, специфичные для приложения, здесь не изучались.
Несмотря на свою простоту, показано, что метод очень хорошо работает в качестве декодера. Он достигает респектабельных эталонных показателей для стандартного полигона планарного кода с независимым битовым и фазовым шумом: порог аналогичен другим декодерам и теоретическому максимуму; исправление ошибок очевидно для небольших размеров системы; и обнаруживается, что частота логических ошибок сильно уменьшается. Хорошие результаты были также получены для случая пространственно коррелированных ошибок. Таким образом, декодер можно использовать для получения хороших результатов для топологических кодов, а также для более экзотических задач декодирования, прежде чем будут разработаны более сложные индивидуальные методы.
Благодарности
Автор хотел бы поблагодарить Бенджамина Брауна за обсуждения, Эндрю Ландаля за указание на существовавший ранее вариант этого декодера и Swiss NF, NCCR Nano и NCCR QSIT за поддержку.
Конфликт интересов
Автор заявляет об отсутствии конфликта интересов.
Ссылки
Вуттон, Дж. Р. Квантовая память и исправление ошибок. Дж. Мод. Опт 2012 , 20, 1717–1738. [Академия Google]
Вуттон, младший; Бурри, Дж.; Иблисдир, С .; Потеря, Д. Исправление ошибок для неабелевых топологических квантовых вычислений. физ. Rev. X 2014 , 4. [Google Scholar] [CrossRef]
«> Бравый С.; Хаах, Дж. Квантовая самокоррекция в трехмерной модели кубического кода. физ. Rev. Lett 2013 , 111. [Google Scholar] [CrossRef]
Anwar, H.; Браун, Би Джей; Кэмпбелл, ET; Браун, Д.Э. Быстрые декодеры топологических кодов qudit. New J. Phys 2014 , 16. [Google Scholar] [CrossRef]
Хаттер А.; Потеря, Д .; Вуттон, Дж. Р. Улучшенные декодеры HDRG для кудита и неабелевой квантовой коррекции ошибок 2014 . архив: 1410.4478.
Деннис, Э. Очистка квантовых состояний: квантовые и классические алгоритмы 2005 . arXiv: квант-тел/0503169.
Деннис, Э.; Китаев, А.; Ландаль, А .; Прескилл, Дж. Топологическая квантовая память. Дж. Матем. Phys 2002 , 43. [Google Scholar] [CrossRef]
Hutter, A.; Вуттон, младший; Потеря, Д. Эффективный алгоритм Монте-Карло цепи Маркова для поверхностного кода. физ. Версия А 2014 , 89. [Google Scholar] [CrossRef]
Фаулер, А.Г. Оптимальная коррекция сложности коррелированных ошибок в поверхностном коде 2013 . архив: 1310.0863.
Бравый С.; Сучара, М .; Варго, А. Эффективные алгоритмы декодирования с максимальным правдоподобием в поверхностном коде. физ. Rev. A 2014 , 90. [Google Scholar] [CrossRef]
Novais, E.; Муччиоло, Э. Р. Порог кода поверхности при наличии коррелированных ошибок. физ. Ред. Письмо 2013 , 110. [Google Scholar] [CrossRef]
Хаттер, А.; Потеря, Д. Нарушение исправления ошибок поверхностного кода из-за связи с бозонной ванной. физ. Rev. A 2014 , 89. [Google Scholar] [CrossRef]
Fowler, A.G.; Мартинис, Дж. М. Количественная оценка влияния локальных многокубитных ошибок и нелокальных двухкубитных ошибок на поверхностный код. физ. Rev. A 2014 , 89. [Google Scholar] [CrossRef]
«> Китаев А. Отказоустойчивые квантовые вычисления anyons. Анна. Физ 2003 , 303, 2–30. [Google Scholar]
Ковалев А.А.; Прядко Л.П. Отказоустойчивость квантовых разреженных кодов контроля четности с сублинейным масштабированием по расстоянию. физ. Rev. A 2013 , 87. [Google Scholar] [CrossRef]
Landahl, A. (Альбукерке, Нью-Мексико, США). Частное сообщение 2013 .
Дюкло-Чианчи, Г.; Пулен, Д. Быстрые декодеры для топологических квантовых кодов. физ. Rev. Lett 2010 , 104. [Google Scholar] [CrossRef]
Фаулер, А.Г. Точное моделирование плоских топологических кодов не может использовать циклические границы. физ. Версия А 2013 , 87. [Google Scholar] [CrossRef]
Бравый С.; Варго, А. Моделирование редких событий при квантовой коррекции ошибок. физ. Rev. A 2013 , 88. [Google Scholar] [CrossRef]
Рисунок 1. Спиновая решетка планарного кода размера L × L. S-пластинки показаны синим цветом, а p-пластинки показаны белым. В каждой вершине находится частица со спином 1/2. В этом примере линейный размер L = 5. Линейный размер L также является расстоянием кода.
Рисунок 1. Спиновая решетка планарного кода размера L × L. S-пластинки показаны синим цветом, а p-пластинки показаны белым. В каждой вершине находится частица со спином 1/2. В этом примере линейный размер L = 5. Линейный размер L также является расстоянием кода.
Рисунок 2. Результаты для некоррелированных ошибок. ( a ) График частоты логических ошибок, P, в зависимости от частоты ошибок бит-переворота, p, вокруг порога. ( b ) График минимального размера линейной системы, необходимой для P < p, L ^*, против р. ( c ) График P в зависимости от линейного размера системы, L, для различных p значительно ниже порогового значения. ( d ) График зависимости α(p) от p.
Рисунок 2. Результаты для некоррелированных ошибок. ( a ) График частоты логических ошибок, P, в зависимости от частоты ошибок бит-переворота, p, вокруг порога. ( b ) График минимального размера линейной системы, необходимого для P < p, L ^* , по сравнению с p. ( c ) График P в зависимости от линейного размера системы, L, для различных p значительно ниже порогового значения. ( d ) График зависимости α(p) от p.
Рисунок 3. Результаты для коррелированных ошибок. ( a ) График частоты логических ошибок, P, по отношению к частоте ошибок при инверсии битов, p’, около порога. ( b ) График минимального размера линейной системы, необходимого для P < p', L ^*, в зависимости от p’.
Рисунок 3. Результаты для коррелированных ошибок. ( a ) График частоты логических ошибок, P, по отношению к частоте ошибок при инверсии битов, p’, около порога. ( б ) График минимального размера линейной системы, необходимого для P < p', L ^*, в зависимости от p’.
Рисунок 4. Сравнение результатов метода с использованием ярлыков со стандартным методом. ( a ) Графики L ^* в зависимости от p для некоррелированных ошибок с использованием обоих методов. ( b ) Графики L ^* в зависимости от p’ для коррелированных ошибок с использованием обоих методов. ( c ) График зависимости P(стандарт)/P(сокращения) от L как для некоррелированных, так и для некоррелированных ошибок. Для первого данные приведены для p = 3,5%. Для последних это p = 2,5%.
Рисунок 4. Сравнение результатов метода с использованием ярлыков со стандартным методом. ( a ) Графики L ^* в зависимости от p для некоррелированных ошибок с использованием обоих методов. ( b ) Графики L ^* в зависимости от p’ для коррелированных ошибок с использованием обоих методов. ( c ) График зависимости P(стандарт)/P(сокращения) от L как для некоррелированных, так и для некоррелированных ошибок.

Как заполнить форму 0503169: Форма 0503169 для казенных учреждений: как заполнить и сдать?