Корректировка сзв м добавить сотрудника без штрафа: Забыли указать одного сотрудника в СЗВ-М

Корректировка сзв м добавить сотрудника без штрафа: Забыли указать одного сотрудника в СЗВ-М

Корректировка отчета СЗВ-СТАЖ в программных продуктах 1С – Учет без забот

Опубликовано 19.10.2020 16:03

Автор: Administrator

Просмотров: 23607

СЗВ-СТАЖ – форма отчетности, сдаваемая ежегодно не позднее 1 марта года, следующего за отчетным. Ранее мы уже писали о том, как создать первичный отчет СЗВ-СТАЖ. Ведь тут важно не допустить ошибок, т.к. от правильности данных зависит будущая пенсия сотрудников, а неточности в отчете грозят штрафными санкциями. Но на практике без ошибок не бывает. И в случае необходимости исправления уже сданной формы СЗВ-СТАЖ необходимо заполнить новую форму СЗВ-КОРР, предназначенную для корректировки ранее поданных сведений. И всё бы ничего, однако СЗВ-КОРР бывает нескольких видов. О том, какая форма нужна именно вам и как ее создать в программах 1С поговорим сегодня. 

Напоминаем, что отчет по форме СЗВ-СТАЖ подают все плательщики страховых взносов: 

• имеющие наемных работников;

• заключившие трудовые договора или договора гражданско-правового характера, в т.

ч. авторские, по которым

• начисляются страховые взносы и т.д.

В форму СЗВ-СТАЖ включаются сведения и по сотрудникам:

• находящимся в отпуске за свой счет;

• в отпуске по уходу за ребенком;

• в ситуации, когда договор заключен, но оплата не произведена и т.п.

В зависимости от вида ошибки СЗВ-КОРР имеет несколько видов:

• «Корректирующая» — для исправления или уточнения ошибочных сведений. Например, у сотрудника указан неверный период работы;

• «Отменяющая» — отменяет сведения, указанные в форме. Например, в форму включен лишний, уволенный ранее сотрудник, или по ошибке сотрудник указан дважды.

• «Особая» — наоборот, в форму по ошибке не включили сотрудника.

Порядок заполнения формы «Данные о корректировке сведений, учтенных на индивидуальном лицевом счете застрахованного лица (СЗВ-КОРР)» утвержден Постановлением Правления ПФ РФ от 06.12.2018 №507п.

СЗВ-КОРР в программе 1С: ЗУП ред.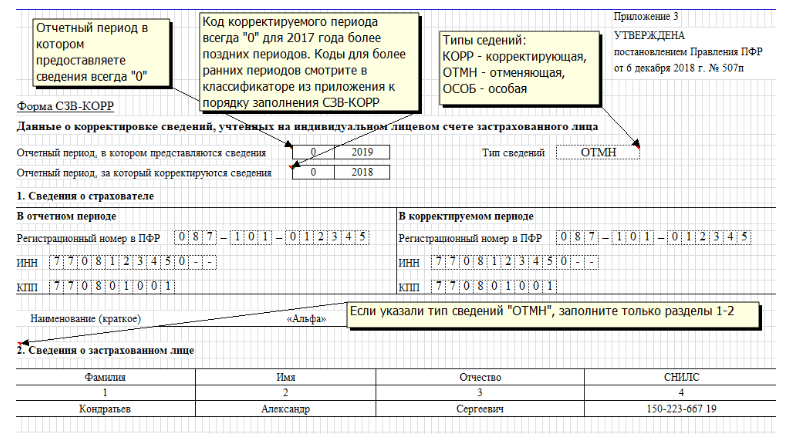 3.1

Итак, форму СЗВ-КОРР можно создать двумя способами.

1 вариант – в разделе «Отчетность, справки» — «1С – Отчетность».

2 вариант – в разделе «Отчетность, справки» — «ПФР. Пачки, реестры, описи».

Рассмотрим создание СЗВ-КОРР в разделе «1С – Отчетность».

Шаг 1. Перейдите в раздел «Отчетность, справки» — «1С-Отчетность».

Шаг 2. Нажмите «Создать» и в окне «Виды отчетов» в разделе «По получателям» из группы «ПФР» выберите «Данные о корректировке сведений застрахованных лиц, СЗВ-КОРР».

Шаг 3. Заполните шапку формы:

• отчетный период;

• корректировочный период;

• тип сведений.

В зависимости от вида исправления укажите тип сведений:

• «Корректирующая»;

• «Отменяющая»;

• «Особая».

Рассмотрим на примерах каждую из корректировок.

СЗВ-КОРР – «Корректирующая».

Для внесения изменений в данные о сотруднике установите «Тип сведений» — «Корректирующая».

Шаг 4. Выберите сотрудника, по которому нужно внести исправление – кнопка «Подбор».

Шаг 5. Щелкните двойным щелчком на строке с сотрудником. В открывшемся окне проверьте сведения о стаже и при необходимости внесите исправления.

После изменения сведений исправленные данные будут выделены жирным шрифтом.

Шаг 6. Нажмите «ОК» и сохраните изменения.

Шаг 7. Сформируйте печатную форму – «кнопка «Печать» — «СЗВ-КОРР».

Форма имеет 6 разделов.

С 1 по 3 раздел – это общие сведения о страхователе и застрахованном лице.

Раздел 4 и 5 содержат сведения о корректировке данных о доходе физлица, начисленных и уплаченных страховых взносах, и страховых взносах по дополнительному тарифу (5 раздел).

Раздел 6 отражает сведения о корректировке периодов работы сотрудника.

В зависимости от типа изменений заполняются соответствующие разделы формы. В нашем примере мы внесли изменения, отражающиеся в 6 разделе СЗВ-КОРР.

Шаг 8. Проведите корректировку. Отправьте ее сразу в контролирующий орган, если используете сервис 1С-Отчетность, либо выгрузите форму в файл по кнопке «Выгрузить» для отправки через сторонние программы.

Во втором случае укажите папку выгрузки. Имя файла программа сформирует автоматически. Нажмите «Сохранить». Файл СЗВ-КОРР в формате *.XML подготовлен к отправке.

Созданная корректирующая форма сохранена. Найти ее можно в разделе «Отчетность, справки» — «ПФР. Пачки, реестры, описи».

СЗВ-КОРР – «Отменяющая».

Рассмотрим пример создания «Отменяющей» СЗВ-КОРР.

Воспользуемся вторым способом создания формы – из журнала «ПФР. Пачки, реестры, описи».

Шаг 1. Нажмите «Создать» и выберите «Данные о корректировке сведений застрахованных лиц, СЗВ-КОРР».

Принцип заполнения формы такой же, как описан выше.

Заполните шапку формы, укажите тип сведений «Отменяющая» и подберите сотрудника, по которому необходимо отменить сведения.

Например, сотрудник Пастухов А.Ф. ошибочно был включен в форму СЗВ-СТАЖ дважды. Формой СЗВ-КОРР отменяется его «дублирующая» запись.

Шаг 2. Выполните проверку формы – «Проверка» — «Проверить выгрузку». Сохраните ее для отправки в папку компьютера – «Выгрузить».

СЗВ-КОРР – «Особая».

Создадим СЗВ-КОРР с типом сведений «Особая».

Пример: При заполнении формы СЗВ-СТАЖ за период 2019 года забыли указать сотрудника Виноградову Г.И.

Шаг 1. В этой ситуации, заполнив шапку формы, указав тип сведений «Особая», добавляем сотрудника в табличную часть документа – формы.

Проверьте сведения о физлице, щелкнув дважды мышкой на строке с сотрудником.

На закладке «Данные по страхователю» можно дополнить данные о начисленных и уплаченных страховых взносах в пенсионный фонд, задолженности на начало или конец периода.

Шаг 2. Сохраните форму, распечатайте или подготовьте файл для отправки в ПФР.

Если вы обнаружили неточность в сданной форме отчетности СЗВ-СТАЖ, не надо ждать пока ПФР укажет на ошибку. Корректирующую форму можно сдать в любой момент при обнаружении ошибки по собственной инициативе.

Так в журнале у нас сохранено три варианта корректирующей формы СЗВ-КОРР.

Одновременно с формой СЗВ-КОРР в пенсионный направляется и опись – ОДВ-1.

Создание СЗВ-КОРР в 1С: Бухгалтерии предприятия ред. 3.0

В программе 1С: Бухгалтерия предприятия ред. 3.0 форма СЗВ-КОРР заполняется аналогично 1С: ЗУП ред. 3.1.

Сделать это можно также 2 способами.

1 вариант – Раздел «Зарплата и кадры» — «ПВР. Пачки, реестры, описи».

Создание и заполнение формы корректировки такое же, как и в программе 1С: ЗУП.

2 вариант – «Отчеты» — «Регламентированные отчеты».

Форма «Данные о корректировке сведений застрахованных лиц, СЗВ-КОРР» находится также в разделе ПФР, при выборе на закладке «По получателям».

Или в разделе «Отчетность по физлицам» на закладке «По категориям».

Форма-документ имеет тот же вид, что и в 1С: ЗУП ред. 3.1.

Как видите, в конфигурациях 1С, формы отчетности создаются и заполняются одинаково. И если вы работали с 1С: ЗУП, вам не составит труда заполнить эту же форму отчета в 1С: Бухгалтерия предприятия.

Автор статьи: Ольга Круглова

Понравилась статья? Подпишитесь на рассылку новых материалов

Добавить комментарий

Как заполнить корректирующий отчет СЗВ-СТАЖ в 2022 году

Челозерцева Александра Юрист по корпоративным вопросам.

8 июля 2022

9701

Распечатать

Поделиться

Размер шрифта:

Если организация отчиталась в ПФР с ошибками, во избежание штрафа сведения необходимо отредактировать. Рассказываем, как заполнить корректировку СЗВ-СТАЖ за 2021 год на примере распространенных ошибок.

Содержание

Почему надо исправлять ошибки

Отчет направляют ежегодно. Данные в нем влияют на размер будущей пенсии, поэтому требования к нему строгие: передаваемые сведения должны отражать достоверную информацию и не содержать недостоверной информации и опечаток. При наличии ошибок в сданной форме их необходимо исправить: как сдать уточненный СЗВ-СТАЖ, зависит от вида ошибки.

В какие сроки исправлять

Закон не содержит срока для сдачи корректировки, их направляют по мере выявления недостоверных данных как организацией самостоятельно, так и сотрудником ПФР. Закон не предусматривает штраф за СЗВ-СТАЖ корректирующий: наказать вправе за несдачу формы или за некорректные данные. Перед назначением наказания ПФР обязан уведомить страхователя об ошибках и запросить корректировку (постановление Арбитражного суда Центрального округа от 20.08.2019 № Ф10-3437/2019). На исправление по запросу ПФР дадут пять дней. Если страхователь выявил их самостоятельно, исправления допустимы в любой момент (п. 40 инструкции, утв. Приказом Минтруда 22.04.2020 № 211н).

Эксперты КонсультантПлюс разобрали, в каких случаях в ПФР предоставляется корректирующая (дополняющая) персонифицированная отчетность. Используйте эти инструкции бесплатно.

Для чтения получите доступ в КонсультантПлюс (бесплатно на 2 дня)

Как исправить данные в отчете

Для исправлений используют отдельную форму — СЗВ-КОРР: как подать корректировку СЗВ-СТАЖ — заполните СЗВ-КОРР с соответствующими данными.

В зависимости от вида исправлений, в форму вносят отметки: «ОТМН», «Особая» или «Дополняющая».

Рассмотрим распространенные ошибки:

Ошибка	Примечание
Не указаны данные: Ф.И.О. или СНИЛС	Графы 3-6 раздела 3 формы обязательны к заполнению. Отчество не указывают, если оно отсутствует в документах гражданина.
Неверно указан СНИЛС	При смене фамилии требуется внесение изменений в СНИЛС. Если фамилия и СНИЛС не совпадают — информация некорректна.
Неверно указан период работы	Период работы указывают в пределах отчетного года, а не всего времени работы в организации — это ошибка.
Периоды стажа указаны не по порядку	Дни указывают последовательно.
Не указали сведения о сотруднике	Отчет направляют по всем работникам, при отсутствии одного или нескольких сотрудников необходимо дополнить отчет.

Добавить или исключить сотрудника

Рассмотрим, как сделать корректировку СЗВ-СТАЖ за 2021 год по одному сотруднику, если сведения о нем не указали или указали ошибочно.

Вариант 1. Исключить сотрудника:

1. Заполняют форму СЗВ-КОРР с указанием в разделе «тип сведений» — «ОТМН».
2. Заполняют первый и второй разделы, остальные — пустые.
3. Вместе с корректировочным направляют ОДВ-1.

Вариант 2. Добавить сотрудника:

1. Заполняют бланк как для первичных сведений.
2. Код «Дополняющая» применяют перед тем как сдать корректировку СЗВ-СТАЖ за 2021 год или за иной прошедший период: ставят галочку в поле «Дополняющая».
3. Вносят достоверные сведения.
4. К исправленному отчету прилагают ОДВ-1.

Исправить Ф.И.О. или СНИЛС

Вот как исправить ошибку в СЗВ-СТАЖ за 2022 год после сдачи в ПФР, по запросу Пенсионного фонда при оформлении гражданину пенсии, если допущены ошибки в Ф.И.О., СНИЛС и пр.:

1. Направьте форму с типом «ОТМН» и исключите сотрудника с ошибками.
2. Подайте дополняющую форму с верными сведениями.

Используйте бесплатно комментарий к постановлению Арбитражного суда Центрального округа от 24. 03.2020 по делу № А14-4671/2019 «Как штрафуют за несдачу отчета СЗВ-СТАЖ» от экспертов КонсультантПлюс, чтобы избежать штрафов.

Для чтения получите доступ в КонсультантПлюс (бесплатно на 2 дня)

Уточнить стаж

Вот как исправить СЗВ-СТАЖ, если неправильный период работы: заполните СЗВ-КОРР с верными данными и направьте в ПФР.

Как передать в ПФР исправленные данные

Исправленные формы направляйте аналогично первичным: по телекоммуникационным каналам связи или нарочно.

Пошаговая инструкция, как в СБИС сделать корректирующий отчет СЗВ-СТАЖ:

Шаг 1. Создайте корректировочный документ.

Шаг 2. Выберите тип отчета.

Шаг 3. Укажите сотрудника и внесите новые данные.

Шаг 4. Готовый документ направьте в ПФР.

‘;}

Распечатать

Поделиться

Челозерцева Александра Юрист по корпоративным вопросам.

В 2017 году окончила НФИ КемГУ по специальности «юриспруденция». Начала работу помощником арбитражного управляющего (банкротство). Спустя 1,5 года перешла в администрацию бизнес-центра на должность руководителя юр. отдела. Сопровождаю бизнес.

Все статьи автора

Вам может быть интересно:

Подписывайтесь на наш канал в Telegram

Мы расскажем о последних новостях и публикациях

Подписаться

Простое руководство по SVM и настройке параметров в Python и R

Введение

Классификация данных — очень важная задача машинного обучения. Машины опорных векторов (SVM) широко применяются в области классификации образов и нелинейных регрессий. Первоначальная форма алгоритма SVM была представлена ​​Владимиром Н. Вапником и Алексеем Я. Червоненкисом в 1963 году. С тех пор SVM претерпели огромные изменения, чтобы успешно использоваться во многих реальных задачах, таких как категоризация текста (и гипертекста), классификация изображений, биоинформатика (классификация белков, классификация рака), распознавание рукописных символов и т. д.

Содержание

1. Что такое метод опорных векторов?
2. Как это работает?
3. Вывод уравнений SVM
4. Плюсы и минусы SVM
5. Реализация Python и R

Что такое метод опорных векторов (SVM)?

Машина опорных векторов — это контролируемый алгоритм машинного обучения, который можно использовать как для задач классификации, так и для задач регрессии. Он следует методу, называемому трюком ядра, для преобразования данных и на основе этих преобразований находит оптимальную границу между возможными выходными данными.

Проще говоря, он выполняет чрезвычайно сложные преобразования данных, чтобы выяснить, как разделить данные на основе определенных меток или выходных данных. В этой статье мы рассмотрим только алгоритм классификации SVM.

Как это работает?

Основная идея состоит в том, чтобы определить оптимальную разделяющую гиперплоскость, которая максимизирует запас обучающих данных. Давайте разберемся в этом объективном термине за термином.

Что такое разделяющая гиперплоскость?

92\)). Но машина опорных векторов может работать и для общего n-мерного набора данных. А в случае более высоких измерений гиперплоскость является обобщением плоскости.

Более формально, это n-1-мерное подпространство n-мерного евклидова пространства. Таким образом, для одномерного набора данных

• одна точка представляет собой гиперплоскость.
• 2D набор данных, линия представляет собой гиперплоскость.
• 3D набор данных, плоскость является гиперплоскостью.
• А в высшем измерении она называется гиперплоскостью.

Мы уже говорили, что цель SVM состоит в том, чтобы найти оптимальную разделяющую гиперплоскость. Когда говорят, что разделяющая гиперплоскость оптимальна?

Тот факт, что существует гиперплоскость, разделяющая набор данных, не означает, что она лучшая.

Давайте поймем оптимальную гиперплоскость с помощью набора диаграмм.

1. Несколько гиперплоскостей
   Существует несколько гиперплоскостей, но какая из них является разделяющей гиперплоскостью? Легко видеть, что линия В лучше всего разделяет два класса.
   
2. Несколько разделяющих гиперплоскостей
   Также может быть несколько разделяющих гиперплоскостей. Как найти оптимальный? Интуитивно, если мы выберем гиперплоскость, близкую к точкам данных одного класса, то это может плохо обобщаться. Таким образом, цель состоит в том, чтобы выбрать гиперплоскость, которая находится как можно дальше от точек данных каждой категории.
   На приведенной выше диаграмме гиперплоскостью, отвечающей заданным критериям оптимальной гиперплоскости, является B.

Следовательно, максимальное расстояние между ближайшими точками каждого класса и гиперплоскостью приведет к оптимальной разделяющей гиперплоскости. Это расстояние называется запасом.

Цель SVM — найти оптимальную гиперплоскость, поскольку она не только классифицирует существующий набор данных, но и помогает предсказать класс невидимых данных. А оптимальная гиперплоскость та, которая имеет наибольший запас.

Математическая настройка

Теперь, когда мы поняли базовую настройку этого алгоритма, давайте погрузимся непосредственно в математические особенности SVM.

Я предполагаю, что вы знакомы с основными математическими понятиями, такими как векторы, векторная арифметика (сложение, вычитание, скалярное произведение) и ортогональная проекция. Некоторые из этих концепций также можно найти в статье Предпосылки линейной алгебры для машинного обучения. 9n \mbox{ и } b \in \mathbb{R}\)

Это делит входное пространство на две части, одна из которых содержит векторы класса ?1, а другая содержит векторы класса +1.

В оставшейся части этой статьи мы будем рассматривать двумерные векторы. Пусть \(\mathcal{H}_0\) будет гиперплоскостью, разделяющей набор данных и удовлетворяющей следующему:

\(\displaystyle\vec{w}.\vec{x}+b=0\)

Наряду с \(\mathcal{H}_0\) мы можем выбрать две другие гиперплоскости \(\mathcal{H}_1\) и \(\mathcal{H}_2\), чтобы они также разделяли данные и имеют следующие уравнения:

\(\vec{w}.\vec{x}+b=\delta\) и \(\vec{w}.\vec{x}+b=\mbox{-}\delta\)

Это делает \(\mathcal{H}_o\) равноудаленными от \(\mathcal{H}_1\), а также от \(\mathcal{H}_2\).

Переменная ? не является необходимым, поэтому мы можем установить ?=1, чтобы упростить задачу как \(\vec{w}.\vec{x}+b=1\) и \(\vec{w}.\vec{x}+b = \mbox{-}1\)

Далее мы хотим убедиться, что между ними нет точки. Поэтому для этого мы выберем только те гиперплоскости, которые удовлетворяют следующим ограничениям:

Для каждого вектора \(x_i\) либо:

1. \(\vec{w}.\vec{x}+b\leq \mbox{-}1\) для \(x_i\) класса ? 1 или
2. \(\vec{w}.\vec{x}+b\geq 1\) для \(x_i\) класса 1

Объединение ограничений

Оба указанных выше ограничения могут быть объединены в одно ограничение.

Ограничение 1:

Для \(x_i\) класса -1, \(\vec{w}.\vec{x}+b\leq \mbox{-}1\)
Умножение обеих сторон на \(y_i\) (что всегда равно -1 для этого уравнения)
\(y_i\left(\vec{w}.\vec{x}+b\right)\geq y_i(-1)\), что подразумевает \(y_i\left(\vec{w}.\vec{x }+b\right) \geq 1\) для \(x_i\) класса?1.

Ограничение 2:  \(y_i=1\)

\(y_i\left(\vec{w}. 2}{2}\) при условии \ ( y_i\left(\vec{w}.\vec{x}+b\right) \geq 1 \mbox{ для любого } i=1,\dots, n \)

Это случай, когда наши данные линейно разделимы. Есть много случаев, когда данные не могут быть идеально классифицированы с помощью линейного разделения. В таких случаях машина опорных векторов ищет гиперплоскость, которая максимизирует запас и минимизирует ошибки классификации.

Для этого мы вводим переменную slack,\(\zeta_i\), которая позволяет некоторым объектам выходить за пределы поля, но наказывает их.

В этом сценарии алгоритм пытается поддерживать переменную резерва равной нулю, максимально увеличивая запас. Однако он минимизирует сумму расстояний ошибочной классификации от граничных гиперплоскостей, а не количество ошибочных классификаций. 92}{2}+C\sum_i\zeta_i\) при условии \( y_i\left(\vec{w}.\vec{x}+b\right) \geq 1-\zeta_i \mbox{ для любого } i =1,\dots, n \)

Здесь параметр \(C\) является параметром регуляризации , который управляет компромиссом между штрафом переменной резерва (ошибки классификации) и шириной поля.

• Маленький \(C\) позволяет легко игнорировать ограничения, что приводит к большому запасу.
• Большой \(C\) позволяет игнорировать жесткие ограничения, что приводит к небольшому запасу.
• Для \(C=\inf \) применяются все ограничения.

Самый простой способ разделить два класса данных — это линия в случае 2D-данных и плоскость в случае 3D-данных. Но не всегда возможно использовать линии или плоскости, и для разделения этих классов требуется нелинейная область. Машины опорных векторов обрабатывают такие ситуации, используя функцию ядра, которая отображает данные в другое пространство, где линейная гиперплоскость может использоваться для разделения классов. Это известно как 92}{2} + C\sum_i\zeta_i \) при условии \(y_i(\vec{w}.\phi(x_i)+b)\geq 1-\zeta_i\) \( \mbox{ для всех } 1 \leq i \leq n, \zeta_i\geq 0\)

Мы не будем вдаваться в решение этих оптимизационных задач. Наиболее распространенным методом, используемым для решения этих задач оптимизации, является выпуклая оптимизация.

Плюсы и минусы машин опорных векторов

Каждый алгоритм классификации имеет свои преимущества и недостатки, которые проявляются в зависимости от анализируемого набора данных. Вот некоторые из преимуществ SVM:

• Сама природа метода выпуклой оптимизации гарантирует гарантированную оптимальность. Решение гарантированно является глобальным минимумом, а не локальным минимумом.
• SVM — это алгоритм, который подходит как для линейно, так и для нелинейно разделяемых данных (с использованием трюка ядра). Единственное, что нужно сделать, это придумать член регуляризации, \(C\).
• SVM хорошо работают как с небольшими, так и с многомерными пространствами данных. Он эффективно работает для многомерных наборов данных из-за того, что сложность обучающего набора данных в SVM обычно характеризуется количеством опорных векторов, а не размерностью. Даже если убрать все остальные обучающие примеры и повторить обучение, мы получим ту же оптимальную разделяющую гиперплоскость.
SVM
• могут эффективно работать с небольшими обучающими наборами данных, поскольку они не полагаются на все данные.

Недостатки SVM заключаются в следующем:

• Они не подходят для больших наборов данных, поскольку время обучения с помощью SVM может быть большим и требует больших вычислительных ресурсов.
• Они менее эффективны для более зашумленных наборов данных с перекрывающимися классами.

SVM с Python и R

Давайте посмотрим на библиотеки и функции, используемые для реализации SVM на Python и R.

Реализация Python

Наиболее широко используемой библиотекой для реализации алгоритмов машинного обучения в Python является scikit-learn. Класс, используемый для классификации SVM в scikit-learn: svm.SVC()

sklearn.svm.SVC (C=1.0, kernel=’rbf’, Degree=3, gamma=’auto’)

Параметры следующие: :

• C: Это параметр регуляризации C члена ошибки.
Ядро
• : указывает тип ядра, который будет использоваться в алгоритме. Это может быть «линейный», «полигональный», «rbf», «сигмоидальный», «предварительно вычисленный» или вызываемый. Значение по умолчанию — «rbf».
Степень
• : это степень полиномиальной функции ядра («поли»), которая игнорируется всеми другими ядрами. Значение по умолчанию – 3 
.
• gamma: это коэффициент ядра для «rbf», «poly» и «sigmoid». Если для гаммы установлено значение «авто», вместо этого будет использоваться 1/n_features.

Есть много дополнительных параметров, которые я здесь не обсуждал. Вы можете проверить их здесь.

https://gist.github.com/HackerEarthBlog/07492b3da67a2eb0ee8308da60bf40d9

Можно настроить SVM, изменив параметры \(C, \gamma\) и функцию ядра. Функция настройки параметров, доступных в scikit-learn, называется gridSearchCV().

sklearn.model_selection.GridSearchCV(estimator, param_grid)

Параметры этой функции определены как:

• оценка: это объект оценки, который в нашем случае является svm. SVC().
• param_grid: Это словарь или список с именами параметров (строка) в качестве ключей и списками настроек параметров, которые можно попробовать использовать в качестве значений.

Чтобы узнать больше о других параметрах GridSearch.CV(), щелкните здесь.

https://gist.github.com/HackerEarthBlog/a84a446810494d4ca0c178e864ab2391

В приведенном выше коде параметрами, которые мы рассмотрели для настройки, являются ядро, C и гамма. Значения, из которых должно быть наилучшее значение, указаны в скобках. Здесь мы дали только несколько значений для рассмотрения, но для настройки может быть задан целый диапазон значений, но это займет больше времени для выполнения.

R Реализация

Пакет, который мы будем использовать для реализации алгоритма SVM в R, называется e1071. Используемая функция будет svm().

https://gist.github.com/HackerEarthBlog/0336338c5d93dc3d724a8edb67ad0a05

Резюме

В этой статье я дал очень простое объяснение алгоритма классификации SVM. Я не упомянул несколько математических сложностей, таких как расчет расстояний и решение задачи оптимизации. Но я надеюсь, что это дало вам достаточно знаний о том, как алгоритм машинного обучения, то есть SVM, может быть изменен в зависимости от типа предоставленного набора данных.

Методы опорных векторов в машинном обучении (SVM): руководство 2023 г. Акцент сместился с фундаментальных математических вопросов о простой линейной регрессии и логистической регрессии на более продвинутые алгоритмы машинного обучения.

Одна из таких популярных моделей, приемлемая для вычислений и дающая отличные результаты, — это машины опорных векторов в машинном обучении.

Модель, которая используется для классификации, а также регрессии, фундаментальные знания о регрессии опорных векторов и классификации должны быть известны всем энтузиастам Data Science. В этой статье мы рассмотрим алгоритм SVM или машинное обучение SVM, чтобы узнать больше о том, как моделировать работы в деталях, чтобы вы могли добавить алгоритм машины опорных векторов в свой набор инструментов Data Science. Посетите неполный учебный курс по науке о данных, чтобы лучше понять машины опорных векторов в машинном обучении.

Что такое машины опорных векторов (SVM) в машинном обучении?

Модель SVM или модель Support Vector Machine — это популярный набор моделей обучения с учителем, которые используются для регрессионного и классификационного анализа. Это модель, основанная на структуре статистического обучения, известная своей надежностью и эффективностью во многих случаях использования. Основываясь на невероятностном бинарном линейном классификаторе, машина опорных векторов используется для разделения разных классов с помощью различных ядер.

Одна из основных причин, по которой компании склоняются к моделям машин опорных векторов по сравнению с другими моделями, заключается в том, что машины опорных векторов обладают значительно более высокой точностью, которую можно использовать при меньшем количестве вычислений из системы. Здесь следует отметить один небольшой момент: приложения SVM обычно реализуются в области классификации.

Вопрос о том, какое ядро ​​выбрать при выполнении минимальных вычислений, огромен, особенно когда мы имеем дело с большими наборами данных. Это делается с помощью так называемого «трюка с ядром». Мы подробно рассмотрим эту тему в следующем разделе. Давайте сначала получим представление о машинах опорных векторов, рассмотрев несколько примеров.

Почему SVM используются в машинном обучении?

Две основные причины, по которым машины опорных векторов используются в машинном обучении:

• Относительно высокая точность. Одним из основных преимуществ машины опорных векторов является то, что по сравнению с более фундаментальными алгоритмами она имеет гораздо более высокую относительную точность. . Это означает, что при развертывании модели в реальном мире мы видим лучшие результаты от реализованных моделей машинного обучения.
• Минимальное время вычислений: благодаря «хитрости ядра» время вычислений машин опорных векторов SVM сокращается, а это означает, что мы, специалисты по данным, можем получать лучшие результаты за меньшее время, используя меньше ресурсов. Это беспроигрышный вариант, поскольку мы можем получить лучшие результаты, не влияя на затраты на использование оборудования, и даже быстрее.

Типы алгоритма опорных векторов

В этом разделе мы узнаем больше о типах SVM на основе типа данных, которые мы используем. Это более конкретно для классификации, поскольку это основной вариант использования для машин опорных векторов.

1. Линейный SVM

Алгоритм машины линейных опорных векторов используется, когда у нас есть линейно разделимые данные. Говоря простым языком, если у нас есть набор данных, который можно разделить на две группы с помощью простой прямой линии, мы называем его линейно разделимыми данными, а используемый для этого классификатор называется линейным классификатором SVM.

2. Нелинейный SVM

Алгоритм нелинейного метода опорных векторов используется, когда у нас есть нелинейно разделимые данные. Говоря простым языком, если у нас есть набор данных, который нельзя разделить на две группы с помощью простой прямой линии, мы называем его нелинейными разделимыми данными, а используемый для этого классификатор называется нелинейным классификатором SVM.

Гиперплоскость и опорные векторы в алгоритме SVM

В этом разделе мы обсудим больше гиперплоскости и опорных векторов в SVM:

1.  Гиперплоскость 

При заданном наборе точек может быть несколько способов разделить классы в n-мерном пространстве. То, как работает SVM, преобразует данные более низкого измерения в данные более высокого измерения, а затем разделяет точки. Существует несколько способов разделения данных, и их можно назвать границами принятия решений. Однако основная идея классификации SVM заключается в том, чтобы найти наилучшую возможную границу решения. Гиперплоскость — это оптимальная, обобщенная и наиболее подходящая граница для классификатора машины опорных векторов.

Например, в двумерном пространстве, как показано в нашем примере, гиперплоскость будет прямой линией. Напротив, если данные существуют в трехмерном пространстве, то гиперплоскость будет существовать в двух измерениях. Хорошее эмпирическое правило заключается в том, что для n-мерного пространства гиперплоскость обычно имеет n-1 измерение.

Цель состоит в том, чтобы создать гиперплоскость с максимально возможным запасом для создания обобщенной модели. Это указывает на максимальное расстояние между точками данных.

2.  Опорные векторы  

Термин опорный вектор указывает, что у нас есть опорные векторы к главной гиперплоскости. Если у нас есть максимальное расстояние между опорными векторами, это указывает на наилучшее соответствие. Таким образом, опорные векторы — это векторы, которые проходят через точки, ближайшие к гиперплоскости, и влияют на общее положение гиперплоскости.

Как найти правильную гиперплоскость?

Теперь мы подходим к важному вопросу: как найти правильную гиперплоскость? Давайте попробуем визуализировать и понять два способа, которыми мы находим правильную гиперплоскость: 

1. Максимальное расстояние между опорными векторами  

Рекомендуемый способ найти правильную гиперплоскость — максимизировать расстояние между опорными векторами. Ниже мы визуализируем, как это будет выглядеть в двумерном пространстве, это можно сделать и в n-мерном пространстве, но визуализировать нам будет сложно.

2. Преобразование данных более низкого измерения в данные более высокого измерения  

Когда мы преобразуем данные более низкого измерения в данные более высокого измерения, с помощью созданных новых функций он разделяет точки в более высоком измерении, и мы можем затем передайте гиперплоскость с большей эффективностью, чтобы отделить данные.

Это делается с помощью следующих шагов:

1. Дополнить данные некоторыми нелинейными функциями, вычисленными с использованием существующих функций
2. Найти разделяющую гиперплоскость в многомерном пространстве
3. исходное пространство

Как SVM работает в машинном обучении?

SVM работает по принципу максимизации расстояния между опорными векторами. Это гарантирует, что у нас будет максимально возможная разница между точками, что дает нам обобщенную модель. Цель классификации машины опорных векторов состоит в том, чтобы максимизировать разницу между опорными векторами. Вы можете узнать больше о SVM в машинном обучении на учебном курсе по науке о данных.

1. Линейно разделимые данные

Мы используем ядра в машинах опорных векторов. Ядра SVM — это функции, на основе которых мы можем преобразовать данные, чтобы было легче подобрать гиперплоскость для лучшего разделения точек.

Линейно разделимые точки состоят из точек, которые можно разделить простой прямой линией. Линия должна иметь максимально возможный запас между ближайшими точками, чтобы сформировать обобщенную модель SVM.

2. Нелинейные данные

Нелинейные данные — это данные, которые нельзя разделить простой прямой линией. Мы можем разделить классы, сопоставив данные с пространством более высокого измерения, чтобы мы могли классифицировать точки. Здесь мы используем производные функции более высокого измерения из самого набора данных. Например, с набором данных, представленным на осях X и Y, мы будем использовать такие функции, как X2, Y2 и XY, чтобы создать модель более высокого измерения, спроецировать данные, создать гиперплоскость, а затем вернуть данные к их исходному состоянию. оригинальное пространство.

Это делается с помощью хитрого трюка, который мы обсудим в следующем разделе. В конце концов, рисунок будет выглядеть так, как показано на рисунке ниже, разделяя два класса в одном и том же исходном пространстве.

3. Уловка с ядром

Уловка с ядром — это «суперсила» машин опорных векторов. Машина опорных векторов использует ядра, ls, которые представляют собой функцию, на основе которой можно разделить точки. Точки, которые не могут быть разделены линейно, являются проекциями в пространство более высокого измерения.

В. Итак, в чем здесь «хитрость»?  

A. SVM представляет нелинейные точки данных таким образом, что точки данных преобразуются, а затем находят гиперплоскость. Однако точки остались прежними, и они не были преобразованы.

Этот трюк является причиной того, что кажущееся преобразование точек из более низкого измерения в более высокое известно как трюк с ядром.

Функции ядра SVM

Мы уже давно говорим о ядрах SVM. Давайте кратко рассмотрим некоторые важные функции ядра, которые помогают преобразовывать данные, чтобы передавать гиперплоскости для разделения данных. Все хитрые приемы, о которых мы говорим, — это математика; преобразования данных выполняются с использованием линейной алгебры. Сейчас мы немного углубимся в математику, так как это поможет вам получить представление о ядре.

1. Функция линейного ядра

Линейное ядро ​​в основном используется для линейно разделимых данных. Он используется для точек, которые имеют линейную зависимость.

2. Функция полиномиального ядра

Функция полиномиального ядра используется путем использования скалярного произведения и преобразования данных в n-мерное. Это помогает представлять данные с более высокой размерностью, используя недавно преобразованные точки данных.

3. RBF (Функция радиального базиса)

Это одна из наиболее распространенных и широко используемых функций в качестве ядра, которая ведет себя аналогично взвешенной модели ближайшего соседа. Он может преобразовывать данные в бесконечные измерения, а затем использовать взвешенную модель ближайшего соседа для определения наблюдений, которые оказывают наибольшее влияние на новую точку данных для классификации. «Радиальная» функция в RBF может быть либо Лапласом, либо Гауссовой. Мы можем решить это на основе гиперпараметра «Гамма».

4. Сигмовидная функция

Сигмовидная функция встречается в таких случаях использования, как нейронные сети, где она используется в качестве функции активации (Tanh). Она также известна как функция гиперболического тангенса и имеет определенные варианты использования, в которых она может лучше разделять данные.

Так объяснялась машина опорных векторов. Теперь мы узнали о различных ядрах, которые используются в функциях машины опорных векторов. Далее мы рассмотрим код Python-классификатора SVM.

Простой классификатор SVM [шаг за шагом]

В этом разделе мы рассмотрим реализацию SVM на Python. Мы быстро рассмотрим пример кода Python, чтобы увидеть, как работает машина опорных векторов. Это контролируемый алгоритм обучения, который используется для выполнения классификации и может быть найден в научном наборе для обучения. Мы можем рассмотреть два варианта использования набора данных с линейным и нелинейным распределением для этой демонстрации Python.

from sklearn.svm import svc # «Классификатор опорных векторов»

Шаг 2: импорт требуемого набора данных

Как правило, в этом случае мы должны импортировать требуемый набор данных, выполнить необходимые шаги предварительной обработки, а затем проанализировать и визуализировать данные. Здесь, в этом случае, мы создадим два больших двоичных объекта, чтобы подчеркнуть мощь машин опорных векторов с использованием ядер, которые мы обсуждали в предыдущих разделах.

Кроме того, наш набор данных будет выглядеть примерно так, где мы хотели бы продемонстрировать линейное разделение данных.

Теперь, если бы мы использовали линейный дискриминационный классификатор, мы попытались бы найти оптимальную прямую линию между двумя наборами данных, чтобы мы могли разделить наборы данных. Существуют различные линии, которые можно провести для разделения наборов данных.

Не знаете, что выбрать? Помните, что мы обсуждали в предыдущих разделах? Наша цель — максимизировать маржу. В следующем разделе мы обсудим именно это.

Шаг 3. Максимизируйте маржу 

Теперь нам нужно подогнать машину линейных опорных векторов, чтобы мы могли построить оптимальную гиперплоскость, чтобы получить наилучшую модель. В этом случае мы будем использовать линейное ядро, так как точки на осях X и Y имеют линейную связь.

Мы используем линейное ядро ​​в классификаторе опорных векторов (svc) из пакета обучения Sciket для надлежащего разделения наборов данных. Цель разделительной границы решения состоит в том, чтобы максимизировать разницу между различными группами точек. Некоторые точки касаются линии и указываются отдельно. Эти точки являются критическими и называются опорными векторами. Они хранятся в атрибуте support_vectors_ функции.

Шаг 4. Подгонка машинного классификатора опорных векторов

На основе настройки гиперпараметров необходимо решить, какой будет наилучшая возможная модель для данного набора данных. Здесь мы замечаем опорные векторы, и положение прямой разделительной линии (называемой гиперплоскостью для n-мерных данных) будет меняться в зависимости от того, как можно максимизировать поля.

В зависимости от параметров и количества строк в обучающих и тестовых данных положение и точность модели SVM будут различаться.

Шаг 5. Определите тип ядра на основе типа распределения данных

На основе распределения данных возможно также нелинейное распределение набора данных, которое можно решить с помощью других ядер. Например, если бы мы использовали линейное ядро ​​для набора данных с нелинейным распределением, мы бы увидели график, похожий на следующий.

Если бы мы проецировали и преобразовывали двумерные данные в трехмерное пространство, это выглядело бы следующим образом.

Здесь, в этом случае, если бы мы использовали ядро ​​​​RBF, график выглядел бы так, как показано на изображении ниже, где мы успешно разделили и сопоставили гиперплоскость обратно с исходными точками.

В этом разделе мы успешно рассмотрели некоторый простой код Python для создания соответствующих наборов данных и показали, как можно использовать машины опорных векторов для создания достаточно точных моделей с минимальными вычислениями с использованием трюка с ядром. В следующем разделе мы рассмотрим некоторые приложения машин опорных векторов, которым также можно научиться на лучших онлайн-курсах по науке о данных.

Применение SVM с гиперпараметрами по умолчанию

Вернемся к примеру и применим SVM после предварительной обработки данных с гиперпараметрами по умолчанию.

1. Линейное ядро ​​

 из sklearn import svm
svm2 = svm.SVC (ядро = «линейный»)
svm2 

 SVC(C=1.0, cache_size=200, class_weight=Нет, coef0=0.0,
solution_function_shape='ovr', степень=3, гамма='авто', ядро='линейный',
max_iter=-1, вероятность=ложь, random_state=нет, сжатие=истина,
tol=0,001, verbose=False)  

 модель2 = svm2.fit(x_train_sc, y_train)
y_pred2 = svm2.predict(x_test_sc)
print('Оценка точности')
print(metrics.accuracy_score(y_test,y_pred2)) 

 Показатель точности:0,9707602339181286 

2. Гауссовское ядро ​​

 svm3 = SVM.SVC(kernel='rbf')
svm3   

 SVC(C=1,0, cache_size=200, class_weight=Нет, coef0=0,0,
solution_function_shape='ovr', степень=3, гамма='авто', ядро='rbf',
max_iter=-1, вероятность=ложь, random_state=нет, сжатие=истина,
tol=0,001, verbose=False)   

 модель3 = svm3. fit(x_train_sc, y_train)
y_pred3 = svm3.predict(x_test_sc)
print('Оценка точности')
print(metrics.accuracy_score(y_test, y_pred3))  

 Показатель точности:0,935672514619883   

3. Полиномиальное ядро ​​

 svm4 = SVM.SVC(kernel='poly')
svm4 

 SVC(C=1.0, cache_size=200, class_weight=Нет, coef0=0.0,
solution_function_shape='ovr', степень=3, гамма='авто', ядро='поли',
max_iter=-1, вероятность=ложь, random_state=нет, сжатие=истина,
tol=0,001, verbose=False)  

 модель4 = svm4.fit(x_train_sc, y_train)
y_pred4 = svm4.predict(x_test_sc)
print('Оценка точности')
print(metrics.accuracy_score(y_test,y_pred4)) 

 Показатель точности:0,6198830409356725   

Как настроить параметры SVM?

1. Ядро

Ядро в машине опорных векторов отвечает за преобразование входных данных в требуемый формат. Некоторые из ядер, используемых в машинах опорных векторов, представляют собой линейные, полиномиальные и радиальные базисные функции (RBF). Чтобы создать нелинейную гиперплоскость, мы используем RBF и полиномиальную функцию. Для сложных приложений следует использовать более продвинутые ядра для разделения нелинейных классов. С помощью этого преобразования вы можете получить точные классификаторы.

2. Регуляризация

Используя параметры C Scikit-learn и корректировку, мы можем поддерживать регуляризацию. C обозначает штрафной параметр, представляющий ошибку или любую форму неправильной классификации. Эта неправильная классификация позволяет вам понять, насколько допустима ошибка. Это поможет вам аннулировать компенсацию между неправильно классифицированным термином и границей решения. При меньшем значении C вы получаете гиперплоскость с небольшим запасом, а при большем значении C получается гиперплоскость с большим значением.

3. Гамма

Меньшее значение Гаммы создает слабую подгонку обучающего набора данных. С другой стороны, высокое значение гаммы позволяет модели лучше соответствовать. Низкое значение гаммы позволит учитывать только близлежащие точки для расчета отдельной плоскости. Однако высокое значение гаммы будет учитывать все точки данных для расчета окончательной разделительной линии.

Примеры SVM

В. Какова основная цель алгоритма классификации?

Основной целью модели классификации в машинном обучении является эффективное разделение различных классов точек и их обобщение. Когда это делается в двумерной (2-D) плоскости, это означает рисование прямой линии, чтобы мы могли линейно разделить два класса точек таким образом, чтобы будущие точки также имели высокую вероятность точного разделения точек.

Используя приведенный ниже пример машины опорных векторов, мы также введем некоторые новые термины: 

Давайте разберемся с простой терминологией:

1. Гиперплоскость: Подобно тому, как линия может разделять точки в двумерном пространстве, гиперплоскость — это плоскость, разделяющая точки в n-мерном пространстве.
2. Положительная гиперплоскость: Пунктирная линия, которую мы видим на рисунке, расположенная в положительной области, называется положительной гиперплоскостью. Положительная гиперплоскость проходит через первую точку положительного пространства.
3. Негативная гиперплоскость: Пунктирная линия, которую мы видим на рисунке, расположенная в отрицательной области, называется отрицательной гиперплоскостью. Отрицательная гиперплоскость проходит через первую точку отрицательного пространства.
4. Hard Margin показывает, что модель SVM очень хорошо работает с набором данных и может привести к переоснащению. Это используется в линейно разделимых данных, только в линейно разделимых данных.
5. Мягкая маржа указывает, что модель является гибкой с точки зрения подбора набора данных и поэтому не вызовет переобучения. Это используется в большинстве случаев, когда данные не являются линейно разделимыми. Это допускает некоторую степень неправильной классификации, чтобы модель лучше подходила к тестовому набору данных.
6. Гиперплоскость максимальной маржи: граница решения (обозначенная на рисунке выше сплошной линией) — это граница решения, на основе которой точки разветвляются.

Идея выбора границы решения заключается в том, что чем больше запас (разница между положительной гиперплоскостью и отрицательной гиперплоскостью), тем меньше ошибка обобщения, поскольку, когда у нас меньшие поля с границами решения, это имеет тенденцию приводить к переоснащению. .

Помимо этого простого, но эффективного примера, машина опорных векторов используется для выполнения более сложных задач, таких как категоризация текста, классификация изображений и даже обнаружение лиц.

Применение машины опорных векторов

В этом разделе мы рассмотрим некоторые варианты использования машин опорных векторов:

• Классификация электронной почты. является спамом или ветчиной На изображении ниже мы видим набор обучающих данных. Кроме того, на изображении ниже мы видим тестовый набор данных, где текст красного цвета указывает на то, что изображение было неверно предсказано.

Мы также можем получить такие показатели, как точность, отзыв и оценка f1.

• Категоризация текста. Категоризация как индуктивных, так и трансдуктивных моделей используется для обучения и использует разные оценки, сгенерированные для сравнения с пороговым значением.
• Распознавание рукописного ввода: SVM также может использоваться для распознавания рукописного ввода, когда мы можем преобразовывать рукописный текст в машиночитаемый текст.
• Биоинформатика: включает классификацию рака и классификацию белков, где мы используем SVM для определения классификации пациентов и генов на основе биологических маркеров.

Преимущества и недостатки метода опорных векторов

В этом разделе мы рассмотрим преимущества и недостатки метода опорных векторов:

Преимущества метода опорных векторов различных классов, SVM работает хорошо.

Эффективность использования памяти является одним из ключевых преимуществ SVM, поскольку он использует подмножество точек обучения как часть опорных векторов функции принятия решений).

SVM имеет тенденцию быть оптимизированным алгоритмом, когда данные существуют в многомерном пространстве.

Хорошо работает, когда количество столбцов превышает количество строк.

Можно использовать различные функции ядра для улучшения моделей.

Недостатки SVM  

• SVM позволяет достичь лучших результатов с меньшими размерами наборов данных, поскольку большие наборы данных могут занять больше времени.
• Нам нужно знать, что при наличии большого количества функций нам нужно избегать переобучения данных, а регуляризация терминов имеет решающее значение.
• Из-за уловки ядра SVM работает, проецируя данные в более высокое измерение, поэтому для выполнения классификации нет вероятностного объяснения. Это можно сделать, но при этом используется пятикратная перекрестная проверка, требующая больших вычислительных ресурсов.

Заключение

Машина опорных векторов (SVM) — это машина, которая контролируется для изучения алгоритмов, используемых как для классификации, так и для регрессии. Цель алгоритма SVM — найти гиперплоскость в N-мерном пространстве, которая четко классифицирует точки данных. В этом блоге мы рассмотрели сквозные вопросы, которые будут заданы на собеседовании. Мы узнали об уловке ядра и поняли различную терминологию, связанную с машинами опорных векторов.

Мы также рассмотрели несколько простых примеров кодирования и то, как можно увеличить прибыль с помощью опорных векторов. Вы можете пройти неполный учебный курс по науке о данных от KnowledgeHut, если хотите получить отличное трудоустройство.

Часто задаваемые вопросы (FAQ)

1. Что такое машины опорных векторов с примерами?

Машина опорных векторов — это набор моделей обучения с учителем, которые можно использовать как для классификации, так и для регрессии. Он хорошо работает с многомерными данными и имеет довольно высокую точность и минимальное время вычислений, особенно с небольшими обучающими наборами данных. К сожалению, он не дает вероятностной оценки баллов. Он используется для линейно и нелинейно разделяемых данных и используется в таких случаях, как классификация электронной почты, категоризация текста, обнаружение лиц и распознавание рукописного ввода.

2. Классификатором какого типа является SVM?

SVM — это классификаторы с максимальным запасом по сравнению с некоторыми другими алгоритмами, такими как наивный байесовский классификатор, который является вероятностным классификатором. Помимо этого, есть и другие функции ядра, которые мы можем использовать.

3. Что лучше, SVM или нейронная сеть?

В зависимости от варианта использования необходимо выбрать модель. Время прогнозирования для нейронных сетей быстрее, чем SVM. Обработка параметров SVM увеличивается линейно с увеличением размера входных данных. Во многих случаях нейронные сети работают лучше, но могут требовать больших вычислительных ресурсов.

4. Каковы преимущества SVM?

У SVM есть множество преимуществ. Он имеет лучшую эффективность памяти и хорошо работает с многомерными данными (где количество столбцов больше, чем количество строк).