Квантум системс вход в личный кабинет: Как войти в личный кабинет Quantum System
Регистрация — Quantum System
1 ШАГ : Создайте учетную запись Quantum System прямо сейчас
Нажимая «Получить доступ», вы подтверждаете, что ознакомились и полностью понимаете Правила Пользования системой «Quantum System» и выражаете свое согласие с ними.
Зарегистрируйтесь
Создайте учетную запись
Получите доступ к программе
Готово!
Получайте прибыль!
МЫ ОТВЕТИМ НА ВАШИ ВОПРОСЫ И ПОМОЖЕМ ЗАРАБОТАТЬ ДЕНЬГИ
Что такое Quantum System?
Quantum System – это 100% БЕСПЛАТНАЯ программа, которая может торговать на рынках бинарных опционов в 1 клик! Она полностью автоматизирована и выбирает для Вас выигрышные сделки!
Сколько я могу зарабатывать с помощью этой программы?
Если в двух словах, то без границ.
Каков минимальный депозит?
Естественно, Вам нужно внести деньги на свой торговый счет, прежде чем Вы сможете получать прибыль. Помните, что для того, чтобы начать зарабатывать деньги, нужны деньги. Вам необходимо внести на депозит КАК МИНИМУМ $250, но чем больше Вы внесете с самого начала, тем больше денег Вы заработаете сразу же! Помните, что Вы легко заработаете эти деньги в первый же день + даже больше! И Вы сможете снять эти деньги, когда захотите! Лично я бы порекомендовал Вам начать с $500 или больше, но $250 тоже будет неплохо!
Как начать зарабатывать?
Есть несколько простых шагов, которые нужно сделать, прежде чем начать зарабатывать деньги. 1 шаг: посмотрите видео и зарегистрируйтесь, чтобы получить доступ к Quantum System! 2 шаг: Создайте учетную запись (аккаунт) у нашего рекомендуемого брокера, чтобы Вы смогли торговать.
Нужно ли мне использовать кредитную карту для регистрации?
НИ В КОЕМ СЛУЧАЕ!. Программа Quantum System является 100% БЕСПЛАТНОЙ. Вам не нужна кредитная карта, счет в WebMoney или другая банковская информация при загрузке Quantum System! После того, как Вы зайдете в личный кабинет, мы порекомендуем Вам брокера бинарных опционов, которым Вы сможете пользоваться. Чтобы начать получать прибыль, Вам нужно внести деньги на депозит. Это ВАШИ деньги, которые вы просто вносите для того, чтобы торговать, и Вы можете снять их, когда захотите!
ЗАРЕГИСТРИРУЙТЕСЬ ВЫШЕ, ЧТОБЫ НАЧАТЬ ПРЯМО СЕЙЧАС!
Отзывы о «Квантум систем» Евгения Абрамова
Каждому бы хотелось жить в свое удовольствие, пока деньги делаются сами из воздуха.
Только одни не верят в басни и достигают все своим трудом, а другие постоянно ищут способ легкого обогащения. Именно для таких мечтателей в интернете уже несколько лет гуляет проект Quantum System, который бесплатно предлагает полностью автоматизированную систему для заработка на бинарных опционах. Сегодня мы расскажем всю правду об этой программе, если вы еще не поняли, развод это, или нет.
Вас обманули? В 80% случаев все деньги можно вернуть!
Посмотрите видео, где практикующий юрист, который когда-то сам потерял крупную сумму на Форексе, нашел выход! С коллегами он основал компанию по возврату средств у людей, обманутых нелицензированными компаниями-мошенниками. Если Вы потеряли деньги на бинарных опционах из-за действий «брокера» — смотрите видео, заполняйте форму ниже. Ребята помогают!
Не откладывайте: Запускайте процедуру возврата ВАШИХ денег! Действуйте БЫСТРО — так шансы на возврат всей сумма возрастают МНОГОКРАТНО!
Можете попробовать сделать это самостоятельно, но опытные юристы уже, скорее всего, вернули деньги Вашим собратьям по несчастью.
Действуйте быстро, пока есть еще, что возвращать — мошенники долго ждать не будут, и выведут деньги, спрячут их по «офшорам» или обналичат. Тогда будет точно поздно…
Подробнее о компании Юникорн Чарджбек.
Как работает Quantum System?
Итак, Quantum System Management – это компания, которая появилась в Рунете в 2016 году с революционной, по ее утверждению, автоматической торговой системой получения дохода онлайн 24 часа в сутки и 7 дней в неделю. Генеральным директором компании является некий Евгений Александрович Абрамов, который якобы разработал эту систему вместе с IT-специалистами еще в 2006 году, работая на инвестиционной фирме в Москве. Примечательно, что этот проект является копией американского варианта The Quantum Code, который фактически не отличается даже сценарием завлекательного видеоролика.
Сайт Квантум Систем
Первое, что видит человек, попавший на сайт Quantum System – это 45 минутный видеоролик, в котором Евгений Абрамов обещает, что с его торговой системой абсолютно любой человек может зарабатывать от 5 до 40 тысяч американских долларов в день.
Больше на сайте ничего нет, кроме контактов в виде электронной почты, клиентского соглашения и навязчиво появляющейся формы для регистрации. Видео нельзя перемотать или вернуться назад на несколько минут. Можно только поставить на паузу или начать смотреть сначала.
В своем рекламном ролике Абрамов выступает неким добрым волшебником-мультимиллионером из списка Форбс, который каждому желающему хочет абсолютно бесплатно подарить «виртуальную машинку для печати денег». Видео рассчитано на то, чтобы максимально впечатлить человека – вертолет, красавица помощница, Macbook, скрин с личного банковского счета, где уже 15 миллионов долларов, и постоянный акцент в разговоре на крупные суммы, которые ежедневно зарабатывают тысячи пользователей Quantum System.
Также не менее десяти раз утверждается, что это на 100% гарантированный способ ежедневного получения прибыли, работающий без потерь и проигрышей. Кроме того, постоянно подчёркивается эксклюзивность данной разработки и ограниченное количество свободных мест для тех, кто может воспользоваться бесплатным предложением для бета-тестирования новой версии программы.
В чем «фокус» программы?
По утверждениям ее разработчиков, система выполняет расчеты на сумасшедших скоростях, являясь крутым программным обеспечением, которое ни разу не ошиблось с 2006 года. Система использует точную секретную формулу, основанную на квантовых вычислениях, которая дополняется отсутствием в работе человеческого фактора. Ее принцип работы заключается в анализе рынков всех биржевых активов одновременно, и автоматическом заключении сделки еще до того момента, как это успеет сделать любой «живой» трейдер на планете. И все это только благодаря колоссальной скорости вычисления, безупречной работе и концептуальной формуле.
После 20-ти минут рассказов о том, как система Квантум может помочь каждому стать финансово независимым, разговор плавно переходит к трейдингу. Абрамов предлагает не тратить годы на изучение финансовых рынков, ведь самому даже не нужно будет торговать. Нужно будет только открыть торговый счет у одного из брокеров-партнеров, синхронизировать свой аккаунт с аккаунтом в Quantum System, и просто запустить программу в авторежиме.
Затем, со слов Абрамов, можно сесть поудобней и расслабиться, ведь это техническое изобретение будет самостоятельно торговать бинарными опционами, да еще и без единого убытка. Для этого на сайте настойчиво появляется такая вот форма:
Что такое Quantum System на самом деле
А теперь перейдем от сказки к реальности. Простыми словами – перед вами обычная алгоритмическая программа с сомнительной эффективностью, которую до безумия «распиарили» и сделали средством отъема денег у доверчивой аудитории (которые в последствии не так-то просто вернуть). Первое, что хотят от вас мошенники – чтобы вы зарегистрировались на сайте, оставив в анкете ваше имя и имейл. Дальше вас постоянно будут «прессовать» письмами с предложениями выбрать одного из брокеров и пополнить у него счет на сумму от $250 – это минимум, с которого начинает работать программа. То есть, вы как бы ничего за программу не платите, а просто инвестируете в трейдинг определенную сумму, которую должна увеличить программа (а на самом деле слить).
Кто такой Евгений Абрамов?
Этот персонаж является вымышленным, так как нигде нет подтверждения его реального существования, не говоря уже о списке Forbs. Все это можно запросто проверить, воспользовавшись поисковой формой журнала Форбс и просто интернет-поисковиком. То есть, Евгений Абрамов – это бренд, а реальное имя сыгравшего в рекламе актера неизвестно.
Также вы не найдете информацию о проекте Quantum System в финансово-инвестиционных и технических журналах, о которых несколько раз упоминал Абрамов. Даже о самой компании Quantum System Management, которая по утверждениям является одной из самых крупных в России, нет никакой информации в СМИ.
Выводы
Проект Quantum System Management – это, возможно, мошенники, которые наживаются на тех, кто ищет легкий способ заработка, или просто поверил в существование чудо-робота, торгующего без убытков. Никаких 100% прибыли, никаких гарантий, никакого Евгения Абрамова – все это очень похоже на дешевое представление, скопированное из ранее существовавшего англоязычного варианта.
Поэтому от указанной программы лучше всего держаться подальше. Тем более что на бинарных опционах можно реально зарабатывать, торгуя «вручную». Но если вы все-таки «купились» на красивую историю и уже успели потерять свои деньги с помощью Quantum System, специалисты из компании Юникорн Кешбек помогут Вам их вернуть. Просто заполните форму выше и получите консультацию по Вашей ситуации.
Отзывы о Quantum System
Только правда! Мы размещаем все мнения, если в них нет нецензурной лексики и с-п-а-м-а (форма для отзывов внизу).
Узнайте, что пишут другие трейдеры… Развод или нет? Вас обманули?
1 минута Вашего времени может помочь сотням людей!
Вы просматриваете: Отзывы о Quantum System
Сверху показатьНовыеСтарыеПолезныеБесполезныеПоложительныеОтрицательные
3/5 (4)
Страница 1 из 1
Написать отзыв
Доступ к программе пользователя квантовых вычислений (QCUP) — Документация пользователя OLCF
Добро пожаловать! Информация ниже знакомит с тем, как мы структурируем проекты и
учетных записей для доступа к ресурсам Quantum в рамках программы QCUP.
Чтобы получить доступ, вы должны сначала отправить проектное предложение в OLCF QCUP (см. Распределение по проектам) или присоединиться к существующему проекту QCUP (см. Учетные записи пользователей). Совет по использованию квантовых ресурсов (QRUC), а также независимые судьи, рассматривают и утверждают все проектные предложения QCUP. Заявки на QCUP принимаются круглый год через форму заявки на участие в проекте, которую можно найти ниже. Когда проект одобрен, то все пользователи, связанные с проектом, необходимо подать заявку на учетную запись пользователя. После вашей учетной записи пользователя одобрен, вы можете перейти к доступу к квантовым ресурсам, предлагаемым наших поставщиков (см. Доступ к квантовым ресурсам).
Приоритеты QCUP
Программа Quantum Computing User Program в OLCF преследует несколько общих целей:
- Включить исследования
Целью QCUP является обеспечение широкого спектра доступа пользователей к лучшим доступные системы квантовых вычислений.
После того, как предполагаемое исследование пользователя было проверены на предмет достоинств и заключены пользовательские соглашения, мы стремимся предоставить пользователям возможность ознакомиться с уникальными аспектами и проблемы квантовых вычислений, а также для реализации и тестирования квантовых алгоритмы на имеющихся системах.
После того, как предполагаемое исследование пользователя было
проверены на предмет достоинств и заключены пользовательские соглашения, мы стремимся
предоставить пользователям возможность ознакомиться с уникальными аспектами
и проблемы квантовых вычислений, а также для реализации и тестирования квантовых
алгоритмы на имеющихся системах.- Оценка технологии
Целью QCUP является помощь в оценке технологий путем мониторинга широта и производительность первых приложений квантовых вычислений. Как пользователи интегрировать квантовые вычисления с научными вычислениями — вопрос, ограниченный как приложением, ограничениями инфраструктуры, так и вариантами использования, ожидаемыми для связанная вычислительная система. С помощью программы QCUP пользователи могут исследовать новые потенциальные приложения для вычислительных исследований и, возможно, ускорить существующие научные приложения с помощью квантовых процессоров и архитектуры.
Поддерживаемые исследовательские проекты включают передовые научные вычислительная техника, фундаментальная энергетика, биологические исследования окружающей среды, высокоэнергетические физика, наука об энергии синтеза и ядерная физика, среди прочего.
- Вовлечь сообщество
Целью QCUP является привлечение сообщества квантовых вычислений и поддержка рост экосистем квантовой информатики. Наши квантовые вычисления пользователи имеют опыт квантовых вычислений от новичка до эксперта; пользователи из национальных лабораторий США, университетов, правительства и промышленности. Группы пользователей использовать опыт квантовых вычислений для исследования различных приложений интересы, использование нескольких языков программирования, квантово-классическое программирование, и несколько программных сред. Большинство проектов ориентированы на доказательство принципа демонстрации и/или разработка новых методов. Некоторые проекты ориентированы на производительность приложений и/или бенчмаркинг, а также некоторые проекты сосредоточиться на характеристике устройства, проверке и валидации.
Отчисления на проект
Предложение QCUP описывает характер, методологию и достоинства проекта, объясняет, почему для этого требуется доступ к ресурсам QCUP, и описывает любые другие важную информацию, которая может потребоваться для его рассмотрения. Проект заявки подаются с использованием формы заявки проекта. Выберите «OLCF Квантовый Computing User Program» из выпадающего меню.
Для проектов QCUP все предлагаемые работы должны быть открытыми, фундаментальными исследованиями и не Можно использовать экспортный контроль, PHI или другие контролируемые данные.
После отправки вы получите уведомление по электронной почте об успешном предложении подчинение. Затем предложение рассматривается отделом использования квантовых ресурсов. Совета (QRUC), а также независимых судей за заслуги и для обеспечения осуществимость успеха проекта с использованием ресурсов, доступных для QCUP. Ты будет уведомлен о решении QRUC по электронной почте.
Что происходит после утверждения заявки на проект?
После того, как запрос на проект будет одобрен QRUC, менеджер по работе с клиентами OLCF
связаться с PI проекта, чтобы завершить активацию и запросить подписанный
Необходимо предоставить соглашение с главным исследователем.
Затем OLCF установит проект QCUP и уведомит PI о его создании. вместе с 6-значным идентификатором проекта OLCF QCUP и распределением ресурсов подробности. В это время участники проекта могут приступить к подаче заявок на получение индивидуальные учетные записи пользователей.
Продление проекта
QCUP Проекты имеют конечную продолжительность; при запуске проекты получают сколько угодно
месяцев остается в этом периоде распределения, а затем должен быть продлен на
последующие 6-месячные интервалы. Проекты можно продлевать, заполнив продление
форма ( Форма обновления счетов ) и
отправив его по электронной почте на адрес [email protected].
Закрытие и квартальные отчеты
Все проекты QCUP должны представлять ежеквартальные отчеты и отчет о закрытии. Эти формы можно отправить по электронной почте на адрес [email protected].
Учетные записи пользователей
Любой соавтор утвержденного и активированного проекта OLCF может подать заявку
для учетной записи пользователя, связанной с этим проектом, чтобы получить доступ.
Примечание
PI проекта не получают учетную запись пользователя с проектом создание, и должны также применяться.
- Новые пользователи должны подать заявку на учетную запись, используя Запрос учетной записи. Форма. Вам понадобится правильный 6-символьный идентификатор проекта из вашего PI.
- Когда наша команда по работе с клиентами начнет обработку вашей заявки, вы получите автоматизированный электронное письмо, содержащее уникальный 36-значный код подтверждения. Обратите на это внимание; вы можете использовать это, чтобы проверить статус вашего приложения в любое время.
- Главный исследователь (PI) проекта должен одобрить ваш доступ к учетной записи и системе. Мы сообщим PI проекта о вашем запросе.
- Как только ваша заявка будет рассмотрена и одобрена, вы получите уведомление по электронной почте о своей учетной записи. создания, и поставщик квантовых ресурсов свяжется с инструкциями по предоставлению вам доступа.
Доступ к квантовым ресурсам
В отличие от создания личной учетной записи через каждого отдельного
веб-сайты поставщиков, OLCF приобрела подписку на услуги этих поставщиков и
управляет настройкой вашего доступа к каждому из них после того, как ваше пользовательское приложение Quantum
одобрено.
Вы получите индивидуальные приглашения по электронной почте от Quantinuum и
Rigetti с дальнейшими инструкциями, тогда как для IBM вы можете перейти непосредственно к
их веб-сайт для создания учетной записи. Более подробная информация для получения доступа к каждому
поставщика указаны ниже. Для получения подробной информации о том, как использовать систему поставщика один раз
доступ получен, см. наши руководства по квантовым системам
вместо.
IBM Quantum Computing
После подачи заявки на квантовую учетную запись OLCF и получения одобрения,
перейдите на https://quantum-computing.ibm.com/ и нажмите «Создать IBMid
счет». Электронная почта вашей учетной записи IBM Quantum Hub будет электронной почтой, связанной с
вашей учетной записи OLCF. Если войти не удается, свяжитесь с нами по адресу [email protected]. После входа в систему
пользователи получат доступ к IBM Quantum Hub, онлайн-платформе IBM для
Доступ к QPU, форумы для обсуждения квантовых вычислений и т. д. От IBM Quantum
Hub Dashboard, пользователи могут управлять резервированием системы, просматривать систему (бэкэнд)
статусы и просматривать результаты ваших прошлых заданий.
Больше информации об использовании
эти квантовые ресурсы IBM можно найти в документации IBM.
или наш OLCF IBM Quantum Guide.
Quantinuum
После подачи заявки на квантовый счет OLCF и получения одобрения,
вы получите электронное письмо от Quantinuum с приглашением создать свой квантовый
счет. После входа в систему пользователи получат доступ к пользовательскому интерфейсу Quantinuum,
https://um.qapi.quantinuum.com, их онлайн-платформа для управления вакансиями и
доступ к доступным квантовым системам, включая модель системы h2, через
облако. В пользовательском интерфейсе пользователи могут просматривать состояние системы и предстоящую доступность системы,
а также контролировать пакетные представления и историю заданий. Информация об использовании
квантовые ресурсы через блокноты Jupyter доступны в пользовательском интерфейсе через «Примеры»
вкладка Системы Quantinuum обеспечивают измерение промежуточных цепей и повторное использование кубитов.
совместимость с различными программными платформами.
Rigetti
После подачи заявки на квантовый счет OLCF и получения одобрения,
вы получите электронное письмо от [email protected] с приглашением создать свой
квантовый счет. Если вы не получили это, перейдите к
https://qcs.rigetti.com/sign-in и нажмите «Войти». Необходимо, чтобы
электронная почта, которую вы используете для входа, должна быть связана с аффилированной подпиской
организации, т. е. ORNL, ANL и т. д. Если войти не удается, свяжитесь с нами по адресу [email protected].
После входа в систему пользователи получат доступ к Quantum Cloud Services (QCS),
Онлайн-платформа Rigetti для доступа к гибридной инфраструктуре доступных
квантовые процессоры и классическая вычислительная среда через облако. От
QCS пользователи могут просматривать состояние и доступность системы, инициировать и управлять
резервирование квантовой инфраструктуры (выполнение программ вручную или
добавить их в очередь). Информация об использовании этого ресурса доступна на
документацию Ригетти или нашу
Руководство OLCF Ригетти.
Цитаты публикаций
Публикации с использованием ресурсов, предоставленных OLCF, должны включать следующее заявление о подтверждении: «Это исследование использовало ресурсы Дуба Вычислительный центр Ridge Leadership Computing Facility, который является пользователем Управления науки Министерства энергетики. Объект поддерживается по контракту DE-AC05-00OR22725».
Эргодическая динамика и термализация в изолированной квантовой системе
Представьте молекулы воздуха в комнате. Они движутся со всеми возможными скоростями во всех направлениях. Достижение точного знания этих траекторий является сложной и нереальной задачей. Однако статистическая механика утверждает, что точное знание отдельных траекторий не требуется, и системы можно точно описать, используя лишь несколько параметров. Какое существенное свойство этих систем допускает такое простое описание?
Эргодическая динамика объясняет эту простоту. Если динамика эргодическая, то система будет равномерно исследовать все микроскопические состояния с течением времени, ограничиваясь только законами сохранения.
Эргодичность гарантирует, что
, где O — любая макроскопическая наблюдаемая, а скобки обозначают усреднение. В пределе множества частиц макроскопические наблюдаемые, такие как давление или плотность, приближаются к равновесию и стационарны, поэтому в любой момент времени O ( т ) = 〈 О 〉 время . Эти два уравнения подразумевают, что макроскопические наблюдаемые можно предсказать путем равномерного усреднения по всем состояниям, и это составляет основу для всех термодинамических расчетов.
В классических системах именно хаотическое движение заставляет систему эргодически исследовать пространство состояний 5 . Однако квантовые системы подчиняются уравнению Шредингера, которое является линейным и, следовательно, запрещает хаотическое движение 6 . Это ставит фундаментальные вопросы относительно применимости статистической механики к изолированным квантовым системам 9.0123 1,2,3,4 . Проявляют ли квантовые системы эргодичное поведение в смысле уравнения (1)? Действуют ли квантовые системы как собственная ванна для достижения теплового равновесия? Были предприняты обширные экспериментальные усилия для решения этих фундаментальных вопросов 7,8,9,10,11,12,13 .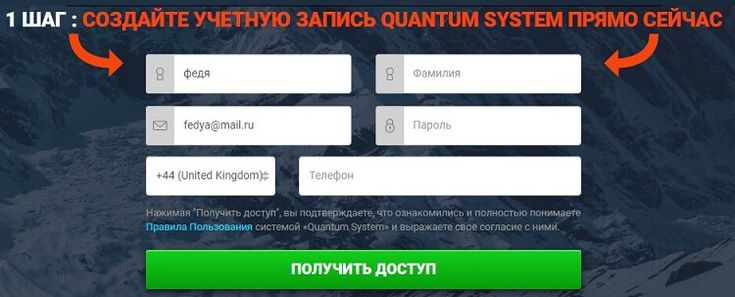
Здесь мы исследуем эргодическую динамику, рассматривая простую квантовую модель, классическим пределом которой является хаотическая 14,15,16,17,18 . Эта модель описывает набор частиц со спином 1/2, коллективное движение которых эквивалентно движению одного большего спина с полным угловым моментом j подчиняется гамильтониану
, где J y и J z — операторы углового момента. Сумма по дельта-функциям подразумевает N применений J z 2 , каждое с целыми временными шагами. Операторы углового момента могут быть выражены через составные операторы Паули со спином 1/2, например, J z = ( ℏ /2)∑ i σ z ( i ) . Установив τ = 1, первый член заставляет каждый спин поворачиваться вокруг оси y на угол π/2. Второй член связывает каждое вращение с каждым другим вращением с силой κ /2 j .
Это можно увидеть, расширив J z 2 с помощью операторов z , где такие термины, как σ z (1) σ z (2) и все другие комбинации появляются.
Классическая динамика, будучи простой для визуализации и интерпретации, может дать ценную интуицию для изучения квантового предела. Классический предел этой модели имеет место, когда j очень велико и эффекты квантования становятся незначительными. В этом пределе система ведет себя как классический волчок с известной хаотической 9 динамикой.0123 14,15,16,17 . Параметр κ задает хаотичность и изменяет динамику с регулярной на хаотическую по мере увеличения κ ; при промежуточных значениях система демонстрирует богатую смесь как регулярного, так и хаотического движения.
Экспериментальная реализация этой модели требует высокой степени контроля как над локальными условиями, так и над взаимодействиями в многокубитном гамильтониане.
Это привело к разработке трехкубитного кольца планарных трансмонов с настраиваемой связью между кубитами (см. Дополнительную информацию) 19,20,21 . Вращения вокруг оси y ( J y ) выполняются с помощью сформированных микроволновых импульсов, резонансных с переходом кубита. Одновременное и симметричное взаимодействие трех кубитов ( J z 2 ) включается и выключается с помощью настраиваемой схемы связи, управляемой тремя отдельными прямоугольными импульсами. Энергия кубит-кубитного взаимодействия g и длительность импульсов взаимодействия T установить κ через соотношение κ = 3 gT / ℏ . Мы измеряем силу энергии взаимодействия κ , определяя время, необходимое для переключения возбуждения между кубитами (см. Дополнительную информацию).
Периодический характер позволяет нам записать унитарную эволюцию за один цикл как
, схематично показанную на рис.
1а. Начнем с инициализации каждого кубита в состоянии
, где θ 0 и φ 0 — углы, описывающие ориентацию однокубитных состояний. Это состояние известно как спиново-когерентное состояние и является наиболее классическим спиновым состоянием в смысле минимальной неопределенности и нулевой запутанности. Подготовив начальное состояние, мы поворачиваем каждый кубит вокруг оси y на угол π/2. Затем мы позволяем всем кубитам взаимодействовать друг с другом в течение времени, которое устанавливает значение κ . Повторяем эти два шага N раз, а затем томографически реконструировать полученную матрицу плотности 22 . Подробнее о последовательности импульсов см. в разделе «Дополнительная информация».
Рис. 1. Последовательность импульсов и результирующая квантовая динамика. a , последовательность импульсов, показывающая сначала начальное состояние трех кубитов (уравнение (4)), за которыми следуют унитарные операции для одного временного шага (уравнение (3)).
Эти операции повторяются N раз перед измерением. Вращения одного кубита генерируются с помощью сформированных микроволновых импульсов длительностью 20 нс; взаимодействие трех кубитов генерируется с помощью перестраиваемой схемы связи, управляемой прямоугольными импульсами длительностью 5 нс в течение κ = 0,5 и 25 нс для κ = 2,5. b , Состояние одного кубита измеряется с помощью томографии состояния и отображается в сфере Блоха. Начальное состояние показано красным цветом, а последующие состояния показаны синим цветом для N = 1–20.
Изображение полного размера
Мы визуализируем эволюцию системы, изображая состояние одного кубита в виде вектора внутри блоховской сферы, показанной на рис. 1b. Каждый вектор Блоха строится путем измерения ожидаемых значений x , y и z операторы Паули после эволюции системы согласно уравнению (3). Поскольку динамика симметрична при обмене кубитами, кубиты претерпевают номинально идентичную эволюцию, и мы строим среднее поведение (см.
Дополнительную информацию). Выбранное начальное состояние показано красным цветом, а вектор Блоха после последующих шагов показан синим цветом. После каждого шага происходят два качественных изменения: поворот и изменение длины. Ориентация аналогична ориентации классического спина. Однако изменение длины описывает запутанность кубитов.
Запутанность можно охарактеризовать с помощью энтропии запутанности S ,
, где ρ sq — матрица плотности одного кубита. Запись следа в виде суммы воспроизводит знакомое определение энтропии −∑ p i log( p i ), где p i равно вероятности того, что 9 в i микросостояние. Если кубит находится в чистом состоянии, то состояние одного кубита полностью известно, а энтропия равна нулю. Однако если кубиты запутаны друг с другом, то ρ sq представляет собой статистическую смесь состояний, а энтропия не равна нулю.
На рис. 2а мы показываем энтропию запутанности между одним кубитом и остальными кубитами в несколько моментов времени. Энтропия запутанности измеряется путем томографии состояния отдельных кубитов 22 и последующего прямого применения уравнения (5) к реконструированной матрице плотности. В каждой панели мы готовим различные начальные состояния | θ 0 , φ 0 〉, развернуть систему на N шагов и построить энтропию запутанности; разные панели соответствуют разным N . Начальные состояния, приготовленные вблизи оси y , имеют низкую энтропию (красный цвет), которая остается низкой по мере развития системы. Состояния, подготовленные дальше от оси y , получают более высокую энтропию (синий цвет) при наличии достаточного времени. Мы проводим ту же серию экспериментов для более сильного взаимодействия, κ = 2,5, как показано на рис. 2b. При более сильных взаимодействиях энтропия быстро возрастает, и области с низкой энтропией больше не изолированы вблизи и -ось.
a , b , Энтропия запутанности (цвет) одного кубита (см. уравнение (5)), усредненная по кубитам и отображенная на сетке 31 × 61 начального состояния, для различных временных шагов N и два значения силы взаимодействия κ = 0,5 ( a ) и κ = 2,5 ( b ). Энтропия запутанности одного кубита может варьироваться от 0 до 1. c , Энтропия запутывания, усредненная по 20 шагам для κ = 0,5 и по 10 шагам для κ = 2,5; для обоих экспериментов максимальная длительность последовательности импульсов составляет ≈ 500 нс. Левая/правая асимметрия является результатом экспериментальных несовершенств и отсутствует в численном моделировании (см. Дополнительную информацию). d , Стробоскопическая карта классической динамики вычислена численно и показана для сравнения. Карта создается путем случайного выбора 5000 начальных состояний, распространения каждого состояния вперед с использованием классических уравнений движения и отображения ориентации состояния после каждого шага в виде точки.
Мы наблюдаем четкую связь между областями хаотического поведения (классического) и высокой энтропии запутанности (квантового).
Изображение в полный размер
На рис. 2а, б мы видим, что энтропия флуктуирует во времени. В небольших квантовых системах существуют флуктуации или возрождения, которые исчезают, когда размер системы доводится до бесконечности (термодинамический предел). Для конечных систем усреднение энтропии по времени обычно используется для оценки равновесного значения, к которому приближаются более крупные системы. На рис. 2c мы показываем усредненную по времени энтропию запутанности ( N ) для обоих значений силы взаимодействия к . Соответствующая классическая динамика показана на рис. 2d.
Мы находим поразительное сходство между средней запутанностью в квантовой системе и хаотической динамикой в классическом пределе. Области классического фазового пространства, где динамика хаотична, соответствуют высокой энтропии (синий цвет) в квантовой системе; области, которые являются классически регулярными, соответствуют низкой энтропии (красный цвет), включая бифуркацию при больших κ .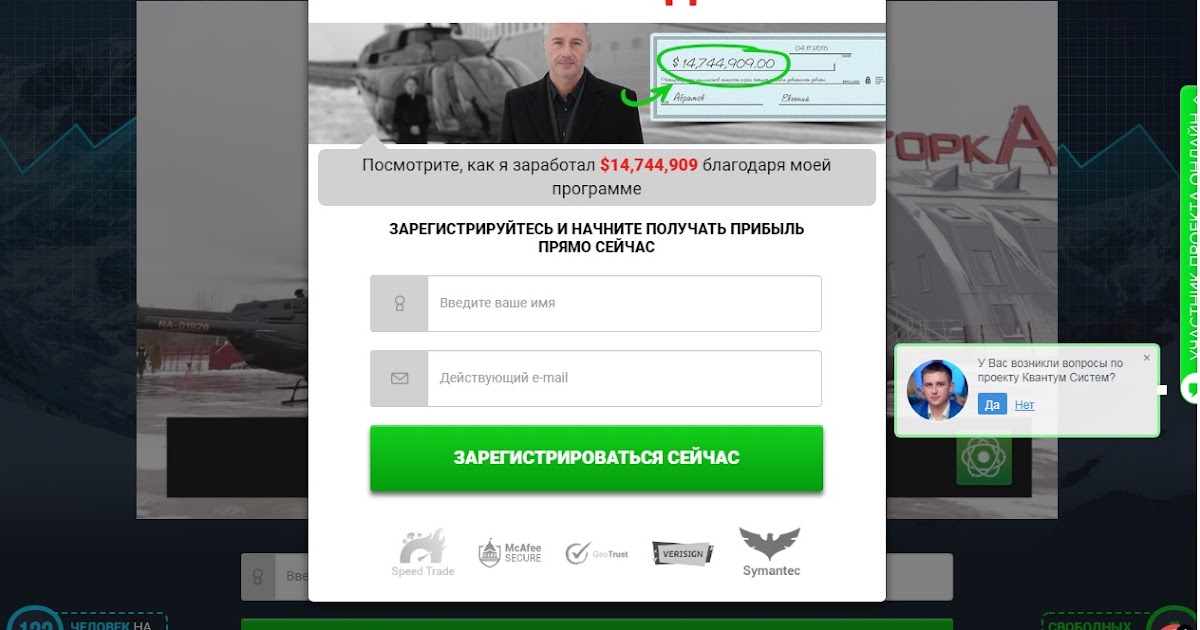
Результаты, показанные на рис. 2б, были предсказаны недавними теоретическими работами 23,24 . Связь между хаосом и запутанностью давно представляет теоретический интерес 25,26,27 . Однако эти исследования были сосредоточены на очень больших системах, близких к границе квантовой и классической физики 28,29 . Здесь мы показываем, что результаты сохраняются глубоко в квантовом пределе. Интересно отметить, что хаос и запутанность являются исключительными для своих соответствующих классических и квантовых областей, и любая связь удивительна. Соответствие тем более неожиданно, что наша система так далека от классического предела 6,30 .
На рис. 2b энтропия запутанности в синих областях приближается к 0,8, что близко к максимально достижимому значению 1,0 для одного кубита. Значение 0,8 очень близко к значению, которое можно было бы получить путем равномерного усреднения по всем состояниям, 0,73 (ссылка 31). В уравнении (2) гамильтониан зависит от времени, и в результате энергия не сохраняется.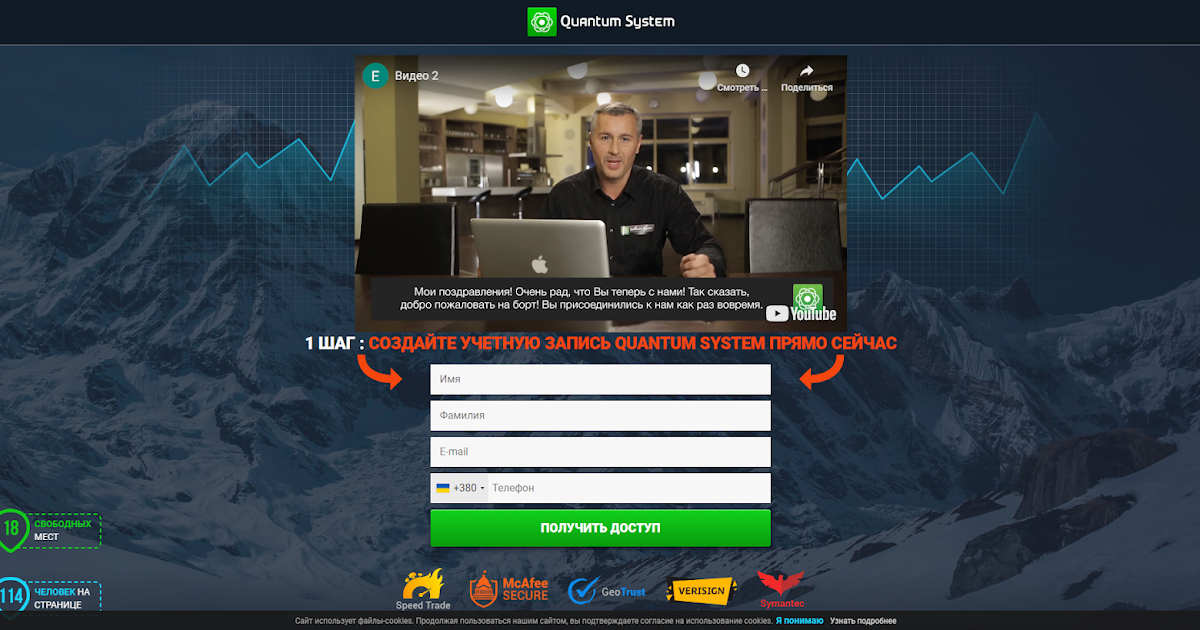
Следовательно, статистическая механика будет предсказывать значения наблюдаемых, используя ансамбль с максимальной энтропией или, что то же самое, ансамбль с бесконечной температурой. Наблюдаемая матрица плотности, приближающаяся к максимальной энтропии, предполагает, что даже небольшие квантовые системы, подвергающиеся унитарной динамике, могут казаться термальными 3,32,33 .
В дополнительной информации мы численно вычисляем эволюцию для более крупных систем и показываем, что флуктуации уменьшаются с увеличением размера системы, как и ожидалось для систем конечных размеров, приближающихся к тепловому равновесию. Кроме того, мы вычисляем поведение при больших значениях κ и показываем, что все начальные состояния получают почти максимальную энтропию, в отличие от смешанного фазового пространства, показанного на рис. 2. Это еще раз подтверждает идею о том, что то, что мы видим в эксперименте является началом термализации в небольшой квантовой системе.
Наблюдаемая энтропия одного кубита может происходить из двух источников: запутанность с другими кубитами и запутанность с окружающей средой (декогеренция).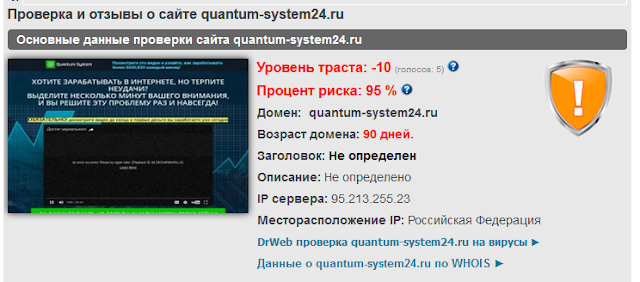
На рис. 3 мы показываем, что контраст между высокой и низкой энтропией возникает из-за запутанности кубитов, что подтверждает наше предположение о хорошей изоляции системы. Чтобы различить эти два эффекта, мы измеряем трехкубитную матрицу плотности. Используя эти измерения, мы вычисляем средние значения всех комбинаций операторов Паули. Первые девять столбцов на рис. 3 содержат операторы только для одного кубита и, таким образом, предоставляют информацию о локальных свойствах. Остальные столбцы содержат произведения двух- и трехкубитных операторов и описывают корреляции между кубитами.
Мы представляем матрицу плотности из трех кубитов для двух начальных состояний, показанных на вставке, одного с низкой энтропией (вверху) и другого с высокой энтропией (внизу). В обоих случаях начальное состояние эволюционировало за N = 10 временных шагов и κ = 0,5. Каждая полоса указывает математическое ожидание одной возможной комбинации операторов Паули на трех кубитах, соответствующий оператор показан с помощью цветных квадратов.
Увеличение многокубитных корреляций на нижней панели означает, что контраст между высокой и низкой энтропией является результатом запутанности.
Изображение полного размера
На верхней панели мы рассматриваем начальное состояние, энтропия которого увеличилась на наименьшую величину (наибольшая красная), показанная на вставке. После десяти временных шагов мы видим, что каждый кубит ориентирован вдоль оси y , на что указывают первые три пика. Кубиты, направленные в одном направлении, приводят к классическим корреляциям, на что указывают оставшиеся пики среди двух- и трехкубитных корреляций. На нижней панели мы рассматриваем начальное состояние, энтропия которого увеличилась на наибольшую величину (наибольшая синяя). В дополнение к ориентации кубитов и классическим корреляциям мы также находим много значимых пиков среди многокубитных корреляций. Эти неклассические корреляции — явные признаки запутанности кубитов. Кроме того, мы обнаруживаем, что чистота состояния трех кубитов, мера декогерентности, одинакова для обоих этих состояний, показывая, что контраст между высокой и низкой энтропией полностью является результатом запутанности между кубитами (см.
Дополнительную информацию). Этот вывод контрастирует с предыдущими исследованиями, в которых было обнаружено, что для начальных состояний с высокой энтропией система проявляла сверхчувствительность к возмущениям, таким как декогерентность окружающей среды 9.0123 17 .
Преимущество изучения статистической механики в небольшой квантовой системе состоит в том, что мы можем напрямую проверить эргодическое движение в трехкубитной динамике. Используя измерения полной многокубитной матрицы плотности, мы исследуем связь между эргодической динамикой в полной системе и производством энтропии в подсистемах. Обратите внимание, что в идеале полная система находится в чистом состоянии, энтропия которого равна нулю и остается равной нулю по мере развития системы — это резко контрастирует с подсистемами, которые со временем набирают энтропию за счет запутанности. Хотя полная система не может термироваться в смысле достижения максимальной энтропии, она может совершать эргодическое движение (усредненные по времени равны средним по пространству состояний).
В статистической механике единообразное среднее по состояниям задается микроканоническим ансамблем. На рис. 4 показано наложение усредненной по времени матрицы плотности на микроканонический ансамбль ρ mc , заданное как
Здесь ρ mc представляет собой матрицу плотности 8 на 8, которая приписывает равную вероятность всем доступным состояниям. Перекрытие этих двух распределений, приближающееся к 1,0, будет означать, что средние значения по времени эквивалентны средним значениям в пространстве состояний для всех измеряемых величин.
Рисунок 4: Эргодическая динамика. Перекрытие усредненной по времени матрицы плотности из трех кубитов с микроканоническим ансамблем (см. уравнение (6)) в зависимости от количества временных шагов N , для κ = 2,5. Мы выбираем три различных начальных состояния, показанных на вставке. Значение 1,0 указывает на то, что динамика полностью эргодическая.
Изображение полного размера
Мы выбираем три разных начальных состояния: два выбираются из областей с высокой энтропией (синий и зеленый) и одно из области с низкой энтропией (красный). Всего после трех шагов начальные состояния, в которых подсистемы имели высокую энтропию, приближаются к микроканоническому ансамблю с точностью до 94%. Численное моделирование показывает, что в идеале плато перекрытия находятся на уровне 98% — отклонения от этого идеального поведения в первую очередь связаны с декогеренцией. Мы обнаружили, что начальные состояния, в которых подсистемы имели низкую энтропию, не приближаются к микроканоническому ансамблю. Сильное перекрытие между средними значениями по времени и средними значениями в пространстве состояний демонстрирует, что динамика трех кубитов является эргодичной, и дополнительно поддерживает структуру статистической механики для понимания производства энтропии в отдельных кубитах.
Предыдущие эксперименты исследовали признаки классического хаоса в квантовых системах 17,34 .
Здесь, используя нашу способность генерировать произвольные состояния продукта, мы устанавливаем четкую сигнатуру во всем фазовом пространстве. Наши уникальные измерительные возможности позволяют нам выйти за рамки предыдущих работ, напрямую связывая наши наблюдения с запутанностью кубитов, а не с декогерентностью окружающей среды. Вместе эти инструменты позволяют продемонстрировать эргодическую динамику и показать, что сверхпроводящие кубиты можно использовать для изучения фундаментальных концепций статистической механики.
Интересно узнать об общности наших результатов, поскольку они могут обеспечить общую основу для изучения квантовой динамики. Численные результаты показывают, что эргодическое поведение нарушается только тогда, когда эволюция сильно ограничена законами сохранения; такие системы называются интегрируемыми и представляют собой модели с тонкой настройкой и, следовательно, редкие 3 . Наш выбор гамильтониана был мотивирован отсутствием сохраняющихся величин, когда сохраняется только полный спин, а не сохраняется даже энергия.
Об авторе