Письмо статистики по инн: Коды Росстата. Узнать коды статистики по ИНН или ОГРН. Получить коды статистики онлайн и распечатать Уведомление.

Содержание

Коды статистики Свердловская область получить онлайн и распечатать Уведомление.

ТЕНДЕРЫ БИЗНЕС ПЛАНЫ МАРКЕТИНГОВЫЕ ИССЛЕДОВАНИЯ

Сформировать и распечатать уведомление с кодами статистики общероссийских классификаторов:

Юридическим лицам

Индивидуальным предпринимателям

В открывшейся вкладке можно узнать коды статистики по ИНН, ОГРН или ОКПО. После нажатия кнопки Искать должны отобразиться Ваши коды статистики Росстат, а также кнопка Получить уведомление об учёте в статистическом регистре. Нажав данную кнопку загрузится автоматически сформированное Уведомление в формате Word, которое и необходимо распечатать. Сервис также позволяет скачать и распечатать расшифровку кодов ОК ТЭИ.

Адреса и контактные телефоны районных отделов территориального органа Федеральной службы государственной статистики по Свердловской области для личного обращения:

Районные отделы статистики по Свердловской области

Официальный сайт статистики по Свердловской области

Что делать, если по моему запросу ничего не найдено?

После государственной регистрации информация поступает из налоговых органов в территориальный орган Федеральной службы государственной статистики, где вносится в базы данных. Информация в базах обновляется несколько раз в месяц, как правило, это происходит после 15 и 30-31 числа каждого месяца. Поэтому, если данных о Вас в базе ещё нет, а Уведомление нужно срочно, Вы можете лично с выпиской из ЕГРЮЛ или ЕГРИП обратиться в территориальную статистику по месту Вашей регистрации. Адреса и телефоны районных отделов статистики представлены выше.

Внимание!

С 1 августа 2018 года осуществляется переход на единую базу Росстата, которая доступна по ссылке:

Получить Уведомление с кодами ОК ТЭИ

Сервис может не работать в выходные и праздничные дни. Возможно некорректное отображение в браузере Internet Explorer, работоспособность подтверждена в браузерах Chrome, Opera и Firefox. Если по каким-то причинам страница сервиса не открылась, обновите её, нажав клавишу F5, или попробуйте зайти позже.

ВЫБЕРИТЕ ВАШ СУБЪЕКТ РФ:

01 — Республика Адыгея

02 — Республика Башкортостан

03 — Республика Бурятия

04 — Республика Алтай

05 — Республика Дагестан

06 — Республика Ингушетия

07 — Кабардино-Балкарская Республика

08 — Республика Калмыкия

09 — Карачаево-Черкесская Республика

10 — Республика Карелия

11 — Республика Коми

12 — Республика Марий Эл

13 — Республика Мордовия

14 — Республика Саха (Якутия)

15 — Республ. Северная Осетия-Алания

16 — Республика Татарстан

17 — Республика Тыва

18 — Удмуртская Республика

19 — Республика Хакасия

20 — Чеченская Республика

21 — Чувашская Республика (Чувашия)

22 — Алтайский край

23 — Краснодарский край

24 — Красноярский край

25 — Приморский край

26 — Ставропольский край

27 — Хабаровский край

28 — Амурская область

29 — Архангельская область

30 — Астраханская область

31 — Белгородская область

32 — Брянская область

33 — Владимирская область

34 — Волгоградская область

35 — Вологодская область

36 — Воронежская область

37 — Ивановская область

38 — Иркутская область

39 — Калининградская область

40 — Калужская область

41 — Камчатский край

42 — Кемеровская область

43 — Кировская область

44 — Костромская область

45 — Курганская область

46 — Курская область

47 — Ленинградская область

48 — Липецкая область

49 — Магаданская область

50 — Московская область

51 — Мурманская область

52 — Нижегородская область

53 — Новгородская область

54 — Новосибирская область

55 — Омская область

56 — Оренбургская область

57 — Орловская область

58 — Пензенская область

59 — Пермский край

60 — Псковская область

61 — Ростовская область

62 — Рязанская область

63 — Самарская область

64 — Саратовская область

65 — Сахалинская область

66 — Свердловская область

67 — Смоленская область

68 — Тамбовская область

69 — Тверская область

70 — Томская область

71 — Тульская область

72 — Тюменская область

73 — Ульяновская область

74 — Челябинская область

75 — Забайкальский край (Читинская обл. )

76 — Ярославская область

77 — Город Москва

78 — Город Санкт-Петербург

79 — Еврейская автономная область

80 — Агинский Бурятский округ

83 — Ненецкий автономный округ

85 — Усть-Ордынский Бурятский округ

86 — Ханты-Мансийский АО — Югра

87 — Чукотский автономный округ

89 — Ямало-Ненецкий автономный округ

91 — Республика Крым

92 — Город Севастополь

Коды статистики Московская область получить онлайн и распечатать Уведомление.

ТЕНДЕРЫ БИЗНЕС ПЛАНЫ МАРКЕТИНГОВЫЕ ИССЛЕДОВАНИЯ

Сформировать и распечатать уведомление с кодами статистики общероссийских классификаторов:

Юридическим лицам

Индивидуальным предпринимателям

Адреса и контактные телефоны районных отделов территориального органа Федеральной службы государственной статистики по Московской области для личного обращения:

Районные отделы статистики по Московской области

Официальный сайт статистики по Московской области

Что делать, если по моему запросу ничего не найдено?

Адреса и телефоны районных отделов статистики представлены выше.

Внимание!

С 1 августа 2018 года осуществляется переход на единую базу Росстата, которая доступна по ссылке:

Получить Уведомление с кодами ОК ТЭИ

ВЫБЕРИТЕ ВАШ СУБЪЕКТ РФ:

01 — Республика Адыгея

02 — Республика Башкортостан

03 — Республика Бурятия

04 — Республика Алтай

05 — Республика Дагестан

06 — Республика Ингушетия

07 — Кабардино-Балкарская Республика

08 — Республика Калмыкия

09 — Карачаево-Черкесская Республика

10 — Республика Карелия

11 — Республика Коми

12 — Республика Марий Эл

13 — Республика Мордовия

14 — Республика Саха (Якутия)

15 — Республ. Северная Осетия-Алания

16 — Республика Татарстан

17 — Республика Тыва

18 — Удмуртская Республика

19 — Республика Хакасия

20 — Чеченская Республика

21 — Чувашская Республика (Чувашия)

22 — Алтайский край

23 — Краснодарский край

24 — Красноярский край

25 — Приморский край

26 — Ставропольский край

27 — Хабаровский край

28 — Амурская область

29 — Архангельская область

30 — Астраханская область

31 — Белгородская область

32 — Брянская область

33 — Владимирская область

34 — Волгоградская область

35 — Вологодская область

36 — Воронежская область

37 — Ивановская область

38 — Иркутская область

39 — Калининградская область

40 — Калужская область

41 — Камчатский край

42 — Кемеровская область

43 — Кировская область

44 — Костромская область

45 — Курганская область

46 — Курская область

47 — Ленинградская область

48 — Липецкая область

49 — Магаданская область

50 — Московская область

51 — Мурманская область

52 — Нижегородская область

53 — Новгородская область

54 — Новосибирская область

55 — Омская область

56 — Оренбургская область

57 — Орловская область

58 — Пензенская область

59 — Пермский край

60 — Псковская область

61 — Ростовская область

62 — Рязанская область

63 — Самарская область

64 — Саратовская область

65 — Сахалинская область

66 — Свердловская область

67 — Смоленская область

68 — Тамбовская область

69 — Тверская область

70 — Томская область

71 — Тульская область

72 — Тюменская область

73 — Ульяновская область

74 — Челябинская область

75 — Забайкальский край (Читинская обл. )

76 — Ярославская область

77 — Город Москва

78 — Город Санкт-Петербург

79 — Еврейская автономная область

80 — Агинский Бурятский округ

83 — Ненецкий автономный округ

85 — Усть-Ордынский Бурятский округ

86 — Ханты-Мансийский АО — Югра

87 — Чукотский автономный округ

89 — Ямало-Ненецкий автономный округ

91 — Республика Крым

92 — Город Севастополь

Статистика испытаний: определение, формулы и примеры

В этой статье

Что такое стандартизированная тестовая статистика?
Общая формула расчета тестовой статистики
Типы тестовой статистики с формулами
Разница между T-тестами и Z-тестами и когда их использовать
Как интерпретировать тестовую статистику

Что такое стандартизированная тестовая статистика?

Тестовая статистика — это стандартизированная оценка, используемая при проверке гипотез.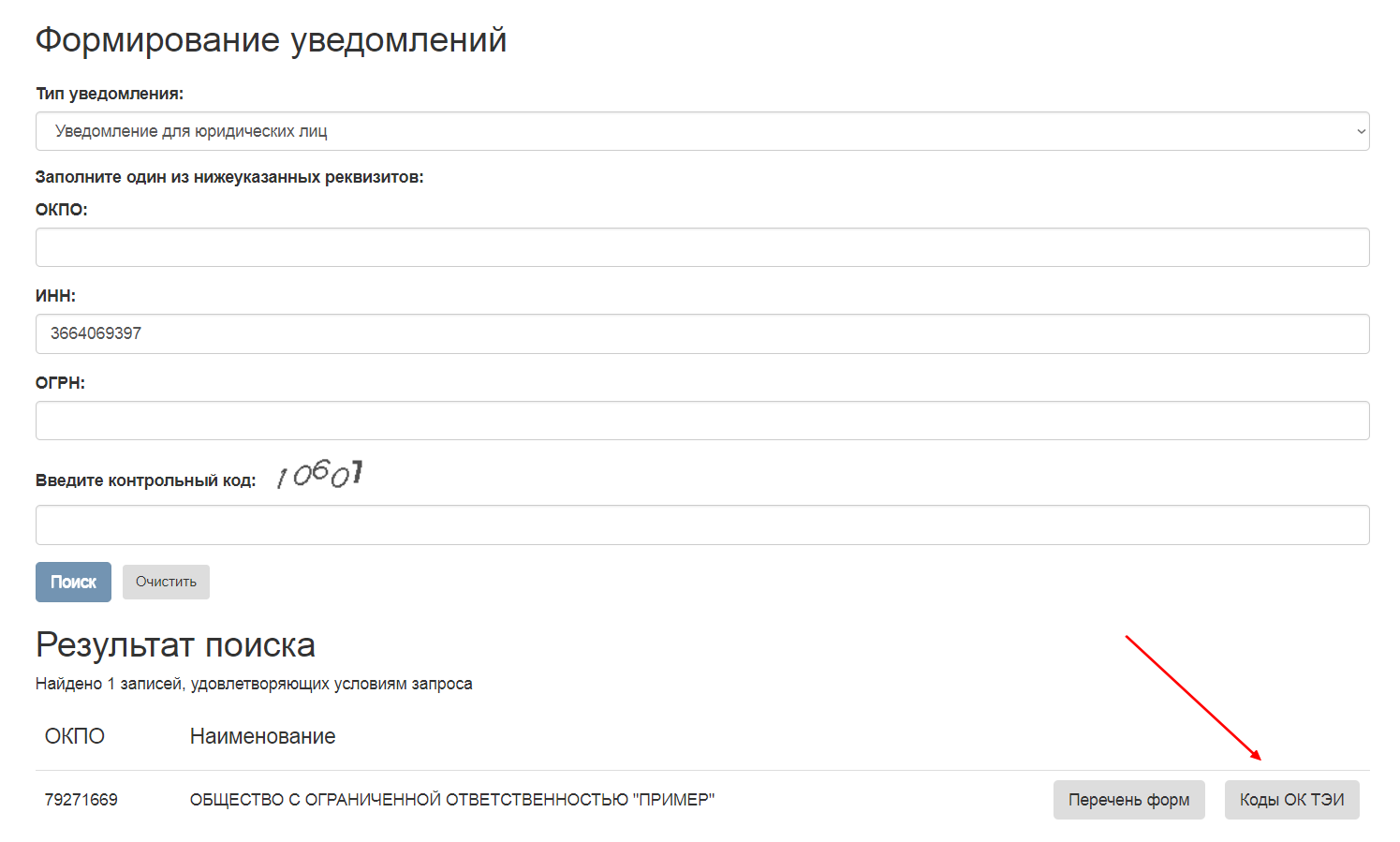 Он сообщает вам, насколько вероятны результаты, полученные из ваших выборочных данных, при условии, что нулевая гипотеза верна. Чем более маловероятными будут ваши результаты при таком предположении, тем легче будет отвергнуть нулевую гипотезу в пользу альтернативной гипотезы. Чем более вероятны ваши результаты, тем труднее отвергнуть нулевую гипотезу.

Существуют разные виды тестовой статистики, но все они работают одинаково. Тестовая статистика сопоставляет значение конкретной выборочной статистики (такой как выборочное среднее или выборочная пропорция) со значением стандартизированного распределения, такого как стандартное нормальное распределение или t-распределение. Это позволяет вам определить, насколько вероятно или маловероятно наблюдать конкретное значение полученной вами статистики.

Оланреваджу Майкл Аканде рассматривает нормальное распределение в следующем уроке:

В качестве быстрого примера предположим, что у вас есть нулевая гипотеза о том, что среднее время ожидания, чтобы занять место в вашем любимом ресторане — за столиком на двоих без предварительного бронирования на Вечер пятницы — 45 минут. Вы выбираете случайную выборку из 100 участников, которые заняли свои места в этих условиях, и спрашиваете их, какое у них было время ожидания. Вы обнаружите, что среднее время ожидания вашего образца составляет 55 минут (xˉ \bar{x}xˉ = 55 минут). Тестовая статистика преобразует эту выборочную статистику xˉ \bar{x}xˉ в стандартизированное число, которое поможет вам ответить на этот вопрос:

«Предполагая, что моя нулевая гипотеза верна — предположим, что среднее время ожидания в ресторане на самом деле составляет 45 минут, — какова вероятность того, что я нашел среднее время ожидания 55 минут для моей случайно выбранной выборки?»

Помните, чем ниже вероятность наблюдения вашей выборочной статистики, тем с большей уверенностью вы можете отвергнуть нулевую гипотезу.

Тип тестовой статистики, которую вы используете в проверке гипотезы, зависит от нескольких факторов, в том числе:

Тип статистики, которую вы используете в тесте
Размер вашей выборки
Ваши предположения относительно распространения ваших данных
Предположения, которые вы можете сделать о распределении статистики, используемой в тесте

Общая формула расчета тестовой статистики

Формула расчета тестовой статистики имеет следующий общий вид:

Статистика теста=Статистика-ПараметрСтандартное отклонение статистики\text{Статистика теста} = \frac{\text{Статистика} — \text{Параметр}}{\text{Стандартное отклонение статистики}} Статистика теста = стандартное отклонение статистического параметра StatisticStatistic

Помните, что статистика – это мера, вычисляемая на основе одной выборки или множества выборок. .
Параметр — это мера, вычисляемая по одной или нескольким совокупностям. Примеры включают среднее значение совокупности μ\muμ, разницу между двумя средними значениями совокупности μ1−μ2\mu_{1}-\mu_{2}μ1−μ2 или долю населения ppp.
В знаменателе уравнения у вас есть стандартное отклонение — или приближенное стандартное отклонение — статистики, используемой в числителе. Если вы используете выборочное среднее xˉ\bar{x}xˉ, в числителе вы должны использовать стандартное отклонение xˉ\bar{x}xˉ или его приближение в знаменателе.

Типы тестовой статистики с формулами

Тестовая статистика, с которой вы, скорее всего, столкнетесь на вводном уроке статистики:

Статистика Z-критерия для одной выборки означает
Статистика Z-теста для пропорций населения
Статистика t-теста для одной выборки означает
Статистика t-критерия для двух выборок означает

Z-критерий выборочного среднего

Мы используем статистику Z-теста (или Z-статистику) для выборочного среднего в проверках гипотез, включающих выборочное среднее xˉ\bar{x}xˉ, рассчитанное для одной выборки.

Вы используете эту тестовую статистику, когда:

Размер вашей выборки больше или равен 30 (n≥\geq≥30)
Предполагается, что выборочное распределение среднего значения выборки является нормальным
Стандартное отклонение параметра генеральной совокупности σ\sigmaσ известно.

Формула для этого типа статистики Z-теста:

Z=xˉ−μ0σnZ =\frac{\bar{x}-\mu_{0}}{\frac{\sigma}{\sqrt{n}}}Z=n

σxˉ−μ0

ZZZ является символом статистики Z-теста
xˉ\bar{x}xˉ — выборочное среднее
μ0\mu_{0}μ0 — предполагаемое значение среднего значения генеральной совокупности согласно нулевой гипотезе
σ\sigmaσ — стандартное отклонение совокупности
nnn — размер выборки
σn\frac{\sigma}{\sqrt{n}}nσ — стандартная ошибка xˉ\bar{x}xˉ. Стандартная ошибка — это просто стандартное отклонение выборочного распределения выборочного среднего.

Вы можете заметить, что статистика Z-теста — это просто z-оценка для определенного значения нормально распределенной статистики. Существует множество вариаций статистики Z-теста. Мы можем использовать их в тестах гипотез, где выборочная статистика, используемая в тесте, имеет приблизительно нормальное распределение. Одним из таких вариантов статистики Z-теста является Z-тест пропорций. 9 – доля выборки

p0p_{0}p0 – гипотетическое значение доли населения в соответствии с нулевой гипотезой

nnn — размер выборки

Если размер вашей выборки меньше 30 (n

Т-критерий для среднего значения одной выборки)

Мы используем статистику t-критерия (или t-статистику) для выборочного среднего в проверках гипотез, включающих выборочное среднее, рассчитанное для одной выборки, взятой из совокупности. В отличие от Z-теста для среднего значения одной выборки, вы используете t-критерий, когда:

Размер вашей выборки меньше 30 (n
Распределение выборочной статистики не аппроксимируется нормальным распределением
Стандартное отклонение параметра совокупности σ\sigmaσ неизвестно.

Статистика t-теста сопоставляет вашу статистику с t-распределением, в отличие от нормального распределения с Z-тестом. Стьюдентное распределение похоже на стандартное нормальное распределение, но имеет более толстые хвосты и изменяется в зависимости от размера выборки nnn. Когда nnn велико, t-распределение ближе к нормальному; и по мере того, как размер выборки становится все больше и больше, t-распределение будет сходиться к нормальному распределению. По мере того, как nnn становится меньше, t-распределение становится более плоским с более толстыми хвостами.

Формула для статистики t-критерия для выборочного среднего:

t=xˉ−μ0snt =\frac{\bar{x}-\mu_0}{\frac{s}{\sqrt{n}}}t=n

sxˉ−μ0

ttt — это символ статистики t-критерия
xˉ\bar{x}xˉ — выборочное среднее
μ0\mu_0μ0 — значение среднего значения генеральной совокупности согласно нулевой гипотезе
sss – стандартное отклонение выборки
nnn — размер выборки
sn\frac{s}{\sqrt{n}}ns является аппроксимацией стандартной ошибки xˉ\bar{x}xˉ. В t-тесте, поскольку вы не знаете значение стандартного отклонения совокупности, вам необходимо аппроксимировать стандартную ошибку xˉ\bar{x}xˉ, используя стандартное отклонение выборки sss.

Т-критерий для двух средних значений

Мы также можем использовать статистику t-критерия в тестах гипотез, где сравниваются значения двух выборочных средних (x1x_{1}x1 и x2x_{2}x2). Вы делаете это, чтобы проверить нулевую гипотезу о том, что две выборки взяты из одной и той же базовой совокупности. Если нулевая гипотеза верна, то любое различие между выборочными средними связано со случайными вариациями данных. Отклонение нулевой гипотезы предполагает, что выборки были взяты из двух разных популяций и что разница в средних выборках отражает фактические различия в характеристиках субъектов в одной популяции по сравнению с другой.

Как и критерий Стьюдента для среднего значения одной выборки, критерий Стьюдента для среднего значения двух образцов используется, когда:

Размеры вашей выборки меньше 30 (n
Распределение статистики выборки не аппроксимируется нормальным распределением
Стандартное отклонение параметра совокупности σ\sigmaσ неизвестно.

Формула для статистики t-критерия для двух выборочных средних‌: 92}{n_2}}}}t=n1s12+n2s22

(x1ˉ−x2ˉ)(µ1µ2)

ttt — символ для статистики t-теста
x1ˉ\bar{x_1}x1ˉ — выборочное среднее для выборки 1
x2ˉ\bar{x_2}x2ˉ — выборочное среднее для выборки 2
μ1\mu_1μ1 — среднее значение совокупности, из которой была взята выборка 1
μ2\mu_2μ2 — среднее значение генеральной совокупности, из которой была взята выборка 2 92s22 — дисперсия выборки 2
n1n_{1}n1 – размер выборки для выборки 1
n2n_{2}n2 – размер выборки для выборки 2.

Разница между T-тестами и Z-тестами и когда их использовать

T-тесты обычно используются вместо Z-тестов, когда выполняется одно или несколько из следующих условий: Размер выборки меньше 30 (n\sigma неизвестно

Если вам известно стандартное отклонение генеральной совокупности σ\sigmaσ и вы уверены, что статистика, используемая при проверке вашей гипотезы, имеет нормальное распределение, то вы можете использовать Z-тест.

Как и в случае со всей тестовой статистикой, вы должны использовать Z-критерий или t-критерий только в том случае, если ваши данные взяты из произвольной и независимой выборки.

Как интерпретировать статистику теста

Мы используем тестовую статистику вместе с критическими значениями, p-значениями и уровнями значимости, чтобы определить, следует ли отвергать нулевую гипотезу.

Критическое значение — это значение тестовой статистики, которое отмечает точку отсечки. Если тестовая статистика более экстремальна, чем критическое значение — больше критического значения в правом хвосте распределения или меньше критического значения в левом хвосте распределения — нулевая гипотеза отклоняется.

Критические значения определяются уровнем значимости (или альфа-уровнем) проверки гипотезы. Уровень значимости, который вы используете, зависит от вас, но чаще всего используется уровень значимости 0,05 (α\alphaα=0,05).

Уровень значимости 0,05 означает, что если вероятность наблюдения выборочной статистики, по крайней мере столь же экстремальной, как та, которую вы наблюдали, меньше 0,05 (или 5%), вы должны отвергнуть свою нулевую гипотезу. В одностороннем тесте гипотезы, использующем статистику Z-теста, уровень значимости 0,05 связан с критическим значением 1,645 при проведении теста в правом хвосте и значением -1,645 при проведении теста в правом хвосте. левый хвост.

Значение p – это вероятность, связанная со значением статистики вашего теста. Допустим, вы вычисляете статистику Z-теста, которая соответствует стандартному нормальному распределению. Вы обнаружите, что тестовая статистика равна 1,75. Для этого ‌значения статистики Z-теста связанное значение p равно 0,04 или 4% — вы можете найти значения p с помощью таблиц или статистического программного обеспечения.

Значение p, равное 0,04, означает, что вероятность наблюдения выборочной статистики, по крайней мере, такой же экстремальной, как та, которую вы нашли на основе данных выборки, составляет 4%. Если вы выберете уровень значимости 0,05 для своего теста, мы отклоним нулевую гипотезу, поскольку значение p 0,04 меньше, чем уровень значимости 0,05.

Легко перепутать статистику испытаний, критические значения, уровни значимости и p-значения. Помните, что все это разные меры, используемые для определения того, отвергать или не отвергать нулевую гипотезу.

Критические значения и уровни значимости обеспечивают пороговые значения для вашего теста. Разница между критическим значением и уровнем значимости заключается в том, что критическое значение — это точка на распределении, а уровень значимости — это вероятность, представленная областью под распределением.

Вы можете сравнить статистику теста и p-значение с критическим значением и уровнем значимости.

Если тестовая статистика более экстремальна, чем критическое значение, вы отвергаете нулевую гипотезу.
Если p-значение меньше уровня значимости, вы отвергаете нулевую гипотезу.
Если тестовая статистика менее экстремальна, чем критическое значение, вы не можете отвергнуть нулевую гипотезу.
Если p-значение больше уровня значимости, вы отвергаете нулевую гипотезу.

Ознакомьтесь с отмеченными наградами курсами For-Credit от Outlier

Outlier (от соучредителя MasterClass) собрал лучших в мире преподавателей, дизайнеров игр и кинематографистов для создания будущего онлайн-колледжа.

Ознакомьтесь с этими родственными курсами:

Статистика бейсбола — BR Bullpen

Статистика очень важна для бейсбола , возможно, больше, чем для любого другого вида спорта. Поскольку игра в бейсбол имеет очень структурированный ход, игра поддается легкому ведению записей и статистики. Это позволяет относительно легко сравнивать результаты игроков на поле и, следовательно, придает бейсбольной статистике большее значение, чем в большинстве других видов спорта.

Содержание

1 Развитие статистики
2 Использование статистики
3 Часто используемые статистические данные
- 3.1 Статистика ударов
- 3.2 Базовая статистика
- 3. 3 Статистика подачи
- 3.4 Статистика игры
- 3.5 Общая статистика
4 Дополнительная литература
5 Связанные сайты

Развитие статистики[править]

Практика учета достижений игроков была начата в 19 веке Генри Чедвиком. Чедвик разработал предшественников современной статистики, такой как средний результат, количество забитых пробежек и разрешенных пробежек, основываясь на своем опыте игры в крикет.

Традиционно статистическим миром бейсбола управляли такие статистические данные, как средний показатель отбивающих (количество попаданий, деленное на количество отбитых мячей) и средний заработанный пробег (приблизительно количество пробежок, пропущенных питчером за девять иннингов). Однако недавнее появление саберметрики вызвало натиск новой статистики. Эти статистические данные предназначены для лучшего измерения производительности игрока и его вклада в свою команду из года в год.

Всеобъемлющая историческая бейсбольная статистика была труднодоступной для среднего болельщика до 19 лет. 51, когда исследователь Хай Туркин опубликовал «Полную энциклопедию бейсбола». В 1969 году MacMillan Publishing напечатала свою первую энциклопедию бейсбола, впервые используя компьютер для сбора статистики. «Биг-Мак» стал стандартным отсылкой к бейсболу до 1988 года, когда Warner Books выпустила Total Baseball с использованием еще более сложной технологии. Интересно, что эта работа привела к обнаружению нескольких игроков, которым не было места в официальных книгах рекордов. Некоторые из этих «призрачных игроков в мяч», такие как Лу Проктор, были исключены из книг рекордов.

Использование статистики[править]

Генеральные менеджеры и бейсбольные скауты изучают статистику игроков, чтобы принимать решения о способностях игроков. Менеджеры, ловцы и питчеры изучают статистику отбивающих в командах соперников, чтобы выяснить, как лучше всего подать им и расположить игроков на поле. Менеджеры и отбивающие изучают питчеров соперников, чтобы выяснить, как лучше всего бить по ним. Менеджеры часто основывают свои кадровые решения во время игры на статистике, например, выбирая, кого поставить в состав или какого запасного питчера ввести.

На протяжении большей части современного бейсбола традиционно используются несколько основных статистических данных. Среднее количество ударов, ИКР и хоум-раны — это наиболее часто упоминаемые статистические данные об ударах. По сей день игрока, который лидирует в лиге по этим трем показателям, называют победителем «Тройной короны». Для питчеров наиболее часто цитируемой традиционной статистикой являются победы, ERA и ауты. Питчер, которому удается возглавить лигу по этой статистике, также упоминается как победитель «Тройной короны».

Некоторые саберметрические статистические данные вошли в основной бейсбольный мир. Среди статистических данных, которые измеряют общую производительность отбивающего, показатель «На базе плюс пробивка» (OPS) является одним из самых простых для расчета. Он добавляет базовый процент нападающего (количество раз, когда он достиг базы — любым способом — деленное на общее количество появлений тарелок) к его или ее проценту пробивных (общее количество баз, деленное на летучих мышей).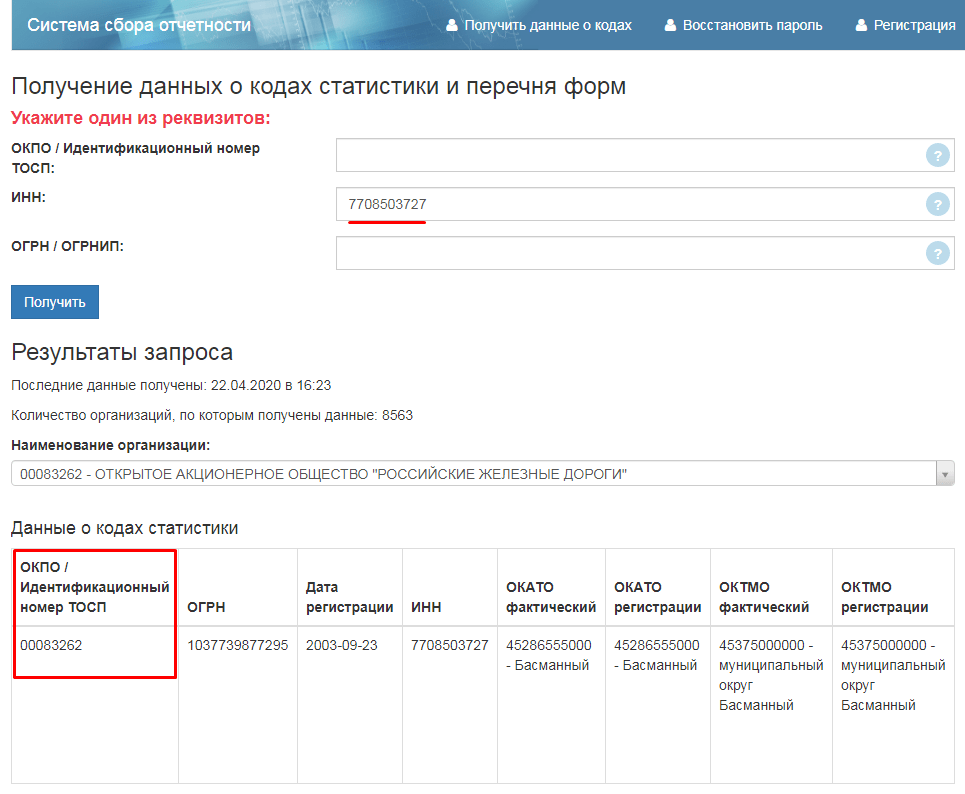 Некоторые утверждают, что формула OPS ошибочна и что больший вес должен быть смещен в сторону OBP (в базовом процентном соотношении).

OPS также полезен при определении уровня успеха питчера. «Противник на базе плюс удар» (OOPS) становится популярным способом оценки фактической игры питчера. При анализе статистики питчера следует учитывать некоторые полезные категории, в том числе K/9IP (страйкауты за девять иннингов), K/BB (страйкауты за прогулку) и HR/9. WHIP (ходьба плюс количество попаданий за подачу) и OOPS (противник на базе плюс пробивка).

Однако с 2001 года больше внимания уделяется независимой от защиты статистике подачи. Эти статистические данные, такие как ERA, независимая от защиты (dERA), пытаются оценить питчера в соответствии с теми событиями, которые регулируются исключительно игрой питчера, независимо от силы защитников позади него или нее.

Также важна вся вышеперечисленная статистика в определенных игровых ситуациях. Например, способность определенного нападающего бить питчеров-левшей может побудить менеджера дать ему или ей больше шансов встретиться с левшами. У других нападающих может быть история успеха против данного питчера (или наоборот), и менеджер может использовать эту информацию для организации благоприятного матча.

Обычно используемые статистические данные Здесь объясняются часто используемые статистические данные с их сокращениями. Приведенные ниже пояснения предназначены для быстрого ознакомления и не полностью или полностью определяют статистику; для строгого определения см. соответствующую статью для каждой статистики.

Статистика отбивания

2B — Двойные удары, при которых отбивающий благополучно достиг второй базы без участия ошибки поля.

3B — Тройной — удары, при которых отбивающий благополучно достиг третьей базы без участия ошибки поля.

AB — В игре с битой — Выступления с отбиванием мяча, не включая базы на мяче, удары подачей, жертвы, помехи или препятствия

AB/HR У летучих мышей на хоумран — количество битов, разделенное на количество хоумранов

BA — Среднее число ударов (также сокращенно AVG ) — количество попаданий, деленное на at

BB — База на мячах (также называемая «прогулкой») — время приема четырех мячей и перехода на первую базу

BB/K — отношение количества ходов к страйкауту — количество баз на шарах, деленное на количество аутов

XBH — Дополнительные базовые хиты — удвоение плюс тройка плюс хоумран

FC — Выбор полевого игрока — время достижения базы, когда полевой игрок решил попытаться обыграть другого бегуна

AO/GO — Коэффициент флайбола при наземном мяче — количество аутов при наземном мяче, деленное на количество аутов при флайболе

GDP или GiDP — Приземлено в двойную игру — количество ударов по наземным мячам, которые стали двойными играми

GS — Большой шлем — хоумран с загруженными базами, в результате чего засчитано четыре рана и четыре RBI зачислены отбивающему.

H — Попадания — количество попаданий на базу из-за отбитого мяча без ошибок со стороны защиты

HBP — Удар по полю — количество касаний подачей и получение первой базы в результате

HR — хоум-раны — удары, при которых отбивающий успешно коснулся всех четырех баз без участия ошибки поля.

IBB — Преднамеренная база на мячах База на мячах (см. BB выше), преднамеренно брошенных питчером. Также известен как IW (преднамеренная прогулка).

K — Забастовка — количество раз, когда третий удар был взят или замахнулся и промахнулся, или был фол с бантом

LOB — Оставлено на базе — количество бегунов, которые не выбыли из игры и не получили очков в конце иннинга.

OBP — В процентном отношении к базе — время достижения базы (H + BB + HBP), деленное на количество летучих мышей плюс ходьба плюс попадание по полю плюс жертвенные мухи (AB + BB + HBP + SF).

OPS — На базе плюс пробивка — процент на базе плюс пробивка в среднем

PA — Внешний вид пластины — количество завершенных матчей

RC — Создано ранов — статистика, которая пытается измерить, сколько ранов игрок внес в свою команду

RBI — Run batted in — количество бегунов, которые набрали очки из-за действий отбивающего, за исключением случаев, когда отбивающий приземлился в двойную игру или достиг по ошибке

SF — Sacrifice fly — количество аутов, которые позволяют другому бегуну продвигаться по базовым дорожкам или набрать

очков.

SH — Жертвенный удар — количество жертвоприношений, которое позволяет другому бегуну продвигаться по базовым путям или набрать

очков.

SLG — Средняя пробивка — общее количество баз, деленное на летучих мышей

TA — Общее среднее значение — общее количество баз, плюс прогулки, плюс кражи, деленное на появление на тарелке плюс пойманные на краже

ТБ — Всего баз — по одной на каждую одиночную, две на каждую двойную, три на каждую тройную и четыре на каждую хоумран

TOB — Время на базе — время достижения базы в результате попаданий, прогулок и ударов по полям

Статистика бейсраннинга

SB — Украденная база — количество баз, продвинутых за исключением отбитых мячей, прогулок или ударов по полю

R — Количество забитых ранов — количество легально и безопасно достигших домашней базы

Статистика подачи0008

BB — База на мячах (также называемая «прогулкой») — время подачи четырех мячей, позволяющее бегуну-бэттеру перейти на первую базу

BB/9 — База числа мячей, умноженная на девять, разделенная на количество сыгранных иннингов (база на количество мячей на 9 сыгранных иннингов)

BF — Всего столкновений с отбивающими — общее количество появлений на тарелках соперника

BK — Блокировка — количество раз, когда питчер совершает незаконную подачу или другое незаконное действие при контакте с накладкой для подачи, что позволяет бейсраннерам продвигаться вперед

BS — Пропущенное сохранение — количество входов в игру в ситуации сохранения и начисления счета за пробег, который связывает игру.

CERA — Component ERA — оценка ERA питчера на основе отдельных компонентов его статистической линии (K, H, 2B, 3B, HR, BB, HBP)

CG — Полная игра — количество игр, в которых игрок был единственным питчером в своей команде

DICE — Defence-Independent Component ERA — оценка ERA питчера на основе независимых от защиты компонентов его статистической линии (K, HR, BB, HBP)

ER — Earned run — количество прогонов, которые не произошли в результате ошибок или пропущенных мячей

ERA — среднее количество заработанных пробежек — количество заработанных пробежек в игре (обычно девять), деленное на число подач, проведенных

G — Игры с подачей (также известные как «Выступления») — количество раз, когда питчер подавал за сезон

GF — Игры завершены — количество игр, в которых игрок был последним питчером своей команды

G/F — Соотношение наземных мячей и летающих мячей — допустимые наземные мячи делятся на разрешенные летающие мячи

GS — Старты — количество игр, в которых игрок был первым питчером своей команды

H/9 — Количество попаданий за девять иннингов — разрешенное количество попаданий, умноженное на девять, разделенное на количество сыгранных подач (также известное как H/9IP — количество попаданий, разрешенных за 9 подач)

H — Разрешено попаданий — разрешено общее количество попаданий

HB — Hit batsman — количество попаданий в бэтсмена с подачей, что позволяет бегуну перейти на первую базу

HLD (или H) — Hold — количество геймов, вступивших в сейв-ситуацию, оставшихся в сэйв-ситуации, зафиксировавших хотя бы один аут и не потерявших лидерство

HR — Разрешены хоумраны — разрешено общее количество хоумранов

IBB — Умышленная база на мячах разрешена

IR — Унаследованные бегуны — количество бегунов на базе, когда питчер входит в игру

IRA — Разрешены унаследованные пробеги — количество унаследованных бегунов, которым разрешено набирать очки

IP — Иннингс подача — количество аутов, записанных во время подачи, разделенное на три

IP/GS — Среднее количество подач за игру

K — Strikeout — количество отбивающих, получивших страйк три

K/9 — количество аутов за девять иннингов — количество аутов, умноженное на девять, разделенное на количество сыгранных иннингов (количество аутов на 9 сыгранных иннингов)

K/BB — Отношение количества страйкаутов к прохождению — количество страйкаутов, деленное на количество баз на шарах

L — Проигрыш — количество игр, в которых питчер подавал, в то время как команда соперника лидировала, никогда не теряла лидерство и продолжала выигрывать

OBA — Среднее количество ударов соперников — разрешенные удары, разделенные на количество битых, с которыми столкнулись

PIT — Брошенные броски (количество бросков)

RA — Среднее количество пробежек — количество разрешенных пробежек, умноженное на девять, разделенное на количество подач

RAA — Runs Against Average — саберметрическая статистика для прогнозирования процента выигрышей.

SO — Shutout — количество полных игр без разрешенных пробежек

SV — Сейв — количество игр, в которых питчер вступает в игру под руководством команды питчера, заканчивает игру, не уступив лидерство, не является победившим питчером, и либо (a) преимущество составляло три рана или меньше, когда питчер вошел игра; (b) потенциальный ничейный пробег был на базе, на летучей мыши или на палубе; или (c) питчер провел три или более иннинга

W — Win — количество игр, в которых питчер подавал, пока его команда лидировала и продолжала побеждать (также связано: процент побед )

WP — Дикие поля — взимается, когда поле слишком высокое, низкое или слишком широкое от домашней площадки, чтобы кэтчер мог выйти на поле, что позволяет одному или нескольким бегунам продвинуться вперед или набрать очки

Статистика игры на поле Голевые передачи — количество аутов, зарегистрированных в игре, когда полевой игрок коснулся мяча, за исключением случаев, когда такое касание является аутом

DP — Двойная игра — по одной за каждую двойную игру, во время которой полевой игрок зафиксировал аут или результативную передачу.

E — Ошибки — количество раз, когда полевой игрок не смог сыграть, как он должен был сделать с общими усилиями, и в результате нападение выиграло

FP — процент выставления на поле — общее количество игр (шансы минус ошибки), деленное на общее количество моментов

ИНН — Иннингс — количество иннингов, которые игрок находится на одной определенной позиции

PB — Пропущенный мяч — начисляется кэтчеру, когда мяч вброшен и один или несколько бегунов продвигаются вперед

PO — Putout — количество раз, когда полевой игрок помечает, форсирует или апеллирует к бегуну, и в результате он выбывает из игры

RF — Коэффициент дальности — ([аутауты + передачи]*9)/сыгранные иннинги. Используется для определения количества поля, которое игрок может покрыть

SB — Украденные базы — количество раз, когда бегун продвигался по полю, не будучи выброшенным кэтчером

TC — Всего шансов — голевые передачи плюс ауты плюс ошибки

TP — Тройная игра — по одному за каждую тройную игру, во время которой полевой игрок зафиксировал путаут или результативную передачу

Общая статистика[править]

G — Сыгранные игры — количество игр, в которых игрок сыграл полностью или частично Бейсбол, статистика и роль случая в игре , Copernicus Books, New York, NY, 2001. ISBN 978-0387988160
Джим Альберт: Преподавание статистики с использованием бейсбола , 2-е издание, Mathematical Association of America Press, Провиденс, Род-Айленд, 2017. ISBN 978-1-93951-216-1
Габриэль Б. Коста, Майкл Р. Хубер и Джон Т. Саккоман: Понимание Sabermetrics: введение в науку о бейсбольной статистике , McFarland, Jefferson, NC, 2008.
Уильям Дарби: Деконструкция Высшей бейсбольной лиги, 1991-2004: Как статистика освещает индивидуальные и командные выступления , McFarland, Jefferson, NC, 2006.
Стив Гарднер: «Расширенная статистика MLB: ваш путеводитель по WAR, BABIP, FIP и многому другому», USA Today , 17 июля 2019 г. [1]
Гэри Джиллетт и Лайл Спатц: «Не высеченные в камне … Непреходящие рекорды бейсбола и эра SABR», The Baseball Research Journal , SABR, том 40, номер 2 (осень 2011 г.), стр. 7-11.
Гленн Гуццо: Новая игра с мячом: понимание бейсбольной статистики для случайного фаната , ACTA Sports, Skokie, IL, 2007.
Билл Джеймс: «Статистика», Джеффри С. Уорд и Кен Бернс: Бейсбол: иллюстрированная история , Альфред А. Кнопф, Нью-Йорк, штат Нью-Йорк, 1994, стр. 101-103.
Кейт Лоу: Умный бейсбол: история старых статистических данных, которые разрушают игру, новых, которые ее управляют, и правильный способ думать о бейсболе , HarperCollins, Нью-Йорк, штат Нью-Йорк, 2017. ISBN 978- 00624
Филип Ли: Black Stats Matter: включение номеров негритянской лиги в отчеты Высшей лиги , McFarland, Jefferson, NC, 2022. ISBN 978-1-4766-8834-3
Боб Моррис: Base Ball: простая статистика для простой игры , Outskirts Press, Денвер, Колорадо, 2021. ISBN 978-1977236555
Кевин Риви и Райан Спэдер: Невероятная статистика бейсбола: самые крутые и странные статистические данные и факты в истории бейсбола , Sports Publishing LLC, Нью-Йорк, штат Нью-Йорк, 2016. ISBN 978-1-6132-1894-5
Алан Шварц: Игра чисел: увлечение бейсболом на протяжении всей жизни со статистикой , St.

Письмо статистики по инн: Коды Росстата. Узнать коды статистики по ИНН или ОГРН. Получить коды статистики онлайн и распечатать Уведомление.