Порядок расчетов показателей коэффициентов: МЕТОДИКА РАСЧЕТА ПОКАЗАТЕЛЕЙ ФИНАНСОВОГО СОСТОЯНИЯ СЕЛЬСКОХОЗЯЙСТВЕННЫХ ТОВАРОПРОИЗВОДИТЕЛЕЙ \ КонсультантПлюс

Порядок расчетов показателей коэффициентов: МЕТОДИКА РАСЧЕТА ПОКАЗАТЕЛЕЙ ФИНАНСОВОГО СОСТОЯНИЯ СЕЛЬСКОХОЗЯЙСТВЕННЫХ ТОВАРОПРОИЗВОДИТЕЛЕЙ \ КонсультантПлюс

РАСЧЕТ ПОКАЗАТЕЛЕЙ ФИНАНСОВОГО СОСТОЯНИЯ СЕЛЬСКОХОЗЯЙСТВЕННЫХ ТОВАРОПРОИЗВОДИТЕЛЕЙ \ КонсультантПлюс

Утвержден

Протоколом

заседания межведомственной

федеральной комиссии

по финансовому оздоровлению

сельскохозяйственных

товаропроизводителей

от 25 февраля 2003 г. N 4

Порядок расчета показателей финансового состояния сельскохозяйственных товаропроизводителей для отнесения их к группам по финансовой устойчивости на основе балльной оценки показателей разработан в соответствии с Методикой расчета показателей финансового состояния сельскохозяйственных товаропроизводителей, утвержденной 30 января 2003 года Правительством Российской Федерации.

КонсультантПлюс: примечание.

Приказ Минфина РФ от 22.07.2003 N 67н, утвердивший форму бухгалтерского баланса (форма N 1), утратил силу начиная с годовой бухгалтерской отчетности за 2011 год в связи с изданием Приказа Минфина РФ от 22.09.2010 N 108н. Приказом Минфина РФ от 02.07.2010 N 66н утверждена новая форма бухгалтерского баланса.

1. Для расчета показателей финансового состояния сельскохозяйственных товаропроизводителей используются данные бухгалтерского баланса (форма N 1 по ОКУД) годовой бухгалтерской отчетности.

2. Финансовое состояние сельскохозяйственных товаропроизводителей определяется с помощью следующих показателей.

2.1. Коэффициент абсолютной ликвидности (К1) рассчитывается как отношение ликвидных активов к сумме краткосрочных обязательств, кредиторской задолженности и прочим краткосрочным обязательствам:

К1 = (стр. 250 + стр. 260) /

/ (стр. 610 + стр. 620 + стр. 660).

Данный коэффициент показывает, какая часть текущих обязательств может быть погашена средствами, имеющими абсолютную ликвидность (т.е. деньгами, ценными бумагами со сроком погашения до одного года).

2.2. Коэффициент «критической оценки» (К2) рассчитывается как отношение суммы ликвидных активов и быстро реализуемых активов (дебиторская задолженность, платежи по которой ожидаются в течение 12 месяцев) к сумме краткосрочных обязательств, кредиторской задолженности и прочим краткосрочным обязательствам:

К2 = (стр. 240 + стр. 250 + стр. 260) /

/ (стр. 610 + стр. 620 + стр. 660).

Данный коэффициент показывает, какая часть краткосрочных обязательств предприятия может быть немедленно погашена за счет денежных средств на различных счетах, в краткосрочных ценных бумагах, а также поступлений по расчетам (дебиторской задолженности).

2.3. Коэффициент текущей ликвидности (К3) рассчитывается как отношение оборотных средств к сумме краткосрочных обязательств, кредиторской задолженности и прочим краткосрочным обязательствам:

К3 = (стр. 210 + стр. 230 + стр. 240 + стр. 250 +

+ стр. 260 + стр. 270) / (стр. 610 + стр. 620 + стр. 660).

Данный коэффициент показывает, какую часть текущих обязательств можно погасить, мобилизовав все оборотные средства.

2.4. Коэффициент обеспеченности собственными средствами (К4) рассчитывается как отношение разности собственных капиталов и резервов организации и внеоборотных активов к оборотным активам:

К4 = (стр. 490 — стр. 190) / стр. 290.

Данный коэффициент показывает, какая часть оборотных активов финансируется за счет собственных оборотных источников.

2.5. Коэффициент финансовой независимости (К5) рассчитывается как отношение собственных капиталов и резервов организации к итогу баланса:

К5 = стр. 490 / стр. 700.

Данный коэффициент показывает удельный вес собственных средств в общей сумме пассивов (активов).

2.6. Коэффициент финансовой независимости в части формирования запасов и затрат (К6) рассчитывается как отношение собственных капиталов и резервов организации к сумме запасов и налога на добавленную стоимость по приобретенным ценностям:

К6 = стр. 490 / (стр. 210 + стр. 220).

Данный коэффициент показывает, какая часть запасов и затрат формируется за счет собственных средств.

3. В соответствии с полученными коэффициентами определяется значение каждого коэффициента в баллах. Согласно приложению к Методике расчета показателей финансового состояния сельскохозяйственных товаропроизводителей, утвержденной Постановлением Правительства Российской Федерации от 30 января 2003 г. N 52, общая сумма баллов является основанием для отнесения должника к одной из пяти групп финансовой устойчивости должника.

---

Порядок финансовых расчетов показателей результативности, финансовых коэффициентов ликвидности, рентабельности, финансовой устойчивости и деловой активности в корпорациях Группа компаний ИНФРА-М — Эдиторум

В материалах книги А.И. Самылина «Корпоративные финансы. Финансовые расчеты» использованы современные теории, подходы, концепции и методики финансовых расчетов в области корпоративных финансов. В учебнике, ставшем некоторым итогом исследовательской работы автора [2–19], изложены теоретические основы по рассматриваемому вопросу, дающие историческую справку по отдельным вопросам, данные о российских и зарубежных исследователях, занимавшихся данной проблемой, большой объем финансовых расчетов по управлению корпоративными финансами, а также порядок принятия менеджерами управленческих решений [1]. Такое сочетание теории и финансовых расчетов позволяет яснее понять проблему и подходы менеджеров по принятию управленческих решений. Это является важным элементом процесса обучения бакалавров и студентов, подготовки аспирантов и переподготовки специалистов.  

Излагаемый материал созвучен современным вызовам, встающим перед Россией. Переход страны на стандарты МСФО поставил ряд вопросов, касающихся анализа финансового состояния, которая составляется на основе МСФО, а в ряде случаев – и по US GAAP. Поэтому обоснованным является представленный в книге порядок финансовых расчетов показателей результативности, финансовых коэффициентов ликвидности, рентабельности, финансовой устойчивости и деловой активности не только по российским стандартам, но и по МСФО и US GAAP, а также по консолидированной финансовой отчетности. Следует отметить практическое отсутствие в настоящее время работ по финансовым расчетам по данным МСФО и US GAAP. 

Одним из путей роста стоимости компаний является их участие в проектах, реализуемых в рамках контрактной системы закупок для государственных и муниципальных нужд. Участие компаний в таких проектах позволит им подучить дополнительные источники финансирования, а студентам при изучении данного материала получить знания по способам выбора поставщиков, финансовым расчетам стоимостных критериев и цены контракта, что необходимо для формирования профессиональных специалистов в области корпоративных финансов.  

Одной из проблем экономики России является вывод капиталов в офшоры. Из этого проистекает актуальность представленного в рукописи материала о назначении офшорных зон, об участниках офшорных операций и офшорных схемах проведения финансовых операций российскими компаниями. Представленный материал затрагивает проблему коррупции и описывает мероприятия и действия государства, направленные на предотвращение вывода корпоративных финансов и капитала за рубеж. 

Значительное место в книге занимают вопросы инвестирования, проектного анализа инвестиционных проектов и обоснования выбора источников финансирования для реализации проектов. Детальный анализ методов финансирования (самофинансирование, долевое, долговое, проектное финансирование и др.), а также форм финансирования (факторинг, форфейтинг, синдицирование, внутрифирменное финансирование и др.) позволит обучаемым обоснованно выбирать источник финансирования проекта. Актуальность данных вопросов определяется проблемой реализации инвестиционных проектов для развития экономики страны и проблемой привлечения капитала.  

Возрастает объем финансовых операций российских компаний на мировом финансовом рынке. Это требует от менеджеров знаний и практических навыков по управлению корпоративными финансами с использованием форвардов, фьючерсов, свопов и опционов. Представленный большой объем примеров расчетов является важным и полезным моментом в процессе обучения. 

Российские компании все активнее выходят на мировой рынок, и поэтому изложение финансовых расчетов, связанных с корпоративными финансами по сделкам с фьючерсами, форвардами, свопами и опционами, является важным и необходимым в процессе обучения студентов. Логичным является включение в учебник материалов по дивидендной политике и финансовым расчетам сделок слияния и поглощения, что определяет сегодняшний этап в становлении российского бизнеса. 

Логичным видится представленный материал в части анализа воздействующих факторов, видов и этапов формирования дивидендной политики, выбора схем расчета и выплаты дивидендов. Эффективная дивидендная политика является важным элементом привлечения в компанию дополнительных акционеров и инвесторов, а значит, и источников финансирования.

Теоретический материал, подходы и большой объем финансовых расчетов, предлагаемые решения основываются на современных теориях, методологии, современном понятийном аппарате и отвечают принципам научности и обоснованности. Материал изложен системно, логичен по построению и методически правильно представлен, содержит ссылки на труды российских и зарубежных ученых, доступен для понимания. Все это позволит студентам, аспирантам и специалистам, глубже уяснить порядок финансовых расчетов и управления корпоративными финансами. 

Актуальным и созвучным операциям российских компаний по росту стоимости компании является рассмотрение вопросов финансовых расчетов по управлению корпоративными финансами при проведении сделок слияния и поглощения. Представленная теория вопроса дополняется финансовыми расчетами в части использования в таких сделках заемных средств схемы использования свободного денежного потока и схемы выкупа компании.  

При анализе рассматриваемых вопросов в учебнике использованы диалектический подход, метод системного анализа и др. К достоинствам книги следует отнести научность и обоснованность излагаемого материала и выводов, практические расчеты, логически связанное изложение материала, научная трактовка используемых терминов и понятий, использование современных нормативных правовых актов и доступность понимания излагаемых вопросов.

Как рассчитать и интерпретировать результат

Оглавление

Содержание

• Какой R-квадрат?

• Понимание R-квадрата

• Вычисление R-квадрата

• Часто задаваемые вопросы

• Суть

К

Скотт Невил

Полная биография

Скотт Невил — опытный внештатный писатель и редактор с подтвержденным опытом публикации контента для The Balance, Investopedia и ClearVoice. Он углубляется в создание информативного и действенного контента о денежно-кредитной политике, экономике, инвестициях, финансовых технологиях и криптовалюте. Покинув корпорацию морской пехоты США в 2014 году, он посвятил себя финансовому анализу, фундаментальному анализу и исследованиям рынка, строго придерживаясь сроков и стиля AP, а также благодаря настойчивому обеспечению качества.

Узнайте о нашем редакционная политика

Обновлено 13 апреля 2023 г.

Факт проверен

Сюзанна Квилхауг

Факт проверен Сюзанна Квилхауг

Полная биография

Сюзанна — контент-маркетолог, писатель и специалист по проверке фактов. Она имеет степень бакалавра финансов в Государственном университете Бриджуотер и помогает разрабатывать контент-стратегии для финансовых брендов.

Узнайте о нашем редакционная политика

Инвестопедия / Джули Бэнг

Что такое коэффициент детерминации?

Коэффициент детерминации — это статистическое измерение, которое исследует, как различия в одной переменной могут быть объяснены различием во второй переменной при прогнозировании исхода данного события.

Другими словами, этот коэффициент, более известный как r-квадрат (или r ² ), оценивает, насколько сильна линейная связь между двумя переменными, и инвесторы в значительной степени полагаются на него при проведении анализа тенденций.

Этот коэффициент обычно отвечает на следующий вопрос: если акция котируется в индексе и ее цена меняется, какой процент движения цены приходится на движение цены индекса?

Ключевые выводы

• Коэффициент детерминации представляет собой сложную идею, основанную на статистическом анализе данных и финансовом моделировании.
• Коэффициент детерминации используется для объяснения связи между независимой и зависимой переменной.
• Коэффициент детерминации обычно называют r-квадратом (или r ² ) из-за статистической величины, которую он представляет.
• Этот показатель представлен значением от 0,0 до 1,0, где значение 1,0 указывает на идеальную корреляцию. Таким образом, это надежная модель для будущих прогнозов, а значение 0,0 предполагает, что цены на активы не являются функцией зависимости от индекса.

R-Squared

Понимание коэффициента детерминации

Коэффициент детерминации — это мера, используемая для объяснения того, насколько изменчивость одного фактора обусловлена ​​его связью с другим фактором. Эта корреляция представлена ​​как значение от 0,0 до 1,0 (от 0% до 100%).

Значение 1,0 указывает на 100% корреляцию цен и, таким образом, является надежной моделью для будущих прогнозов. Значение 0,0 предполагает, что модель показывает, что цены не являются функцией зависимости от индекса.

Таким образом, значение 0,20 предполагает, что 20% движения цены актива можно объяснить индексом, а значение 0,50 указывает, что им можно объяснить 50% движения цены актива, и так далее.

Коэффициент детерминации представляет собой квадрат коэффициента корреляции, также известного в статистике как «r». Значение «r» может привести к отрицательному числу, но поскольку r-квадрат — это результат «r», умноженный сам на себя (или возведенный в квадрат), r ² не может дать отрицательное число — независимо от того, что найдено на Интернет — квадрат отрицательного числа всегда является положительным значением.

Расчет коэффициента детерминации

Рассчитать коэффициент детерминации. Это делается путем создания графика рассеяния данных и линии тренда.

Например, если бы вам нужно было построить цены закрытия для акций S&P 500 и Apple (Apple указана в S&P 500) для торговых дней с 21 декабря 2022 г. по 20 января 2023 г., вы бы собрали цены как показано в таблице ниже.

	Дневное закрытие S&P	APPL Ежедневное закрытие
20 января	3972,61 $	137,87 $
19	$3,898,85	135,27 $
18	3928,86 $	135,21 $
17	3990,97 $	135,94 $
13	3999,09 $	134,76 $
12	3983,17 $	133,41 $
11	3969,61 $	133,49 $
10	3 919,25 $	130,73 $
9	3 892,09 $	130,15 $
6	3 895,08 $	129,62 $
5	3 808,10 $	125,02 $
4	3 852,97 $	126,36 $
3	3 824,14 $	125,07 $
30 декабря	3 839,50 $	139,93 $
29	3 849,28 $	129,61 $
28	3783,22 $	126,04 $
27	3 829,25 $	130,03 $
23	3 844,82 $	131,86 $
22	3 822,39 $	132,23 $
21	3 878,44 $	135,45 $

Затем вы должны создать точечную диаграмму. На графике то, насколько хорошо данные соответствуют регрессионной модели, называется 9.0274 качество подгонки, , которое измеряет расстояние между линией тренда и всеми точками данных, разбросанными по всей диаграмме.

Электронные таблицы

В большинстве электронных таблиц используется одна и та же формула для расчета r

2 набора данных. Итак, если данные находятся в столбцах A и B на вашем листе:

= RSQ (A1: A10, B1: B10)

Используя эту формулу и выделив соответствующие ячейки для цен S&P 500 и Apple, вы получите r ² на уровне 0,347, что позволяет предположить, что две цены менее коррелированы, чем если бы r ² находился в диапазоне от 0,5 до 1,0.

Расчет вручную

Расчет коэффициента детерминации вручную включает несколько этапов. Сначала вы собираете данные, как в предыдущей таблице. Во-вторых, вам нужно рассчитать все необходимые значения, как показано в этой таблице, где:

• x= дневное закрытие S&P 500
• y = дневное закрытие APPL

	х	x2	и	у2	ху
20 января	3972,61 $	$15 781 630,21	137,87 $	19 008,14 $	$547 703,74
19	3 898,85 $	$15 201 031,32	135,27 $	$18 297,97	$527 397,44
18	3928,86 $	$15 435 940,90	135,21 $	$18 281,74	531 221,16 $
17	3990,97 $	$15 927 841,54	135,94 $	$18 479,68	$542 532,46
13	3999,09 $	$15 992 720,83	134,76 $	$18 160,26	$538 917,37
12	3983,17 $	$15 865 643,25	133,41 $	$17 798,23	$531 394,71
11	3969,61 $	$15 757 803,55	133,49 $	$17 819,58	$529 903,24
10	3 919,25 $	15 360 520,56 $	130,73 $	17 090,33 $	$512 363,55
9	3 892,09 $	$15 148 364,57	130,15 $	16 939,02 $	$506 555,51
6	3 895,08 $	$15 171 648,21	129,62 $	16 801,34 $	$504 880,27
5	3 808,10 $	$14 501 625,61	125,02 $	$15 630,00	476 088,66 $
4	3 852,97 $	$14 845 377,82	126,36 $	$15 966,85	486 861,29 $
3	3 824,14 $	$14 624 046,74	125,07 $	$15 642,50	478 285,19 $
30 декабря	3 839,50 $	$14 741 760,25	139,93 $	$19 580,40	$537 261,24
29	3 849,28 $	$14 816 956,52	129,61 $	$16 798,75	498 905,18 $
28	3783,22 $	$14 312 753,57	126,04 $	15 886,08 $	476 837,05 $
27	3 829,25 $	$14 663 155,56	130,03 $	16 907,80 $	497 917,38 $
23	3 844,82 $	$14 782 640,83	131,86 $	17 387,06 $	$506 977,97
22	3 822,39 $	$14 610 665,31	132,23 $	$17 484,77	$505 434,63
21	3 878,44 $	$15 042 296,83	135,45 $	$18 346,70	$525 334,70
Сумма (Σ)	77 781,69 $	$302 584 424,00	2 638,05 $	$348 307,23	$10 262 772,73

Далее используйте эту формулу и подставьте значения для каждой строки таблицы, где 92 \\\конец{выровнено} r2=([20(302 584 424)−(77 781,69)2]×[20(348 307,23)−(2 638,05)2]​20(10 262 772,73)−(77 781,69)(2 638,05)​)2​

Итак, теперь у вас есть :

1. ( 20 × 10 , 262 , 772,73 ) − ( 77 , 781,69 × 2 , 638.05 ) «=» 63 , 467,32 2. ( ( 20 × 302 , 584 , 424 ) − ( 77 , 781,69 ) 2 «=» 1 , 697 , 180,74 «=» 1 , 302,76 3. ( ( 20 × 10 , 262 , 772,73 ) − ( 2 , 638.05 ) 2 «=» 6 , 836,85 «=» 82,69 \begin{выровнено}&1. \ крошечный { ( 20 \ умножить на 10 262 772,73 ) — ( 77 781,692 = 0,347\конец{выровнено} ​(1 302,76 × 82,6963 467,32​)2=0,347​

Вы можете видеть, как это может стать очень утомительным с большим количеством места для ошибок, особенно если вы используете более чем несколько недель торговых данных.

Интерпретация коэффициента детерминации

Когда у вас есть коэффициент детерминации, вы используете его для оценки того, насколько близко движение цены оцениваемого актива соответствует движению цены индекса или эталона. В примере с Apple и S&P 500 коэффициент детерминации для периода составил 0,347.

Поскольку 1,0 демонстрирует высокую корреляцию, а 0,0 — отсутствие корреляции, 0,357 показывает, что движения цен на акции Apple в некоторой степени коррелируют с индексом.

Apple котируется во многих индексах, поэтому вы можете рассчитать r ² , чтобы определить, соответствует ли оно движениям цен любых других индексов.

Один аспект, который следует учитывать, заключается в том, что r-квадрат не говорит аналитикам, является ли значение коэффициента детерминации хорошим или плохим по своей сути. Они могут по своему усмотрению оценить значение этой корреляции и то, как ее можно применить в будущем анализе тенденций.

Как интерпретировать коэффициент детерминации?

Коэффициент детерминации показывает, насколько взаимосвязаны одна зависимая и одна независимая переменные. Также называется r ² (r-квадрат), значение должно находиться в диапазоне от 0,0 до 1,0. Чем ближе к 0,0, тем меньше коррелирует зависимое значение. Чем ближе к 1,0, тем больше коррелирует значение.

Что R-квадрат говорит вам в регрессии?

Сообщает вам, есть ли зависимость между двумя значениями и насколько сильно одно значение зависит от другого.

Что делать, если коэффициент детерминации больше 1?

Коэффициент детерминации не может быть больше единицы, поскольку формула всегда дает число от 0,0 до 1,0. Если он больше или меньше этих цифр, что-то не так.

Суть

Коэффициент детерминации — это отношение, показывающее, насколько одна переменная зависит от другой переменной. Инвесторы используют его, чтобы определить, насколько движение цены актива коррелирует с его котируемым индексом.

Когда r ² актива ближе к нулю, он не демонстрирует зависимости от индекса; если его r ² ближе к 1,0, он больше зависит от движения цены, которое делает индекс.

Источники статей

Investopedia требует, чтобы авторы использовали первоисточники для поддержки своей работы. К ним относятся официальные документы, правительственные данные, оригинальные отчеты и интервью с отраслевыми экспертами. Мы также при необходимости ссылаемся на оригинальные исследования других авторитетных издателей. Вы можете узнать больше о стандартах, которым мы следуем при создании точного и беспристрастного контента, в нашем редакционная политика.

1. Насдак. «Исторические данные APPL».

2. Насдак. «Исторические данные SPX».

Как рассчитать коэффициент корреляции (с примерами)

Корреляция не подразумевает причинно-следственной связи.

Это часто используемая фраза, которую вы, скорее всего, слышали в тот или иной момент. Это означает, что причинно-следственная связь не может быть определена только потому, что существует некоторая наблюдаемая корреляция между двумя переменными.

Мы не можем сделать вывод о причинно-следственной связи просто потому, что существует некоторая степень корреляции.

Мы можем заметить, что те, кто уделяет много внимания корпусу во время тренировок, теряют жир на животе. Потеря жира может произойти в результате тренировки больше, чем обычно; это не обязательно связано с основной работой.

Вы когда-нибудь задумывались, откуда взялась эта фраза? Если вы статистик или знакомы с коэффициентом корреляции, то вы уже знаете.

Несмотря на использование в популярной культуре, эта фраза напрямую связана с коэффициентом корреляции.

Основные выводы:

• Коэффициент корреляции измеряет, насколько сильна линейная связь между двумя переменными.

• Корреляция «произведение-момент» Пирсона является наиболее распространенным методом определения корреляции.

• Коэффициент корреляции между 0 и 1 указывает на положительную связь, а значение 1 означает идеальную корреляцию.

• Коэффициент корреляции от 0 до -1 указывает на отрицательную связь, а значение -1 означает идеальную корреляцию.

• Коэффициент корреляции, равный 0, указывает на отсутствие линейной зависимости и, вероятно, на отсутствие корреляции.

• Что такое коэффициент корреляции?
• Pearson Product-Moment Correlation (PPMC)
• Что такое ковариация и стандартное отклонение?
• Понимание ваших результатов
• Что означает сила коэффициента корреляции?
• Тринадцать способов интерпретации коэффициента корреляции
• Недостатки коэффициента корреляции
• Коэффициент корреляции в реальных жизненных ситуациях
• Зарегистрируйтесь для получения дополнительных советов и вакансий

Показать больше

Что такое коэффициент корреляции?

Коэффициент корреляции — это статистическая мера того, насколько сильна линейная связь между двумя переменными.

Корреляция основана на данных наблюдений, поэтому, хотя мы можем определить сильную взаимосвязь между двумя переменными, это не обязательно указывает на то, что одна является причиной другой.

Таким образом, фраза «корреляция не подразумевает причинно-следственную связь».

Для расчета коэффициента корреляции вам потребуется числовое значение, представляющее каждую переменную, ваш «X» и ваш «Y».

В данных не должно быть выбросов; ассоциация должна быть полностью линейной.

Корреляция продукта и момента Пирсона (PPMC)

Корреляция продукта и момента Пирсона, чаще называемая коэффициентом корреляции Пирсона, является наиболее распространенным методом определения корреляции. Этот метод был разработан в 189 г.5 Карла Пирсона, британского статистика, которого считают отцом-основателем современной статистики.

Формула выглядит так:

nΣxy – ΣxΣy
√ [nΣx ² – (Σx) ² ] [nΣy ² – (Σy) ² ]

Если вы когда-нибудь проходили курс статистики или ранее рассчитывали коэффициенты корреляции, то, скорее всего, сталкивались с коэффициентом корреляции Пирсона.

К счастью, для тех, кто не так склонен к математике, все базовые программы для работы с электронными таблицами и статистические приложения имеют функции корреляции для вычисления этой формулы. Калькуляторы TI 83 могут найти коэффициент корреляции с правильной функцией. Вы также можете найти множество готовых калькуляторов, доступных во всемирной паутине.

Если вы хотите или должны рассчитать коэффициент корреляции вручную, выполните следующие действия.

1. Составьте диаграмму. Так же, как и в электронной таблице, вам необходимо составить схему всей информации. Вы хотите включить столбец для вашей переменной x, вашей переменной y, xy, x ² и y ² . Используя полученную информацию, заполните таблицу.

2. Найдите Σ для каждого столбца. Это была бы формула суммы в Excel, если бы мы использовали электронную таблицу. Найдите сумму каждого столбца и поместите ее внизу соответствующего столбца.

3. Найдите результат. Чтобы найти коэффициент корреляции Пирсона r, необходимо заполнить формулу. Эта формула делится на числитель и знаменатель.

   Числитель состоит из следующего уравнения:

   nΣxy – ΣxΣy

   Знаменатель состоит из следующего уравнения:

   √ [nΣx ² – (Σx) ² ] [nΣy ² – (Σy) ² ]

   В полной форме это выглядит так:

   nΣxy – ΣxΣy
   √ [nΣx ² – (Σx) ² ] [nΣy ² – (Σy) ² ]

   n — это количество значений, которые у вас есть. Σ — это символ сигмы, который используется в математике для обозначения суммы нескольких членов.

Независимо от того, как запускается формула, процесс и результаты будут одинаковыми.

Что такое ковариация и стандартное отклонение?

Некоторые дополнительные термины, которые следует знать при расчете коэффициента корреляции, — это ковариация и стандартное отклонение.

• Ковариация. Ковариация — это мера того, как две переменные изменяются вместе. Он указывает направление линейной зависимости или является ли она положительной или отрицательной связью. Поскольку корреляция указывает как направление, так и силу, для нахождения коэффициента корреляции необходимо найти ковариацию.

• Стандартное отклонение. Стандартное отклонение — это мера изменчивости. Высокая изменчивость подразумевает большее отклонение значений от их среднего значения.

Коэффициент корреляции можно определить, разделив ковариацию переменных на их стандартные отклонения.

После того, как формула вернет коэффициент корреляции r, можно определить взаимосвязь. Формула PPMC возвращает значение от -1 до 1. Чем выше число, тем сильнее связь.

Понимание ваших результатов

Абсолютное значение результата покажет, насколько сильны отношения, но есть только три возможных результата.

1. Положительные отношения. Значение больше нуля указывает на положительную связь. Это означает, что при увеличении значения одной переменной значение второй переменной также увеличивается.

   На линейном графике показан восходящий наклон слева направо.

   Пример ответа 1:

   Чем больше часов вы работаете, тем выше будет ваша зарплата.

   Пример ответа 2:

   По мере роста ребенка растет и размер его обуви.

2. Отрицательное отношение. Значение меньше нуля указывает на отрицательную связь. Мы видим, что значение одной переменной увеличивается с отрицательными отношениями, в то время как значение другой переменной уменьшается.

   На линейном графике будет показан нисходящий наклон слева направо.

   Пример ответа 1:

   Чем медленнее вы едете, тем дольше продлится ваша поездка.

   Пример ответа 2:

   Чем больше вы тренируетесь, тем меньше вы будете весить.

3. Нет связи. Нулевое значение указывает на отсутствие связи между переменными. Две переменные никак не влияют друг на друга, если формула возвращает результат 0. Увеличение или уменьшение одной переменной не приведет к увеличению или уменьшению другой переменной.

   Неправильный линейный график.

   Пример ответа 1:

   Количество выпитого чая в зависимости от того, насколько они британцы.

   Пример ответа 2:

   Цена на шоколад против цены на хлопья.

Что означает сила коэффициента корреляции?

Кафедра политологии Квиннипиакского университета предоставила «грубые оценки» для интерпретации силы корреляции с использованием результата абсолютного значения коэффициента корреляции Пирсона.

Взяв абсолютное значение результата, вы можете определить силу связи между двумя переменными. Чем ближе коэффициент корреляции Пирсона r к 1, тем сильнее связь.

• .70+ — очень сильная связь

• от 0,40 до 0,69 — сильная связь

• от 0,30 до 0,39 — умеренное соотношение

• от 0,20 до 0,29 — слабая связь

• от 0,01 до 0,19— нет или незначительна связь

• 0 — нет связи

Тринадцать способов интерпретации коэффициента корреляции

Джозеф Ли Роджерс и Алан Найсвандер в 1988 году представили в «The American Statistician» статью, в которой обсуждалось, как можно взглянуть на коэффициент корреляции. Они следующие:

1. Корреляция как функция необработанных баллов и средних значений

2. Корреляция как стандартизированная ковариация

3. Корреляция как стандартизованный наклон линии регрессии

4. Корреляция как среднее геометрическое двух наклонов регрессии

5. Корреляция как квадратный корень из отношения двух дисперсий

6. Корреляция как среднее перекрестное произведение стандартизированных переменных

7. Корреляция как функция угла между двумя стандартизированными линиями регрессии

8. Корреляция как функция угла между двумя переменными векторами

9. Корреляция как пересчитанная дисперсия разницы между стандартизированными баллами

10. Корреляция, оцененная по правилу шара

11. Корреляция по отношению к двумерным эллипсам изоконцентрации

12. Корреляция как функция тестовой статистики из разработанных экспериментов

13. Корреляция как отношение двух средних

Недостатки коэффициента корреляции

Вернемся к «корреляция не подразумевает причинно-следственной связи».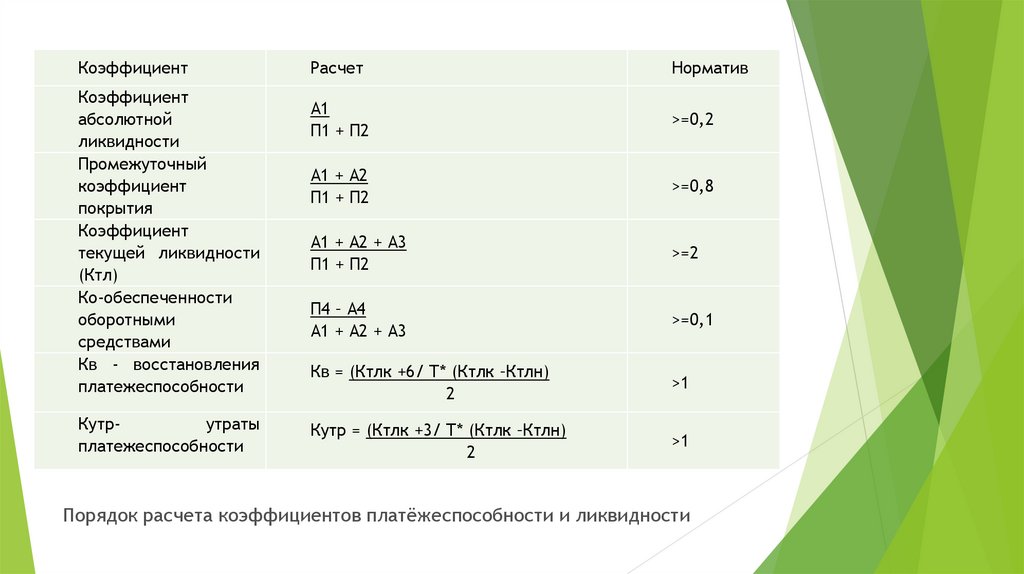 Коэффициент корреляции Пирсона не может различать зависимые переменные и независимые переменные. Проще говоря, причина и следствие.

Результаты, полученные по этой формуле, могут только определить, существует ли взаимосвязь. К сожалению, это означает, что результаты могут быть ошибочными.

Сильная корреляция между переменными не обязательно означает, что одна является причиной другой.

Аналогично, нулевая корреляция не обязательно означает отсутствие связи. Связь между двумя переменными может быть просто нелинейной. Коэффициент корреляции Пирсона не может отражать нелинейные отношения.

Также часто могут возникать иллюзорные корреляции или ложные корреляции. Нередко считается, что между двумя переменными существует связь, несмотря на то, что ее нет. Полнолуния вызывают сумасшедшее поведение — обычная иллюзорная корреляция.

Коэффициент корреляции в реальных жизненных ситуациях

Конечно, это красивая математика. Когда вы собираетесь использовать это вне класса? Никогда, верно?

Возможно. Но это может быть неправильно. Все зависит от того, какую карьеру вы выберете. Ваша работа и отрасль могут часто использовать коэффициент корреляции.

Во многих отраслях регулярно применяется коэффициент корреляции и его результаты:

1. Страхование. Страховые компании рассчитывают свои ставки на основе коэффициентов корреляции. У них разные ставки в зависимости от возраста, пола, местонахождения и т. д. потенциального клиента.

2. Запасы. Использование коэффициента корреляции является обычным явлением при инвестировании. Это позволяет вам разработать надежную инвестиционную стратегию и чрезвычайно полезно при принятии решения о том, в какие акции инвестировать.

   Инвесторы часто используют отрицательную корреляцию для диверсификации своих портфелей. Они могут выбрать комбинацию акций с положительной и отрицательной корреляцией с разной степенью силы, чтобы еще больше диверсифицировать. Коэффициент корреляции также используется для расчета волатильности портфеля.