Совместительство и совмещение разница: Совмещение и совместительство, в чем разница

Совместительство и совмещение разница: Совмещение и совместительство, в чем разница

Совместительство и совмещение должностей. В чем разница?

В чем разница между совместителем и совмещением должностей?

В пп. 56) п.1 статьи 1 Трудового Кодекса Республики Казахстан определено, что совместительство – это выполнение работником другой регулярной оплачиваемой работы на условиях трудового договора в свободное от основной работы время.

   Согласно п. 4 статьи 32 Трудового Кодекса Республики Казахстан для заключения трудового договора о работе по совместительству с другим работодателем работник представляет справку о характере и условиях труда по основному месту работы (место работы, должность, условия труда).

   В соответствии с п. 3 статьи 68 Трудового Кодекса Республики Казахстан суммарная продолжительность ежедневной работы по месту основной работы и работы по совместительству не должна превышать норму продолжительности ежедневной работы, установленную пунктом 4 статьи 71 Трудового Кодекса, более чем на 4 часа.

    В пп.1) п. 2 статьи 111 Трудового Кодекса Республики Казахстан указано, что совмещения должностей – это выполнения работником наряду со своей основной работой, предусмотренной трудовым договором (должностной инструкцией), дополнительной работы по другой вакантной должности.

     Согласно п.1 статьи 111 Трудового Кодекса Республики Казахстан работникам, выполняющим в одной и той же организации наряду со своей основной работой, обусловленной трудовым договором, дополнительную работу по другой или такой же должности либо обязанности временно отсутствующего работника без освобождения от своей основной работы, производится доплата.

       Следовательно, работа на условиях совместительства осуществляется на основе отдельного заключенного трудового договора, который может быть заключен как с работодателем, с которым у работника уже имеется заключенный трудовой договор на основную работу (внутреннее совместительство) так и может быть заключен договор с другим работодателем (внешнее совместительство).

При работе на условиях совместительства устанавливается заработная плата. Работа на условиях совместительства как внутреннего, так и внешнего осуществляется за пределами рабочего времени по основной работе, то есть за пределами 8-часового рабочего дня. При этом общее продолжительность ежедневной работы по месту основной работы и работы по совместительству не должна превышать 12 часов (8-ми часовой рабочий день по основной работе + 4 часа по совместительству). 

При совмещении должностей работник выполняет дополнительную работу в пределах рабочего времени по основной работе.  То есть работник выполняет работу как основную, так и дополнительную работу по совмещаемой должности в пределах 8-ми часового рабочего дня. За совмещение должностей работнику устанавливают доплату.

#совместитель #совместительство #совмещениедолжностей #совмещениедолжностейзарплата #учетсовместительство #расчетзарплаты #зарплатасовместитель #icfm.kz

Вернуться назад

плюсы и минусы для работника и работодателя

Трудовое законодательство в теории четко различает понятия совмещение и совместительство, но на практике зачастую возникает множество вопросов. Тем не менее их решение обязательно, поскольку от этого зависят такие важные факторы как расчет будущей пенсии, продолжительность отпуска и его оплата, больничный лист.

Для обывателя разница между двумя этими понятиями не так очевидна, поскольку их смысл заключается в выполнении некоторых трудовых функций кроме имеющейся постоянной занятости.

Понятие «совместительство»

Совместительство – это выполнение исполнителем регулярной деятельности, условия которой регламентированы заключенным Трудовым договором, в свободное от постоянной занятости время. Каждый человек может найти дополнительный заработок, выполнение функций для которого, не мешает выполнению своих основных трудовых обязанностей. Регламент подобных отношений закреплен в Трудовом Кодексе в ст.44, 60.1, 282—288.

К сведению

При оформлении обязательно издается приказ, а запись в трудовую книжку вносят по желанию работника. Обязательно на втором месте работы оформляется личная карточка.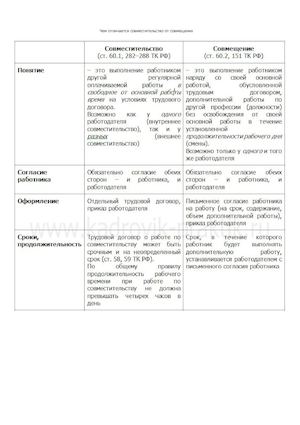 Руководителя, который выступает в качестве нового работодателя, необходимо заранее предупредить, что данная деятельность в организации будет являться совместительством.

Для оформления требуется весь набор документов, подтверждающий личность, наработанный стаж и имеющийся опыт, а также реквизиты, необходимые бухгалтерии, для перевода заработной платы: паспорт, ИНН, диплом и т.д.

Период таких отношений устанавливается на конкретный ограниченный срок или является бессрочным. Ежедневное время исполнения дополнительных функций не должно быть более 4 часов, и 8 часов в следующих случаях: выходной день по основному месту занятости, либо временное отстранение от постоянной работы или приостановление выполнения функций. Превышение допустимого лимита труда может влечет административную ответственность руководителя.

Оплата труда чаще всего повременная или сдельная, но соглашением может быть предусмотрен и иной вариант.

Внимание

Законодательством предусмотрены ограничения, которые запрещают работать по совместительству некоторым категориям лиц, а именно несовершеннолетним и представителям некоторых профессий: например, муниципальные и госслужащие, охранники, военнослужащие, сотрудники органов правопорядка, судьи и т.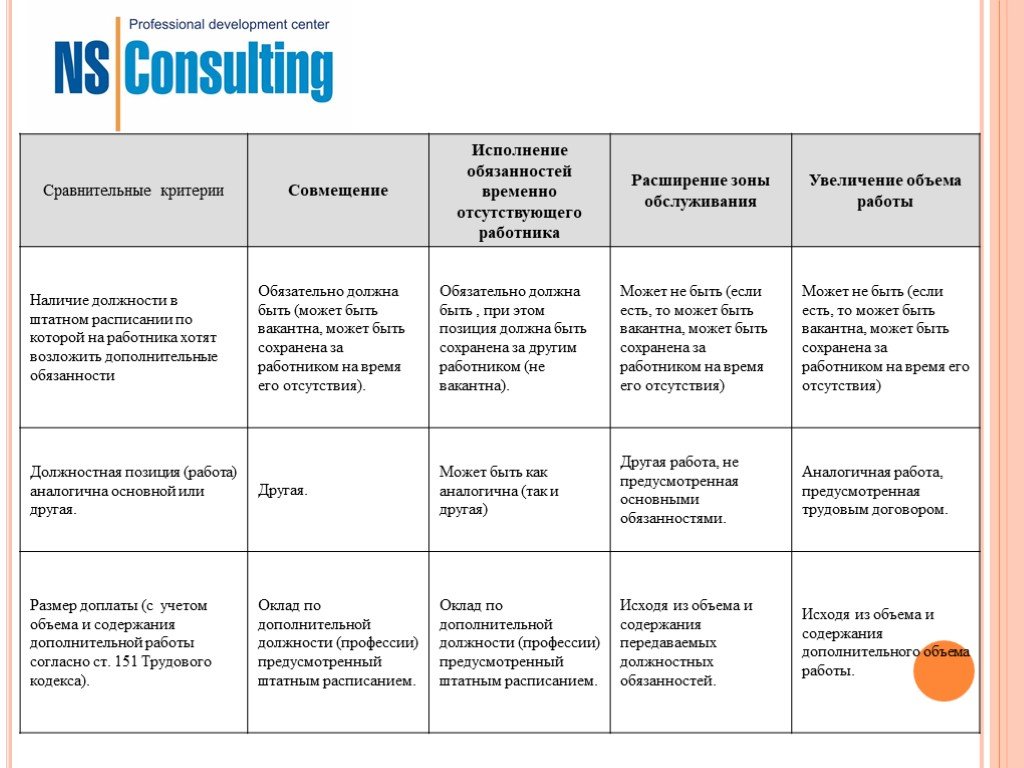 д.

Совместительство, согласно ст. 60.1 ТК, может быть двух видов:

• внутреннее – в этом случае выполнение дополнительных функций осуществляется в той же организации, где заключен основной Трудовой договор;
• внешнее – означает исполнение трудовых обязанностей на другом предприятии.

При нарушении условий оформления новый руководитель, совершивший нарушение единожды, привлекается к административному наказанию, повторный проступок влечет за собой дисквалификацию. Для сотрудника же это грозит увольнением с основного места.

Дополнительная информация

Прекращение действия Трудового договора происходит в соответствии с общими положениями трудового законодательства.

Понятие «совмещение»

Совмещение — означает увеличение объемов работы определенного работника или зоны его обслуживания по своему постоянному месту работы. Порученные работодателем дополнительные задачи подлежат исполнению в течении установленного периода рабочего дня, не отрываясь при этом от постоянных обязанностей. Определенная профессия или должность, задачи которой будут выполняться, может как совпадать с основной занятостью, так и нет. Стоит учесть, что в данном случае продолжительность основного рабочего времени не должна быть превышена.

К сведению

Трудовые отношения при таком варианте подработки регулирует Трудовой Кодекс статьями 60.2 и 151. Обычно, предложение об увеличении объема выполняемых функций поступает со стороны руководства, а работник уже принимает решение о согласии или отказе.

Для начала трудовых отношений оформляется письменное соглашение к уже имеющемуся ТД, а также издается приказ о приеме и согласие работника в письменном виде. Помимо этих документов, требуется только внесение сведений в уже имеющуюся личную карточку исполнителя. Обязательным условием является наличие вакантной должности в штате организации.

В обязательном письменном соглашении между сторонами прописываются должность или профессия для совмещения, перечень функций, их объем и срок выполнения, предусмотренная доплата. Чаще всего подобным образом оформляются сотрудники, коллеги которых ушли в отпуск, на больничный, либо в декрет.

Дополнительная информация

Размер производимой доплаты должен быть указан в соглашении. При начислении все действующие надбавки и коэффициенты не учитываются. Срок действия соглашения может быть установлен, либо прекращается в момент выхода основного работника. К тому же, возможен вариант преждевременного расторжения соглашения по инициативе любой стороны. Для этого необходимо поставить другую сторону в известность за 3 дня до прекращения работ.

Виды совмещения

Поскольку подобная процедура совмещения на отечественных предприятиях достаточно широко распространена, выделяют сразу несколько видов:

1. Совмещение нескольких профессий или должностей – например, завхоз выполняет задачи и кладовщика. Этот вид может быть предложен неожиданно, либо предусмотрен заранее. В первом случае, оформляется письменное соглашение. Во втором случае при подписании Трудового договора, следует внимательно его читать, поскольку одним из пунктов может быть именно условие о совмещении. Это установлено ТК РФ в ст. 57.
2. Увеличение зоны обслуживания или объема работ – например, исполнение функций по соседнему участку. Этот вид также может иметь временный или постоянный характер, и любая сторона имеет право отказаться от поставленных условий.
3. Замещение временно отсутствующих – предусматривает замену на определенный промежуток времени работника, который отсутствует по уважительной причине: отпуск, больничный и т.д. Как видно из самого названия, замена имеет временный характер, до выхода основного работника.

Все это предусмотрено в ТК РФ, ст. 60.2.

Разница внутреннего совместительства и совмещения

Внутреннее трудоустройство в любом из этих случаев, предполагает выполнение работ в организации по основной занятости. Руководители часто стараются найти временную замену или распределить функции между уже устроенными сотрудниками. Для работодателя это более удобно, и достаточно частым являются случаи, когда доплачивать за увеличение объема работ вовсе не хочется.

Внимание

В случае, если неожиданно у работника появляются новые функции нужно как следует изучить собственную должностную инструкцию, поскольку велика вероятность, что за их выполнение можно получить доплату.

Существенные различия заключаются в следующем:

• оформление – в первом варианте необходимо заключение нового ТД, во втором – нет;
• испытательный срок – в первом варианте может быть, во втором – отсутствует;
• запись в трудовой книжке делают только при совместительстве;
• оплата труда в первом случае осуществляется по фактически отработанному времени с сохранением предусмотренных коэффициентов, а во втором – за выполненные функции.

Какой именно из возможных вариантов будет оформлен достаточно важно, особенно для исполнителя.

 Различия совмещения и совместительства

Существенные различия этих двух понятий можно отследить сразу по нескольким критериям.

Условие	Совместительство	Совмещение
Место труда	Любая организация, в том числе и место постоянной занятости	Место постоянной занятости, где сотрудник уже работает
Трудовой договор	ТД заключается на различные сроки	Поскольку ТД уже заключен, новый не требуется. К нему прилагают письменное соглашение, где прописан период выполнения дополнительных обязанностей, а также их объем.
Испытательный срок	Есть, и он может быть разной продолжительности, конкретный срок оговаривается на собеседовании	Отсутствует
Оформление	Форма N Т-1	Издается только приказ о назначении
Трудовая книжка	Запись по основному месту	Не делают
Личная карточка и дело	При внешнем – оформляют то и другое, если же, внутреннее – заводят только личную карточку	Эти документы уже есть, поэтому в карточку просто вносят дополнительные сведения
Оплата труда	Оплата осуществляется в согласно ТД, и зависит от выработки и фактически отработанном времени. Если за выполняемую работу предусмотрены коэффициенты или надбавки — они применяются при начислении	Размер оплаты указывается в соглашении и выплачивается в виде доплаты, при этом надбавки или коэффициенты не учитываются
Отпуск	Его период совпадает с отпуском по основному месту	Отпускной период остается прежним, но при начислении отпускных выполняется доплата
Продолжительность рабочего дня	Не больше 4 часов ежедневно, либо до 8 часов в выходные дни от постоянной занятости	Длится столько же, сколько и основной рабочий день
Пособия по больничным листам	Оформляется и рассчитывается сразу в 2-х организациях	Размер пособия зависит от суммы основного заработка с доплатами
Сроки прекращения	Согласно ст. 81, ТК РФ	Срок окончания совмещения указан в соглашении. Обе стороны имеют право прекратить трудовые отношения по совмещению досрочно, уведомив об этом за 3 дня до этого.

К сведению

Таким образом, можно понять, что разница не только в самих понятиях и выгодах для работниках, а также в юридическом и документальном оформлении.

Что выбрать работодателю?

Для работодателя наиболее выгодным вариантом является совмещение. Для этого нет необходимости тратить время и деньги на поиск замены, тем более, если есть необходимость в этом только на короткий срок. При этом квалификация и профессиональные качества уже работающего сотрудника известны. В этом случае работодатель получает только плюсы, выражающиеся в рациональном распределении ресурсов, сокращении налогооблагаемой базы и экономия на заработной плате и самом процессе подбора персонала.

Внимание

Стоит учитывать, что при длительном совмещении, возможно снижение качества выполняемой работы по одной из должности.

Совместительство часто применяется для высококвалифицированных профессионалов, полноценные услуги которых стоят очень дорого и, в которых, нет постоянной необходимости. Например, главный бухгалтер, юридический консультант и т.д. В данном случае работодатель получает отличный результат за сравнительно небольшие деньги.

Что выбрать работнику?

Для работника каждый вид подработки несет определенные преимущества и недостатки.

Плюсы совместительства:

• заработная плата выше, чем при совмещении;
• работа в разных организациях выгоднее, в случае прекращения деятельности одной из них или увольнения работника;
• получение всех, предусмотренных государством, гарантий – отпуск, больничный и т.д. в 2-х местах;
• такой вариант позволяет меньше уставать, поскольку имеет место смена деятельности, а также развитие новых знаний и получение опыта.

Плюсы совмещения:

• непродолжительность подработки, что позволяет не слишком устать;
• продолжительность рабочего дня при этом не увеличивается;
• освободив руководителя от поиска замены, можно обрести дополнительный авторитет в его глазах и проявить свои лучшие качества;
• возможность заработать дополнительные средства в своей же организации;
• увеличение выплат по больничным листам и отпускам;
• нет необходимости тратить время и деньги на проезд до другого места работы.

Зная их, можно легко определиться, какой именно вариант наиболее приемлем в каждом конкретном случае. Но так как достоинства есть в обоих вариантах, то приемлемы они оба. Может быть, для кого-то определяющим критерием является больший заработок, а для другого – важно наличие свободного времени и отсутствие необходимости ездить с места на место.

Нюансы

Трудовой Кодекс — определяющий документ в регулировании трудовых отношений между работодателем и сотрудником, поэтому даже при наличии дополнительных функций требуется соблюдение всех установленных норм, будь то продолжительность рабочего дня, либо правила внутреннего распорядка. Поэтому при увеличении нагрузки следует правильно рассчитать свои силы и возможности, ведь исполнитель сам принимает решение о согласии или отказе от дополнительного заработка.

Дополнительная информация

Помимо статей 60.1 и 60.2 эти виды трудовых отношений регулируются и другими, например, 282. Помимо этого, деятельность представителей некоторых специальностей подчиняется, например, Закону об образовании или Федеральным законам, гласящим о какой-либо отдельной отрасли.

Для специальностей, по которым есть ограничения в сфере дополнительных работ, существуют и оговорки. Например, работники медицины, образования и культуры имеют право выполнять разовые экспертные оценки, либо определенный объем почасовых работ и т.д.

Знание особенностей разных видов трудовых отношений позволит исполнителю найти дополнительный источник заработка, а также избежать неожиданных или неприятных сюрпризов.

Знайте о разнице между перестановкой и комбинацией

Перестановка и комбинация являются важными частями подсчета. Подсчет чисел с помощью чистой логики сам по себе является большой задачей. Без подсчета мы не можем решить вероятностные задачи. Вот почему мы изучаем перестановки и комбинации непосредственно перед вероятностью.

 

Здесь мы увидим, как различать перестановку и комбинацию, в чем разница между комбинацией и перестановкой и разница между перестановкой и комбинацией на различных примерах.

 

Что такое перестановка?

Перестановка — это процесс выбора, в котором порядок имеет значение. Перестановку можно просто определить как количество способов упорядочить несколько или все элементы в определенном порядке. Это все о термине Перестановка.

 

Пример. Перестановки букв в небольшом наборе {a, b, c}: а набор или группа n. Обычно это записывается в \[nP_k\].

 

Формула:

\[nP_{k} = \frac{n!}{(n — k)!} = \frac{n(n−1)(n−2)\ldots(n−n +1)}{(n-k)(n-k−1)(n-k−2)\ldots(n-k−n-k+1)} \]

 

Существует два типа перестановок:

1. Перестановки с повторением

При выборе r чего-либо (числа или любого элемента), имеющего n различных типов, перестановки будут следующими:

\[n \times n \times \ldots\] (r times)

нет возможностей для первого процесса выбора, ТОГДА нет возможностей для второго процесса выбора и т. д., и каждый раз умножается.) 9{r}\]

, где n — количество элементов для выбора (т. е. набор или сток элементов), и мы выбираем r из них, повторение разрешено, и порядок имеет значение.

2. Перестановки без повторения

Без повторения наш выбор каждый раз уменьшается.

 

Возьмем самый простой и широко используемый пример:                   

Сколько различных четырехкарточных комбинаций можно составить из колоды карт?

 

В этой задаче порядок не имеет значения, так как не имеет значения, в каком порядке мы выбираем карты. Мы начинаем с четырех строк, чтобы представить нашу комбинацию из 4 карт.

 

Предполагая, что все 52 карты доступны для первого розыгрыша, поместите «52» в первый пробел. Когда вы выбираете карту, это означает, что одна карта уже выбрана, поэтому в следующем розыгрыше выбора будет на одну карту меньше. Таким образом, во втором бланке будет доступен 51 вариант. Кроме того, в следующем розыгрыше в колоде будет на две карты меньше, так что теперь есть 50 вариантов и так далее. Формула написана:

\[P\binom{n}{r} = nP_{r} = \frac{n!}{(n — k)!} \]

По формуле получаем

\[P\binom{ 52}{4} = 52P_{4} = \frac{52!}{48!} \]

, где n — количество элементов, из которых можно выбирать (т. е. набор или сток элементов), и мы выбираем r из их, никаких повторений и порядок имеет значение.

 

Что такое комбинация?

Комбинация — это способ выбора элементов из большой коллекции, при котором (непохожие перестановки) порядок выбора не имеет значения. Мы можем сказать, что в меньших случаях мы сможем подсчитать количество комбинаций. Комбинация относится к комбинации n вещей, взятых k за раз без повторений. Комбинация — это выбор r вещей из набора n вещей без замены и порядок не имеет значения.

 

\[C\binom{n}{r} = nC_{r} =\frac{nP_r}{r!} = \frac{n!}{r!(n — k)!} \]

Давайте возьмем пример и поймем это,

 

У нас есть три цифры (1,2,3), и мы хотим сделать трехзначное число, Таким образом, следующие числа, которые будут возможны, это 123, 132, 213, 231, 312, 321..

 

Комбинации дают нам простой способ вычислить, сколькими способами можно расположить «1 2 3» в определенном порядке, и мы это уже видели. Ответ:

 

3! = 3 \[\times\] 2 \[\times\] 1 = 6

 

Таким образом, мы перепечатываем формулу нашей Перестановки, чтобы сократить ее количество способов, которыми объекты могут быть упорядочены (поскольку нас не интересует их закажи еще).

 

Разница между перестановкой и комбинацией с примерами

Получить разницу между перестановкой и комбинацией не слишком легко и не слишком сложно. Мы рассмотрим несколько примеров, чтобы понять разницу между ними.

Перестановки

• Расположение людей, цифр, чисел, алфавитов, букв и цветов и т. д.

• Выбор капитана команды или вратаря и конкретного из группы.

• Выбор двух любимых цветов по порядку из каталога цветов.

• Выбор победителей первого, второго и третьего призов.

 

Комбинации

• Выбор меню, еды, одежды, тематики, команды и т. д.

• Выбор трех членов команды из группы.

• Выбор двух цветов из каталога цветов.

• Только три победителя.

 

Как отличить перестановку от комбинации

Перестановки и комбинации относятся к различным способам выбора объектов из набора, как правило, без замены, для формирования подмножеств (или мы можем сказать количество подмножеств). за комплект). Этот выбор подмножеств называется перестановкой, когда порядок выбора является фактором, и комбинацией, когда порядок не является фактором. (Проще говоря, выбор подмножеств — это перестановка, а не дробный порядок выбора называется комбинацией).

 

Сходства между перестановкой и комбинацией

С точки зрения математических понятий «перестановка» и «комбинация» связаны друг с другом. Комбинация — это подсчет выборок, которые мы делаем из n объектов. Принимая во внимание, что перестановка подсчитывает количество аранжировок из n объектов.

Мы должны помнить, что Комбинации делают акцент не на порядке, расположении или размещении, а на выборе.

Как учащиеся могут повторять перестановки и комбинации в Веданту?

Vedantu — это надежная онлайн-платформа для обучения студентов, которую могут использовать все студенты абсолютно бесплатно. В нем есть соответствующий материал о перестановках и комбинациях для изучения, если кто-то узнает о разнице между перестановками и комбинациями.

На этой странице описаны основы каждого из них, а затем описаны сходства и различия. Все расписано доходчиво и простым языком. Объяснено, как происходит подбор музыки, еды, одежды и других предметов быта.

Перестановки и комбинации — довольно интересная тема, которую необходимо решать стратегически.

Где учащиеся узнают о разнице между перестановками и комбинациями в Интернете?

Студенты могут найти то же самое на Веданту. Эта страница очень информативна с точки зрения объяснения перестановок и комбинаций. Эта глава имеет решающее значение в математике, и если учащиеся усвоят основы этой темы, они будут хорошо подготовлены к таким темам, как вероятность и статистика позже. Студентам просто нужно войти на портал Vedantu, чтобы получить к ним доступ.

Разница между перестановкой и комбинацией объясняется на примерах

8-минутное чтение

Перестановки и комбинации — это тема, полная загадок. Самый большой из них — понимание разницы между перестановкой и комбинацией. Должен ли я решить этот вопрос, используя перестановку или комбинацию? В этой статье мы дадим вам надежный метод, чтобы отличить их друг от друга. В последней статье цикла «Перестановки и комбинации» мы говорили о том, «когда складывать и умножать»?

Если вы не читали статью, вот ссылка: GMAT Permutation and Combination | Когда складывать и умножать

Следующая статья в этой серии — «Перестановка и комбинация» | Избегайте этих 3 ошибок | GMAT Quant

Имея общее представление о ключевых словах И – ИЛИ, давайте углубимся в углубленную концепцию разницы между перестановкой и комбинацией.

В этой статье мы обсудим

• Общий случай разницы между вопросами перестановки и комбинации
• Подход с использованием ключевых слов для определения комбинированных вопросов
• Подход с использованием ключевых слов для определения перестановочных вопросов
• Визуализируйте разницу между перестановочными и комбинированными вопросами без ключевых слов
• Наглядные вопросы для лучшего понимания
• Еда на вынос

Чтобы получить какие-либо стратегические советы по поступлению на GMAT или MBA, напишите нам по адресу [email protected]. Воспользуйтесь бесплатной пробной версией и получите неограниченный доступ к концептуальным файлам, онлайн-сессиям и практическим вопросам.

Общий случай

В большинстве вопросов о перестановке и комбинации мы приходим к точке, когда нам нужно выбрать или расположить несколько вещей, и многие студенты становятся жертвами той же ошибки, применяя выбор вместо расположения и наоборот.

Чтобы прояснить эту путаницу, давайте обсудим два простых случая:

1. Из 3 игроков, A, B и C, сколько парных команд может быть сформировано?
2. Из 3 букв А, В и С сколько двузначных слов можно составить?

Оба примера кажутся вам одинаковыми?

Ну примеры не те.

Этот простой пример ясно показывает, что понимание перестановки и комбинации может помочь решить, когда имеет значение расположение и когда важен выбор.

Подход с использованием ключевых слов для определения комбинированных вопросов

Давайте поймем концепцию комбинирования, решив примеры 1–9.0003

В – Сколько парных команд можно сформировать из 3 игроков А, В и С?

 Решение:

Из 3 игроков A, B и C команды из 2 игроков могут быть:

1. Команда AB
2. Команда AC
3. Команда БК

Таким образом, у нас может быть только 3 парные команды из 3 игроков.

Теперь вместо того, чтобы решать это вручную, давайте применим подход к решению этого вопроса с помощью ключевых слов.

Важные ключевые слова для определения комбинированного вопроса

Некоторые из важных ключевых слов:

• Выберите
• Выберите
• Выбор
• Комбинация

Всякий раз, когда вы читаете вопрос, ищите приведенные выше ключевые слова, поскольку это полезные индикаторы, которые ясно говорят нам, что вопрос является комбинированным.

Давайте посмотрим на применение приведенных выше ключевых слов в двух задачах GMAT на перестановку и комбинацию.

Q 1 – В обществе из 10 членов мы должны выбрать комитет из 4 членов. Как владелец общества, Джон уже является членом комитета. Сколькими способами можно сформировать комитет.

Решение

Обратите внимание на подчеркнутое ключевое слово «выбрать» в вопросе.

Таким образом, это комбинированный вопрос. А для выбора мы применяем формулу nC

r , чтобы получить ответ.

• Теперь в вопросе нас просят выбрать комитет из 4 членов из 10 членов и Джон уже входит в состав комитета
  • Таким образом, мы должны выбрать 3 члена из 9

• По заявке NC 9Формула 0317 r , мы можем выбрать 3 члена из 9 членов в 9c ₃ способами, которые
  

Теперь давайте решим немного сложный вопрос.

Q 2 –  Аналитик порекомендует комбинацию из 3 промышленных запасов, 2 транспортных запасов, и 2 коммунальных запасов. Если аналитик может выбрать из 5 промышленных, 4 транспортных и 3 коммунальных акций, сколько различных комбинаций из 7 акций возможно?

Решение

Обратите внимание на подчеркнутые ключевые слова «Выбрать» и «Комбинации»

Теперь мы можем легко определить, что это вопрос выбора, верно?

Аналитик должен сформировать другую комбинацию из 7 различных акций.

Вы можете себе представить, как он может это сделать?

Подход

• Ему нужно выбрать 3 производственных запаса из 5 производственных запасов И,
• Ему нужно выбрать 2 транспортных запаса из 4 транспортных запасов А,
• Ему нужно выбрать 2 акции коммунальных служб из 3 акций коммунальных служб.
  • Обратите внимание на ключевое слово «И», которое указывает, что все три вышеуказанных события должны произойти одновременно.
  • Таким образом,

Применяя формулу NC _r , мы можем написать:

• 3 промышленных запаса из 5 промышленных запасов могут быть выбраны в 5C ₃ = 10 способов
• 2 транспортных запаса из 4 транспортных запасов можно выбрать в 4C
  2 = 6 контактов
• 2 запаса коммунальных услуг из 3 запасов коммунальных услуг могут быть выбраны в 3C ₂ = 3 способа

Таким образом, всего способов выбрать 7 акций = 10 × 6 × 3 = 180 способов.

Выводы

1. Следите за важными ключевыми словами, такими как выбор, выбор, комбинация в основе вопроса.
2. Количество способов выбрать r вещей из n вещей = nCr.

Теперь посмотрим, как работает перестановка.

Подход с использованием ключевых слов для определения вопросов перестановки

Давайте поймем концепцию перестановки, решив пример 2-

Сколько двухбуквенных слов можно составить из трех букв A, B и C?

Solution

Слова из 2 букв, которые можно составить из 3 букв A, B и C:

• AB
• ВА
• АС
• КА
• г. до н.э.
г. до н.э.
• КБ

Таким образом, мы можем составить 6 разных слов.

Вы заметили, что в сочетании выбор A и B дает только 1 команду, то есть AB?

Однако выбор A и B дает 2 разных слова, то есть AB и BA. Это происходит потому, что порядок расположения слов имеет значение. Но при создании команд состав команды не меняется, говорим ли мы AB или BA.

Такое расположение известно как перестановка.

Вы заметили использование ключевого слова «расположение» в перестановке?

• Если нет, обратите внимание: расположение слов в вопросе подразумевает перестановку

Теперь вместо того, чтобы решать это вручную, давайте применим подход к решению этого вопроса с помощью ключевых слов.

Давайте посмотрим на некоторые часто используемые ключевые слова, которые подразумевают перестановочный вопрос.

Важные ключевые слова для определения комбинированного вопроса

Некоторые из важных ключевых слов:

• Договоренности
• Упорядоченные способы
• Уникальный

Следите за приведенными выше ключевыми словами в вопросе.

Всякий раз, когда вы получаете вопрос с тремя указанными выше ключевыми словами, это будет подразумевать перестановочный вопрос. Давайте решим 1 вопрос, чтобы понять применение ключевых слов.

В. Каждый сигнал, который может подать определенный корабль, состоит из 3 разных флагов, подвешенных вертикально в определенном порядке. Сколько уникальных сигналов можно получить, используя 4 разных флага?

 Solution

Посетите наш бесплатный семинар по количественной оценке, чтобы получить точную оценку своих текущих способностей к GMAT и путь к достижению целевых результатов по количественной оценке GMAT.

Вы можете сэкономить до 30+ часов времени на подготовку и повысить свой общий балл GMAT на 40+ баллов , следуя плану действий, предоставленному в конце семинара.

Выводы

1. Ищите важные сочетания ключевых слов, упорядоченные пути и уникальные, чтобы определить вопрос перестановки.
2. Количество способов составить r вещей из n вещей = nPr.
3. Вопрос о размещении также можно решить, выбрав сначала «r» вещей среди «n» вещей, а затем расположив все «r» вещей.

Визуализируйте разницу между вопросами перестановки и комбинации без ключевых слов

Иногда вы можете получить вопрос, который неявно использует применение перестановки и комбинации. Итак, как мы определяем, является ли вопрос вопросом комбинации или вопросом перестановки?

Давайте разберемся с этим на нескольких примерах:

Q1 – В определенной лиге 8 команд, и каждая команда играет с другими командами ровно один раз. Каково общее количество игр, сыгранных в лиге?

 

Решение

Этот вопрос не включает важные ключевые слова, тогда как мы должны решить этот вопрос?

• Когда мы не можем найти ни одного ключевого слова, чтобы определить, является ли вопрос типом комбинации или типом перестановки, нам нужно визуализировать информацию, предоставленную нам в основе вопроса.

Давайте визуализируем информацию, указанную в вопросе, и посмотрим, сможем ли мы определить ее тип.

Нам дано:

• В лиге 8 команд

Мы знаем, что в каждой игре участвуют две команды.

• Матч между командой A и командой B аналогичен матчу между командой B и командой A
• Таким образом, чтобы каждый матч состоялся, мы должны выбрать только 2 команды, и в этом случае расстановка не будет иметь значения

Вы заметили, что мы пришли к ключевому слову SELECT , тщательно анализируя предоставленную информацию и делая осмысленные выводы.

Теперь осталось найти количество способов выбрать 2 команды из 8 команд.  

• Следовательно, общее количество сыгранных игр = 8C ₂ = 28 матчей

Давайте теперь немного увеличим сложность и решим следующий вопрос.

Q2 – На заседании правления компании присутствуют 10 членов.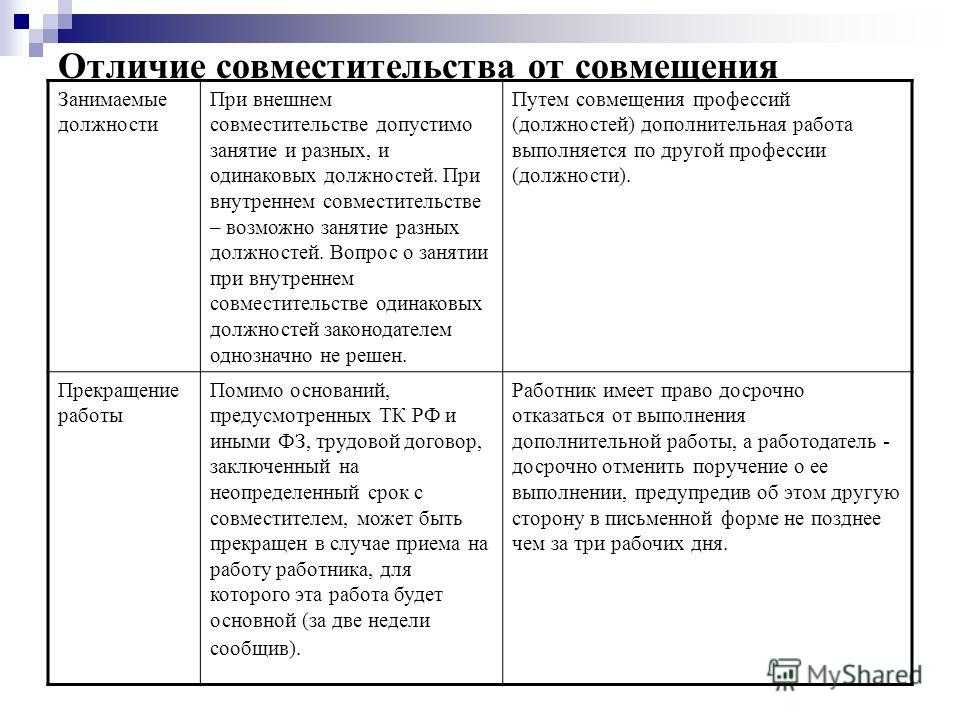 Каким образом 2 участника могут получить мандат на должность CEO и COO компании?

Решение

Мы не имеем никакого ключевого слова в вопросе, чтобы непосредственно определить тип вопроса и применить NC _R и NP _R Formula.

Таким образом, следующим шагом для решения такого типа вопросов является визуализация сценария, представленного в вопросе.

• Вопрос о получении мандата на должность CEO и COO компании
  • Предположим, что A и B являются двумя лидерами в голосовании и, следовательно, могут получить мандат на должность генерального директора или главного операционного директора.

• Теперь может быть 2 случая, в которых A и B могут получить мандат
  • A-> CEO и B-> COO
  • B-> CEO и A-> COO

Вы видите, что у нас есть 2 разных варианта выбора только 2 участников?

Таким образом, расстановка после выбора 2 членов предполагает перестановку.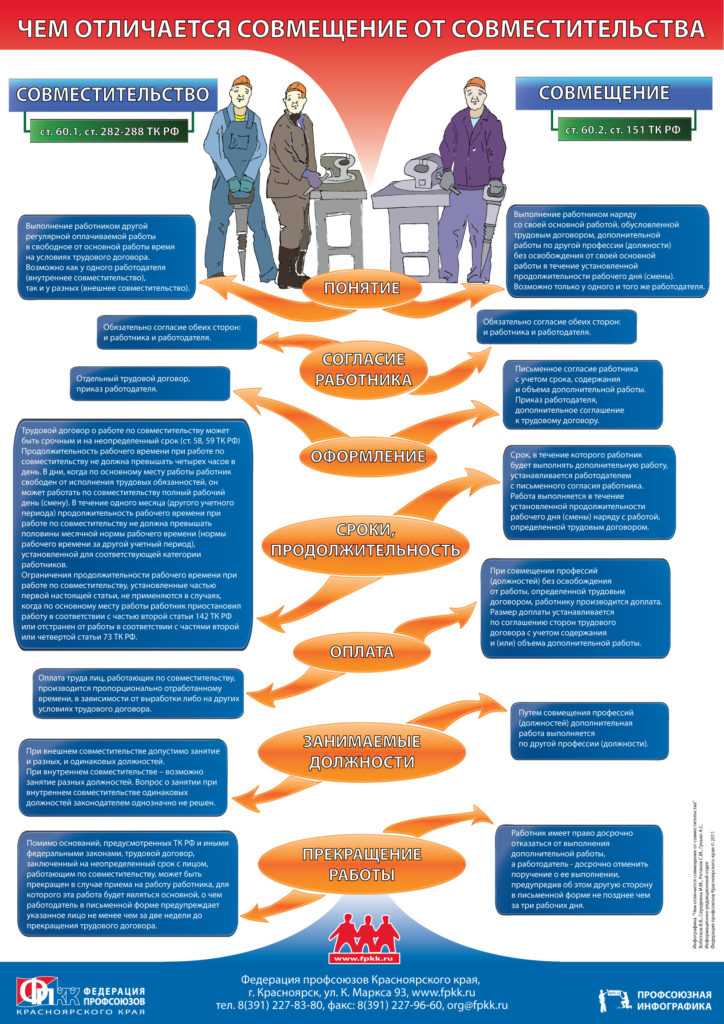

Таким образом, мы можем найти ответ 2 способами:

Способ 1:

Применяя формулу nP _r

• Количество способов, которыми 2 человека из 10 человек могут получить мандат на должность генерального директора и главного операционного директора компании = 1 0P ₂ = 90

Метод 2:

Сначала выбрав 2 элемента из 10 элементов, а затем расположив 2 элемента:

• Следовательно, общее количество способов = общее количество способов комбинирования 2 элементов × размещение 2 элементов
• Всего способов = 10C ₂ × r! = 45 × 2 = 90

Выводы

1. Всегда следите за ключевыми словами, использованными в вопросе. Ключевые слова могут помочь вам легко получить ответ.
2. Такие ключевые слова, как выбор, выбор, выбор и комбинация, указывают на то, что это комбинированный вопрос.
3. Ключевые слова как-расположение, упорядоченный, уникальный-указывает, что это вопрос перестановки.