Справка сзв м что это: СЗВ-М в 2022 году: сроки сдачи, заполнение, бланк новой формы и образец
Как заполнять СЗВ-М при увольнении сотрудника 2022
СЗВ-М работнику при увольнении — это один из обязательных документов, которые готовит и выдает работодатель. Но в этом случае есть нюансы заполнения.
Содержание
Отмена формы СЗВ-М с 2023 года
С 1 января 2023 года ПФР и ФСС объединили в единый Соцфонд. Это повлекло изменения по отчетности. Сразу пять отчетных форм (СЗВ-М, СЗВ-СТАЖ, СЗВ-ТД, ДСВ-3 и 4-ФСС) заменили одним отчетом ЕФС-1.
По форме СЗВ-М последний раз отчитываемся за декабрь 2022 года в срок до 16.01.2023. После этого СЗВ-М сдавать не нужно. Данные подавайте в составе ЕФС-1.
Подробнее: как заполнить и сдать новый отчет ЕФС-1
Зачем выдавать при увольнении
Сведения о застрахованных входящие, или, сокращенно, СЗВ-М, при увольнении сотрудника работодатель обязан выдать — это предписывает абзац 3 части 4 статьи 11 Федерального закона от 01.04.1996 № 27-ФЗ «Об индивидуальном (персонифицированном) учете в системе обязательного пенсионного страхования». Данное требование распространяется как на работников, заключивших трудовой договор, так и на тех, кто трудился по гражданско-правовым договорам.
Данное требование распространяется как на работников, заключивших трудовой договор, так и на тех, кто трудился по гражданско-правовым договорам.
Подробнее о документах, которые выдаются при увольнении
Как заполнить СЗВ-М, если сотрудник увольняется
Бланк заполняется, как правило, автоматически, с использованием программных средств, и представляет собой копию выписки из отчета, который работодатель ежемесячно направляет в ПФР. Но если под рукой не окажется нужной программы, то для начала необходимо взять форму отчета.
Шаг 1. Заполняем сведения о работодателе
Здесь просто указываем уставные реквизиты организации и переходим к заполнению оставшихся граф СЗВ-М на уволенных.
Шаг 2. Указываем период
Пишем месяц и год, в котором человек увольняется.
Шаг 3. Пишем тип формы
При увольнении ставим код “исход” — в смысле, документ исходящий.
Шаг 4. Заполняем сведения о работнике
Здесь пишем персональные данные увольняющегося человека.
Шаг 5. Подписываем и отдаем работнику
Так выглядит СЗВ-М, если работник уволился. Печать на документ ставится при её наличии. Если печати нет — значит, и ставить ничего не надо, это не является нарушением.
Включаются ли в СЗВ-М уволенные сотрудники
При выдаче копии увольняемому на руки
Данная форма персонифицирована, то есть при прекращении трудовых отношений документ выдается уходящему персонально. Включать других людей сюда не надо, потому что эти сведения относятся к персональным данным и охраняются законом.
Кроме того, в соответствии с законодательством работодатель должен не только выдать этот документ, но и получить документальное свидетельство, что СЗВ-М был выдан человеку.
При предоставлении отчета
Как показать уволенных в СЗВ-М при предоставлении отчетов, заботит многих.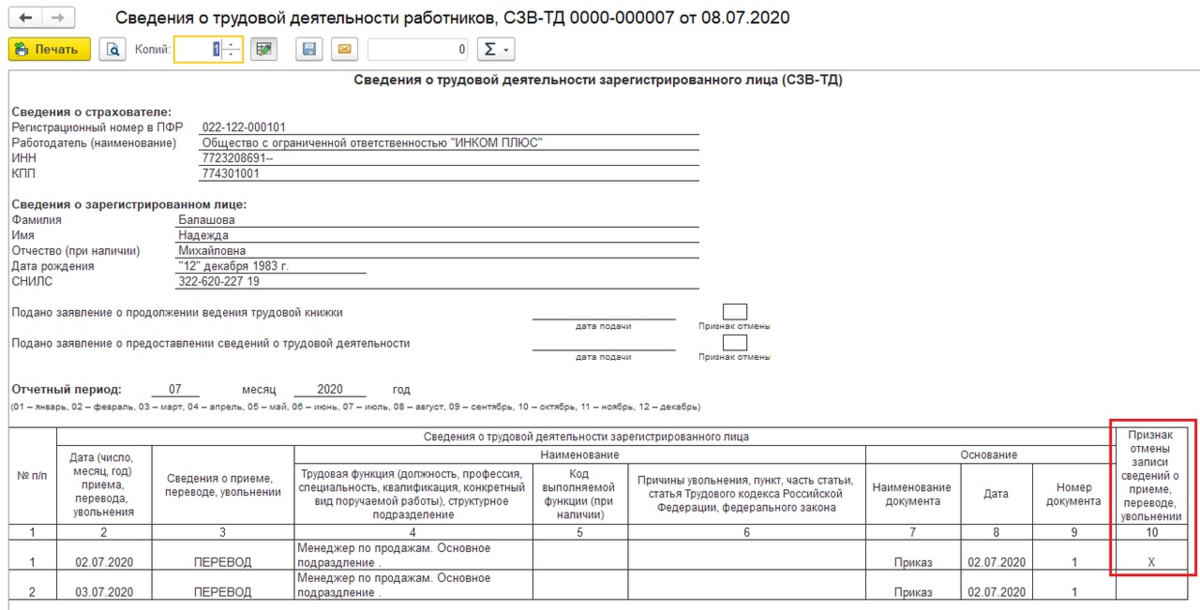 При сдаче отчета в ПФР за отчетный период в нем указываются все работники, в том числе и уволенные. В дальнейшем сведения об уволенных исключаются, но если человек уволился первого апреля, то при подаче отчета за апрель сведения о нем должны быть в форме СЗВ-М.
При сдаче отчета в ПФР за отчетный период в нем указываются все работники, в том числе и уволенные. В дальнейшем сведения об уволенных исключаются, но если человек уволился первого апреля, то при подаче отчета за апрель сведения о нем должны быть в форме СЗВ-М.
Документы, которые нужно выдать работнику при увольнении в 2023 году
Вера Ревина/Клерк.руВ 2023 году увольняющимся работникам нужно выдать такой же «большой» пакет документов, как и раньше, но по новым формам. Форму 182н теперь выдавать не нужно, ее отменили.
А справку о заработке и НДФЛ, которую все привычно называют 2-НДФЛ, нужно выдавать по запросу работника. Она и раньше не входила в список обязательных документов, но все бухгалтеры старались ее выдать.
В 2023 году, если работники не просят 2-НДФЛ, справку можно не выдавать. При необходимости все ее могут получить на сайте ФНС через свои личные кабинеты.
Но есть и другие нюансы, которые нужно знать кадровикам. Мы о них рассказываем на курсе профпереподготовки «Кадровик с нуля до профи».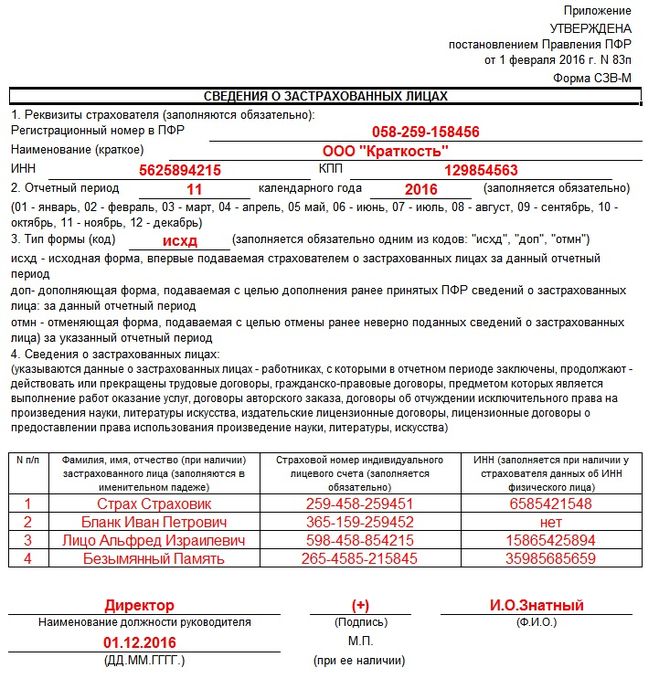 Приходите — научим.
Приходите — научим.
Список документов, которые нужно выдать работнику при увольнении:
Бумажная трудовая книжка или сведения о трудовой деятельности по форме СТД-Р.
Выписка из раздела 3 РСВ «Персонифицированные сведения о застрахованных лицах» (год).
Выписка из ЕФС-1. Подраздел 1.2 Сведения о страховом стаже (бывшая СЗВ-СТАЖ).
Выписка из персонифицированных сведений о физлицах (вместо СЗВ-М).
Расчетный листок.
Оригиналы документов, если они были сданы в кадровую службу.
Другие документы, среди которых «Справка о доходах физического лица» (ранее форма 2-НДФЛ), копии приказа о приеме на работу и увольнении и т.п., нужно выдать, только в то случае, если работник напишет заявление с просьбой получить эти документы.
Какие документы выдавать при увольнении в 2023 году: сравнительная таблица с комментариями
Какие документы выдавали в 2022 году | Какие документы должны выдавать в 2023 году | Документ, которым утверждена форма 2023 года | Что изменилось |
Обязательно | |||
Бумажная трудовая книжка тем, кто сохранил бумажный вариант | Бумажная трудовая книжка работникам, которые сохраняют бумажные вариант книжки | По имеющейся форме (по факту). | Без изменений |
Форма СТД-Р тем, кто перешел на электронный формат трудовой | Форма СТД-Р тем, кто перешел на электронный формат трудовой | Утверждена в Приложении № 1 к приказу Минтруда от 10 ноября 2022 г. № 713н | Без изменений |
Выписка из раздела 3 РСВ «Персонифицированные сведения о застрахованных лицах» (год) | Выписка из раздела 3 РСВ «Персонифицированные сведения о застрахованных лицах» (год) | Утверждена приказом ФНС от 29 сентября 2022 г. №ЕД-7-11/878@ | С 2023 года применяется новая форма |
Выписка из СЗВ-СТАЖ (год) | Выписка из ЕФС-1. | ЕФС-1 утверждена постановлением Правления ПФ РФ от 31 октября 2022 г. № 245п. | Форма СЗВ-СТАЖ была отдельной, с 2023 года вошла в единую форму ЕФС-1. По сути, не изменилась |
Выписка из СЗВ-М (последний месяц) | Выписка из персонифицированных сведений о физлицах | Утверждена Приказом ФНС России от 29.09.2022 № ЕД-7-11/878@ в приложении № 2. | Форма утверждена заново. |
Оригиналы документов, если они были сданы в кадровую службу | Оригиналы документов, если они были сданы в кадровую службу | Разные. | Без изменений |
Расчетный листок | Расчетный листок за последний месяц (или отработанные период месяца) | По форме, утвержденной и применяемой в компании | Без изменений |
Справка о заработке за 2 года по форме 182н |
|
| Отменена с 2023 года |
Справка о доходах физического лица (ранее форма 2-НДФЛ), с 2022 года вошла в состав 6-НДФЛ) примеч. См. раздел по запросу работника |
|
| Выдается по запросу |
По запросу работника | |||
| Справка о доходах работника и НДФЛ по форме приложения 1 к расчету 6-НДФЛ (бывшая 2-НДФЛ) | Утверждена в составе 6-НДФЛ Приказом ФНС России от 29 сентября 2022 г. | Выдавалась обязательно |
Справка о среднем заработке для службы занятости | Справка о среднем заработке для службы занятости | Форму справки утверждают региональные центры занятости. Для Москвы: Приложение 1 к приказу ДТСЗН города Москвы от 24 декабря 2018 года № 1721 | Без изменений |
Приказы о приеме, увольнении, награждении, переводах | Приказы о приеме, увольнении, награждении, переводах | По формам, применяемым в организации | Без изменений |
Дополнительно | |||
Выписка из формы ДСВ-3 за квартал увольнения, перечисляли взносы на накопительную часть пенсии | Выписка из ЕФС-1. | ЕФС-1 утверждена постановлением Правления ПФ РФ от 31 октября 2022 г. № 245п. | Форма ДСВ-3 вошла состав единой отчетной формы ЕФС-1, которая сдается в Соцфонд России |
Документы, которые выдаются работнику при увольнении
Трудовая книжка или Сведения о трудовой деятельности по форме СТД-Р
Трудовую книжку нужно выдать работнику на руки «под роспись» в последний день работы.
Если работник уходит в отпуск с последующим увольнением книжку выдают в последний рабочий день перед отпуском.
Если работник отказался от печатного варианта трудовой книжки и перешел на электронный формат, ему выдают«Сведения о трудовой деятельности по форме СТД-Р». Действующая в 2023 году форма утверждена приказом Минтруда от 10 ноября 2022 г. № 713н в Приложении № 1.
№ 713н в Приложении № 1.
Обычно трудовую книжки выдают на руки. Но работник может написать заявление и подучить ее по почте в бумажном формате или по электронной почте – по форме СТД (ч. 5 ст. 66.1 ТК).
Выписка из Раздела 3 формы Расчета по страховым взносам (РСВ)
С 1 января 2023 года ответ по форме РСВ изменен в связи с объединением ПФР и ФСС в единый Соцфонд. Форма утверждена приказом ФНС от 29 сентября 2022 г. № ЕД-7-11/878@.
Выдавать выписку нужно не только уволившимся сотрудникам компании, и работникам, с которыми расторгли договор гражданско-правового характера на выполнение работ и оказание услуг.
Выписка из формы ЕФС-1
С 2023 года формы СЗВ-СТАЖ, ДСВ-3 вошли в состав единой отчетной формыЕФС-1, которую сдают в Соцфонд. Она утверждена утверждена постановлением Правления ПФ от 31 октября 2022 г. № 245п.
Увольняющему работнику нужно сделать выписку из подраздел 1.2 «Сведения о страховом стаже» раздела 1 «Сведения о трудовой (иной) деятельности, страховом стаже, заработной плате и дополнительных страховых взносах на накопительную пенсию». Этот подраздел заменяет бывшую форму СЗВ-СТАЖ.
Этот подраздел заменяет бывшую форму СЗВ-СТАЖ.
Обратите внимание, с 2023 года выписку из ЕФС-1 нужно выдавать не только работникам, которые работали по трудовым договорам, но и тем, с кем расторгнут гражданско-правовой договор.
Выписка из отчета «Персонифицированные сведения о физлицах»
Отчет «Персонифицированные сведения о физлицах» заменил ранее действующую СЗВ-М.
В нем указывают персональные данные работников и сведения о суммах выплат и иных вознаграждений в их пользу. Форма утверждена Приказом ФНС от 29.09.2022 № ЕД-7-11/878@ в приложении № 2.
Расчетный листок
Расчетный листок должен выдаваться работнику при каждой выплате заработной платы, в том числе и при увольнении с учетом сумм, выплаченных увольняющемуся.
Кроме того, работнику нужно вернуть оригиналы документов, если он какие-либо сдавал при приеме на работу. Это могут справки об отсутствии судимости, медсправки, медкнижка, диплом и т.п.
Выписка из ЕФС-1 подраздел 3
Это бывшая ДСВ-3, которая с 2023 года вошла в состав ЕФС-1, как Подраздел 3 «Сведения о застрахованных лицах, за которых перечислены дополнительные страховые взносы на накопительную пенсию и уплачены взносы работодателя».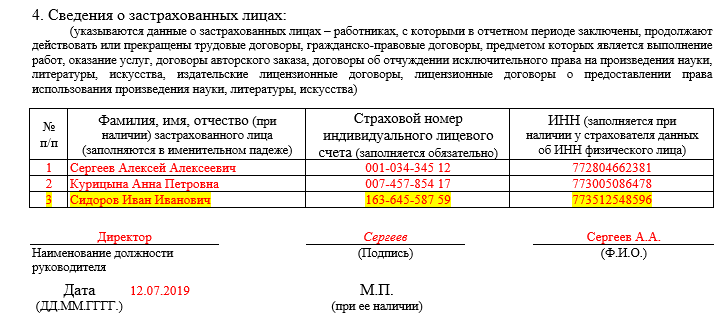
ЕФС-1 утверждена постановлением Правления ПФР от 31 октября 2022 г. № 245п.
Выписку выдают компании, которые платят за работника дополнительные взносы на накопительную пенсию.
Выписку нужно сделать за квартал увольнения, с указанием в нем перечисленных взносов на накопительную часть пенсии.
Документы, которые выдаются работнику по заявлению
Если работнику нужны какие-либо документы кроме тех, которые он получил при увольнении в качестве обязательных, он вправе письменнозапросить другие документы, связанные в работой.
Выяснять у работника, зачем они ему нужны, не нужно. Это будет считаться нарушением ТК.
Перечень документов, которые может запросить работников открытый. Это могут быть заверенные копии кадровых приказов о приеме и увольнении, переводах, повышении квалификации и т.п.
Выдать документы по запросу работника нужно в течение трех рабочих дней (ст. 62 ТК).
Справка 2-НДФЛ
Пунктом 3 статьи 230 НК установлено, что справка о доходах и удержаниях из них выдается по требованию работника.
Она больше не называется 2-НДФЛ, это просто справка о доходах и суммах налога физического лица. Справка вошла в состав формы 6-НДФЛ.
С 1 квартала 2023 года Приказ ФНС России от 29.09.2022 № ЕД-7-11/881@ введена новая форма 6-НДФЛ. Но приложение со справкой перенесено в новый приках без изменений.
Справка о среднем заработке для службы занятости
Эта справка может понадобится работнику, который намерен зарегистрироваться в
Единой формы справки нет. Каждый региональный ЦЗ утверждает свою формую.
Метод опорных векторов (SVM) Объяснение алгоритма
Итак, вы работаете над задачей классификации текста. Вы уточняете свои тренировочные данные и, возможно, даже экспериментировали с Наивным Байесом. Вы уверены в своем наборе данных и хотите сделать еще один шаг вперед.
Введите Метод опорных векторов (SVM) , быстрый и надежный алгоритм классификации, который очень хорошо работает с ограниченным объемом данных для анализа.
Возможно, вы копнули глубже и наткнулись на такие термины, как линейно разделяемые , хитрость ядра и функции ядра . Но не бойтесь! Идея, лежащая в основе алгоритма SVM, проста, и его применение в NLP не требует большинства сложных вещей.
В этом руководстве вы узнаете об основах SVM и о том, как использовать его для классификации текста. Наконец, вы увидите, как легко начать работу с таким инструментом, не требующим написания кода, как MonkeyLearn.
Начните классифицировать текст с помощью SVM
ПОПРОБУЙТЕ СЕЙЧАС
- Что такое машины опорных векторов?
- Как работает SVM?
- Использование SVM с классификацией естественного языка
- Учебное пособие по простому классификатору SVM
Что такое машины опорных векторов?
Машина опорных векторов (SVM) — это контролируемая модель машинного обучения, которая использует алгоритмы классификации для задач классификации с двумя группами. Предоставив модели SVM наборы помеченных обучающих данных для каждой категории, они могут классифицировать новый текст.
Предоставив модели SVM наборы помеченных обучающих данных для каждой категории, они могут классифицировать новый текст.
По сравнению с более новыми алгоритмами, такими как нейронные сети, у них есть два основных преимущества: более высокая скорость и лучшая производительность при ограниченном количестве выборок (в тысячах). Это делает алгоритм очень подходящим для задач классификации текста, где обычно имеется доступ к набору данных, состоящему не более чем из пары тысяч помеченных образцов.
Как работает SVM?
Основы работы с методами опорных векторов и принцип их работы лучше всего понять на простом примере. Представим, что у нас есть два тега: красный и синий , и наши данные имеют две особенности: x и y . Нам нужен классификатор, который, учитывая пару координат (x,y) , выводит, если это либо красный , либо синий . Мы наносим наши уже размеченные данные обучения на плоскость:
Наши размеченные данные
Машина опорных векторов берет эти точки данных и выводит гиперплоскость (которая в двух измерениях представляет собой просто линию), которая лучше всего разделяет теги. Эта линия граница решения : все , что попадает в одну сторону от нее , мы будем классифицировать как синий , а все , что попадает в другую , как красный .
Эта линия граница решения : все , что попадает в одну сторону от нее , мы будем классифицировать как синий , а все , что попадает в другую , как красный .
В 2D лучшая гиперплоскость — это просто линия
Но что такое лучшая гиперплоскость ? Для SVM это тот, который максимизирует поля от обоих тегов. Другими словами: гиперплоскость (помните, что в данном случае это линия), чье расстояние до ближайшего элемента каждого тега является наибольшим.
Не все гиперплоскости созданы равными
Вы можете посмотреть этот видеоурок, чтобы узнать, как именно находится эта оптимальная гиперплоскость.
Нелинейные данные
Теперь этот пример был простым, поскольку ясно, что данные линейно разделимы — мы могли провести прямую линию, чтобы разделить красных и синих . К сожалению, обычно все не так просто. Взгляните на этот случай:
Более сложный набор данных
Совершенно очевидно, что здесь нет линейной границы решения (одна прямая линия, разделяющая оба тега). Однако векторы очень четко разделены, и кажется, что их должно быть легко разделить.
Однако векторы очень четко разделены, и кажется, что их должно быть легко разделить.
Вот что мы сделаем: мы добавим третье измерение. До сих пор у нас было два измерения: x и y . Создаем новый размер z и правим, чтобы он вычислялся определенным удобным для нас способом: z = x² + y² (заметьте, это уравнение для окружности).
Это даст нам трехмерное пространство. Срез этого пространства выглядит так:
С другой точки зрения, данные теперь разделены на две линейно разделенные группы
Что может сделать с этим SVM? Посмотрим:
Отлично! Обратите внимание, что поскольку мы сейчас находимся в трех измерениях, гиперплоскость представляет собой плоскость, параллельную оси x на определенном расстоянии z (скажем, z = 1 ).
Осталось отобразить его обратно в два измерения:
Вернуться к нашему исходному виду, теперь все аккуратно разделено
И вот мы идем! Наша граница решения — это окружность радиусом 1, которая разделяет обе метки с помощью SVM. Посмотрите эту 3D-визуализацию, чтобы увидеть еще один пример того же эффекта:
Посмотрите эту 3D-визуализацию, чтобы увидеть еще один пример того же эффекта:
Хитрость ядра
В нашем примере мы нашли способ классифицировать нелинейные данные, умело отображая наше пространство в более высокое измерение. Однако оказывается, что вычисление этого преобразования может стать довольно затратным с точки зрения вычислений: может быть много новых измерений, каждое из которых, возможно, требует сложных вычислений. Выполнение этого для каждого вектора в наборе данных может потребовать много работы, поэтому было бы здорово, если бы мы могли найти более дешевое решение.
И нам повезло! Вот хитрость: SVM не нужны настоящие векторы, чтобы творить чудеса, на самом деле он может обойтись только скалярными произведениями между ними. Это означает, что мы можем избежать дорогостоящих расчетов новых измерений.
Вместо этого мы делаем следующее:
Представьте себе новое пространство, которое нам нужно:
z = x² + y²
Выясните, что точечный продукт в этом пространстве выглядит так:
a · b = xa · xb + ya · yb + za · zb
a · b = xa · xb + ya · yb + (xa² + ya²) · (xb² + yb²) 9 0006
Прикажите SVM сделать свое дело, но с использованием нового скалярного произведения — мы называем это функция ядра .

Вот и все! Это трюк ядра , который позволяет нам обойти множество дорогостоящих вычислений. Обычно ядро линейно, и мы получаем линейный классификатор. Однако, используя нелинейное ядро (как указано выше), мы можем получить нелинейный классификатор, вообще не преобразовывая данные: мы только меняем скалярное произведение на нужное нам пространство, и SVM будет счастливо пыхтеть.
Обратите внимание, что трюк с ядром на самом деле не является частью SVM. Его можно использовать с другими линейными классификаторами, такими как логистическая регрессия. Машина опорных векторов занимается только поиском границы решения.
Использование SVM с классификацией естественного языка
Итак, мы можем классифицировать векторы в многомерном пространстве. Большой! Теперь мы хотим применить этот алгоритм для классификации текста, и первое, что нам нужно, — это способ преобразовать фрагмент текста в вектор чисел, чтобы мы могли запускать с ними SVM. Другими словами, какие функций мы должны использовать, чтобы классифицировать тексты с помощью SVM?
Другими словами, какие функций мы должны использовать, чтобы классифицировать тексты с помощью SVM?
Самый распространенный ответ — частоты слов, как мы это делали в Наивном Байесе. Это означает, что мы относимся к тексту как к набору слов, и для каждого слова, появляющегося в этом наборе, у нас есть характеристика. Значение этой функции будет зависеть от того, насколько часто это слово встречается в тексте.
Этот метод сводится к тому, чтобы просто подсчитать, сколько раз каждое слово встречается в тексте, и разделить его на общее количество слов. Так, в предложении «Все обезьяны — приматы, но не все приматы — обезьяны» слово обезьян имеет частоту 2/10 = 0,2, а слово , но имеет частоту 1/10 = 0,1.
Для более продвинутой альтернативы расчета частот мы также можем использовать TF-IDF.
Теперь, когда мы это сделали, каждый текст в нашем наборе данных представлен в виде вектора с тысячами (или десятками тысяч) измерений, каждое из которых представляет частоту одного из слов текста. Идеальный! Это то, что мы скармливаем SVM для обучения. Мы можем улучшить это, используя методы предварительной обработки, такие как выделение корней, удаление стоп-слов и использование n-грамм.
Идеальный! Это то, что мы скармливаем SVM для обучения. Мы можем улучшить это, используя методы предварительной обработки, такие как выделение корней, удаление стоп-слов и использование n-грамм.
Выбор функции ядра
Теперь, когда у нас есть векторы признаков, осталось только выбрать функцию ядра для нашей модели. Каждая проблема уникальна, и работа ядра зависит от того, как выглядят данные. В нашем примере наши данные были расположены концентрическими кругами, поэтому мы выбрали ядро, которое соответствовало этим точкам данных.
Принимая это во внимание, что лучше всего подходит для обработки естественного языка? Нужен ли нам нелинейный классификатор? Или данные линейно разделимы? Оказывается, лучше всего придерживаться линейного ядра. Почему?
В нашем примере у нас было две функции. Некоторые реальные применения SVM в других областях могут использовать десятки или даже сотни функций. Между тем, классификаторы НЛП используют тысяч признаков, поскольку они могут иметь до одного на каждое слово, которое появляется в обучающих данных. Это немного меняет проблему: хотя использование нелинейных ядер может быть хорошей идеей в других случаях, наличие такого количества функций в конечном итоге приведет к тому, что нелинейные ядра перекроют данные. Поэтому лучше просто придерживаться старого доброго линейного ядра, которое на самом деле дает наилучшую производительность в этих случаях.
Это немного меняет проблему: хотя использование нелинейных ядер может быть хорошей идеей в других случаях, наличие такого количества функций в конечном итоге приведет к тому, что нелинейные ядра перекроют данные. Поэтому лучше просто придерживаться старого доброго линейного ядра, которое на самом деле дает наилучшую производительность в этих случаях.
Собираем все вместе
Осталось только потренироваться! Мы должны взять наш набор помеченных текстов, преобразовать их в векторы, используя частоты слов, и передать их алгоритму, который будет использовать выбранную нами функцию ядра, чтобы он создал модель. Затем, когда у нас есть новый неразмеченный текст, который мы хотим классифицировать, мы конвертируем его в вектор и передаем модели, которая выведет тег текста.
Учебное пособие по простому классификатору SVM
Чтобы создать собственный классификатор SVM, не заморачиваясь с векторами, ядрами и TF-IDF, вы можете сразу же приступить к работе с одной из предварительно созданных моделей классификации MonkeyLearn. Кроме того, легко создавать свои собственные благодаря интуитивно понятному пользовательскому интерфейсу платформы и подходу без кода.
Кроме того, легко создавать свои собственные благодаря интуитивно понятному пользовательскому интерфейсу платформы и подходу без кода.
Это также отлично подходит для тех, кто не хочет вкладывать большие суммы капитала в найм экспертов по машинному обучению.
Давайте покажем вам, как легко создать классификатор SVM за 8 простых шагов. Прежде чем начать, вам необходимо бесплатно зарегистрироваться в MonkeyLearn.
1. Создайте новый классификатор
Перейдите на панель инструментов, нажмите «Создать модель» и выберите «Классификатор».
2. Выберите, как вы хотите классифицировать данные
Мы собираемся выбрать модель «Тематическая классификация» для классификации текста на основе темы, аспекта или релевантности.
3. Импорт данных обучения
Выберите и загрузите данные, которые вы будете использовать для обучения модели. Имейте в виду, что классификаторы учатся и становятся умнее, когда вы предоставляете им больше обучающих данных. Вы можете импортировать данные из файлов CSV или Excel.
Вы можете импортировать данные из файлов CSV или Excel.
4. Определите теги для вашего классификатора SVM
Пришло время определить ваши теги, которые вы будете использовать для обучения вашего классификатора тем. Добавьте как минимум два тега для начала — вы всегда можете добавить больше тегов позже.
5. Отметьте данные для обучения вашего классификатора
Начните обучение вашего классификатора тем, выбрав теги для каждого примера:
После ручной пометки некоторых примеров классификатор начнет делать прогнозы самостоятельно. Если вы хотите, чтобы ваша модель была более точной, вам придется пометить больше примеров, чтобы продолжить обучение модели.
Чем больше данных вы пометите, тем умнее будет ваша модель.
6. Установите алгоритм SVM
Перейдите в настройки и убедитесь, что вы выбрали алгоритм SVM в расширенном разделе.
7. Протестируйте свой классификатор
Теперь вы можете протестировать свой классификатор SVM, нажав «Выполнить» > «Демо». Напишите свой собственный текст и посмотрите, как ваша модель классифицирует новые данные:
Напишите свой собственный текст и посмотрите, как ваша модель классифицирует новые данные:
8. Интегрируйте классификатор тем
Вы научили свою модель делать точные прогнозы при классификации текста. Теперь пришло время загрузить новые данные! В MonkeyLearn это можно сделать тремя различными способами:
Пакетная обработка: перейдите в «Выполнить» > «Пакетная обработка» и загрузите файл CSV или Excel. Классификатор проанализирует ваши данные и отправит вам новый файл с прогнозами.
API: используйте MonkeyLearn API для классификации новых данных из любого места.
Интеграции: подключайте повседневные приложения для автоматического импорта новых текстовых данных в ваш классификатор. Такие интеграции, как Google Sheets, Zapier и Zendesk, можно использовать, не вводя ни одной строки кода:
Заключительные слова
И это основы работы с методами опорных векторов!
Подводя итог:
- Метод опорных векторов позволяет классифицировать данные, которые являются линейно разделимыми.

- Если это не линейно разделимо, вы можете использовать трюк с ядром, чтобы заставить его работать.
- Однако для текстовой классификации лучше придерживаться линейного ядра.
С помощью инструментов MLaaS, таких как MonkeyLearn, очень просто внедрить SVM для классификации текста и сразу же получить ценную информацию.
Есть вопросы? Запланируйте демонстрацию, и мы поможем вам начать работу.
Полное руководство для начинающих
Эта статья была опубликована в рамках блога Data Science Blogathon
Введение в метод опорных векторов (SVM)
SVM — это мощный контролируемый алгоритм, который лучше всего работает с небольшими наборами данных, но со сложными. Машина опорных векторов, сокращенно SVM, может использоваться как для задач регрессии, так и для задач классификации, но, как правило, они лучше всего работают в задачах классификации. Они были очень известны в то время, когда они были созданы, в 1990-х годах, и продолжают оставаться популярным методом для высокопроизводительного алгоритма с небольшой настройкой.
Надеюсь, вы уже освоили деревья решений, случайный лес, наивный байесовский метод, метод K-ближайшего соседа и ансамблевое моделирование. Если нет, я бы посоветовал вам уделить несколько минут и прочитать о них.
В этой статье я объясню вам, что такое SVM, как работает SVM, а также математическую интуицию, лежащую в основе этого важного алгоритма машинного обучения.
Содержание- Что такое метод опорных векторов?
- Когда использовать логистическую регрессию против SVM?
- Типы SVM
- Как работает SVM
- Математическая интуиция за SVM
- Скалярное произведение
- Использование скалярного произведения в SVM
- Маржа
- Функция оптимизации и ее ограничения
- Мягкая маржа SVM
- Ядра SVM
- Различные типы ядер
- Как правильно выбрать ядро в SVM
- Реализация и настройка гиперпараметров SVM в Python
- Преимущества и недостатки SVM
- Конечные примечания
Это задача машинного обучения с учителем, в которой мы пытаемся найти гиперплоскость, которая лучше всего разделяет два класса.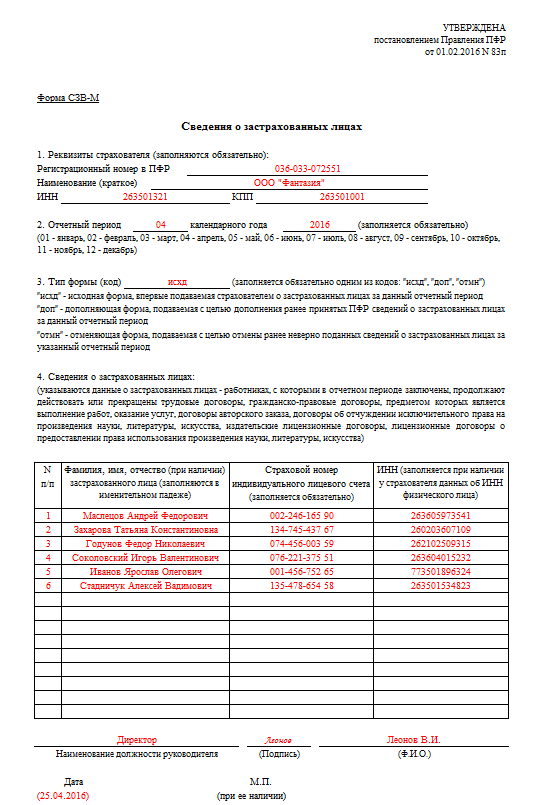
Теперь вопрос в том, какую гиперплоскость он выбирает? Может быть бесконечное количество гиперплоскостей, проходящих через точку и идеально классифицирующих два класса. Итак, какой из них лучший?
Итак, SVM делает это, находя максимальное расстояние между гиперплоскостями, что означает максимальное расстояние между двумя классами.
Когда использовать логистическую регрессию и метод опорных векторов?
В зависимости от количества имеющихся у вас функций вы можете выбрать логистическую регрессию или SVM.
SVM лучше всего работает, когда набор данных небольшой и сложный. Обычно рекомендуется сначала использовать логистическую регрессию и посмотреть, как она работает, если она не дает хорошей точности, вы можете использовать SVM без какого-либо ядра (подробнее о ядрах мы поговорим в следующем разделе).
Только когда данные идеально линейно разделимы, мы можем использовать Linear SVM. Идеальная линейная разделимость означает, что точки данных можно разделить на 2 класса, используя одну прямую линию (если она двумерная).
Нелинейный SVMКогда данные не являются линейно разделимыми, мы можем использовать нелинейный SVM, что означает, что когда точки данных не могут быть разделены на 2 класса с помощью прямой линии (если они 2D), тогда мы используем некоторые передовые методы, такие как приемы ядра, для их классификации. . В большинстве реальных приложений мы не находим линейно разделяемых точек данных, поэтому для их решения мы используем трюк ядра.
Теперь давайте определим два основных термина, которые будут неоднократно повторяться в этой статье:
Опорные векторы: Это точки, которые находятся ближе всего к гиперплоскости. Разделительная линия будет определена с помощью этих точек данных.
Разделительная линия будет определена с помощью этих точек данных.
Поле: это расстояние между гиперплоскостью и ближайшими к гиперплоскости наблюдениями (опорными векторами). В SVM большая маржа считается хорошей маржой. Существует два типа полей жесткие поля и мягкие поля. Подробнее об этих двух я расскажу в следующем разделе.
Изображение 1
Как работает машина опорных векторов? SVM определяется таким образом, что он определяется только в терминах опорных векторов, нам не нужно беспокоиться о других наблюдениях, поскольку запас делается с использованием точек, которые находятся ближе всего к гиперплоскости (опорные векторы), тогда как в логистической регрессии классификатор определен по всем точкам. Следовательно, SVM обладает некоторыми естественными ускорениями.Давайте разберемся с работой SVM на примере. Предположим, у нас есть набор данных с двумя классами (зеленый и синий). Мы хотим классифицировать эту новую точку данных как синюю или зеленую.

Источник изображения: Автор
Чтобы классифицировать эти точки, у нас может быть много границ решений, но вопрос в том, какая из них наилучшая и как ее найти? ПРИМЕЧАНИЕ: Поскольку мы наносим точки данных на двумерный график, мы называем эту границу решения прямой линией
Лучшей гиперплоскостью является та плоскость, которая максимально удалена от обоих классов, и это основная цель SVM. Это делается путем поиска различных гиперплоскостей, которые наилучшим образом классифицируют метки, после чего выбирается та, которая находится дальше всего от точек данных, или та, которая имеет максимальный запас.
Источник изображения: Автор Математическая интуиция за машиной опорных векторов Многие люди игнорируют математическую интуицию, стоящую за этим алгоритмом, потому что его довольно сложно переварить. Здесь, в этом разделе, мы постараемся понять каждый шаг работы под капотом. SVM — это широкая тема, и люди все еще проводят исследования этого алгоритма. Если вы планируете проводить исследования, то это может быть неподходящим местом для вас.
Здесь, в этом разделе, мы постараемся понять каждый шаг работы под капотом. SVM — это широкая тема, и люди все еще проводят исследования этого алгоритма. Если вы планируете проводить исследования, то это может быть неподходящим местом для вас.
Здесь мы поймем только ту часть, которая требуется при реализации этого алгоритма. Вы, должно быть, слышали о основная формулировка, двойная формулировка, множитель Лагранжа и т. д. Я не говорю, что эти темы не важны, но они более важны, если вы планируете проводить исследования в этой области. Давайте двигаться вперед и увидеть магию этого алгоритма.
Прежде чем углубляться в мельчайшие подробности этой темы, давайте сначала разберемся, что такое точечный продукт.
Все мы знаем, что вектор — это величина, которая имеет не только направление, но и величину, и точно так же, как числа, мы можем использовать математические операции, такие как сложение, умножение. В этом разделе мы попытаемся узнать об умножении векторов, которое можно выполнить двумя способами: скалярным произведением и перекрестным произведением. Разница только в том, что скалярное произведение используется для получения в результате скалярного значения, тогда как перекрестное произведение используется для повторного получения вектора.
В этом разделе мы попытаемся узнать об умножении векторов, которое можно выполнить двумя способами: скалярным произведением и перекрестным произведением. Разница только в том, что скалярное произведение используется для получения в результате скалярного значения, тогда как перекрестное произведение используется для повторного получения вектора.
Скалярное произведение может быть определено как проекция одного вектора на другой, умноженная на произведение другого вектора.
Изображение 2
Здесь a и b — два вектора, чтобы найти скалярное произведение между этими двумя векторами, мы сначала находим величину обоих векторов, а чтобы найти величину, мы используем теорему Пифагора или формулу расстояния.
После нахождения величины мы просто умножаем ее на угол косинуса между обоими векторами. Математически это можно записать как:
А . В = |А| cosθ * |B|
Где |А| cosθ — проекция A на B
И |Б| величина вектора B
Теперь в SVM нам нужна только проекция A, а не величина B, позже я объясню почему. Чтобы просто получить проекцию, мы можем просто взять единичный вектор B, потому что он будет в направлении B, но его величина будет равна 1. Следовательно, теперь уравнение принимает вид:
Чтобы просто получить проекцию, мы можем просто взять единичный вектор B, потому что он будет в направлении B, но его величина будет равна 1. Следовательно, теперь уравнение принимает вид:
А.В = |А| cosθ * единичный вектор B
Теперь давайте перейдем к следующей части и посмотрим, как мы будем использовать это в SVM.
Использование скалярного произведения в SVM:
Рассмотрим случайную точку X, и мы хотим знать, лежит ли она на правой стороне плоскости или на левой стороне плоскости (положительной или отрицательной).
Чтобы найти это, сначала предположим, что эта точка является вектором (X), а затем мы создадим вектор (w), перпендикулярный гиперплоскости. Предположим, что расстояние вектора w от начала координат до границы решения равно «c». Теперь возьмем проекцию вектора X на w.
Мы уже знаем, что проекция любого вектора или другого вектора называется скалярным произведением. Следовательно, мы берем скалярное произведение векторов x и w. Если скалярное произведение больше, чем «с», мы можем сказать, что точка лежит на правой стороне. Если скалярное произведение меньше «с», то точка находится слева, а если скалярное произведение равно «с», то точка лежит на границе решения.
Если скалярное произведение больше, чем «с», мы можем сказать, что точка лежит на правой стороне. Если скалярное произведение меньше «с», то точка находится слева, а если скалярное произведение равно «с», то точка лежит на границе решения.
Вы, должно быть, сомневаетесь, почему мы взяли этот перпендикулярный вектор w к гиперплоскости? Итак, нам нужно расстояние вектора X от границы решения, и на границе может быть бесконечное количество точек, от которых можно измерить расстояние. Вот почему мы приходим к стандарту, мы просто берем перпендикуляр и используем его в качестве эталона, а затем берем проекции всех других точек данных на этот перпендикулярный вектор, а затем сравниваем расстояние.
В SVM также есть понятие маржи. В следующем разделе мы увидим, как мы находим уравнение гиперплоскости и что именно нам нужно оптимизировать в SVM.
Поля в методе опорных векторов
Все мы знаем, что уравнение гиперплоскости имеет вид w. x+b=0, где w — вектор, нормальный к гиперплоскости, а b — смещение.
x+b=0, где w — вектор, нормальный к гиперплоскости, а b — смещение.
Чтобы классифицировать точку как отрицательную или положительную, нам нужно определить решающее правило. Мы можем определить правило принятия решения как:
Если значение w.x+b>0, то мы можем сказать, что это положительная точка, в противном случае это отрицательная точка. Теперь нам нужны (w,b) такие, чтобы поле имело максимальное расстояние. Допустим, это расстояние равно «d».
Для расчета d нам нужно уравнение L1 и L2. Для этого примем несколько предположений, что уравнение L1 равно w.x+b=1 , а уравнение L2 равно w.x+b=-1 . Теперь вопрос приходит
1. Почему величина равная, почему не взяли 1 и -2?
2. Почему мы взяли только 1 и -1, а не любое другое значение, например 24 и -100?
3. Почему мы взяли эту линию?
Попробуем ответить на эти вопросы:
1. Мы хотим, чтобы наша плоскость находилась на одинаковом расстоянии от обоих классов, что означает, что L должна проходить через центр L1 и L2, поэтому мы берем величину равной.
2. Допустим, уравнение нашей гиперплоскости 2x+y=2, мы видим, что даже если мы умножим все уравнение на какое-то другое число, линия не изменится (попробуйте построить на графике). Следовательно, для математического удобства мы принимаем его равным 1,9.0003
3. Теперь главный вопрос, а почему именно эту строку надо считать? Чтобы ответить на этот вопрос, я попытаюсь воспользоваться помощью графиков.
Предположим, что уравнение нашей гиперплоскости 2x+y=2:
Давайте создадим запас для этой гиперплоскости,
Если умножить эти уравнения на 10, мы увидим, что параллельная линия (красная и зеленая) приближается к нашей гиперплоскости. Для большей ясности посмотрите на этот график (https://www.desmos.com/calculator/dvjo3vacyp)
Мы также наблюдаем, что если мы разделим это уравнение на 10, то эти параллельные линии станут больше. Посмотрите на этот график (https://www.desmos.com/calculator/15dbwehq9).г).
Этим я хотел показать вам, что параллельные прямые зависят от (w,b) нашей гиперплоскости, если мы умножим уравнение гиперплоскости с коэффициентом больше 1, то параллельные прямые сожмутся, а если мы умножим с коэффициентом меньше чем 1, они расширяются.
Теперь мы можем сказать, что эти линии будут двигаться, когда мы изменяем (w,b), и вот как это оптимизируется. Но что такое функция оптимизации? Давайте посчитаем.
Мы знаем, что цель SVM состоит в том, чтобы максимизировать этот запас, который означает расстояние (d). Но ограничений на это расстояние (d) немного. Давайте посмотрим, что это за ограничения.
Функция оптимизации и ее ограничения
Чтобы получить нашу функцию оптимизации, нужно учесть несколько ограничений. Это ограничение заключается в том, что «Мы рассчитаем расстояние (d) таким образом, чтобы ни одна положительная или отрицательная точка не пересекала предельную линию». Запишем эти ограничения математически:
Вместо того, чтобы выдвигать вперед 2 ограничения, мы попробуем упростить эти два ограничения до 1. Мы предполагаем, что отрицательные классы имеют y=-1 и положительные классы имеют y=1 .
Можно сказать, что для правильной классификации каждой точки всегда должно выполняться это условие:
Предположим, что зеленая точка правильно классифицирована, что означает, что она будет следовать w. x+b>=1, , если мы умножим это на y=1 , мы получим то же самое уравнение, упомянутое выше. Точно так же, если мы сделаем это с красной точкой с y=-1 , мы снова получим это уравнение . Следовательно, мы можем сказать, что нам нужно максимизировать (d) так, чтобы это ограничение выполнялось.
x+b>=1, , если мы умножим это на y=1 , мы получим то же самое уравнение, упомянутое выше. Точно так же, если мы сделаем это с красной точкой с y=-1 , мы снова получим это уравнение . Следовательно, мы можем сказать, что нам нужно максимизировать (d) так, чтобы это ограничение выполнялось.
Возьмем 2 опорных вектора, 1 из отрицательного класса и 2 и из положительного класса. Расстояние между этими двумя векторами x1 и x2 будет равно (x2-x1) вектору . Что нам нужно, так это кратчайшее расстояние между этими двумя точками, которое можно найти с помощью трюка, который мы использовали в скалярном произведении. Мы берем вектор «w», перпендикулярный гиперплоскости, а затем находим проекцию вектора (x2-x1) на «w». Примечание: этот перпендикулярный вектор должен быть единичным вектором, тогда только он будет работать. Почему это должен быть единичный вектор? Это было объяснено в разделе точечного произведения. Чтобы сделать этот «w» единичным вектором, мы разделим его на норму «w».
Мы уже знаем, как найти проекцию вектора на другой вектор. Мы делаем это скалярным произведением обоих векторов. Итак, давайте посмотрим, как
Так как x2 и x1 являются опорными векторами и лежат на гиперплоскости, то они будут следовать y i * (2.x+b)=1 поэтому мы можем записать это как:
Подставляя уравнения (2) и (3) в уравнение (1) получаем:
Следовательно, уравнение, которое мы должны максимизировать:
Теперь мы нашли нашу функцию оптимизации, но здесь есть загвоздка в том, что мы не находим этот тип идеально линейно разделимых данных в отрасли, почти ни в одном случае мы не получаем этот тип данных и, следовательно, мы не можем использовать это условие мы доказали здесь. Тип задачи, которую мы только что изучили, называется Hard Margin SVM теперь мы будем изучать мягкую маржу, которая похожа на эту, но есть еще несколько интересных приемов, которые мы используем в Soft Margin SVM.
Мягкая маржа SVM
В реальных приложениях мы не находим ни одного набора данных, который был бы линейно разделим, мы найдем либо почти линейно разделимый набор данных, либо нелинейно разделимый набор данных. В этом сценарии мы не можем использовать трюк, который мы доказали выше, потому что он говорит, что он будет работать только тогда, когда набор данных полностью линейно разделим.
В этом сценарии мы не можем использовать трюк, который мы доказали выше, потому что он говорит, что он будет работать только тогда, когда набор данных полностью линейно разделим.
Чтобы решить эту проблему, мы модифицируем это уравнение таким образом, чтобы оно допускало мало ошибочных классификаций, что означает, что оно допускало неправильную классификацию нескольких точек.
Мы знаем, что max[f(x)] также можно записать как min[1/f(x)] , общепринятой практикой является минимизация функции стоимости для задач оптимизации; следовательно, мы можем инвертировать функцию.
Чтобы составить уравнение с мягкой границей, мы добавим к этому уравнению еще 2 члена: дзета и умножить на гиперпараметр «c»
для всех , правильно классифицированных баллов. мы видим неправильно классифицированные зеленые точки, значение дзета будет расстоянием этих точек от гиперплоскости L1 и для неправильно классифицированной красной точки дзета будет расстоянием этой точки от гиперплоскости L2.
Итак, теперь мы можем сказать, что это SVM Error = Margin Error + Classification Error. Чем выше маржа, тем меньше возможная маржинальная ошибка, и наоборот.
Допустим, вы берете высокое значение «c» = 1000, это будет означать, что вы не хотите сосредотачиваться на маржинальной ошибке и просто хотите получить модель, которая не неправильно классифицирует ни одну точку данных.
Посмотрите на рисунок ниже.
Если кто-то спросит вас, какая модель лучше, та, где маржа максимальна и есть 2 неправильно классифицированные точки, или та, где маржа очень меньше, и все точки классифицированы правильно?
Ну, на этот вопрос нет правильного ответа, но мы можем использовать SVM Error = Margin Error + Classification Error, чтобы оправдать это. Если вы не хотите, чтобы в модели была какая-либо неправильная классификация, вы можете выбрать рисунок 2 . Это означает, что мы увеличим «c», чтобы уменьшить ошибку классификации, но если вы хотите, чтобы ваша маржа была максимальной, значение «c» должно быть минимальным. Вот почему «c» — это гиперпараметр, и мы находим оптимальное значение «c», используя GridsearchCV и перекрестную проверку.
Вот почему «c» — это гиперпараметр, и мы находим оптимальное значение «c», используя GridsearchCV и перекрестную проверку.
Давайте двигаться дальше и теперь узнаем об очень хорошем трюке под названием «Трюк с ядром» .
Ядра в машине опорных векторов
Самая интересная особенность SVM заключается в том, что он может работать даже с нелинейным набором данных, и для этого мы используем «Kernel Trick», который упрощает классификацию точек. Предположим, у нас есть такой набор данных:
.Источник изображения: Автор
Здесь мы видим, что не можем провести ни одной линии или, скажем, гиперплоскости, которая могла бы правильно классифицировать точки. Итак, что мы делаем, так это пытаемся преобразовать это пространство более низкой размерности в пространство более высокой размерности, используя некоторые квадратичные функции, которые позволят нам найти границу решения, которая четко разделяет точки данных. Эти функции, которые помогают нам в этом, называются ядрами, и то, какое ядро использовать, определяется исключительно настройкой гиперпараметров.
Изображение 3
Ниже приведены некоторые функции ядра, которые вы можете использовать в SVM:
1. Полиномиальное ядро Ниже приведена формула ядра полинома:
Здесь d — степень многочлена, которую нам нужно указать вручную.
Предположим, у нас есть две функции X1 и X2 и выходная переменная Y, поэтому, используя полиномиальное ядро, мы можем записать ее как:
Итак, нам нужно найти X 1 2 , X 2 2 и X1.X2, и теперь мы видим, что 2 измерения были преобразованы в 5 измерений.
Изображение 4 2. Сигмовидное ядро Мы можем использовать его как прокси для нейронных сетей. Уравнение:
Он просто берет ваши входные данные, сопоставляя их со значениями 0 и 1, чтобы их можно было разделить простой прямой линией.
Источник изображения: https://dataaspirant.com/svm-kernels/#t-1608054630725
3.
 Ядро RBF
Ядро RBF На самом деле он создает нелинейные комбинации наших функций, чтобы поднять ваши выборки в многомерное пространство признаков, где мы можем использовать линейную границу решения для разделения ваших классов. Это наиболее часто используемое ядро в классификациях SVM, следующее формула объясняет это математически:
где,
1. «σ» — это дисперсия и наш гиперпараметр
2. || X₁ – X₂ || — Евклидово расстояние между двумя точками X₁ и X₂
Изображение 5
4. Ядро функции БесселяВ основном используется для устранения перекрестного члена в математических функциях. Ниже приведена формула ядра функции Бесселя:
5. Ядро AnovaОн хорошо работает с задачами многомерной регрессии. Формула для этой функции ядра:
Как правильно выбрать ядро?
Мне хорошо известно, что у вас должны быть сомнения относительно того, как решить, какая функция ядра будет эффективно работать с вашим набором данных. Необходимо выбрать хорошую функцию ядра, поскольку от этого зависит производительность модели.
Необходимо выбрать хорошую функцию ядра, поскольку от этого зависит производительность модели.
Выбор ядра полностью зависит от того, с каким набором данных вы работаете. Если это линейно разделимо, вы должны выбрать. для линейной функции ядра, так как она очень проста в использовании, а сложность намного ниже по сравнению с другими функциями ядра. Я бы рекомендовал вам начать с гипотезы о том, что ваши данные линейно разделимы, и выбрать линейную функцию ядра.
Затем вы можете перейти к более сложным функциям ядра. Обычно мы используем SVM с RBF и линейной функцией ядра, потому что другие ядра, такие как полиномиальное ядро, используются редко из-за низкой эффективности. Но что, если и линейный, и RBF дают примерно одинаковые результаты? Какое ядро теперь выбираем? Давайте разберемся с этим на примере, для простоты я возьму только 2 функции, которые означают только 2 измерения. На рисунке ниже я нанес границу решения линейного SVM для 2 функций набора данных радужной оболочки:
Изображение 6
Здесь мы видим, что линейное ядро отлично работает на этом наборе данных, а теперь посмотрим, как будет работать ядро RBF.
Мы видим, что оба ядра дают одинаковые результаты, оба хорошо работают с нашим набором данных, но какое из них выбрать? Линейный SVM — это параметрическая модель. Параметрическая модель — это концепция, используемая для описания модели, в которой все ее данные представлены в ее параметрах. Короче говоря, единственная информация, необходимая для прогнозирования будущего на основе текущего значения, — это параметры.
Сложность ядра RBF возрастает по мере увеличения размера обучающих данных. В дополнение к тому, что подготовка ядра RBF обходится дороже, мы также должны поддерживать матрицу ядра, а проекция в это «бесконечное» многомерное пространство, где данные становятся линейно разделимыми, также обходится дороже во время прогнозирования. Если набор данных нелинейный, то использование линейного ядра не имеет смысла, мы получим очень низкую точность, если сделаем это.
Изображение 8Таким образом, для такого набора данных мы можем использовать RBF даже не задумываясь, потому что он определяет границы решения следующим образом:
Изображение 9 Внедрение и настройка гиперпараметров машины опорных векторов в Python Для реализации набора данных мы будем использовать набор данных Income Evaluation, который содержит информацию о личной жизни человека и результат 50 000 или <= 50. Набор данных можно найти здесь (https://www.kaggle.com/lodetomasi1995/income-classification)
Набор данных можно найти здесь (https://www.kaggle.com/lodetomasi1995/income-classification)
Задача здесь состоит в том, чтобы классифицировать доход человека при наличии необходимых исходных данных о его личной жизни.
Сначала импортируем все необходимые библиотеки.
# Импортировать все соответствующие библиотеки
из sklearn.svm импортировать SVC
импортировать numpy как np
импортировать панд как pd
из sklearn.preprocessing импортировать StandardScaler
из sklearn.model_selection импорта train_test_split
импорт из sklearn.metrics: точность_оценки, путаница_матрица
предварительная обработка импорта из sklearn
предупреждения об импорте
предупреждения.filterwarnings("игнорировать")
Теперь давайте прочитаем набор данных и посмотрим на столбцы, чтобы лучше понять информацию.
df = pd.read_csv('income_evaluation.csv') df.head()
Я уже сделал часть предварительной обработки данных, и вы можете посмотреть весь код здесь. Здесь моя основная цель — рассказать вам, как реализовать SVM на python.
Здесь моя основная цель — рассказать вам, как реализовать SVM на python.
Теперь для обучения и тестирования нашей модели данные должны быть разделены на обучающие и тестовые данные.
Мы также масштабируем данные, чтобы они находились в диапазоне от 0 до 1.
# Разделить набор данных на тестовые и обучающие данные
X_train, X_test, y_train, y_test = train_test_split(df.drop('доход', ось=1),df['доход'], test_size=0,2) Теперь давайте продолжим определение классификатора опорных векторов вместе с его гиперпараметрами. Далее мы подгоним эту модель к обучающим данным.
# Определить классификатор опорных векторов с гиперпараметрами
svc = SVC (случайное_состояние = 101)
точность = cross_val_score(svc,X_train,y_train,cv=5)
svc.fit(X_train,y_train)
print("Оценка поезда:"np.mean(accuracies)) printf("Оценка теста:"svc.score(X_test,y_test)) Модель обучена, и теперь мы также можем наблюдать за выходными данными.
Ниже вы можете увидеть точность набора данных теста и обучения
Вы даже можете гипертюнинговать свою модель по следующему коду:
сетка = {'С':[0.01,0.1,1,10],
'ядро': ["линейный","поли","rbf","сигмоид"],
'степень' : [1,3,5,7],
«гамма»: [0,01,1]
}
свм = СВК ()
svm_cv = GridSearchCV (svm, сетка, cv = 5)
svm_cv.fit(X_train,y_train)
print("Лучшие параметры:", svm_cv.best_params_) print("Оценка поезда:", svm_cv.best_score_) print("Оценка теста:", svm_cv.score(X_test,y_test))
Набор данных довольно большой, и, следовательно, потребуется время для обучения, по этой причине я не могу вставить результат приведенного выше кода здесь, потому что SVM плохо работает с большими наборами данных, требуется много времени, чтобы получить обученный.
Преимущества SVM 1. SVM работает лучше, когда данные являются линейными
SVM работает лучше, когда данные являются линейными
2. Более эффективен в больших размерах
3. С помощью трюка с ядром мы можем решить любую сложную проблему
4. SVM не чувствителен к выбросам
5. Может помочь нам с классификацией изображений
Недостатки SVM1. Выбрать хорошее ядро непросто
2. Не показывает хороших результатов на большом наборе данных
3. Гиперпараметрами SVM являются Cost-C и gamma. Не так-то просто точно настроить эти гиперпараметры. Трудно представить себе их влияние
Конец ПримечанияВ этой статье мы подробно рассмотрели очень мощный алгоритм машинного обучения, метод опорных векторов. Я обсудил его концепцию работы, математическую интуицию за SVM, реализацию на питоне, приемы классификации нелинейных наборов данных, плюсы и минусы, и, наконец, мы решили проблему с помощью SVM.
Об авторе В настоящее время я учусь на последнем курсе по статистике (бакалавр статистики) и очень интересуюсь наукой о данных, машинным обучением и искусственным интеллектом. Мне нравится погружаться в данные, чтобы обнаруживать тенденции и другие ценные сведения о данных. Я постоянно учусь и мотивирован пробовать что-то новое.
Мне нравится погружаться в данные, чтобы обнаруживать тенденции и другие ценные сведения о данных. Я постоянно учусь и мотивирован пробовать что-то новое.
Открыт к сотрудничеству и работе.
При возникновении любых сомнений и вопросов, не стесняйтесь обращаться ко мне по электронной почте
Свяжитесь со мной в LinkedIn и Twitter
Источник изображения:
- Изображение 1: https://www.javatpoint.com/machine-learning-support-vector-machine-algorithm
- Изображение 2: https://byjus.com/maths/dot-product-of-two-vectors/
- Изображение 3: https://medium.com/@zxr.nju/what-is-the-kernel-trick-why-is-it-important-98a98db0961d
- Изображение 4: https://www.oreilly.com/library/view/machine-learning-quick/9781788830577/fc007e8f-36a8-4d27-8e22-5d4d82270cdf.xhtml
- Изображение 5: https://dataaspirant.com/svm-kernels/#t-1608054630725
- Изображение 6: https://www.kdnuggets.com/2016/06/select-support-vector-machine-kernels.


 Подраздел 1.2 «Сведения о страховом стаже» раздела 1
Подраздел 1.2 «Сведения о страховом стаже» раздела 1
 № ЕД-7-11/881@
№ ЕД-7-11/881@ Подраздел 3 «Сведения о застрахованных лицах, за которых перечислены дополнительные страховые взносы на накопительную пенсию и уплачены взносы работодателя»
Подраздел 3 «Сведения о застрахованных лицах, за которых перечислены дополнительные страховые взносы на накопительную пенсию и уплачены взносы работодателя»
Об авторе