Среднесписочная численность это: Среднесписочная численность работников, как рассчитать ССЧ за год в 2021

Содержание

В чем разница и отличия средней численности работников от среднесписочной

Существует множество видов численности сотрудников на предприятии важных для бухгалтерских расчетов. В этой статье речь пойдёт о средней и среднесписочной численности.

Содержание статьи

Что такое средняя и среднесписочная численность

Средняя численность — это составной показатель, она включает:

среднесписочную численность сотрудников;
количество лиц, занятых на данном предприятии в качестве внешних совместителей, иначе говоря, имеющих основное место работы в другой организации;
число сотрудников, которые работают на данном предприятии на основании гражданско-правового договора.

Данное понятие определяется как среднее списочное количество персонала, которое определяется для заданного промежутка времени. Чаще всего этот параметр рассчитывается для месяца, квартала и, наконец, года, однако допускается и его вычисление для полугодия, а также любого иного количества месяцев.

При этом помесячные данные служат основой для калькуляций среднесписочной численности для более длительных периодов.

Вычислять эту величну может потребоваться для следующих целей:

для предоставления сведений о среднесписочной численности сотрудников в данной организации за истёкший год. Такую информацию требуется предоставить в локальный орган налоговой службы не позднее 20 января года, следующего за истёкшим;
предприятия, которые только что образовались либо пережили реорганизацию, обязаны предоставить такой показатель в месяц, следующий за тем, когда компания была создана или сменила форму также не позднее 20 числа;
для определения, требуется ли предприятию предоставлять в налоговую службу в электронном виде налоговую декларацию, её требуется отправить всем организациям, у которых данный показатель превышает 100 человек;
если в компании трудится меньшее количество народа, то она обязана известить налоговую инспекцию о среднесписочной численности персонала, но обязанность подавать её именно в электронном виде для неё отсутствует;

в свою очередь индивидуальные предприниматели должны предоставлять эту информацию, только если они нанимали сотрудников в течение предыдущего года;
для внесения соответствующей информации в форме РСВ-1 Пенсионного фонда, которая содержит поле «Среднесписочная численность»;
для внесения информации в поле «Численность работников» в форме 4-ФСС;
для вычисления значения авансового платежа по налогу с прибыли, взимаемого с обособленного подразделения организации

В чём отличия понятий

Отличие средней от среднесписочной численности состоит в том, что среднесписочная численность представляет собой более узкое понятие, она входит в среднюю.

При этом числовые значения двух этих категорий могут быть сходны, поскольку наряду со среднесписочной в среднюю численность включают усреднённый показатель численности для внешних совместителей, а также сотрудников, которые трудятся в компании по гражданско-правовым договорам. Поэтому если на предпритии нет таких сотрудников, то числовые значения могут совпадать.

Как производятся расчёты

Так как среднесписочная численность входит в качестве составной части в среднюю численность, в первую очередь требуется вычислить именно среднесписочную. Среднесписочная численность определяется на основе средней численности для определённого месяца, которую делят на число дней в месяце.

При этом стоит иметь в виду, что некоторые категории сотрудников, входящие в списочную численность, исключаются из неё при вычислении среднесписочной. Есть и категории, которые, напротив, включаются в среднесписочную численность, хотя в списочной их не учитывают.

Далее средняя численность определяется прибавлением к среднесписочной двух других компонентов.

Среднесписочная

Определение среднесписочной численности выполняется для промежутков от месяца (минимальный) до года (максимальный).

Прежде всего, устанавливают списочную численность для сотрудников организации.

В рабочие дни в такую численность включают всех сотрудников, которые работают в организации на основании трудового договора, прибавляя к ним и персонал, который отсутствует на рабочем месте вследствие нетрудоспособности временного характера при условии оформления ими больничных листов. Также учитывают лиц, отправленные в различные отпуска и служебные поездки.

Кроме того, в расчёт принимают:

лиц, работающих на дому в соответствии с трудовым договором;
работников, получивших выходной на основании работы в выходные или праздничные дни;
сотрудников, отправленных в учебные отпуск, при условии начисления им за этот период заработной платы либо в полном, либо в частичном объёме.

При этом сотрудники, которые работают в организации неполное время, учитываются в соответствующий день в пропорции к отработанным часам.

При этом существует ряд категорий, относящихся к списочной численности, которые при этом не включаются в расчёт среднесписочной:

внешние совместители, имеющие основное место работы в иной организации;
сотрудницы, которые ушли в отпуск либо период беременности и родов либо на время ухода за ребёнком;
лица, которым предоставлен учёбный отпуск без оплаты;
сотрудники, для которых установлена неполная занятость, включая как неполный рабочий день, так и неполную неделю;
сотрудники, которые работают в организации на основании гражданско-правового договора.

С другой стороны существует и категория, которая не включается в списочную численность, однако при расчёте среднесписочной их, напротив, надо учитывать. Это работники, которые трудятся в организации на основании договоров специального характера, заключённых с государственными учреждениями. К ним относятся лица, находящиеся в местах лишения свободы или служащие в вооружённых силах. Работники, относящиеся к такому контингенту, во все дни, когда они были на рабочем месте, учитываются, как единица и прибавляются к списочной численности.

В выходные дни, равно как и в праздники, в качестве списочной численности рассматривают показатель, установленный для предыдущего рабочего дня перед этим нерабочим.

В частности, если сотрудник был уволен в пятницу, то для следующих за ней субботы и воскресенье он ещё учитывается в списочной численности.

Вышеописанным образом определяется списочная численность для всех дней по отдельности.

Далее требуется для каждого отдельного календарного месяца сложить показатели списочной численности, определённые для всех его дней, включая выходные и праздники. Вслед за этим требуется эти величины разделить на число дней в месяце, то есть либо на 30 или на 31, исключая февраль, где делителем станет число 28 или 29.

Частное и будет среднесписочной численностью для месяца.

Вычисление среднесписочной численности за год либо квартал или полугодие, либо за иное число месяцев осуществляется путём сложения величин среднесписочной численности для соответствующих календарных месяцев и последующего деления на их число. Полученный итог необходимо округлить до целого числа, отбросив дробь, если она менее 0,5 и прибавив единицу, если она превосходит 0,5.

Средняя

Уже после того, как определена списочная численность, а далее на её основе — среднесписочная, на основании этой последней в свою очередь рассчитывается и средняя.

Выше уже упоминалось, что, наряду со среднесписочной численности работников для её определения также требуется учитывать среднюю численности сотрудников со статусом внешних совместителей, а также среднюю численность лиц на гражданско-правовом договоре.

Внешние совместители принимаются в расчёт пропорционально времени, которое они протрудились на предприятии.

Сотрудники, заключившие гражданско-правовой договор, учитываются как единицы за все дни, в продолжение которых этот договор был в силе, далее сумму этих единиц делят на общее число дней в месяце.

Списочная численность представляет собой сумму этих трёх показателей. На практике, разумеется, основной вклад в списочную численность обычно вносит именно среднесписочная, поэтому разница между ними в большинстве случаев не слишком существенна.

Данное видео наглядно демонстрирует, как рассчитать численность.

Среднесписочная численность работников — формула расчета и понятие

ССЧ персонала – расчетная величина за указанный период, необходима учета в налоговой и прочих надзорных органах. Законы РФ предписывают индивидуальным предпринимателям и директорам каждый год сообщать эти сведения в органы учета.

Данные о ССЧ персонала

Данные ССЧ нужны для оформления различных документов, к примеру:

подтверждение льгот при налоговой проверке;
показывает ключевые коэффициенты работы компании;
сведения о персонале;
отслеживание обязательных сборов в фонды.

Все сведения направляются в налоговую службу, и прочие надзорные органы.

Формула для расчета ССЧ

Каждый год показатели ССЧ компании нужно передавать в органы надзора до 20 января. Проще говоря, в органы надзора нужно направить бумаги о персонале до 20 января. Конечно, существуют и послабления со сроками, к примеру, если компании была зарегистрирована за несколько недель до этого числа.

Высчитать ССЧ очень просто, ведь существует специальная формула. Нужно лишь посчитать годовую численность штата и поделить его на 12. Ежемесячный расчет производится по следующий формуле:

ССЧ (месяц) = Σ ССЧ (день)/ К (день)

где:

Σ ССЧ (день) – усредненная сумма количества людей за рабочие дни месяца;

К (день) – число рабочих дней в месяце;

Из этой формулы легко вывести формулу для годового расчета:

ССЧ (год) = Σ ССЧ (месяц)/12

где:

Σ ССЧ (месяц) – сумма ежемесячного объема прошлогодних показателей ССЧ.

Для квартальных расчетов используется следующая формула:

ССЧ (кварт.) = Σ ССЧ (месс. кварт.)/3,

где:

Σ ССЧ (месс. кварт.) – сумма работников за учетный квартал.

Во время расчетов, не забывайте, что количество работающих людей в праздники или выходные равны показателям рабочего дня. Рассчитывая ежемесячный ССЧ не забывайте про нижеуказанные факторы:

наличие людей на рабочих местах, и учет людей, не выходящих на работу из-за простоя компании;
рабочие, не находящиеся на работе, по причине поездки по делам фирмы или повышения квалификации;

персонал на больничном;
прогульщики;
специалисты, работающие на неполную ставку или смену;
участники забастовок;
работники, которые работают и учатся заочно;
люди на плановом отпуске;
сотрудники компании в отгулах;
сотрудники, работающие по фактам.

Также в ССЧ не учитывается следующий персонал:

люди, работающие по гражданско-правовому соглашению;
область юридической защиты;
сотрудники, проходящие срочную службу в армии;
управляющие компанией, которым не перечисляется заработная плата;
участники кооператива, отказавшиеся подписывать трудовое соглашение;
работники, переведенные в другую компанию без сохранения текущей зарплаты;
работники, которых нанимают по договору с государственными службами;
работники, отправленные компанией на переквалификацию, или повышение квалификации с выплатой стипендии;
люди, которые работают и представляют интересы сразу нескольких компаний.

Среднесписочная численность и фактическая отличается

Планируя свой бизнес, предприниматель рассчитывает количество людей, нужных для выполнения рабочих задач. Штат может насчитывать несколько десятков человек или, напротив, сотни и даже тысячи сотрудников. Всё зависит от возможностей руководства, направления работы и уровня компании. В этой статье основное внимание будет уделено понятию фактической численности работников , методике подсчёта, а также документальному сопровождению.

ВИДЕО ПО ТЕМЕ: Cведения о среднесписочной численности

Дорогие читатели! Наши статьи рассказывают о типовых способах решения юридических вопросов, но каждый случай носит уникальный характер.

Если вы хотите узнать, как решить именно Вашу проблему — обращайтесь в форму онлайн-консультанта справа или звоните по телефонам, представленным на сайте. Это быстро и бесплатно!

Фактическая численность работников

Поэтому знать разницу и отличия списочной и среднесписочной численности нужно обязательно. Оглавление: 1. Списочная и среднесписочная численность — что это такое 2. Чем отличается списочная численность от среднесписочной численности — разница. Списочная и среднесписочная численность — что это такое Численность сотрудников предприятия является одним из важнейших кадровых показателей.

Это связано с тем, что действующее законодательство считает численность работников одним из основных критериев определения размеров предприятия. И, как следствие — возможности применения им особых режимов налогообложения и подачи отчетности. Поэтому работодателю важно всегда понимать, какой является численность сотрудников на предприятии.

При этом тяжело найти компанию, в которой численность работников всегда была бы постоянной величиной. Работники могут увольняться, штатное расписание может изменяться. Поэтому для того, чтобы скомпенсировать такие возможные флуктуации численности сотрудников предприятия и было использовано понятие среднесписочной численности.

Среднесписочная численность — это усредненное количество работников предприятия в течение определенного периода. Использование этого показателя позволяет получить информацию о количестве работников в среднем в компании в течение определенного учетного промежутка времени. Более подробно о том, что такое среднесписочная численность сотрудников можно прочитать в отдельной статье.

Простая же списочная численность — это непосредственное количество работников, которые находятся на предприятии по состоянию на какую-либо конкретную дату. В расчетах списочной численности сотрудников участвуют только лица, которые находятся в штате предприятия в конкретный день. Как можно понять из толкования самих понятий списочной и среднесписочной численности, главное отличие этих показателей — это порядок их расчета.

Для определения списочной численности необходимо посчитать количество штатных единиц, исключая из списка фактических работников внешних совместителей, лиц, работающих по гражданско-правовым договорам, а также лиц, не явившихся на работу при отсутствии уважительной причины, когда ими уже было написано заявление на увольнение. Декретницы и люди, находящиеся на больничном, относятся к списочному составу.

Почти все эти же лица за редкими исключениями в такой же мере учитываются в среднесписочной численности трудящихся. Однако, необходимо учитывать все конкретные дни периода, за который рассматривается среднесписочная численность. Таким образом, одно из основных отличий рассматриваемых понятий — это то, что для определения среднесписочной численности необходимо знание списочной.

При этом также есть разница и в сложности проведения расчетов. Списочную численность определить достаточно легко, в то время как среднесписочная потребует проведения определенных вычислений. Также, списочная численность сотрудников предполагает использование исключительно целых показателей количества работников. В то же время усредненные показатели могут быть дробными, так как количество работников может меняться в зависимости от рассматриваемых периодов.

С этим читают С этим читают Несписочный состав работников — что это такое, чем отличается от штата Срок сдачи отчета о среднесписочной численности в году Фактическая численность работников Штатная численность Автор: Архипова Ольга Сергеевна 18 голос. Да, добавьте меня в свой список рассылки.

Еще одно важное отличие списочной численности от среднесписочной — это категории лиц, не включаемых в число сотрудников. Так, не входят в среднесписочную, но входят в списочную численность лица, направленные на обучение, сотрудники, командированные за границу , а также работники в декретных отпусках по беременности и родам, усыновлению или же уходу за ребенком.

С этим читают С этим читают. Несписочный состав работников — что это такое, чем отличается от штата. Срок сдачи отчета о среднесписочной численности в году. Фактическая численность работников.

Штатная численность. Автор: Архипова Ольга Сергеевна. Обсуждение 0 показать еще. Поделитесь своим мнением Нажмите, чтобы отменить ответ.

Фактическая численность и среднесписочная численность

Предельная и фактическая численность работников — это важные показатели, характеризующие необходимое количество персонала для достижения главной цели финансово-хозяйственной деятельности предприятия — получения прибыли. При этом предельная подразумевает под собой максимальное количество сотрудников, необходимых для выполнения работы, а фактическая отражает реальное положение дел. Списочная и фактическая численность работников — это разновидности, главное отличие которых в том, что первая иллюстрирует общее количество сотрудников на предприятии с учетом находящихся в отпусках, декретах, больничных и т. Факторы, влияющие на потребность организации в персонале, можно разделить на 2 большие группы: внутренние и внешние.

Также Вы можете бесплатно проконсультироваться у юристов онлайн прямо на сайте. В прерывных производствах КСП определяется как отношение табельного номинального фонда времени к плановому эффективному , а в непрерывных — как отношение календарного фонда времени к плановому эффективному.

Для составления отчетности в налоговые органы, подтверждения фискальных льгот и определения размера отдельных бюджетных обязательств фирмам и предпринимателям приходится определять показатели, связанные с количеством наемных специалистов. Разница средней численности и среднесписочной численности до сих остается непонятной для многих руководителей и сотрудников бухгалтерии. Рассмотрим, в чем отличие между понятиями и для каких целей они применяются в реальной экономической жизни. Действующее законодательство выделяет категории специалистов, которых не нужно включать в расчет вне зависимости от того, какой показатель определяется: средняя СЧ или среднесписочная численность ССЧ.

Списочная и среднесписочная численность работников

Каждый специалист по кадровому делу, руководитель или бухгалтер должен знать, чем отличается списочная численность от среднесписочной численности сотрудников предприятия. Эти понятия хоть и являются схожими, однако неправильное их использование может привести к серьезным неблагоприятным последствиям для компании. Поэтому знать разницу и отличия списочной и среднесписочной численности нужно обязательно. Оглавление: 1. Списочная и среднесписочная численность — что это такое 2. Чем отличается списочная численность от среднесписочной численности — разница. Списочная и среднесписочная численность — что это такое Численность сотрудников предприятия является одним из важнейших кадровых показателей. Это связано с тем, что действующее законодательство считает численность работников одним из основных критериев определения размеров предприятия. И, как следствие — возможности применения им особых режимов налогообложения и подачи отчетности. Поэтому работодателю важно всегда понимать, какой является численность сотрудников на предприятии.

Чем отличается списочная численность от фактической

Рано или поздно предприниматель нанимает в компанию сотрудников. По мере роста бизнеса увеличивается и штатная численность организации. Чем больше персонала, тем сложнее становится определение того, какая же у вас фактическая численность работников. Нужно разобраться, для чего нужен этот показатель и как его рассчитать за 1 отчетный период.

Списочная и среднесписочная численность работников Численность работников списочного состава — количественный показатель списочного состава, приводящийся на заданную дату, а также в среднем за отчетный период которым может быть месяц, квартал, год с его начала. Именно усредненный показатель чаще всего необходим для статистических и налоговых целей, а также для определения средней заработной платы, эффективности труда, коэффициентов оборота и других показателей.

Во избежание путаницы разберемся в соотношении этих двух понятий. Это важный показатель, отражающий сегмент деятельности организации и показывающий количество трудящихся в ней лиц на определенную дату или период. Именно усредненный показатель чаще всего необходим для статистических и налоговых целей, а также для определения средней заработной платы, эффективности труда, коэффициентов оборота и других показателей. При этом каждый работник учитывается в ней только однажды и как одна единица; включаются туда как фактически работающие лица, так и отсутствующие на работе.

Чем отличается списочная численность от среднесписочной

ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Как рассчитать среднесписочную численность работников? Часть 2. Работники с неполной занятостью

Фактическая численность работников это

Списочная и фактическая численность работников — это разновидности, главное отличие которых в том, что первая иллюстрирует.

Как расчитать среднесписочную численность работников при неполном рабочем дне

Ежегодно, не позднее 20 января, ООО и индивидуальные предприниматели должны сдавать сведения о среднесписочной численности работников за предыдущий год. Причем, ИП сдают этот отчёт только при наличии работающих в штате, а юридические лица — независимо от наличия персонала. Бланк отчётности КНД простой, содержит всего один значимый показатель, но расчёт среднесписочной численности работников надо делать с учетом требований Росстата, а это не всегда просто. Что такое среднесписочная численность работников и как её рассчитать? Прежде чем разобраться, что такое среднесписочная численность работников СЧР , надо понять, кто включается в списочную. Согласно Указаниям Росстата приказ от

ВИДЕО ПО ТЕМЕ: Расчет среднесписочной численности работников: формула, примеры

Среднесписочная численность в ФСС-4: расчет

Для расчета средней списочной численности за какой-либо другой период, необходимо сложить данный показатель за каждый месяц, который участвует в расчете, и разделить получившуюся сумму на количество месяцев за период. Допустим, что средняя списочная численность за февраль составила ,52 человека; за март — ,64 человека; за апрель — ,92 человека. В январе такой показатель был — ,74 человека. Оцените качество статьи.

При этом за дни болезни, отпуска, неявок в число отработанных человеко-часов условно включаются часы по предыдущему рабочему дню. Поясним на примере для обычной часовой 5-дневной рабочей недели.

Они учитываются за каждый отработанный день как 0,5 человека 4,0 : 8 часов ; — три сотрудника отработали по 3 часа в день 5, 7 и 22 рабочих дня соответственно. Бланк образец При расчёте следует помнить о том, что численность работников за выходной или праздничный день буден равна рабочему дню перед ним.

Учитываются за каждый календарный день. Таким образом, расчет среднесписочной численности сотрудников сводится к следующим действиям:. Ежегодно, не позднее 20 января, ООО и индивидуальные предприниматели должны сдавать сведения о среднесписочной численности работников за предыдущий год. Причем, ИП сдают этот отчёт только при наличии работающих в штате, а юридические лица — независимо от наличия персонала. Кроме того, не позже 20 числа месяца, следующего за тем, когда организация была создана, должны быть сданы.

Что такое среднесписочная численность работников и как её рассчитать? Прежде чем разобраться, что такое среднесписочная численность работников СЧР , надо понять, кто включается в списочную. Согласно Указаниям Росстата , в списочную численность включают принятых по , в том числе учредителей компании, если они получают зарплату.

Длительность трудового договора не имеет значения, учитываются даже те, кто проработал только один день. На предприятии работают по трудовому договору и по штатному расписанию 9 человек — все на 0,5 ставки. Для этого численность сотрудников с неполной занятостью определяйте пропорционально отработанному ими времени.

Из данной статьи вы узнаете, как правильно сотрудников, работающих неполный день, учитывать при расчете — как целые единицы или пропорционально отработанному времени. Работники, которые трудятся неполный рабочий день, при определении среднесписочной численности учитываются пропорционально отработанному времени.

Это следует из пункта Срочная новость для всех предпринимателей:. Подробности читайте в журнале Однако это правило не распространяется на работников:. Ответ на вопрос: В соответствии со ст. По его заявлению во время нахождения в отпуске по уходу за ребенком работник может трудиться на условиях неполного рабочего времени с сохранением права на получение пособия по государственному социальному страхованию.

Порядок расчета среднесписочной численности работников определен Указаниями по заполнению форм федерального статистического наблюдения N П Но прежде обращаем ваше внимание на важный момент.

В среднесписочную численность включают не всех работников из списочного состава п. Списочный состав — 2 человека, которые по собственной инициативе трудятся неполное рабочее время. Формула расчета списочной численности Списочная численность сотрудников определяется за каждый календарный день месяца. Причем если выходные или праздничные дни составляют несколько дней, то списочная численность работников за каждый этот день будет одинаковой и равной численности списочного состава за рабочий день, предшествующий выходным или праздникам.

Такое условие содержится в п. Пример 1. Установленный график работы — часовая пятидневная рабочая неделя. Списочная численность на 30 ноября — 25 человек. С 3 по 16 декабря включительно работник Иванов ушел в очередной ежегодный оплачиваемый отпуск.

Для замещения этой должности с 10 декабря на основании срочного трудового договора был принят работник Сидоров. Расчет среднесписочной численности работников Среднюю списочную численность за год определяют суммированием данного показателя за все месяцы года отчетного и делением получившейся суммы на Другие сотрудники, занятые в компании неполный рабочий день или неполную неделю на основании трудового договора или штатного расписания, рассчитываются, исходя из пропорционально отработанного времени.

Расчет среднесписочной численности таких работников производится за месяц в следующем порядке. Существует еще один способ расчета, более простой. Числа месяца Списочная численность работников Работники, исключаемые из списочной численности Работники, попавшие в среднесписочную численность 1 1 2 1 3 1 4 1 5 1 6 2 7 2 8 2 9 2 10 2 11 2 12 2 13 2 14 2 15 2 16 2 17 3 18 3 19 3 20 3 21 3 22 3 23 3 24 3 25 3 26 3 27 3 28 3 29 3 30 3 Итого: Общее количество работников списочного состава за весь календарный месяц, которые попадают в среднесписочную численность, составляет , число дней в месяце — В данном случае численность сотрудников за сентябрь составила человека : Пример расчета при неполной рабочей неделе На предприятии 5 сотрудников в сентябре г.

Средняя численность Для расчета этого показателя нам осталось определить среднюю численность внешних совместителей и лиц, выполняющих работу по договорам гражданско-правового характера. Алгоритм расчета средней численности внешних совместителей такой же, как и при расчете среднесписочной численности работников, трудящихся неполное рабочее время. Также в среднюю численность работающих по гражданско-правовым договорам не включаются индивидуальные предприниматели.

Таким документом необходимо руководствоваться при расчёте среднесписочной численности работников. Указания следует применять при заполнении форм и , предназначенной для Пенсионного фонда. Средняя численность персонала — показатель, от которого будет зависеть право учреждения на получение льгот, таких как, например: возможность применения упрощенной системы налогообложения, возможность сдачи упрощенной статистической отчетности, льгот по уплате НДС и др.

В среднюю численность включают:. Для подсчета средней списочной численности, сначала следует определить списочную численность работников за каждый день календарный отчетного периода. Ответив на поставленные вопросы, бухгалтер безошибочно осуществит подсчет показателя, и вовремя предоставит отчетность в контролирующие органы.

Среднесписочная численность работников ССЧ — отчет, сдаваемый в инспекцию федеральной налоговой службы до 20 января следующего за отчетным года. Отправка происходит ежегодно. Для расчета налогов и статистики используется среднестатистическая численность работников, сокращенно — ССЧ. Для расчета ССЧ сотрудников за месяц сложите их ежедневное списочное количество и разделите полученное значение на количество календарных дней в конкретном месяце.

При этом не забывайте, что в выходные и праздники ССЧ приравняется к численности сотрудников в предыдущий рабочий день. Также Вы можете бесплатно проконсультироваться у юристов онлайн прямо на сайте. Достаточно часто происходит ситуация, при которой в результате подсчетов получается не целое число, а дробное.

Как быть в этом случае? Нужно округлить. Именно бухгалтерам нужно внимательно ознакомиться с нашей статьей, чтобы верно произвести расчет и сдать налоговый отчет. Так что вы не сможете избежать необходимости рассчитывать среднесписочную численность, поэтому лучше это сделать сразу, чем ждать начисления штрафных санкций.

Продолжительность рабочего дня Количество рабочих часов в неделе При пятидневке, ч При шестидневке, ч 40 8 6,67 36 7,2 6 24 4,8 4 Действие 2. При упрощенном методе расчета средней численности не полностью занятых работников неполное рабочее время за день делится на продолжительность рабочего дня. Вначале рассчитывают среднесписочную численность за каждый месяц периода.

Затем суммируют все полученные среднесписочные и делят на количество месяцев в периоде. Как правильно рассчитать данный показатель для отчета. Пример вычисления. Когда необходимо знать эти сведения. Эта численность учитывается при определении среднесписочной численности работников.

Лица, работавшие неполное рабочее время по инициативе работодателя учитываются в среднесписочной численности работников как целые единицы. При этом нужно учитывать и данные следующих документов: приказов о приеме на работу, о нахождении в отпуске, о переводе на другую работу, о расторжении договора с сотрудником.

Некоторые сведения находятся в личной карте работника, расчетно-платежной ведомости или в других рабочих документах. Полученное округлим в большую сторону. В нерабочие дни численность берется как за предшествующий рабочий день. Сумма В данном примере сумма численности работников списочного состава за все дни месяца, подлежащих включению в среднесписочную численность, составляет , календарное число дней в месяце — 31, среднесписочная численность работников за месяц в этом случае составила человек : Численность показывается в целых единицах.

Среднесписочную численность работников за год рассчитывайте в соответствии с пунктами 78—83 новых Указаний, утвержденных приказом Росстата от Чтобы посчитать среднесписочную численность работников за месяц с несколькими рабочими днями, надо применить другой алгоритм. Например, ООО зарегистрировано 10 марта года, на работу по трудовому договору были приняты 25 человек, до конца марта списочный состав не менялся.

Если у Вас уже есть организация, и Вы думаете над тем, как облегчить и автоматизировать бухгалтерский учет и отчетность, то на помощь приходят следующие онлайн-сервисы, которые полностью заменят бухгалтера на Вашем предприятии и сэкономят много денег и времени. Для определения общей численности нужно сложить среднюю численность полностью занятых и частично занятых работников.

Итоговое значение округляется согласно математическим правилам — больше 0,5 вверх, а меньше — отбрасывается.

Для расчета среднесписочной численности работников за период с начала года по отчетный месяц включительно суммируется среднесписочная численность работников за все месяцы, истекшие за период с начала года по отчетный месяц включительно. Затем полученная сумма делится на число месяцев в этом периоде. В списочную численность до 14 января изначально должны быть включены 45 человек за исключением внешнего совместителя, не включаемого в данную численность; внутреннего совместителя, учитываемого по основной должности и должности, замещенной на условиях неполного рабочего времени, по которой подсчет должен производиться отдельно.

Если сотрудник работает в организации внешним совместителем, то в списочной численности он не учитывается. Другие более редкие исключения из подсчета списочной численности перечислены в п. Обратите внимание, что численность работников списочного состава за каждый день должна соответствовать данным табеля учета рабочего времени работников. Например, при расчете среднесписочной численности работников за год суммируют среднесписочную численность работников за все месяцы отчетного года.

Сумму делят на Если в штате предприятия состоят работники, которые трудятся неполный рабочий день, в списочной численности они числятся как целые единицы за каждый календарный день, включая нерабочие дни недели. Понятие С целью характеристики трудового потенциала организации используется система показателей.

Списочная численность — это количество работающих лиц на определенную дату с учетом движения персонала, то есть принятых и выбывших. Она включает всех сотрудников предприятия, в том числе тех, кто принят на работу. Прежде всего не учитываются при расчете показателя работники, не включаемые в списочную численность.

Как рассчитать среднесписочную численность работников за год?

Вход Регистрация. Что нового?

Среднесписочная численность — это показатель численности работников предприятия в среднем за определенный период времени. Очень часто понятие среднесписочная численность путают со средней численностью. Для того, чтобы разграничить эти показатели, нужно точно знать, где применяется каждый из этих показателей. Организации и индивидуальные предприниматели должны ежегодно подавать в налоговую инспекцию сведения о среднесписочной численности сотрудников за предыдущий год. Исключением являются предприниматели, которые в прошлом году не привлекали наемных сотрудников — им подавать не нужно.

Среднесписочная численность работников при неполном рабочем дне

Средняя численность шире среднесписочной. Бывают ситуации посложнее. Чтобы всё правильно посчитать, используйте пошаговую инструкцию. Введите свой e-mail, если хотите получить ответ. Войти в систему Возможности Цены Регистрация бизнеса. Справочная Блог. Все статьи по теме. Ольга Аввакумова. Попробовать Эльбу 30 дней бесплатно. Поделиться статьёй.

Образец расчета среднесписочной численности работников

Календарь бухгалтера Проверка контрагента Трудовой кодекс Налоговый кодекс. Образец расчета среднесписочной численности работников. Расчет среднесписочной численности работников за год — это отчет, который до 21 января года все организации и индивидуальные предприниматели, имеющие наемных работников, обязаны направить в территориальные органы ФНС России. Такие данные необходимы налоговикам для определения категории налогоплательщика и исчисления некоторых видов налогов.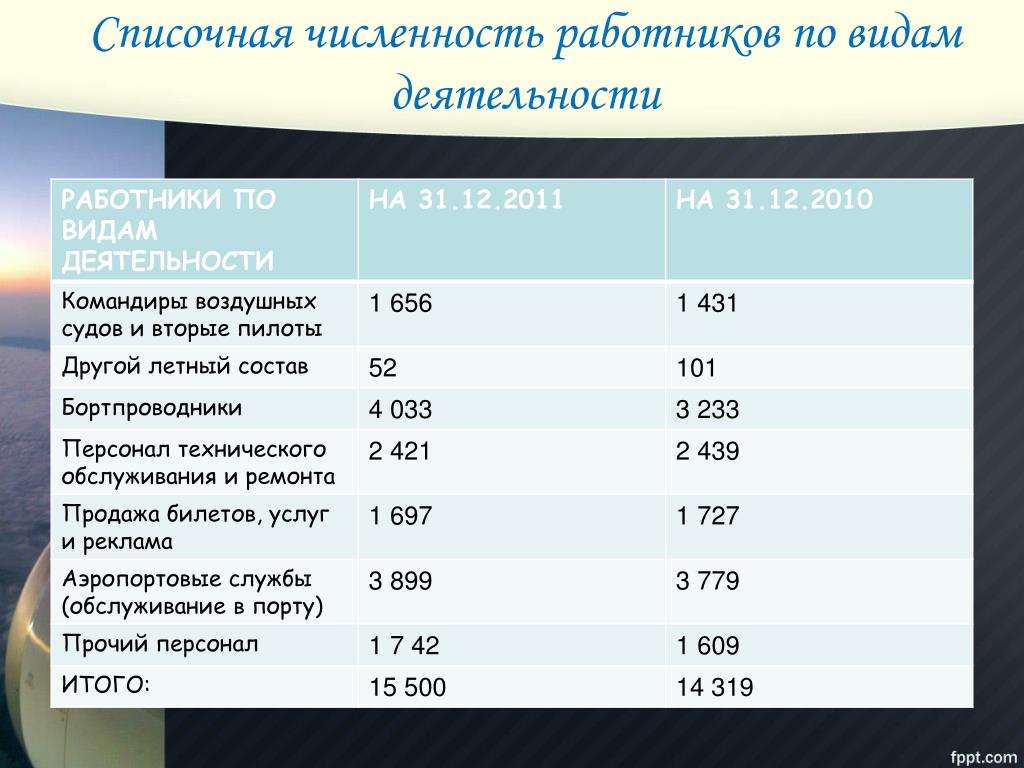

В выходные и праздники в расчет принимается то количество работников, которое было в предшествующий рабочий день. Те сотрудники, которые находятся на больничном или в командировке также включаются в расчет ССЧ работников.

До 21 января года все налогоплательщики должны подать данные о среднесписочной численности за год. Прочитайте, как посчитать среднесписочную численность сотрудников, какие работники включаются в расчет, как учесть работников с неполным рабочим днем. По какой форме надо отчитаться в налоговую.

Расчет среднесписочной численности за 2018 год

Новости Инструменты Форум Барометр. Войти Зарегистрироваться. Вход для зарегистрированных:. Забыли пароль?

ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Как рассчитать среднесписочную численность работников? Часть1. Работники с полной занятостью

Из-за необходимости сдавать отчет ФНС ежегодно, у предпринимателей и юридических лиц нередко возникает вопрос, как рассчитать среднесписочную численность работников за год, какую формулу при этом использовать. Наибольшую сложность вызывают обычно не сами расчеты ССЧ, а то, кого же в это понятие включать. Главный признак — наличие заключенного трудового договора. Но и тут есть свои исключения. Например, работницы, находящиеся в декрете в списочную численность, не включаются. Принцип расчета для разных временных промежутков будет единым.

Среднесписочная численность в 2017 году

Среднесписочная численность работников как рассчитать для ФСС Необходимо сразу отметить, что при заполнении форм все числовые в отчете ФСС-4 сотрудников, работающих на неполном рабочем дне.

Как рассчитать среднесписочную численность работников при неполном рабочем дне?

Виды учета численности работников. Списочное и явочное число работников.

Поможем написать любую работу на аналогичную тему

Получить выполненную работу или консультацию специалиста по вашему учебному проекту

Узнать стоимость

Формирование рабочей силы и рабочего времени на сельскохозяйственных предприятиях зависит от многих условий и факторов:

1. размера, структуры и степени использования земельных угодий;

2. поголовья скота, типа содержания животных;

3. уровня механизации трудовых процессов;

4. территориального размещения производства;

5. степени развитости внутрихозяйственной сети;

6. возможности совмещения профессий;

7. трудоемкости возделывания сельскохозяйственных культур и производства продукции животноводства;

8. наличия в хозяйстве вспомогательных, обслуживающих, перерабатывающих подсобных промышленных производств и промыслов;

9. сезонности использования рабочей силы и целого ряда других.

Для оценки движения рабочей силы используют ряд коэффициентов:

— Коэффициент оборота рабочей силы по приему рассчитывают как отношение числа принятых на работу к среднесписочной численности работников за определенный период.

Коэффициент оборота рабочей силы по выбытию определяется отношением числа уволенных к среднесписочному числу работников за определенный период.

Коэффициент общего оборота рабочей силы представляет собой отношение общего числа принятых и уволенных к среднесписочному числу работников за определенный период.

Коэффициент текучести рабочей силы рассчитывают, как отношение числа выбывших за отчетный период работников по причинам, характеризующим текучесть рабочей силы, к среднесписочной численности за данный период.

Определение потребности в персонале

Норма численности (Нч) – это установленная численность работников определённого профессионально-квалификационного состава, необходимого для выполнения конкретных производственных, управленческих функций или объёмов работ. По нормам численности определяются затраты труда по профессиям, специальностям, группам или видам работ, отдельным функциям, в целом по предприятию, цеху или его структурному подразделению. Численность работников является важнейшим количественным показателем, характеризующим трудовые ресурсы предприятия. Она измеряется такими показателями, как списочная, явочная и среднесписочная численность работников.

Списочная численность (Чсп) работников предприятия — это показатель численности работников списочного состава на определенное число или дату. Она учитывает численность всех работников предприятия, принятых на постоянную, сезонную и временную работу в соответствии с заключенными трудовыми договорами (контрактами), а также работающих собственников организации, получающих в ней заработную плату. Не включаются в списочный состав лица, работающие по договору подряда и другим договорам гражданско-правового характера. В списочном составе работников за каждый календарный день учитываются как фактически явившиеся на работу, так и отсутствующие на работе по каким-либо причинам (отпуска, болезни, командировки и т. д.).

Явочная численность (Чя) характеризует количество работников списочного состава, явившихся на работу в данный день, включая находящихся в командировках. Это необходимая численность рабочих для выполнения производственного сменного задания по выпуску продукции. Разница между явочным и списочным составом характеризует количество отсутствующих по различным причинам (отпуска, болезни и др.). Для приведения явочной численности к списочной используется коэффициент перевода явочной численности рабочих в списочную (Ксп):

В прерывных производствах КСП определяется как отношение табельного (номинального) фонда времени к плановому (эффективному), а в непрерывных — как отношение календарного фонда времени к плановому (эффективному). И, наоборот, для приведения списочного состава к явочному необходимо выполнить следующие расчеты:

Чя = Чсп / Ксп

ИЛИ

Чя = Чсп / (1/ Ксп)

При расчете необходимо помнить, что списочный состав всегда больше явочного состава на количество отсутствующих работников по разным причинам.

Среднесписочная численность — численность работников в среднем за определенный период (месяц, квартал, с начала года, за год). Среднесписочная численность работников за месяц определяется путем суммирования численности работников списочного состава за каждый календарный день месяца. При этом списочная численность работников за выходные и праздничные дни приравнивается к списочной численности персонала предыдущего рабочего дня.

Среднесписочная численность показывает, сколько в среднем работников ежедневно числилось в списках предприятия за рассматриваемый период. При определении среднесписочной численности работники, принятые на неполный рабочий день или неполную рабочую неделю (совместители) учитываются пропорционально фактически отработанному ими времени. Надомники, учитываются как целые единицы. Некоторые работники списочного состава не учитываются при определении среднесписочной численности (женщины, находящиеся в отпусках по беременности и родам, в дополнительном отпуске по уходу за ребенком; работники, находящиеся в учебном отпуске без сохранения заработной платы, и др. ).

Внимание!

Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы.

Расчет среднесписочной численности работников: порядок, формула, примеры

Налоговое законодательство гласит, что индивидуальный предприниматель, которые использовали труд привлеченных специалистов, обязаны рассчитывать и подавать сведения о среднесписочной численности работников (ССЧР). Сведения запрашивают пенсионный фонд, ФСС и налоговая служба. Для расчета отчетности сведений о среднесписочной численности работников существуют определенные правила и формулы.

Правила расчета среднесписочной численности работников

Показатель ССЧР (расчет среднесписочной численности работников) для статистики оформляется на специальном учетном бланке по форме КНД-1110018. Его следует направлять в налоговую инспекцию за год не позднее 20 января с целью определения льготного режима налогообложения и контроля страховых выплат.

С 2014 года от подачи декларации о ССЧР освобождены только те индивидуальные предприниматели, которые не привлекали на работу сотрудников вообще.
Важно помнить, что юридические лица, находящиеся в стадии реорганизации, вновь созданные или действующие не весь год, не освобождаются от расчета показателя.

Для исчисления данного показателя следует учитывать всех сотрудников, которые привлекались по найму временно или постоянно, пребывали в командировке, на бюллетене, в отпуске. Исключение составляют такие категории:

работающие по совместительству из других учреждений;
трудящиеся по договору ГПХ;
работающие по переводу в другой стране или организации;
работающие по ученическому договору с получением стипендиальных выплат;
находящиеся в учебном отпуске без сохранения зарплаты;
женщины, осуществляющие уход за ребенком, или декретном отпуске;
руководители самой организации, которые не получают зарплату;
те, кто написал заявление об увольнении и перестал ходить на работу, не дождавшись официального расторжения трудовых отношений.

Чтобы не допустить погрешностей при исчислении, необходимо использовать первичную документацию по учету сотрудников.

Далее мы подготовили для вас примеры-образцы расчета среднесписочной численности работников за месяц, год по спец. формуле.

Об особенностях расчета среднесписочной численности работников расскажет специалист в видео ниже:

Формула подсчета и примеры

Чтобы вычислить среднесписочную численность работников, необходимо сложить ежедневную численность сотрудников за весь месяц и разделить на число дней в месяце.

ССЧР может рассчитываться за месяц, квартал или год. В двух последних случаях показатель делится на количество месяцев – 3 или 12.
Показатель ССЧР следует округлять до целого числа по общим математическим правилам.

Ниже приведена методика расчета среднесписочной численности работников за квартал.

За квартал

В январе в организации работали 5 человек, в феврале – 8, в марте – 6. Показатель рассчитывается следующим образом: (5+8+6):3=6,33…3. Полученную цифру следует округлить по правилам математики, получается 6.

Ниже приведен порядок расчета среднесписочной численности работников за месяц.

О том, каких работников надо учитывать для расчета среднесписочной численности, расскажет данный видеоролик:

За месяц

По состоянию на 1 марта в учреждении трудились 10 человек, 10 марта работодатель принял на работу еще 9 сотрудников, а 29 марта 4 человека уволились. ССЧР исчисляется следующим образом: (10х9 + (10+9)х19 + (19-4)х3):31=(90+361+45):31=16.

Нюансы при вычислении

Если организация действовала не весь календарный год, а подает данные в налоговую службу за годовой период, то при расчете все равно необходимо делить суммированное число сотрудников на 12 месяцев.
Такая же ситуация при подаче сведений за неполный месяц: сумму делят на количество дней полного месяца.
Если предприятие реорганизуется на основе другой фирмы или ее подразделения, если имеет место перерегистрация юридического лица, то для вычисления ССЧР учитываются календарные дни предшественника.

Для облегчения бухгалтерского труда по учету сотрудников целесообразно применять специализированное программное средство, которое самостоятельно осуществляет расчет ССЧР на основе введенных показателей. Так, например, подобные программы можно скачать в Сети. Также здесь вы можете найти специальные таблицы и онлайн-калькуляторы расчета среднесписочной численности работников за месяц, квартал или год.

О том, как правильно рассчитать среднесписочную численность работников, расскажет это видео:

Как найти среднее значение

Обновлено 21 декабря 2020 г.

Лиза Мэлони

В математике то, что люди обычно называют «средним», правильно известно как «среднее» или «среднее число». На самом деле существует два других типа средних — «режим» и «медиана», о которых вы узнаете, изучая статистику. Но для большинства математических приложений термин «среднее» говорит вам искать среднее значение, которое можно вычислить с помощью базового сложения и деления.

TL; DR (слишком долго; не читал)

Чтобы вычислить среднее значение, сложите все термины, а затем разделите их на количество добавленных терминов. Результат — (среднее) среднее значение.

Как и зачем рассчитывать среднее значение

Что значит рассчитывать среднее или среднее значение? Технически вы делите сумму значений, с которыми работаете, на количество (или количество) чисел в этом наборе. Но в реальном мире это больше похоже на равномерное распределение значения всего набора между каждым из его чисел, а затем отступление назад, чтобы увидеть, к какому значению все числа пришли.

Этот тип среднего полезен для понимания больших наборов данных или оценки положения всей группы. Например, вас могут попросить рассчитать среднюю процентную оценку в вашем классе, средний балл успеваемости среди ваших сокурсников, среднюю зарплату на определенной работе, среднее количество времени, которое требуется, чтобы дойти до автобусной остановки и так далее.

Примеры формулы среднего значения

Имеет ли смысл идея о том, как найти средние значения? Формулу немного неудобно описать словами, но работа над несколькими примерами поможет понять суть.

Пример 1: Найдите среднюю оценку в своем классе математики. Всего 10 студентов, и пока их совокупные оценки в процентах составляют: 77, 62, 89, 95, 88, 74, 82, 93, 79 и 82.

Начните с сложения всех оценок студентов:

77 + 62 + 89 + 95 + 88 + 74 + 82 + 93 + 79 + 82 = 821

Затем разделите полученную сумму на количество добавленных вами баллов. (Вы можете пересчитать их или просто отметить, что исходная задача говорит, что их 10.)

\ frac {821} {10} = 82,1

Результат 82,1 — средний балл в вашем классе математики.

Пример 2: Какое среднее значение для 2, 4, 6, 9, 21, 13, 5 и 12?

Вам не говорят, в каком реальном контексте могут существовать эти числа, но это нормально. Вы по-прежнему можете выполнять математические операции, чтобы найти их среднее значение. Начните с их сложения:

2 + 4 + 6 + 9 + 21 + 13 + 5 + 12 = 72

Затем подсчитайте, сколько чисел вы сложили вместе.Их восемь, поэтому следующий шаг — разделить общую сумму (72) на количество задействованных чисел (8):

\ frac {72} {8} = 9

Таким образом, среднее значение этого набора данных равно 9.

Пример 3: Из учеников вашего класса семеро ездят на автобусе в школу и обратно. (Других водят родители.) В общей сложности эти семь учеников тратят в общей сложности 93 минуты пешком до автобуса и обратно каждый день. Какое среднее время ходьбы ученики вашего класса?

Обычно первым шагом является сложение времени прогулки всех студентов, но это уже было сделано за вас; проблема говорит вам, что общее время их прогулки составляет 93 минуты.

Задача также сообщает вам, со сколькими частями данных вы имеете дело (семь — по одному на каждого учащегося). Итак, если вы внимательно прочитали задачу, все, что вам осталось сделать, чтобы найти среднее, — это разделить сумму или общее количество данных (93 минуты) на количество точек данных (7):

\ frac {93 \ text { минут}} {7} = 13,2857 \ text {minutes}

Большинство людей не заботится о том, прошли ли вы 13,2857 минут или 13,2858 минут, поэтому в таком случае вы почти всегда округлите свой ответ, чтобы получить его. полезнее.

Если округление разрешено, ваш учитель скажет вам, до какого десятичного знака следует округлять. В этом случае давайте округлим до десятых, то есть на одну позицию справа от десятичной дроби. Поскольку число в следующем разряде (разряде сотых) больше 5, вы округлите число в разряде десятых до при усечении десятичной дроби.

Итак, ваш ответ, округленный до десятых, — 13,3 минуты.

Среднее значение, медиана, мода и диапазон

Purplemath

Среднее, медиана и мода — это три вида «средних».В статистике есть много «средних», но я думаю, что это три наиболее распространенных, и, безусловно, те три, с которыми вы, скорее всего, столкнетесь на курсах, предшествующих статистике, если эта тема вообще возникнет.

«Среднее» — это «среднее», к которому вы привыкли, когда вы складываете все числа, а затем делите их на количество чисел. «Медиана» — это «среднее» значение в списке чисел. Чтобы найти медиану, ваши числа должны быть перечислены в числовом порядке от наименьшего к наибольшему, поэтому вам, возможно, придется переписать свой список, прежде чем вы сможете найти медиану. «Режим» — это значение, которое встречается чаще всего. Если ни один номер в списке не повторяется, то для списка нет режима.

MathHelp.com

«Диапазон» списка чисел — это просто разница между наибольшим и наименьшим значениями.

Найдите среднее значение, медианное значение, режим и диапазон для следующего списка значений:

13, 18, 13, 14, 13, 16, 14, 21, 13

Среднее значение — это обычное среднее значение, поэтому я сложу, а затем разделю:

(13 + 18 + 13 + 14 + 13 + 16 + 14 + 21 + 13) ÷ 9 = 15

Обратите внимание, что в данном случае среднее значение не является значением из исходного списка.Это обычный результат. Вы не должны предполагать, что ваше среднее значение будет одним из ваших исходных чисел.

Медиана — это среднее значение, поэтому сначала мне придется переписать список в числовом порядке:

13, 13, 13, 13, 14, 14, 16, 18, 21

В списке девять чисел, поэтому средним будет (9 + 1) ÷ 2 = 10 ÷ 2 = 5-е число:

13, 13, 13, 13, 14, 14, 16, 18, 21

Итак, медиана равна 14.

Режим — это число, которое повторяется чаще, чем любое другое, поэтому 13 — это режим.

Наибольшее значение в списке — 21, наименьшее — 13, поэтому диапазон составляет 21–13 = 8.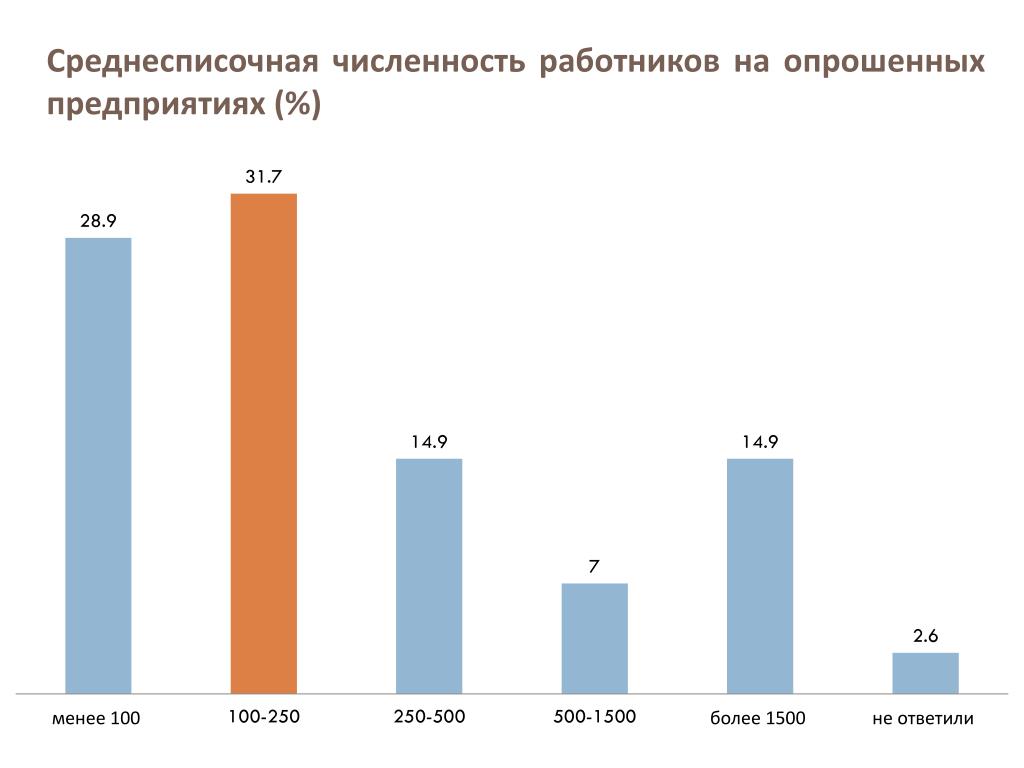

означает: 15
медиана: 14
режим: 13
диапазон: 8

Примечание. Формула для места для нахождения медианы: «([количество точек данных] + 1) ÷ 2», но вам необязательно использовать эту формулу.Вы можете просто рассчитывать с обоих концов списка, пока не встретитесь в середине, если хотите, особенно если ваш список короткий. В любом случае будет работать.

Партнер

Найдите среднее значение, медианное значение, режим и диапазон для следующего списка значений:

1, 2, 4, 7

Среднее значение является обычным средним:

(1 + 2 + 4 + 7) ÷ 4 = 14 ÷ 4 = 3.5

Медиана — это среднее число. В этом примере числа уже перечислены в числовом порядке, поэтому мне не нужно переписывать список. Но нет «среднего» числа, потому что есть четное количество чисел. Из-за этого медиана списка будет средним (то есть обычным средним) двух средних значений в списке. Средние два числа — 2 и 4, поэтому:

(2 + 4) ÷ 2 = 6 ÷ 2 = 3

Итак, медиана этого списка равна 3, а значение, которого нет в списке вообще.

Режим — это номер, который повторяется чаще всего, но все числа в этом списке появляются только один раз, поэтому режима нет.

Наибольшее значение в списке — 7, наименьшее — 1, а их разница — 6, поэтому диапазон равен 6.

среднее: 3,5
медиана: 3
режим: нет
диапазон: 6

Все значения в списке выше были целыми числами, но среднее значение в списке было десятичным. Получение десятичного значения для среднего (или для медианы, если у вас четное количество точек данных) совершенно нормально; не округляйте свои ответы, чтобы попытаться сопоставить формат других чисел.

Найдите среднее значение, медианное значение, режим и диапазон для следующего списка значений:

8, 9, 10, 10, 10, 11, 11, 11, 12, 13

Среднее значение является обычным средним, поэтому я сложу и разделю:

(8 + 9 + 10 + 10 + 10 + 11 + 11 + 11 + 12 + 13) ÷ 10 = 105 ÷ 10 = 10.5

Медиана — это среднее значение. В списке из десяти значений это будет (10 + 1) ÷ 2 = 5,5-е значение; формула напоминает мне с этой «точкой пять», что мне нужно усреднить пятое и шестое числа, чтобы найти медиану. Пятое и шестое числа — это последние 10 и первые 11, поэтому:

(10 + 11) ÷ 2 = 21 ÷ 2 = 10,5

Режим — это номер, который повторяется чаще всего. В этом списке два значения, которые повторяются трижды; а именно 10 и 11, каждое повторяется трижды.

Наибольшее значение — 13, наименьшее — 8, поэтому диапазон 13-8 = 5.

среднее: 10,5
медиана: 10,5
режимы: 10 и 11
диапазон: 5

Как видите, два средних значения (в данном случае среднее и медиана) могут иметь одно и то же значение. Но это , а не , как обычно, и вы должны , а не ожидать этого.

Примечание. В зависимости от вашего текста или преподавателя, приведенный выше набор данных может рассматриваться как не имеющий режима, а не как имеющий два режима, поскольку ни один отдельный номер не повторялся чаще, чем любой другой. Я видел книги, в которых говорится об этом; похоже, что нет единого мнения относительно «правильного» определения «режима» в приведенном выше случае. Поэтому, если вы не знаете, как ответить на «режим» в приведенном выше примере, спросите своего инструктора перед следующим тестом .

Единственная сложная часть нахождения среднего, медианного значения и моды — это точное определение того, какое «среднее» является каким. Просто запомните следующее:

означает: обычное значение «среднего»
медиана: среднее значение
режим: чаще всего

(Выше я использовал термин «средний» довольно случайно. Техническое определение того, что мы обычно называем «средним», технически называется «средним арифметическим»: сложение значений и последующее деление на количество значений.Поскольку вам, вероятно, больше знакомо понятие «среднее», чем «мера центральной тенденции», я использовал более удобный термин.)

Учащийся получил следующие оценки на своих тестах: 87, 95, 76 и 88. Он хочет получить в целом 85 или лучше. Какую минимальную оценку он должен получить за последний тест, чтобы достичь этого среднего?

Минимальная оценка — это то, что мне нужно найти.Чтобы найти среднее значение всех его оценок (известных и неизвестных), мне нужно сложить все оценки, а затем разделить их на количество оценок. Поскольку у меня еще нет оценок за последний тест, я буду использовать переменную для обозначения этого неизвестного значения: « x ». Затем вычисление для нахождения желаемого среднего:

(87 + 95 + 76 + 88 + x ) ÷ 5 = 85

Умножая на 5 и упрощая, получаем:

87 + 95 + 76 + 88 + x = 425

346 + х = 425

x = 79

Ему нужно набрать не менее 79 баллов на последнем тесте.

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в поиске медианы. Попробуйте выполнить указанное упражнение или введите свое собственное. Или попробуйте ввести любой список чисел, а затем выбрать вариант — среднее, медианное, режим и т. Д. — из того, что предлагает вам виджет. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway.

(Щелкните здесь, чтобы перейти непосредственно на сайт Mathway, если вы хотите проверить их программное обеспечение или получить дополнительную информацию.)

URL: https://www.purplemath.com/modules/meanmode.htm

Поиск среднего

Найти среднее или среднее значение — очень простая концепция. Если у вас есть набор чисел, среднее значение определяется путем сложения всех чисел в наборе и деления их суммы на общее количество чисел, добавленных в набор.

Мы можем обобщить понятие среднего с помощью следующей формулы:

Пусть x ₁, x ₂, x ₃, ……, x _n будет набором чисел, среднее значение = (x ₁ + x ₂ + x ₃, + …… + x _n) / n

Проиллюстрируем на примерах:

Пример № 1:

Получите среднее значение следующего набора чисел:

5,4,12,2,1,6

Шаг 1:

Найти сумма:

Сумма = 5 + 4 + 12 + 2 + 1 + 6 = 30

Шаг 2:

Разделить 30 на 6 (общее количество чисел)

30, разделенное на 6, равно 5, поэтому среднее значение равно 5

Пример 2:

Получите среднее значение следующего набора чисел:

5,10,20,5,10

Найдите сумма:

Сумма = 5 + 10 + 20 + 5 + 10 = 50

Разделите 50 на 5 (общее количество добавленных чисел)

50 разделить на 5 равно 10, поэтому 10 — это среднее или среднее значение.

Нахождение среднего, когда числа в наборе совпадают.

Когда все числа в наборе одинаковы, легко найти среднее значение.

Пример № 3

Найдите среднее значение следующего набора чисел:

6, 6, 6

6 + 6 + 6 = 18

18/3 = 6

Пример № 4

Найдите среднее значение следующего набора чисел:

12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12

12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 = 132

132/11 = 12

Что мы можем сделать из примера №3 и примера №4?

Когда все числа в наборе одинаковы, среднее значение — это просто само число.

Нахождение среднего, когда некоторые числа в наборе отрицательные.

Пример № 5

-5, 2, -1, 8

-5 + 2 + -1 + 8 = 4

4/4 = 1

Пример № 6

-8, 2 , -11, 3, 0, 2

-8 + 2 + -11 + 3 + 0 + 2 = -12

-12/6 = -2

Пример № 7:

Г-н Питер собрал 125 карандашей от студентов за последние 5 дней. В среднем, сколько карандашей он собирал каждый день?

Среднее значение = 125/5 = 25

Пример № 8:

На прошлой неделе Сэмюэл заказывал пиццу каждый день.Собрав все свои квитанции и получив общую сумму, он понял, что в общей сложности потратил на пиццу 63 доллара. Сколько в среднем денег он тратил на пиццу каждый день?

Среднее значение = 63/7 = 9

Все еще боретесь с дробями? Избавьтесь от своих страхов и разочарований раз и навсегда!

Купи мою электронную книгу. Он предлагает полный охват фракций!

Веселые математические головоломки
11 марта, 21 06:50
Множество забавных математических головоломок, которые дразнят ваш мозг и оттачивают ваши базовые математические навыки.
Подробнее

Новые уроки математики

Ваша электронная почта в безопасности. Мы будем использовать его только для информирования вас о новых уроках математики.

Среднее арифметическое из 11 чисел в списке равно 14. Если • PrepScholar GRE

Среднее арифметическое значение 11 долларов в списке составляет 14 долларов. Если среднее значение 9 долларов для чисел в списке равно 9 долларам, каково среднее значение для остальных 2-х долларов?

Итак, вы пытались хорошо сдать экзамены и практиковаться в GRE с помощью PowerPrep online.Но тогда у вас возникло несколько вопросов о количественном разделе — в частности, вопрос 20 второго количественного раздела практического теста 1. Эти вопросы, проверяющие наши знания о числовых методах описания данных , могут быть довольно сложными, но не бойтесь, у PrepScholar есть твоя спина!

Изучите вопрос

Давайте поищем в проблеме ключи к разгадке того, что она будет тестировать, поскольку это поможет нам задуматься о том, какие математические знания мы будем использовать для решения этого вопроса.Обращайте внимание на любые слова, которые имеют отношение к математике и что-нибудь особенное в том, как выглядят числа, и отметьте их на нашей бумаге.

Вопрос вращается вокруг среднего списка чисел, поэтому он, вероятно, проверяет наши математические навыки числовых методов описания данных . Давайте вспомним, что мы узнали об этом навыке, когда мы подойдем к этому вопросу.

Что мы знаем?

Давайте внимательно прочитаем вопрос и составим список того, что мы знаем.

Среднее число 11 долларов США составляет 14
Среднее значение 9 долларов из этих чисел составляет 9 долларов
Мы хотим знать среднее значение других чисел $ 2

Разработка плана

Вопрос касается средних значений, поэтому давайте начнем с того, что вспомним наше уравнение для вычисления среднего числа группы чисел.

$$ \ Average = {\ Sum \ of \ Values} / {\ Number \ of \ Values} $$

Так, например, если сумма 10-долларовых чисел составляет 200 долларов, то среднее значение этих 10-долларовых чисел составляет 200/10 долларов, или 20 долларов.С другой стороны, если среднее значение 10 долларов США составляет 20 долларов США, то сумма этих 10 долларов США составляет 200 долларов США. Мы должны сохранять гибкость, когда дело касается сумм и средних значений. С некоторыми вопросами будет проще работать с суммами, а с другими — со средними значениями .

Вопросы, которые дают нам среднее значение набора чисел и среднее значение подмножества большего набора чисел, как правило, легче решать, если мы думаем о суммах, а не о средних для этих чисел.Здесь мы знаем, что если у нас есть сумма «других чисел $ 2 $», то мы могли бы просто разделить эту сумму на 2 $, чтобы получить среднее значение этих 2 $ чисел. И если мы присмотримся, у нас достаточно информации, чтобы вычислить сумму других чисел в $ 2 $, так как:

$$ \ Sum \ of 9 \ Numbers + \ Sum \ of \ Other 2 \ Numbers = \ Sum \ of 11 \ Numbers $$

Из нашего уравнения с суммой и средним мы знаем, что сумма набора чисел — это количество значений, умноженное на среднее. Итак, получаем:

$$ \ Sum \ of 9 \ Numbers = \; 9 · 9 \; \; = 81 $$
$$ \; \ Sum \ of 11 \ Numbers = 11 · 14 = 154 $$

Давайте используем эти две суммы, чтобы найти сумму, а затем среднее значение других чисел в $ 2 $.

Решить вопрос

Таким образом, если сумма всех чисел $ 11 $ составляет 154 $, а сумма 9 $ чисел составляет 81 $, тогда сумма других чисел $ 2 $ должна составлять разницу между этими двумя суммами:

$$ \ Sum \ of \ Other 2 \ Numbers = 154-81 = 73 $$

И если сумма двух чисел составляет 73 доллара, то их среднее значение должно быть 73 доллара / 2 = 36,5 доллара. Итак, правильный ответ — 36,5 $ $.

Что мы узнали

В вопросах, связанных со средними значениями, нам нужно сохранять гибкость.Существует большая вероятность того, что вопрос будет легче решить, если мы переведем средние значения в суммы. Давайте помнить, что только потому, что вопрос сформулирован определенным образом, это не ограничивает нас только способностью думать о вопросе таким образом.

Хотите более квалифицированную подготовку к GRE? Подпишитесь на пятидневную бесплатную пробную версию нашей онлайн-программы PrepScholar GRE, чтобы получить доступ к своему индивидуальному плану обучения с 90 интерактивными уроками и более 1600 вопросами GRE.

Есть вопросы? Оставьте комментарий или отправьте нам письмо по адресу [электронная почта защищена].

Калькулятор статистического среднего для среднего, медианы, режима и диапазона

Пример набора данных

Чтобы показать, как рассчитать среднее, медианное значение, режим и диапазон, я буду использовать следующий набор данных:

36, 3, 8 , 12, 15, 18, 22, 34, 8, 25, 17, 13, 23

Как рассчитать среднее значение?

Среднее значение — это среднее значение всех чисел в наборе данных.Чтобы вычислить среднее значение набора чисел, вы складываете все числа вместе, а затем делите эту сумму на количество элементов в наборе.

Набор данных: 36, 3, 8, 12, 15, 18, 22, 34, 8, 25, 17, 13, 23

Набор данных содержит 13 чисел

Среднее = (36 + 3 + 8 + 12 + 15 + 18 + 22 + 34 + 8 + 25 + 17 + 13 + 23) ÷ 13

Среднее = 234 ÷ 13

Среднее = 18

Как сделать Вы вычисляете медиану?

Медиана — это среднее число в наборе данных после сортировки набора данных от наименьшего к наибольшему.Чтобы вычислить медиану набора данных, вы подсчитываете количество элементов, а затем сортируете элементы от наименьшего к наибольшему. Затем, для нечетного количества элементов , вы добавляете 1 к количеству элементов, а затем делите на 2, чтобы получить позицию среднего числа. В нашем примере набора данных медиана — это 7-е число в отсортированном списке, то есть число 17.

9024

9028 9

Набор данных с нечетными номерами: 36, 3, 8, 12, 15, 18, 22, 34, 8 , 25, 17, 13, 23
Количество элементов в наборе 13
Среднее положение = ((count + 1) ÷ 2)
Среднее положение = ((13 + 1) ÷ 2 )
Среднее положение = (14 ÷ 2)
Среднее положение = 7
Счетчик	1	2	3	4	5	6	8	9	10	11	12	13
Набор данных	3	8	8	12	13				22	23	25	34	36
Медиана = 17 (7-е число в отсортированном наборе данных)

Обратите внимание, что для числа элементов даже вы найдете среднее из двух средних чисел.Первая средняя позиция будет равна количеству элементов, разделенных на 2 минус 1. Вторая средняя позиция будет первой средней позицией плюс 1. Затем вы складываете два средних числа вместе и делите на 2, чтобы найти среднее. Из нашего измененного набора данных примера это дает вам среднее значение 16, что является средним значением для 6-го и 7-го элементов (15 и 17).

Набор данных с четными номерами: 36, 3, 8, 12, 15, 18, 22, 34, 8, 25, 17, 13
Количество элементов в наборе: 12
1-й средний Позиция = (count ÷ 2) — 1
1-я средняя позиция = (12 ÷ 2) — 1 = 6
1-я средняя позиция = 15
2-я средняя позиция = 1-я средняя позиция + 1
2-я средняя позиция = 6 + 1 = 7
2-я средняя позиция = 17
Среднее значение средних чисел = (15 + 17) ÷ 2 = 16
Счетчик	1	2	3	4	5	6	7	8	9	10	11	12
Набор данных											12	13	15	9 0023 17	18	22	25	34	36
Медиана = 16 (среднее 15 и 17)

Как рассчитать режим?

Режим — это номер в наборе данных, который наиболее часто повторяется в наборе.Чтобы найти режим, вы просто подсчитываете, сколько раз каждый уникальный номер появляется в наборе данных. Чаще всего появляется номер режима. В нашем примере набора данных чаще всего встречается номер 8. Следовательно, режим набора данных — 8.

Пример набора данных: 36, 3, 8, 12, 15, 18, 22, 34 , 8, 25, 17, 13, 23
Сортированный набор данных	3	8	8	12	13	15	17	18	23	25	34	36
Режим = 8 (8 встречается чаще всего)

Обратите внимание, что набор данных может иметь более одного режима.Например, если вышеупомянутый набор данных включает еще 3, тогда набор будет иметь два режима: 3 и 8. Набор данных, имеющий два режима, называется бимодальным набором , тогда как набор данных, имеющий более двух режимов, называется называется мультимодальным набором .

Как рассчитать диапазон?

Диапазон — это разница между наибольшим числом в наборе и наименьшим числом в наборе. Чтобы найти диапазон, вы сортируете его от наименьшего к наибольшему, чтобы определить минимальное и максимальное значения.Затем вы вычитаете минимальное значение из максимального, чтобы найти диапазон. В нашем примере установлено минимальное значение 3, а максимальное — 36, в результате получается диапазон 33 (36 — 3).

Пример набора данных: 36, 3, 8, 12, 15, 18, 22, 34, 8, 25, 17, 13, 23
Сортированный набор данных	3	8	8	12	13	15	17	18	22	23	25	34	36
Диапазон = 33 (минимальная разница между 3)

Ошибка средних

Рассмотрим случай со статистиком, который тонет при переходе вброд реки, глубина которой, по его расчетам, составляет в среднем три фута.Если бы он был жив, чтобы рассказать эту историю, он бы разъяснил «недостаток средних значений», который просто утверждает, что планы, основанные на предположениях о средних условиях, обычно ошибаются. Этот основной, но почти всегда невидимый недостаток проявляется повсюду в бизнесе, искажая счета, подрывая прогнозы и обрекая, по-видимому, хорошо продуманные проекты на неутешительные результаты.

Допустим, компания, которую я назову HealthCeuticals, продает скоропортящиеся антибиотики. Хотя спрос на препарат варьируется, в течение многих лет среднемесячный спрос составлял 5000 единиц, так что это количество, которое компания в настоящее время хранит в наличии.Однажды появляется босс. «Дайте мне прогноз спроса на следующий год», — говорит он своему менеджеру по продукту. «Мне это нужно, чтобы оценить инвентарную стоимость для бюджета». Менеджер по продукту отвечает: «Спрос меняется от месяца к месяцу. Вот, позвольте мне дать вам раздачу ». Но босс не хочет «раздачи». «Дай мне номер!» он настаивает. «Что ж, — смиренно говорит менеджер, — средний спрос составляет 5 000 единиц в месяц. Так что, если вам нужно одно число, используйте 5000 ».

Начальник переходит к оценке затрат на товарно-материальные запасы, которые рассчитываются следующим образом: если ежемесячный спрос меньше, чем объем запасов, фирма несет расходы на порчу в размере 50 долларов за непроданную единицу.С другой стороны, если спрос превышает объем запасов, фирма должна доставить дополнительные единицы по воздуху по повышенной стоимости на 150 долларов каждая. Это единственные две затраты, которые зависят от точности прогноза. Босс разработал модель электронной таблицы для расчета затрат, связанных с любым заданным спросом и объемом запасов. Поскольку средний спрос составляет 5000 единиц, он подключает 5000. Поскольку компания всегда хранит в наличии 5 000 единиц, таблица своевременно сообщает, что для этого среднего спроса стоимость равна нулю: нет затрат на порчу или авиаперевозку.

Чистая прибыль, основанная на средних предположениях, должна быть средней чистой прибылью, верно? Он может пропускать колебания от месяца к месяцу, но разве вы не должны, по крайней мере, получить правильную среднюю стоимость, подключив средний спрос? Нет. Легко понять, что средняя стоимость не может быть нулевой, если заметить, что когда спрос на антибиотики HealthCeuticals отклоняется вверх или вниз от среднего значения, компания несет расходы.

Покажи мне номер

О желании руководителей работать с «числом», чтобы ввести среднюю цифру, ходят легенды.Но всякий раз, когда среднее значение используется для представления неопределенной величины, оно приводит к искажению результатов, поскольку игнорирует влияние неизбежных изменений. Средние показатели обычно сводят на нет бухгалтерский учет, инвестиции, продажи, планирование производства и даже прогноз погоды. Даже Общепринятые принципы бухгалтерского учета санкционируют «изъян», требуя, чтобы неопределенности, такие как безнадежная задолженность, вводились едиными цифрами. (К чести, SEC предложила новые правила, которые позволят начать решение этой проблемы.)

В одном знаменитом деле из реальной жизни, когда средние показатели привели к банкротству округа Ориндж, штат Калифорния. Летом 1994 года процентные ставки были низкими, и ожидалось, что они так и останутся. Официальные лица нарисовали радужную картину финансового портфеля округа, основываясь на этом ожидаемом поведении процентных ставок в будущем. Но если бы они явно рассмотрели хорошо задокументированный диапазон неопределенностей процентной ставки, вместо единственного сценария средней процентной ставки, они бы увидели, что существует 5% -ный шанс потерять 1 миллиард долларов или более — что именно и произошло. .Средние скрывали огромную рискованность своих вложений.

Совсем недавно неспособность оценить недостаток привела к материальному ущербу в Северной Дакоте на сумму 2 миллиарда долларов. В 1997 году Служба погоды США прогнозировала, что высота восходящей реки Ред-Ривер в Северной Дакоте достигнет высоты 49 футов. Чиновники в Гранд-Форкс составили планы управления наводнениями на основе этой единственной цифры, которая представляет собой среднее значение. Фактически, река достигла высоты более 50 футов, прорвав плотины и вызвав наводнение, которое вынудило 50 000 человек покинуть свои дома.

Устранение недостатка

Некоторые руководители уже осознали важность принятия мер по ряду значимых чисел — распределению — а не отдельным значениям, и они нанимают статистиков, которые оценивают распределения всего, от цен на акции до спроса на электроэнергию. Все чаще компании обращаются к программным средствам устранения недостатков. Многие программы теперь моделируют неопределенность, генерируя тысячи возможных значений для данного сценария — по сути, заменяя «снимок» с низким разрешением одного среднего числа подробным «фильмом».«Фильм включает в себя целый ряд возможных значений и вероятностей их появления — частотное распределение.

Самый простой и самый популярный инструмент, называемый имитацией Монте-Карло, был описан Дэвидом Герцем в статье HBR 1964 года и популяризирован в финансовых кругах такими искушенными пользователями, как финансовый директор Merck и исполнительный вице-президент Джуди Левент. Сегодня программное обеспечение для моделирования методом Монте-Карло на основе электронных таблиц широко доступно и используется в самых разных областях, таких как разведка нефти, финансовый инжиниринг, оборона, банковское дело и планирование пенсионного портфеля.Wells Fargo Bank, например, использовал моделирование методом Монте-Карло, чтобы спрогнозировать стоимость предложения клиентам CD с переменной ставкой, доходность которых увеличится, если процентные ставки вырастут. Предыдущая оценка, основанная на данных о процентных ставках за три года 1990-х годов, показала, что стоимость пятилетнего CD составит около 0,10%. Но моделирование методом Монте-Карло, которое объединило данные о процентных ставках с 1965 года с моделями поведения клиентов, показало, что расходы банка могут быть в восемь раз больше. Тревожное открытие побудило банк перенастроить свой CD-продукт, чтобы снизить вероятность неприемлемых затрат в случае повышения процентных ставок.

Если бы одержимый средним босс в HealthCeuticals использовал моделирование методом Монте-Карло, он бы увидел не только то, что средняя стоимость запасов не равна нулю, но и то, что он вообще не должен был складировать 5000 единиц. Для таких руководителей, как он, которые по-прежнему привержены единым ценностям, пора изменить образ мышления. Вместо того, чтобы «Дайте мне номер моего отчета», каждый руководитель должен сказать: «Дайте мне раздачу для моей симуляции».

Версия этой статьи появилась в выпуске Harvard Business Review за ноябрь 2002 г.

Почему нельзя доверять средним значениям (или у большинства людей количество ног больше среднего)

Моя подруга Салли увидела отчет, в котором говорится, что средний доход в ее районе составляет 75 000 долларов. Салли чувствует себя неполноценной, потому что ее доход намного ниже среднего по району. Салли спрашивает соседей об их доходах. Все, кого она спрашивает, говорят, что их заработок также ниже среднего по округу. Они проводят небольшое исследование и выясняют, что 98% их сообщества имеют доходы ниже среднего.

Что ?! Я сказал вам — средним нельзя верить.

Оказывается, 2% соседей Салли имеют доходы астрономически выше среднего, что делает «средний» доход выше, чем у остальных 98%.

Средние значения

хорошо подходят для данных, которые распределены равномерно — данных в форме кривой колокольчика, которую вы, возможно, помните из школы. Но когда данные распределяются асимметрично, все становится сложно.

Возьмем, к примеру, район с населением из десяти человек, где девять из них зарабатывают 100 долларов в год, а один из них зарабатывает 10 000 долларов в год.

Как видите, средний показатель намного выше, чем зарабатывает большинство людей.

В этом примере средний доход на душу населения составляет 1090 долларов (10 000 + (9 * 100)) / 10).

Но на самом деле 90% населения зарабатывают примерно на 90% меньше этого.

Если данные плохо распределены — если людей намного больше только на одной стороне спектра, или если есть действительно большие значения только на одном конце континуума — тогда средним нельзя доверять, потому что они не являются хорошими индикаторами для общего понимания, что это такое.

Вот когда вам следует искать медианное значение .

На самом деле, среднее значение гораздо больше похоже на на среднее значение , чем на среднее значение. Медиана — это то, что вы получите, если выровняете все свои измерения по порядку, от наименьшего к наибольшему, а затем выберете то, что находится в самой середине.

Например, если на вашей улице пять домов, средняя стоимость дома определяется путем сложения всех цен на дома и деления на пять.Но средняя стоимость дома будет равна цене дома прямо посередине, с двумя более дорогими домами на вашей улице и двумя домами меньше.

Таким образом, необычно дорогой дом на вашей улице может привести к тому, что среднее значение будет казаться выше, чем вы ожидаете, но среднее значение может больше соответствовать ожидаемой сумме.

Если дома на вашей улице представляют собой разное сочетание цен с более «нормальным» распределением, то среднее значение и медиана, вероятно, будут ближе друг к другу, чем в нашем первом примере, где только один дом был необычно дорогим.

Но даже на этой более сбалансированной улице медиана дает нам лучшее представление о том, как живет большинство людей в этом районе.

Большинство людей помнят, как узнали что-то обо всем этом на уроках математики в старшей школе. Но если вести себя по поводу того, как дикторы используют этот термин, то единственное неизгладимое впечатление от этого урока — это смутное представление о том, что среднее значение как-то связано с этим местом где-то посередине, а термин «медиана» был забыли совсем.И это недоразумение может быть использовано (намеренно или нет) для искажения статистики и искажения нашего понимания фактов.

Это распространенная ошибка. Но важно помнить следующее: среднее значение не обязательно находится где-то рядом с серединой. Иногда это далеко. Иногда это настолько нетипично, насколько это возможно, и не соответствует ни одной точке данных.

Среднесписочная численность это: Среднесписочная численность работников, как рассчитать ССЧ за год в 2021