Средневзвешенная это: СРЕДНЕВЗВЕШЕННОЕ (СРЕДНЕЕ ЗНАЧЕНИЕ) | это… Что такое СРЕДНЕВЗВЕШЕННОЕ (СРЕДНЕЕ ЗНАЧЕНИЕ)?

Средневзвешенная это: СРЕДНЕВЗВЕШЕННОЕ (СРЕДНЕЕ ЗНАЧЕНИЕ) | это… Что такое СРЕДНЕВЗВЕШЕННОЕ (СРЕДНЕЕ ЗНАЧЕНИЕ)?

Расчет средневзвешенного значения в Excel

5988 08.01.2018 Скачать пример

Основная идея

Предположим, что мы с вами сидим в приемно-экзаменационной комиссии и оцениваем абитуриентов, которые хотят поступить в наш ВУЗ. Оценки по различным предметам у наших кандидатов следующие:

Свободное место, допустим, только одно, и наша задача — выбрать достойного. 

Первое, что обычно приходит в голову — это рассчитать классический средний балл с помощью стандартной функции Excel СРЗНАЧ (AVERAGE).

На первый взгляд кажется, что лучше всех подходит Иван, т.к. у него средний бал максимальный. Но тут мы вовремя вспоминаем, что факультет-то наш называется «Программирование», а у Ивана хорошие оценки только по рисованию, пению и прочей физкультуре, а по математике и информатике как раз не очень.

Возникает вопрос: а как присвоить нашим предметам различную важность (ценность), чтобы учитывать ее при расчете среднего? И вот тут на помощь приходит средневзвешенное значение.

Средневзвешенное — это среднее с учетом различной ценности (веса, важности) каждого из элементов.

В бизнесе средневзвешенное часто используется в таких задачах, как:

• оценка портфеля акций, когда у каждой из них своя ценность/рисковость
• оценка прогресса по проекту, когда у задач не равный вес и важность
• оценка персонала по набору навыков (компетенций) с разной значимостью для требуемой должности
• и т.д.

Расчет средневзвешенного формулами

Добавим к нашей таблице еще один столбец, где укажем некие безразмерные баллы важности каждого предмета по шкале, например, от 0 до 9 при поступлении на наш факультет программирования. Затем расчитаем средневзвешенный бал для каждого абитурента, т.

е. среднее с учетом веса каждого предмета. Нужная нам формула будет выглядеть так:

Функция СУММПРОИЗВ (SUMPRODUCT) попарно перемножает друг на друга ячейки в двух указанных диапазонах — оценки абитурента и вес каждого предмета — а затем суммирует все полученные произведения. Потом полученная сумма делится на сумму всех баллов важности, чтобы усреднить результат. Вот и вся премудрость.

Так что берем Машу, а Иван пусть поступает в институт физкультуры ;)

Расчет средневзвешенного в сводной таблице

Поднимем ставки и усложним задачу. Допустим, что теперь нам нужно подсчитать средневзвешенное, но не в обычной, а в сводной таблице. Предположим, что у нас есть вот такая таблица с данными по продажам:

Обратите внимание, что я преобразовал ее в «умную» таблицу с помощью команды

Главная — Форматировать как таблицу (Home — Format as Table) и дал ей на вкладке Конструктор (Design) имя Data.

Заметьте, что цена на один и тот же товар может различаться. Наша задача: рассчитать средневзвешенные цены для каждого товара. Следуя той же логике, что и в предыдущем пункте, например, для земляники, которая продавалась 3 раза, это должно быть:

=(691*10 + 632*12 + 957*26)/(10+12+26) = 820,33

То есть мы суммируем стоимости всех сделок (цена каждой сделки умножается на количество по сделке) и потом делим получившееся число на общее количество этого товара.

Правда, с реализацией этой нехитрой логики именно в сводной таблице нас ждет небольшой облом. Если вы работали со сводными раньше, то, наверное, помните, что можно легко переключить поле значений сводной в нужную нам функцию, щелкнув по нему правой кнопкой мыши и выбрав команду

Итоги по (Summarize Values By): 

В этом списке есть среднее, но нет средневзвешенного :(

Можно частично решить проблему, если добавить в исходную таблицу вспомогательный столбец, где будет считаться  стоимость каждой сделки:

Теперь можно рядом закинуть в область значений стоимость и количество — и мы получим почти то, что требуется:

Останется поделить одно на другое, но сделать это, вроде бы, простое математическое действие внутри сводной не так просто. Придется либо добавлять в сводную вычисляемое поле (вкладка Анализ — Поля, элементы, наборы — Вычисляемое поле), либо считать обычной формулой в соседних ячейках или привлекать функцию ПОЛУЧИТЬ.ДАННЫЕ.СВОДНОЙ.ТАБЛИЦЫ (GET.PIVOT.DATA)

, о которой я уже писал. А если завтра изменятся размеры сводной (ассортимент товаров), то все эти формулы придется вручную корректировать.

В общем, как-то все неудобно, трудоемко и нагоняет тоску. Да еще и дополнительный столбец в исходных данных нужно руками делать. Но красивое решение есть.

Расчет средневзвешенного в сводной таблице с помощью Power Pivot и языка DAX

Если у вас Excel 2013-2016, то в него встроен супермощный инструмент для анализа данных — надстройка Power Pivot, по сравнению с которой сводные таблицы с их возможностями — как счеты против калькулятора. Если у вас Excel 2010, то эту надстройку можно совершенно бесплатно скачать с сайта Microsoft и тоже себе установить. С помощью Power Pivot расчет средневзвешенного (и других невозможных в обычных сводных штук) очень сильно упрощается.

1. Для начала, загрузим нашу таблицу в Power Pivot. Это можно сделать на вкладке

Power Pivot кнопкой Добавить в модель данных (Add to Data Model). Откроется окно Power Pivot и в нем появится наша таблица.

2. Затем щелкните мышью в строку формул и введите туда формулу для расчета средневзвешенного:

Несколько нюансов по формуле:

• В Power Pivot есть свой встроенный язык с набором функций, инструментов и определенным синтаксисом, который называется DAX. Так что можно сказать, что эта формула — на языке DAX.
• Здесь WA — это название вычисляемого поля (в Power Pivot они еще называются меры), которое вы придумываете сами (я называл WA, имея ввиду Weighted Average — «средневзвешенное» по-английски).
  
• Обратите внимание, что после WA идет не равно, как в обычном Excel, а двоеточие и равно.
• При вводе формулы будут выпадать подсказки — используйте их.
• После завершения ввода формулы нужно нажать Enter, как и в обычном Excel.

3. Теперь строим сводную. Для этого в окне Power Pivot выберите на вкладке Главная — Сводная таблица (Home — Pivot Table). Вы автоматически вернетесь в окно Excel и увидите привычный интерфейс построения сводной таблицы и список полей на панели справа. Осталось закинуть поле Наименование в область строк, а нашу созданную формулой меру WA в область значений — и задача решена:

Вот так — красиво и изящно.

Общая мораль: если вы много и часто работаете со сводными таблицами и вам их возможности «тесноваты» — копайте в сторону Power Pivot и DAX — и будет вам счастье!

Ссылки по теме

• Что умеет функция СУММПРОИЗВ на самом деле
• Зачем нужна функция ПОЛУЧИТЬ.ДАННЫЕ.СВОДНОЙ.ТАБЛИЦЫ
• Настройка вычислений в сводных таблицах

Как рассчитать средневзвешенное значение?

Средневзвешенное значение аналогично среднему арифметическому. В среднем арифметическом каждая точка данных вносит равный вклад в окончательное среднее значение, тогда как в средневзвешенном значении несколько точек данных вносят больший вклад в результирующее среднее значение. Здесь каждая точка данных связана с некоторым весом. В зависимости от весов наблюдений вклад в итоговое среднее варьируется.

Средневзвешенное значение — это статистический метод, который рассчитывается путем умножения веса на связанный с ним количественный результат, а затем сложения всех продуктов вместе. Этот результат делится на сумму всех весов, связанных с наблюдениями, что дает средневзвешенное значение. Если все веса наблюдений одинаковы, то среднее арифметическое равно взвешенному среднему.

Содержание

1. Формула взвешенного среднего
2. Шаги для расчета средневзвешенного значения
3. Примеры вопросов

Рассмотрим точки данных x 1,x 2,x 3,…,x n, которые связаны с весами w 1,w 2,w 3,…,w n, тогда средневзвешенное значение можно вычислить по формуле:

Средневзвешенное значение = ∑_iⁿ₌₁ x_i. w_i/∑_iⁿ₌₁ w_i

=(x₁w₁+x₂w₂+x₃w₃+…+x_nw_n)/(w₁+w₂+w₃+…+w_n)

Шаги для расчета средневзвешенного значения

1. Занесите приведенные данные в таблицу, чтобы упростить расчеты.
2. Найдите w i× x i, умножив каждое число на соответствующий вес.
3. Вычислите сумму всех произведений, рассчитанных на шаге 2, чтобы получить ∑w i× x i.
4. Найдите сумму всех весов, т.е. ∑w i.
5. Разделите общее значение, полученное на шаге 3, ∑w i×x i на значение, полученное на шаге 4, ∑w i, чтобы получить взвешенное среднее значение окончательного результата.

Примеры вопросов

Вопрос 1: Найдите средневзвешенное значение для заданных данных

Ценность	Масса
10	4
5	3
20	2
15	6
8	10

Решение:

Учитывая значения, связанные с весами, вычислите ∑w i x i и ∑w i, чтобы найти средневзвешенное значение.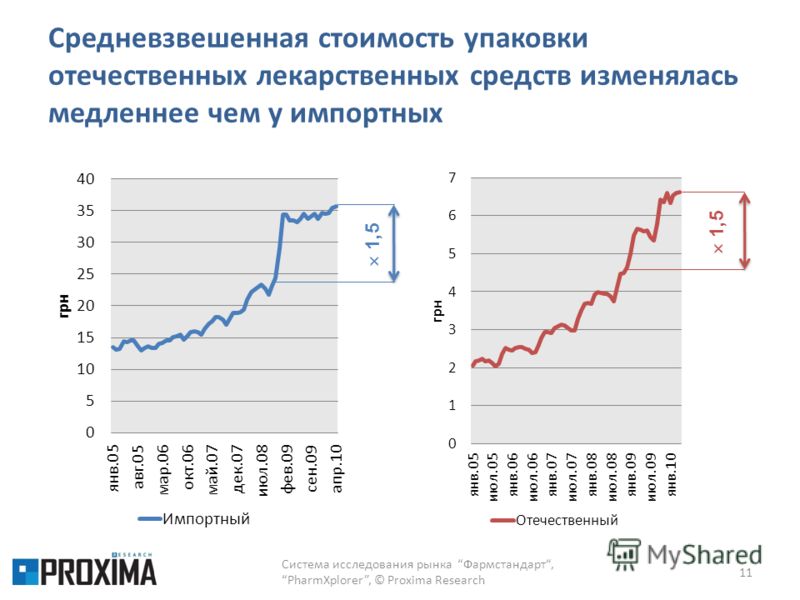

х я	ш я	х я ш я
10	4	40
5	3	15
20	2	40
15	6	90
8	10	80
	∑w я =25	∑w я х я = 265

Средневзвешенное значение = ∑w i x i /∑w i

= 265/25

= 10,6

Средневзвешенное значение для приведенных данных равно 10,6.

Вопрос 2: Найдите средневзвешенное значение для заданных данных

Ценность	Масса
5	5
15	2
25	1

Решение:

Учитывая значения, связанные с весами, вычислите ∑w i x i и ∑w i, чтобы найти средневзвешенное значение.

х я	ш я	х я ш я
5	5	25
15	2	30
25	1	25
	∑w я =8	∑w я х я =80

Средневзвешенное значение = ∑w i x i /∑w i

= 80/8

= 10

Средневзвешенное значение для данных данных равно 10.

Вопрос 3: Найдите средневзвешенное значение для заданных данных

Ценность	Веса
2	4
4	3
6	2
8	1

Решение:

Учитывая значения, связанные с весами, вычислите ∑w i x i и ∑w i, чтобы найти средневзвешенное значение.

х я	ш я	х я ш я
2	4	8
4	3	12
6	5	30
8	1	8
	∑w я =13	∑w я х я = 58

Средневзвешенное значение = ∑w i x i /∑w i

= 58/13

= 4,46

Средневзвешенное значение для приведенных данных равно 4,46.

Вопрос 4: Найдите средневзвешенное значение для заданных данных

Ценность	Масса
80	0,2
90	0,4
70	0,5

Решение:

Учитывая значения, связанные с весами, вычислите ∑w i x i и ∑w i, чтобы найти средневзвешенное значение.

х я	ш я	х я ш я
80	0,2	16
90	0,4	36
70	0,5	35
	∑w i =1,1	∑w я х я =87

Средневзвешенное значение = ∑w i x i /∑w i

= 87/1,1

= 79,09

Средневзвешенное значение для приведенных данных составляет 79,09.

Вопрос 5: Найдите средневзвешенное значение для заданных данных

Ценности	Веса
72	2
66	1
76	1
54	4
62	3

Решение:

Учитывая значения, связанные с весами, вычислите ∑w i x i и ∑w i, чтобы найти средневзвешенное значение.

х я	ш я	х я ш я
72	2	144
66	1	66
76	1	76
54	4	216
62	3	186
	∑w я =11	∑w я х я = 688

Средневзвешенное значение = ∑w i x i /∑w i

= 688/11

= 62,54

Средневзвешенное значение для приведенных данных составляет 62,54.

Средневзвешенное значение: Формула: Как найти средневзвешенное значение





Что такое средневзвешенное значение?

Средневзвешенное значение является разновидностью среднего. Вместо того, чтобы каждая точка данных вносила одинаковый вклад в окончательное среднее значение, некоторые точки данных вносят больший «вес», чем другие. Если все веса равны, то средневзвешенное значение равно среднему арифметическому (обычному «среднему», к которому вы привыкли). Средневзвешенные значения очень распространены в статистике, особенно при изучении населения.

Посмотрите это видео, показывающее, как найти средневзвешенное значение:


Как найти средневзвешенное значение

Посмотрите это видео на YouTube.

Видео не видно? Кликните сюда.

Когда вы найдете «обычное» среднее значение для набора чисел, все числа будут иметь одинаковый вес. Например, если вы хотите найти среднее арифметическое 1, 3, 5, 7 и 10:




1. Сложите точки данных: 1 + 3 + 5 + 7 + 10 = 26.
2. Разделить на количество предметов в наборе: 26 / 5 = 5,2.

Что мы подразумеваем под «равным весом»? Первое предложение в некоторых тестах (например, в этом) иногда звучит так: «Все вопросы имеют одинаковый вес»). Это говорит о том, что все вопросы на экзамене оцениваются одинаково.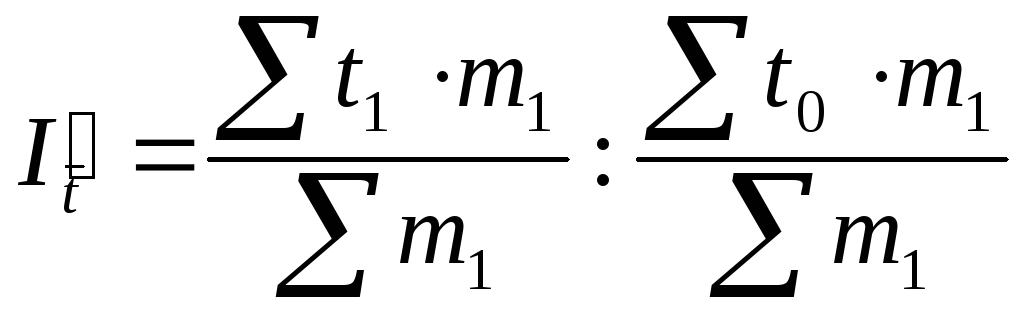 Если у вас есть экзамен на 100 баллов и 10 вопросов, каждый вопрос стоит 1/10 баллов. В приведенном выше вопросе у вас есть набор из пяти чисел. Вы можете думать о том, что каждое число вносит 1/5 в общее среднее значение (поскольку в наборе 5 чисел).

Средневзвешенное значение.

В некоторых случаях может потребоваться, чтобы число имело больший вес. В этом случае вам нужно найти средневзвешенное значение . Чтобы найти средневзвешенное значение:



1. Умножьте числа в вашем наборе данных на веса.
2. Суммируйте результаты.

Для приведенного выше набора чисел с равными весами (1/5 для каждого числа) математика для нахождения средневзвешенного значения будет следующей:
1(*1/5) + 3(*1/5) + 5(* 1/5) + 7(*1/5) + 10(*1/5) = 5,2.

Пример задачи : Вы сдали три 100-балльных экзамена по статистике и набрали 80, 80 и 95 баллов. Последний экзамен намного легче первых двух, поэтому ваш профессор придал ему меньшее значение. Веса для трех экзаменов:

• Экзамен 1: 40 % вашей оценки. (Примечание: 40% в виде десятичной дроби равно 0,4.)
• Экзамен 2: 40 % вашей оценки.
• Экзамен 3: 20 % вашей оценки.

Каково ваше окончательное средневзвешенное значение для класса?

1. Умножьте числа в вашем наборе данных на веса:
   .4(80) = 32
   .4(80) = 32
   .2(95) = 19
2. Сложите числа. 32 + 32 + 19 = 83.

Процент веса, присваиваемый каждому экзамену, называется весовым коэффициентом.

Нужна помощь с домашним заданием? Посетите нашу обучающую страницу!

Формула взвешенного среднего

Средневзвешенное значение найти относительно легко. Но в некоторых случаях сумма весов может не равняться 1. В этих случаях вам нужно будет использовать формулу взвешенного среднего. Единственная разница между формулой и приведенными выше шагами заключается в том, что вы делите на сумму всех весов.

На изображении выше представлена ​​техническая формула для средневзвешенного значения. Проще говоря, формулу можно записать так:
Средневзвешенное значение = Σwx/Σw

• Σ = сумма (другими словами… сложите их!).
• w = веса.
• х = значение.

Чтобы использовать формулу:

1. Умножьте числа в вашем наборе данных на веса.
2. Сложите числа из шага 1 вверх. Отложите этот номер на время.
3. Сложите все веса.
4. Разделите числа, которые вы нашли на шаге 2, на число, которое вы нашли на шаге 3.

В приведенном выше примере задачи с оценками все веса в сумме дают 1 (0,4 + 0,4 + 0,2), поэтому вы должны разделить свой ответ (83) на 1:
83 / 1 = 83.

Однако, скажем, ваши средневзвешенные значения в сумме составляют 1,2 вместо 1. Вы должны разделить 83 на 1,2, чтобы получить:
83 / 1,2 = 69,17.

Предупреждение: На средневзвешенное значение могут легко повлиять выбросы в ваших данных. Если у вас есть очень высокие или очень низкие значения в вашем наборе данных, средневзвешенное значение может быть не очень хорошей статистикой, на которую можно положиться.

Ссылки

Everitt, B. S.; Скрондал, А. (2010), Кембриджский статистический словарь, издательство Кембриджского университета.
Фогт, В.П. (2005). Словарь статистики и методологии: нетехническое руководство по социальным наукам. МУДРЕЦ.

УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Среднее взвешенное: формула: как найти среднее взвешенное» От StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/probability-and-statistics/statistics-definitions/weighted-mean/

————————————————— ————————-

Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!

Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .




Как рассчитать средневзвешенное значение (с примерами) – Zippia

• Как рассчитать средневзвешенное значение
• Как рассчитать средневзвешенное значение из значений больше или меньше 100%
• Примеры расчета средневзвешенного значения
• Как рассчитать средневзвешенное значение в Excel
• Что такое средневзвешенное значение?
• Когда используются средневзвешенные значения?
• Часто задаваемые вопросы по средневзвешенному значению
• Заключительные мысли
• Зарегистрируйтесь для получения дополнительных советов и вакансий

Показать больше

Многие работы в нескольких областях требуют расчета средневзвешенных значений, поскольку они часто дают более точную картину, чем простые средние значения. Важно знать, как рассчитать средневзвешенное значение, и хотя это может показаться сложной задачей, если вы не называете себя математиком, на самом деле это проще, чем вы думаете.

В этой статье вы найдете четкое объяснение и примеры расчета средневзвешенного значения, а также дополнительную информацию о средневзвешенном значении и о том, когда вы будете его использовать.

Основные выводы

• Чтобы вычислить средневзвешенное значение, вы определяете веса каждого значения и складываете их вместе, умножаете каждое значение на его вес, складываете произведения и делите эту сумму на сумму весов.

• Вы можете рассчитать средневзвешенное значение в Excel, используя функции СУММ или СУММПРОИЗВ.

• Средневзвешенные значения часто используются в статистических исследованиях, аудиториях, портфелях акций, измерениях складского веса и учете затрат.

Как вычислить средневзвешенное значение

Чтобы вычислить средневзвешенное значение набора чисел, вы умножаете каждое значение на его вес, а затем добавляете произведения.

Давайте рассмотрим процесс шаг за шагом:

1. Определите веса. В некоторых сценариях определение веса каждого значения довольно просто, хотя и произвольно. Подумайте об учителях, которые предоставляют учебный план, четко определяющий вес различных курсовых работ, составляющих до 100% вашей итоговой оценки.

   В других случаях вес каждого значения рассчитывается математически (ниже мы рассмотрим несколько таких примеров). В биржевой торговле количество акций, которые вы покупаете, представляет собой вес. При работе с массивными наборами статистических данных вес переменной определяется с помощью рандомизированных деревьев данных для обеспечения беспристрастного распределения.

2. Умножьте значение на его вес. После того, как вы определили вес каждого значения, вам нужно просто умножить вес в десятичной форме на значение. Например, если учитель присваивает тестам вес 30 %, вам нужно умножить общий балл за тест на 0,3, чтобы найти среднее значение для этой категории.

3. Добавьте результаты. Чтобы завершить процесс, сложите все взвешенные значения. Число, которое вы получите, выходит за пределы 100, поэтому его можно представить в виде процента или десятичной дроби.

Как рассчитать средневзвешенное значение из значений больше или меньше 100 %

В некоторых случаях невозможно взвесить значения в вашем наборе данных таким образом, чтобы в сумме получилось 100 %. Однако в таких сценариях есть способ определить средневзвешенное значение:

1. Определите веса. Первый шаг в основном такой же, как и в описанном выше процессе, только ваши десятичные разряды не дают в сумме 1. Если вы не хотите вводить систематическую ошибку, вы можете определить частоту, с которой встречается число, а затем сделать это вес переменной, который точно покажет ее влияние на остальную часть набора данных.

   Например, если вы отслеживали свои ежедневные расходы на еду и обнаружили, что:

   • 3 дня вы потратили $15

   • 2 дня вы потратили $35

   • 1 день вы потратили $20

   • 4 дня вы потратили $10

2. Добавьте грузы. Так как ваши веса не складываются автоматически до 1, если вам нужно добавить их самостоятельно. Чтобы продолжить приведенный выше пример, ваша выборка имеет в общей сложности 10 дней, что составляет сумму всех весов.

3. Умножьте каждое значение на его вес. Теперь умножьте каждое значение на его вес. Итак:

   • 3 x 15 долл. США = 45 долл. США

   • 2 x 35 долл. США = 70 долл. США

   • 1 x 20 долларов = 20 долларов

   • 4 x 10 долларов = 40 долларов

4. Суммируйте каждое число, умноженное на его вес. Сложите приведенные выше числа: 45 + 70 + 20 + 40 = 175.

5. Разделить результат на сумму весов.

   Продолжая наш пример, $175 / 10 = $17,5 — это средневзвешенное значение ежедневных расходов на еду.

Примеры расчетов средневзвешенных значений

Здесь мы приведем примеры расчетов средневзвешенных значений с реальными числами, чтобы дать представление о точном процессе.

Несколько примеров будут использовать примеры из реального мира, упомянутые ранее, для обеспечения контекста.

Пример расчета средневзвешенного значения в статистических исследованиях

Исследование проводится для оценки того, отвечают ли мужчины и женщины «ДА» на определенный вопрос.

Предположим, что в итоге участвуют 30 мужчин и 70 женщин.
15 мужчин и 50 женщин ответили «ДА» на вопрос.

Типичный средний расчет показал бы, что (15+50)/100 = 65% мужчин и женщин ответили бы «ДА» на вопрос.

Однако соотношение мужчин и женщин в общей популяции составляет почти ровно 50:50.

Это означает, что женщины перепредставлены в исследовании с коэффициентом 70/50 = 1,4.
Мужчины недопредставлены в исследовании с коэффициентом 50/30 = 1,667.

Таким образом, нормальное среднее значение не является репрезентативным для генеральной совокупности. Нам требуется расчет, учитывающий непропорциональность обследуемых групп.

Именно для этого и используются средневзвешенные значения.

Мы хотим, чтобы ответы мужчин были выше, а ответы женщин — ниже.

Разделите 50 женщин, ответивших «ДА», на весовой коэффициент 1,4 (их фактор чрезмерной представленности).

50/1,4 = 35,71

Умножьте 15 мужчин, ответивших «ДА», на вес 1,667 (их фактор недопредставленности).

15 х 1,667 = 25

Последний шаг — сложить эти два значения и разделить на количество участников исследования, получив средневзвешенное значение.

(35,71 + 25)/100 = 60,71%

Этот средневзвешенный процент 60,71% гораздо более репрезентативен для населения, чем наш обычный средний показатель 65%.

Пример расчета средневзвешенного значения в торговле природным газом

Торговцев природным газом часто интересует средняя цена на газ с поправкой на объем в конкретном регионе.

Обычно в одном регионе много заправок. Каждый из них различается как по цене, так и по объему предложения. Обычный средний расчет бесполезен, поскольку он не учитывает эти разные объемы.

Расчет средневзвешенного значения решает эту проблему. Рассмотрим следующую формулу:

Цена региона = ((Цена Станции 1 x Объем Станции 1) + (Цена Станции 2 x Объем Станции 2) + (Цена Станции 3 x Объем Станции 3) + …) / (Общий объем)

Выше приведена средневзвешенная формула, в которой в качестве значения веса используется объем подачи газа каждой станции. Таким образом, продавец природного газа может получить реальную среднюю цену газа с поправкой на объем.

Давайте теперь воспользуемся действительными числами, чтобы показать различные результаты, полученные при вычислении нормального среднего и средневзвешенного значения.

Цены и объем на каждой станции:

• Станция 1. Цена = 2,15 доллара США и объем = 100 галлонов

• Станция 2. Цена = 2,05 доллара США и объем = 150 галлонов

• Станция 3. Цена = 1,95 доллара США и объем = 50 галлонов

Обычное среднее значение просто усредняет цены трех станций.

Среднее значение = (2,15 + 2,05 + 1,95)/3 = 2,05

Средневзвешенное значение использует объем, поставляемый на каждой станции, в качестве значения веса.

Средневзвешенное значение = ((2,15 x 100) + (2,05 x 150) + (1,95 x 50))/300 = 2,067

Это значение является истинной средней ценой на газ в регионе. Эта разница может иметь решающее значение для успеха или неудачи трейдера.

Пример расчета средневзвешенного значения в классах

Профессора и преподаватели должны понимать средневзвешенные значения, чтобы точно рассчитывать итоговые оценки своих студентов.

Экзамен, домашнее задание и оценки за контрольную редко бывают одинаково важны. Таким образом, необходимо учитывать значения веса, чтобы получить достоверный взгляд на успеваемость учащегося.

Предположим, что оценки учащихся складываются следующим образом:

• экзаменов = 70%

• викторин = 20%

• заданий = 10%

Значения каждой из вышеуказанных категорий могут быть использованы в качестве значений веса.

Вот баллы, которые получили два студента в каждой из категорий:

• Тимми. Экзамены = 50%, тесты = 40% и задания = 70%

• Боб. Экзамены = 76%, тесты = 65% и задания = 12%

Теперь давайте посчитаем их взвешенные оценки.

Взвешенная оценка Тимми = (0,7 x 0,5) + (0,2 x 0,4) + (0,1 x 0,7) = 0,5 = 50%
Взвешенная оценка Боба = (0,7 x 0,76) + (0,2 x 0,65) + (0,1 x 0,12) = 0,674 = 67,4%

Очевидно, что оба ученика должны учиться усерднее.

Пример расчета средневзвешенного значения в повседневной жизни

Вычисление средневзвешенных значений важно не только во многих областях, связанных с математикой и финансами, но и может помочь вам в повседневной жизни.

Предположим, Джон подумывает о покупке нового телефона. Он выбирает следующую систему, чтобы оценить, насколько важны для него определенные функции:

Затем эти оценки можно использовать в качестве весов для расчета средневзвешенной оценки различных моделей телефонов.

Сравнение этих относительных показателей позволяет Джону сравнить телефоны и легко принять решение о покупке.

Предположим, три рассматриваемых им телефона имеют следующие рейтинги:

• Новый айфон. Срок службы батареи = 5, качество изображения камеры = 8 и объем памяти = 7.

• Новый Android. Срок службы батареи = 4, качество изображения камеры = 5 и объем памяти = 3.

• Новый Хуавей. Срок службы батареи = 6, качество изображения камеры = 3 и объем памяти = 6.

Используя относительную важность каждой функции в качестве значения веса, давайте теперь рассчитаем средневзвешенный балл каждой модели телефона.

Новый показатель iPhone = (0,4 x 5) + (0,2 x 8) + (0,4 x 7) = 6,4
Новый показатель Android = (0,4 x 4) + (0,2 x 5) + (0,4 x 3) = 3,8
Новый показатель Оценка Huawei = (0,4 х 6) + (0,2 х 3) + (0,4 х 6) = 5,4

Самый высокий балл у iPhone, так что Джон теперь знает, какой телефон купить.

Как вычислить средневзвешенное значение в Excel

Иногда средневзвешенное значение может быть слишком запутанным для ручки, бумаги и простого калькулятора. И если вы учитель, подсчитывающий оценки для десятков учеников, или финансовый эксперт, анализирующий тысячи точек данных, разумно обратиться к Excel или аналогичному программному обеспечению.

Вот несколько способов найти средневзвешенное значение для набора данных с помощью Excel:

• Использование функции СУММ. Если вы знакомы с основами Excel, у вас, вероятно, есть опыт работы с функцией СУММ, которая просто складывает набор чисел. Более сложная часть заключается в разработке этого набора чисел в первую очередь.

  Для начала поместите значения в один столбец, а веса в другой столбец. Допустим, значения находятся в столбце C, а веса — в столбце D.

  Затем создайте ячейку, посвященную вашему средневзвешенному значению. Затем в этой ячейке введите формулу:

  =СУММ(C2*D2, C3*D3, C4*D4)

  и далее для любого количества строк.

  Наконец, разделите результат на сумму количества значений. В Excel это будет выглядеть как

  .

  /СУММ(Д2:Д6)

  (где цифры «2» и «6» обозначают диапазон значений, включенных в набор данных). Другими словами, вы будете делить на 5 (2, 3, 4, 5, 6).

  В сумме ваша формула будет выглядеть так:

  =СУММ(C2*D2, C3*D3, C4*D4, C5*D5, C6*D6)/СУММ(D2:D6)

  Эта стратегия очень интуитивно понятна, поскольку она аналогична расчету средневзвешенного значения вручную. Точно так же он действительно эффективен только для небольших наборов данных — в противном случае вы захотите перейти ко второму варианту.

• Использование функции СУММПРОИЗВ. Для больших наборов имеет смысл использовать функцию СУММПРОИЗВ. Вместо того, чтобы умножать каждое значение на его вес по отдельности, вы предоставляете целый диапазон ячеек и сообщаете формуле, что одно число является значением, а другое — весом. Эти диапазоны называются «массивами».

  Теперь давайте предположим ту же настройку, что и в приведенном выше примере, со значениями в столбце C и весами в столбце D. Ваша формула будет выглядеть как

  .

  =СУММПРОИЗВ(C2:C6, D2, D6)

  Формула по существу такая же, как и приведенная выше, с тем преимуществом, что вам не нужно вручную вводить ячейки веса и значения; просто перетащите свой диапазон для каждого массива, а формула сделает все остальное.

  Теперь вам просто нужно разделить на сумму всех значений в вашем наборе, как в приведенной выше формуле. Опять же, это выглядит так:

  /СУММ(Д2:Д6)

  Итого, ваша формула:

  =СУММПРОИЗВ(C2:C6, D2, D6)/СУММ(D2:D6)

Обратите внимание, что любой подход будет работать с весами, которые в сумме не составляют 1 или 100%. Ваши результаты также не обязательно должны быть выражены в процентах. Эти простые формулы Excel могут сэкономить вам кучу времени при расчете средневзвешенных значений.

Что такое средневзвешенное значение?

Средневзвешенное значение — это среднее значение набора данных, учитывающее различные степени важности чисел в наборе.

Каждое число в наборе данных умножается на заданное значение веса при расчете средневзвешенного значения.

Для сравнения, обычные расчеты средних значений обрабатывают каждое число в наборе данных так, как если бы им был присвоен одинаковый вес.

Шаг после умножения чисел на веса одинаков как для невзвешенных, так и для взвешенных средних. Каждое число суммируется, а затем делится на количество элементов в наборе.

Использование средневзвешенного значения по сравнению с обычным средним значением может дать совершенно другую картину.

Это верно в таких ситуациях, как расчет пособий, которые получает средний безработный. Только часть безработных может получать пособия.

При расчете средневзвешенного значения это можно легко учесть путем корректировки значений веса для компенсации.

Обычный расчет среднего значения полностью упускает эту деталь или требует больше данных, чтобы обеспечить такой же точный вид.

Когда используются средневзвешенные значения?

Средневзвешенные значения полезны всегда, когда одни значения важнее других. Есть много реальных ситуаций, когда это так.

Понимание средневзвешенных значений будет обязательным навыком, если любая из ваших запланированных работ будет включать следующее:

• Статистические исследования. Предположим, что статистики проводят опрос для оценки мнений мужчин и женщин по определенной теме. Тем не менее, один пол в конечном итоге участвует в исследовании гораздо меньше, чем другой.

  Соотношение полов в общей популяции (почти 50:50) сильно отличается от соотношения в исследовании. Чтобы компенсировать это, исследовательская группа может взвесить ответы каждой гендерной группы, чтобы они были представлены пропорционально.

  Подобные сценарии широко распространены в любой области исследований.

• Классы. Оценка, которую учащийся получает на экзамене, может быть гораздо важнее, чем его оценка за домашнее задание. Таким образом, экзаменационный балл учащегося получает более высокий вес при расчете его оценки за курс.

  Взвешенный средний балл также требует аналогичных расчетов.

• Портфель акций. Инвестор покупает акции компании в течение определенного периода времени. Им может быть сложно отслеживать их среднюю стоимость, поскольку стоимость акций колеблется.

  Они могут решить эту проблему, рассчитав средневзвешенное значение, используя цены, по которым они купили акции, в качестве различных значений веса.

  Средневзвешенные значения широко используются в финансовой сфере, особенно количественными аналитиками. Вам нужно будет рассчитать средневзвешенные значения не только для цен на акции, но и почти для каждого значения в балансе.

• Измерение складского веса. Товары часто хранятся на отдельных поддонах внутри складов. Весовщику или оператору весов может быть поручено собирать точные измерения веса этих предметов.

  Поскольку некоторые лоты могут быть заполнены намного больше, чем другие, простого усреднения веса каждого типа предмета недостаточно.

  Чтобы учесть эти различия, при расчете средневзвешенного значения в качестве значения веса используется количество каждого типа номенклатуры.

• Учет затрат. Предположим, компания заказывает различное количество различных товаров, и их старший бухгалтер пытается рассчитать среднюю стоимость товаров.

  Вместо того, чтобы просто усреднять цену каждого типа товара, необходимо учитывать частоту, с которой каждый из них покупался.

  Расчет средневзвешенного значения может учитывать эти различные частоты как значение веса, обеспечивая более точный расчет средней стоимости.

Средневзвешенные расчеты используются во многих других сферах деятельности, например, специалистами по финансированию и актуариями.

Часто задаваемые вопросы о средневзвешенном значении

1. Чем средневзвешенное значение отличается от простого среднего?

   Средневзвешенное значение отличается от простого среднего тем, что оно учитывает большее значение некоторых усредняемых элементов, в то время как простое среднее рассматривает все элементы так, как будто они имеют одинаковую важность.

   Например, когда вы рассчитываете свою среднюю оценку за класс, балл, который вы получили на выпускном экзамене, как правило, более ценен, чем балл, который вы получили на меньшем тесте, и средневзвешенное значение учитывает это.

2. Для чего в бухгалтерском учете используется средневзвешенное значение?

   Средневзвешенное значение используется для оценки запасов в бухгалтерском учете. Это называется методом средневзвешенной стоимости (WAC), и он учитывает как количество товаров, доступных для продажи, так и их стоимость для расчета WAC за единицу.

3. Зачем использовать средневзвешенное значение вместо традиционного расчета среднего?

   Вы бы использовали средневзвешенное значение вместо традиционного расчета среднего значения, потому что вычисление средневзвешенного значения учитывает различные значения элементов, которые вы усредняете.

   Традиционные расчеты средних значений могут вводить в заблуждение, если они используются для усреднения значений, которые имеют совершенно разные значения или важность.

   Например, будучи студентом, вы не хотите, чтобы плохая оценка, которую вы получили за тест из десяти вопросов, имела такой же вес в итоговой оценке, как и ваш последний проект, над которым вы работали неделями. Расчет средневзвешенного значения гарантирует, что этого не произойдет, поскольку итоговому проекту придается большее значение, чем опросу.

Заключительные мысли

Вычисление средневзвешенного значения дает много преимуществ по сравнению с простым средним значением.

Его используют повсеместно, как в повседневной жизни, так и во многих профессиональных областях.

В условиях такой конкуренции на рынке труда, каждый работающий профессионал должен развивать свои навыки.

Насколько полезен был этот пост?

Нажмите на звездочку, чтобы оценить!

Средний рейтинг / 5.