Ставка дисконтирования при которой npv 0 называется: NPV, NPV, 4.1. , (IRR), . NPV =0 —
Инвестировать — это значит вложить свободные финансовые ресурсы сегодня с целью получения стабильных денежных потоков в будущем. Вкладываться можно в финансовые инструменты, или в новый бизнес, или в расширение уже существующего бизнеса. В любом случае, инвестирование — это вложение денег в какие-то активы на долгосрочную перспективу.
Как не ошибиться и не только вернуть вложенные средства, но еще и получить прибыль от инвестиций?
Для этого можно воспользоваться одним из методов оценки эффективности инвестиционных проектов. NPV — это один из таких методов. Найти NPV инвестиционного проекта означает найти чистую приведенную стоимость всех денежных потоков, связанных с этим проектом.
Как это сделать, используя формулу для расчета NPV, и так ли это сложно, читайте ниже.
Что можно делать с деньгами?
Если у вас появилась некоторая сумма денег, то есть три возможности ими распорядиться:
- а) потратить
- б) спрятать в сейф на «черный день». И всё время трястись, что их украдут. И с грустью наблюдать, как они обесцениваются в результате инфляции
- в) «вложить» (инвестировать) куда-нибудь с целью получения дохода в будущем. А будет ли это выгодно?
Эта статья для тех, кто выбирает третий пункт из этого списка. И не важно, собираетесь ли вы инвестировать свои деньги или деньги компании, в которой вы будете работать финансовым специалистом.
Инвестировать можно в банк, положив деньги на депозит, а можно купить долговые обязательства или акции банков или компаний, которые свободно торгуются на финансовом рынке. Это самый простой путь, но не самый доходный. Для физических лиц, то есть нас с вами, чаще всего, это единственный способ вложения накоплений.
А можно инвестировать в бизнес, что означает купить долгосрочные активы (основные средства), используя которые в процессе производства, торговли или оказания услуг, вы будете получать в будущем притоки денежных средств. Для юридических лиц (компаний) это собственно говоря, и является целью их существования — делать деньги (прибыль) из инвестиций.
Чтобы определить, будет ли успешным тот или иной инвестиционный проект, финансовыми специалистами используются определенные методы оценки проектов. Два основных метода — это NPV и IRR.
NPV — что это такое? Какая логика в этом показателе?
NPV — это сокращение по первым буквам фразы «Net Present Value» и расшифровывается это как чистая приведенная (к сегодняшнему дню) стоимость. Это метод оценки инвестиционных проектов, основанный на методологии дисконтирования денежных потоков.
Если вы знаете перспективный бизнес-проект и хотите вложить в него деньги, то неплохо было бы для начала рассчитать NPV (=чистую приведенную стоимость) этого бизнес-проекта. Алгоритм расчета такой:
- 1) нужно оценить денежные потоки от проекта — первоначальное вложение (отток) денежных средств и ожидаемые поступления (притоки) денежных средств в будущем
- 2) определить стоимость капитала (cost of capital) для вас — это будет ставкой дисконтирования
- 3) продисконтировать все денежные потоки (притоки и оттоки) от проекта по ставке, которую вы оценили в п.2)
- 4) Сложить. Сумма всех дисконтированных потоков и будет равна NPV проекта
Правило: если NPV больше нуля, то проект можно принять, если NPV меньше нуля, то проект стоит отвергнуть.
Логическое обоснование метода NPV очень простое. Если NPV равно нулю, это означает, что денежные потоки от проекта достаточны, чтобы
- а) возместить инвестированный капитал и
- б) обеспечить необходимый доход на этот капитал.
Если NPV положительный, значит, проект принесет прибыль, и чем больше величина NPV, тем выгоднее/прибыльнее является данный проект. Поскольку доход кредиторов (у кого вы брали деньги в долг) фиксирован, весь доход выше этого уровня принадлежит акционерам. Если компания одобрит проект с нулевым NPV, позиция акционеров останется неизменной – компания станет больше, но цена акции не вырастет. Однако, если проект имеет положительную NPV, акционеры станут богаче.
Формула NPV — пример расчета
Формула расчета NPV выглядит сложно на взгляд человека, не относящего себя к математикам:
Где:
- n, t — количество временных периодов,
- CF — денежный поток (Cash Flow),
- R — стоимость капитала (ставка дисконтирования, Rate)
На самом деле эта формула — всего лишь правильное математическое представление суммирования нескольких величин. Чтобы рассчитать NPV, возьмем для примера два проекта А и Б, которые имеют следующую структуру денежных потоков в ближайшие 4 года:
Оба проекта А и Б имеют одинаковые первоначальные инвестиции в 10,000, но денежные потоки в последующие годы сильно разнятся. Проект А предполагает более быструю отдачу от инвестиций, но к четвертому году денежные поступления от проекта сильно упадут. Проект Б, напротив, в первые два года показывает более низкие денежные притоки, чем поступления от Проекта А, но зато в последующие два года Проект Б принесет больше денежных средств, чем проект А.
Рассчитаем NPV инвестиционного проекта следующим образом:
Предположения для упрощения расчета:
- а) все денежные потоки случаются в конце каждого года,
- б) первоначальный денежный отток (вложение денег) произошел в момент времени «ноль», т.е. сейчас
- б) стоимость капитала (ставка дисконтирования) составляет 10%
Про дисконтирование денежных потоков на этом сайте есть отдельная статья. Если расчет, приведенный ниже, вам покажется совсем непонятным, то лучше будет сначала вспомнить основы дисконтирования, вернувшись к этой статье.
Коротко напомню: чтобы привести денежный поток к сегодняшнему дню, нужно умножить денежную сумму на коэффициент 1/(1+R), при этом (1+R) надо возвести в степень, равную количеству лет. Величина этой дроби называется фактором или коэффициентом дисконтирования. Чтобы не вычислять каждый раз этот коэффициент, его можно посмотреть в специальной таблице, которая называется «таблица коэффициентов дисконтирования».
Применим формулу NPV для Проекта А. У нас четыре годовых периода и пять денежных потоков. Первый поток (10,000) — это наша инвестиция в момент времени «ноль», то есть сегодня. Если развернуть формулу NPV, приведенную чуть выше, то мы получим сумму из пяти слагаемых:
Если подставить в эту сумму данные из таблицы для Проекта А вместо CF и ставку 10% вместо R, то получим следующее выражение:
То, что стоит в делителе, можно рассчитать, но проще взять готовое значение из таблицы коэффициентов дисконтирования и умножить эти коэффициенты на сумму денежного потока.
В результате приведенная стоимость денежных потоков (NPV) для проекта А равна 788,2 доллара. Расчет NPV для проекта А можно так же представить в виде таблицы и в виде шкалы времени:
Точно таким же образом рассчитывается NPV для проекта Б.
Поскольку коэффициенты дисконтирования уменьшаются с течением времени, вклад в приведенную стоимость проекта больших (4,000 и 6,000), но отдалённых по времени (третий и четвертый годы) денежных потоков будет меньше, чем вклад от денежных поступлений в первые годы проекта. Поэтому ожидаемо, что для проекта Б чистая приведенная стоимость денежных потоков будет меньше, чем для Проекта А.
У меня получилось, что NPV Проекта Б — 491,5 доллара.
Расчет NPV для проекта Б можно посмотреть в таблице и на рисунке со шкалой времени.
Вывод: оба проекта можно принять, так как NPV обоих проектов больше нуля, а, значит, осуществление этих проектов приведет к увеличению стоимости компании-инвестора.
Если эти проекты взаимоисключающие, то есть необходимо выбрать один из них, то предпочтительнее выглядит Проект А, поскольку его NPV заметно больше 788,2, чем NPV Проекта Б 491,5.
Цифры для расчета NPV инвестиционного проекта — в чём сложность?
Применить математическую формулу несложно, если известны все переменные. Когда у вас есть все цифры — денежные потоки и стоимость капитала — то вы легко сможете подставить их в формулу и рассчитать NPV. Но не всё так просто. Реальная жизнь отличается от чистой математики тем, что невозможно точно определить величину переменных, которые входят в эту формулу. Собственно говоря, именно поэтому на практике примеров неудачных инвестиционных решений гораздо больше, чем удачных.
а) Денежные потоки
Самый важный и самый трудный шаг в анализе инвестиционных проектов — это оценка всех денежных потоков, связанных с проектом. Во-первых, это величина первоначальной инвестиции (оттока средств) сегодня. Во-вторых, это величины годовых притоков и оттоков денежных средств, которые ожидаются в последующие периоды.
Сделать точный прогноз всех расходов и доходов, связанных с большим комплексным проектом, невероятно трудно. Например, если инвестиционный проект связан с выпуском на рынок нового товара, то для расчета NPV необходимо будет сделать прогноз будущих продаж товара в штуках, и оценить цену продажи за единицу товара. Эти прогнозы основываются на оценке общего состояния экономики, эластичности спроса (зависимости уровня спроса от цены товара), потенциального эффекта от рекламы, предпочтений потребителей, а также реакции конкурентов на выход нового продукта.
Кроме того, необходимо будет сделать прогноз операционных расходов (платежей), а для этого оценить будущие цены на сырье, зарплату работников, коммунальные услуги, изменения ставок аренды, тенденции в изменении курсов валют, если какое-то сырье можно приобрести только за границей и так далее. И все эти оценки нужно сделать на несколько лет вперед.
б) Ставка дисконтирования
Ставка дисконтирования в формуле расчета NPV — это стоимость капитала (cost of capital) для инвестора. Другими словами, это ставка процента, по которой компания-инвестор может привлечь финансовые ресурсы.
В общем случае компания может получить финансирование из трех источников:
- взять в долг (обычно у банка)
- продать свои акции
- использовать внутренние ресурсы (нераспределенную прибыль)
ЧИТАЙТЕ ТАКЖЕ: Ставка дисконтирования для инвестиционного проекта. Это WACC — средневзвешенная стоимость капитала
Финансовые ресурсы, которые могут быть получены из этих трех источников, имеют свою стоимость. И она разная! Наиболее понятна стоимость долговых обязательств (пункт 1 списка). Это либо процент по долгосрочным кредитам, который требуют банки, либо процент по долгосрочным облигациям, если компания может выпустить свои долговые инструменты на финансовом рынке. Оценить стоимость финансирования из двух остальных источников сложнее. Финансистами давно разработаны несколько моделей для такой оценки, среди них небезызвестный CAPM (Capital Asset Pricing Model). Но есть и другие подходы.
Стоимость капитала для компании (и, следовательно, ставка дисконтирования в формуле NPV) будет средневзвешенная величина процентных ставок их этих трех источников. В англоязычной финансовой литературе это обозначается как WACC — сокращение по первым буквам английской фразы Weighted Average Cost of Capital, что переводится как средневзвешенная стоимость капитала.
Зависимость NPV проекта от ставки дисконтирования
Понятно, что получить абсолютно точные величины всех денежных потоков проекта и точно определить стоимость капитала, т.е. ставку дисконтирования невозможно. В этой связи интересно проанализировать зависимость NPV от этих величин. У каждого проекта она будет разная. Наиболее часто делается анализ чувствительности показателя NPV от стоимости капитала.
Давайте рассчитаем NPV по проектам А и Б для разных ставок дисконтирования. Я сделала этот расчет в Excele, результаты приведены в таблице ниже:
Табличная форма уступает графической по информативности, поэтому гораздо интереснее посмотреть результаты на графике (нажать, чтобы увеличить изображение):
Из графика видно, что NPV проекта А превышает NPV проекта Б при ставке дисконтирования более 7% (точнее 7,2%). Это означает, что ошибка в оценке стоимости капитала для компании-инвестора может привести к ошибочному решению в плане того, какой проект из двух следует выбрать.
Кроме того, из графика также видно, что Проект Б (красная линия) является более чувствительным в отношении ставки дисконтирования. То есть NPV проекта Б уменьшается ,быстрее по мере роста этой ставки (красный график более крутой). И это легко объяснимо. В проекте Б денежные поступления в первые годы проекта невелики, со временем они увеличиваются. Но коэффициенты дисконтирования для более отдаленных периодов времени уменьшаются очень значительно. Поэтому вклад больших денежных потоков в чистую приведенную стоимость так же резко падает.
Например, можно рассчитать, чему будут равны 10,000 долларов через 1 год, 4 года и 10 лет при ставках дисконтирования 5% и 10%, то наглядно можно увидеть, как сильно зависит приведенная стоимость денежного потока от времени его возникновения:
В последнем столбце таблицы видно, что один и тот же денежный поток (10,000) при разных ставках дисконтирования отличается через год всего на 4.5%. Тогда как тот же самый по величине денежный поток, только через 10 лет от сегодняшнего дня при дисконтировании по ставке 10% будет на 37,2% меньше, чем его же приведенная стоимость при ставке дисконтирования 5%. Высокая стоимость капитала (=ставка дисконтирования) «съедает» существенную часть дохода от инвестиционного проекта в отдаленные годовые периоды, и с этим ничего не поделать. Это математика.
Именно поэтому, при оценке инвестиционных проектов денежные потоки, отстоящие от сегодняшнего дня более, чем на 10 лет, обычно не используются. Помимо существенного влияния дисконтирования, еще и точность оценки отдаленных по времени денежных потоков существенно ниже.
История с выбором между двумя проектами А и Б будет продолжена в следующих публикациях на тему методов оценки инвестиционных проектов. К сожалению, большинство статей в Интернете на эту тему написано сухо и коротко, и многие из публикаций содержат ошибки, что недопустимо.
Расчет NPV — пример в Excel
В нашем компьютерном веке стало гораздо проще делать любые расчеты. В программе Excel есть функция, с помощью которой расчет NPV можно сделать быстрее, чем по таблицам. И не нужно дисконтировать каждый поток вручную. Проще зайти в раздел Excel Формулы —> Финансовые и выбрать функцию ЧПС.
Пример расчета NPV для проекта А показан ниже:
Единственная сложность заключается в том, что эта функция дисконтирует все потоки, которые вы выберете. Если же первый поток, как в проектах А и Б рассмотренных выше, приходится на период времени ноль, то его не надо вводить в ячейку значения. Первоначальная инвестиция в сумме -10,000 нужно добавить к тому значению, которое рассчитает функцию ЧПС. В этом примере дисконтируются ячейки B3-B6 (обведено красным в таблице), по ставке 0,10 (зеленый квадратик), приведенная стоимость получается равной 10,788.2. Если вычесть из этой суммы инвестицию 10,000, то получится NPV, равная 788,2. При расчете вручную мы получили 788,4, разница 0,2 получилась в результате округлений.
Другая функция программы Excel, расположенная в том же разделе финансовых формул, ЧИСТНЗ тоже считает приведенную стоимость денежных потоков, но она может это делать для неравных промежутков времени между потоками. В ней есть дополнительная ячейка, куда можно ввести диапазон дат, соответствующих времени поступления денежных средств.
И будет вам счастье и приличный счёт в банке.
Финансовая грамотность необходима каждому человеку. Современная экономика — это сложный механизм перекачивания денег из одного кармана в другой. И нужно не только научиться зарабатывать деньги, но и вкладывать их.
Учиться быть инвесторами желательно еще до того, как у вас появятся деньги. Если в будущем вам повезет, и вы выиграете миллион долларов в лотерею, то вы должны быть готовы к этому. Если вам удастся заработать достаточные для инвестирования средства, то тем более захочется распорядиться ими так, чтобы приумножить.
Другие статьи на этом сайте из рубрики «Финансы»:
Вернуться на главную страницу
Изучая чистую приведённую стоимость обязательно следует уделять серьёзное внимание показателю — ставка дисконтирования. Часто её именуют иначе — альтернативной стоимостью вложений. Показатель, используемый в формуле расчёта, обозначает минимальную величину доходности, которую инвестор считает для себя приемлемой при рисках, сопоставимых с имеющимися у реализуемого проекта.
Инвестор может оперировать средствами, привлекаемыми из различных источников (собственных либо заёмных).
1. В первом случае устанавливаемая ставка дисконтирования, является личной оценкой допустимых рисков рассматриваемого инвестиционного проекта.
Её оценка может иметь несколько подходов. Самые простые, это:
- Выбор безрисковой ставки, корректируемой с учётом вероятности возникновения специфических рисков.
В качестве таковой обычно рассматриваются доходность по ценным бумагам государства, в котором реализуется проект, ставка доходности по корпоративным облигациям компаний отрасли.
- Необходимая и минимально достаточная (с точки зрения потенциального инвестора) рентабельность (показатель ROE).
При этом, лицо, принимающее решение об инвестировании, определяет ставку дисконтирования по одному из возможных вариантов:
- в проект вкладываются средства, имеющиеся на депозите в конкретном банке. Следовательно, альтернативная стоимость не должна быть меньше имеющейся банковской ставки;
- В проект инвестируются средства, выведенные из бизнеса и являющиеся временно свободными. В случае возникновения потребности в них, оперативное изъятие всей суммы из проекта невозможно. Потребуется кредит. Поэтому в качестве текущей стоимости средств выбирается рыночная кредитная ставка;
- Средняя доходность основного бизнеса составляет Y%. Соответственно от инвестиционного проекта требуется получать не меньше.
2. При работе с заёмными средствами ставка будет рассчитана как величина производная от стоимости привлекаемых из различных источников средств.
Как правило ставка, устанавливаемая инвестором, в подобных случаях превышает аналогичный показатель стоимости заёмных денежных средств.
При этом не просто учитывается изменение стоимости средств во времени, но и закладываются возможные риски, связанные с неопределённостью поступления денежных потоков и их объёмов.
Это является главной причиной, по которой ставкой дисконтирования считают средневзвешенную стоимость привлекаемого для последующего инвестирования капитала (WACC).
Именно этот показатель рассматривается в качестве требуемой нормы доходности на средства, вложенные в конкретный инвестиционный проект.
Чем выше ожидаемые риски, тем выше ставка.
Расчётные методы определения данного параметра менее наглядны, чем графические. Особенно когда требуется сравнить привлекательность двух или более проектов.
Например, сравнивая проекты «А» и «Б» (смотри график) можно сделать следующие выводы:
Применение анализа дисконтированных денежных потоков.
Большая часть работы финансовых аналитиков включает оценку операций, связанных с текущими и будущими денежными потоками. В разделе, посвященному временной стоимости денег (TVM) представлена финансовая математика, необходимая для решения этих проблем, и проиллюстрированы методы решения основных типов задач. Рассмотрим основные сферы применения анализа дисконтированных денежных потоков.
Финансовые аналитики, обучающиеся по программе CFA, должны овладеть многочисленными способами практического применения TVM (или анализа дисконтированных денежных потоков) в анализе капитала, ЦБ и обязательств с фиксированным доходом и анализе деривативов, поскольку они изучают каждую из этих тем по отдельности.
Далее мы рассмотрим наиболее важные области применения TVM: чистую приведенную стоимость (NPV) и внутреннюю норму доходности (IRR) — в качестве инструментов для оценки денежных потоков, оценки доходности инвестиционного портфеля и расчета доходности денежного рынка.
Важные сами по себе, эти области применения финансового анализа денежных потоков также вводят концепции, которые проявляются во многих других инвестиционных контекстах.
Сферы применения NPV и IRR.
Применяя анализ дисконтированных денежных потоков во всех сферах финансов, мы постоянно сталкиваемся с двумя понятиями: чистая приведенная стоимость и внутренняя норма доходности.
Сфера их применения охватывает все области финансов. Однако бюджетирование капиталовложений может служить показательной отправной точкой. Бюджетирование капиталовложений важно не только в корпоративных финансах, но и в анализе рынка ценных бумаг, потому что аналитики по ценным бумагам должны уметь оценивать, насколько хорошо менеджеры инвестируют активы своих компаний.
Есть три основных направления принятия финансовых решений в большинстве компаний.
- Бюджетирование капиталовложений (англ. ‘capital budgeting’) — это распределение средств на относительно долгосрочные проекты или инвестиции. С точки зрения бюджетирования капиталовложений, компания представляет собой портфель проектов и инвестиций.
- Структура капитала (англ. ‘capital structure’) — это выбор долгосрочного финансирования для инвестиций, которые компания хочет сделать.
- Управление оборотным капиталом (англ. ‘working capital management’) — это управление краткосрочными активами компании (такими как товарно-материальные запасы) и краткосрочными обязательствами (такими как кредиторская задолженность перед поставщиками).
Что такое чистая приведенная стоимость и правило чистой приведенной стоимости?
Чистая приведенная стоимость характеризует стоимость инвестиций, а правило чистой приведенной стоимости — это метод выбора среди альтернативных инвестиций.
Чистая приведенная стоимость инвестиций (NPV, от англ. ‘net present value’) — это приведенная (текущая) стоимость притока денежных средств за вычетом приведенной стоимости оттока денежных средств.
Слово «чистая» (англ. ‘net’) в этом термине означает вычитание приведенной стоимости оттоков (затрат) инвестиций из приведенной стоимости притоков (доходов) для получения чистого финансового результата.
Процедура вычисления NPV и применения правила NPV заключаются в следующем:
1. Определите все денежные потоки, связанные с инвестициями — все притоки и оттоки.
При оценке денежных потоков мы руководствуемся двумя принципами.
- Во-первых, мы включаем в расчет только дополнительные денежные потоки, возникающие в результате осуществления проекта. Мы не учитывает невозвратные затраты (англ. ‘sunk costs’), т.е. расходы, которые были совершены до начала проекта и которые нельзя возместить в течение проекта.
- Во-вторых, мы учитываем налоговые последствия, используя стоимость денежных потоков после уплаты налогов.
2. Определите соответствующую ставку дисконтирования или ставку альтернативной доходности r для инвестиционного проекта.
Для дисконтирования денежных потоков часто используется средневзвешенная стоимость капитала (WACC).
Этот показатель представляет собой средневзвешенное значение ставок доходности после налогообложения для обыкновенных акций, привилегированных акций и долгосрочных долговых обязательств компании, где весом является доля каждого источника финансирования в целевой структуре капитала компании.
3. Используя эту ставку дисконтирования, найдите текущую (приведенную) стоимость (PV) каждого денежного потока.
Приток имеет положительный знак (+) и увеличивает NPV. Отток имеет отрицательный знак (-) и уменьшает NPV.
4. Суммируйте все приведенные значения стоимости.
Сумма приведенной стоимости всех денежных потоков (притоков и оттоков) является чистой приведенной стоимостью инвестиций.
5. Примените правило чистой приведенной стоимости.
Правило NPV (англ. ‘net present value rule’) заключается в следующем:
- Если NPV инвестиции является положительным значением, инвестор должен ее осуществить.
- Если NPV отрицательна, инвестор не должен осуществлять эту инвестицию.
- Если у инвестора есть две возможные инвестиции, но он может выбрать только одну (т.е. взаимоисключающие проекты), инвестору следует выбрать инвестицию с более высокой положительной NPV.
В чем смысл правила NPV?
При расчете NPV инвестиционного предложения мы используем оценочную альтернативную стоимость капитала в качестве ставки дисконтирования.
Альтернативная стоимость капитала (англ. ‘opportunity cost of capital’) — это альтернативный доход, выраженный в виде процентной ставки, который инвесторы упускают при осуществлении инвестиций.
Когда NPV положительна, инвестиции увеличивают свою стоимость, потому что их доходность выше альтернативной стоимости капитала.
Таким образом, компания, осуществляющая инвестиции с положительной NPV, увеличивает благосостояние акционеров.
Индивидуальный инвестор, осуществляющий инвестиции с положительной NPV, увеличивает личное благосостояние. Инвестиции же с отрицательной NPV, наоборот, уменьшают его благосостояние.
При финансовых вычислениях с использованием правила NPV будет полезно обратиться к следующей формуле:
\( \mathbf { NPV = \sum_{t=0}^{N} {CF_t \over (1+r)^t} } \) (формула 1),
где:
- CFt = ожидаемый чистый денежный поток в момент времени t.
- N = прогнозируемая длительность инвестиций.
- r = ставка дисконтирования или альтернативная стоимость капитала.
Исходные данные должны быть представлены на сопоставимой временной основе: если денежные потоки являются годовыми, N — это срок жизни проекта в годах, а r — годовая ставка.
Например, предположим, что вы рассматриваете предложение, которое требует первоначальных затрат в размере $2 млн. (CF0 = -$2 млн.).
Вы ожидаете, что предлагаемые инвестиции обеспечат чистые положительные денежные потоки в размере:
CF1 = $0.50 млн. в конце 1-го года,
CF2 = $0.75 млн. в конце 2-го года и
CF3 = $1.35 млн. в конце 3-го года.
Используя 10% в качестве ставки дисконтирования вы рассчитаете NPV следующим образом:
NPV = -$2 + $0.50/(1.10) + $0.75/ (1.10)2 + $1.35/(1.10)3
= -$2 + $0.454545 + $0.619835 + $1.014275
= $0.088655 млн.
Поскольку NPV в размере $88,655 является положительной, вы принимаете данное инвестиционное предложение в соответствии с правилом NPV.
Рассмотрим пример, в котором программа исследований и разработок оценивается с использованием правила NPV.
Пример оценки капиталовложений в НИОКР с использованием правила NPV.
Как аналитик из RAD Corporation, вы оцениваете программу НИОКР (R&D, от англ. ‘research and development’) на текущий год.
Руководство объявило, что намерено инвестировать $1 млн. в исследования и разработки.
Прогнозируемые дополнительные чистые денежные потоки составляют $150,000 в год в течение неограниченного срока.
Альтернативная стоимость капитала RAD Corporation составляет 10%.
1. Определите, извлекут ли выгоду акционеры из программы НИОКР в соответствии с правилом NPV.
2. Оцените, изменится ли ваш ответ на 1-й пункт, если альтернативная стоимость капитала корпорации RAD составляет 15%, а не 10%.
Решение 1-й части:
Ежегодные положительные чистые денежные потоки в размере $150,000, которые мы можем обозначить как \(\overline{CF}\), образуют перпетуитет (т.е., бесконечную последовательность денежных потоков).
Приведенная стоимость (PV) перпетуитета равна \(\overline{CF} / r \), поэтому мы рассчитываем NPV проекта как:
\( NPV = CF_0 + \overline{CF}/r \)
= -$1,000,000 + 150,000/0.10 = $500,000
При ставке альтернативной стоимости капитала в 10% приведенная стоимость (PV) притока денежных средств по программе НИОКР составляет $1.5 млн.
Стоимость программы НИОКР — это немедленный единовременный отток в $1 млн. Следовательно, ее чистая приведенная стоимость (NPV) составляет $500,000.
Поскольку NPV положительна, вы делаете вывод, что программа исследований и разработок RAD Corporation принесет пользу акционерам.
Решение 2-й части:
При альтернативной стоимости капитала в 15% вы рассчитываете NPV так же, как вы делали выше, только на этот раз вы используете 15-процентную ставку дисконтирования:
NPV = -$1,000,000 + $150,000/0.15 = $0
При более высокой альтернативной стоимости капитала приведенная стоимость (PV) притоков меньше, а NPV программы меньше: она равна $0.
При NPV = 0 программа НИОКР генерирует достаточный денежный поток, чтобы компенсировать акционерам альтернативную стоимость инвестиций.
Когда компания берет проект с нулевой NPV, компания становится больше (т.е. это идет на пользу компании), но благосостояние акционеров не увеличивается.
что это такое и как рассчитать – SPRINTinvest.RU

Тема сегодняшней публикации для читателей нашего блога не нова. О том, что такое NPV и как рассчитать этот показатель, мы с той или иной степенью детализации уже вели речь в публикациях, посвященных теоретическим аспектам чистой приведенной стоимости.
Для более глубокого усвоения представленного ниже материала рекомендуем освежить в памяти некоторые концепции, бегло пробежавшись по следующим статьям:
- Приведенная стоимость: понятие и метод расчета
- На подступах к чистой приведенной стоимости
- Призрак «ЧПС», или как принимать обоснованные инвестиционные решения
- Приведенная стоимость сложных процентов
- Расчет чистой приведенной стоимости в Excel
- Главный критерий принятия инвестиционных решений
- Как оценить облигацию по формулам приведенной стоимости
- Расчет NPV в Excel (пример)
- Расчет NPV: онлайн-калькулятор
Представленного в этих статьях материала хватит вполне, чтобы почувствовать себя спецом в весьма тонких вопросах финансовой математики, без которых не обходится ни один профессиональный инвестор (в их числе, разумеется, и Уоррен Баффет).
Повторяться мы не станем. Наша задача – разобрать несколько практических примеров, которые помогут буквально почувствовать нутром смысл формулы NPV, включая каждый из входящих в нее параметров.
Что такое NPV
Традиционная расшифровка аббревиатуры NPV такова — Net Present Value.
Дословный перевод допускает троякое прочтение:
[1] чистый дисконтированный доход (сокращенно – ЧДД; это сокращение нередко включается в математические формулы русскоязычных учебников),
[2] чистая текущая стоимость (сокращение ЧТС практически хождения в научной литературе не имеет) и – самое распространенное —
[3] чистая приведенная стоимость (ЧПС).
Все три прочтения суть идентичны. С математической точки зрения, NPV – это величина, равная сумме приведенных к сегодняшнему дню дисконтированных денежных потоков.
Инвестиционный смысл этого определения в том, чтобы показать размер финансовой отдачи от вложений в инвестиционный проект с учетом сопутствующих инвестициям затрат.
С этих позиций NPV может служить мерилом прибыли инвестора.
Если эта величина положительна, значит инвестиция окупится, и инвестор получит прибыль.
Если NPV окажется отрицательной величиной, это свидетельство убыточности проекта.
Теоретически NPV может оказаться равным нулю, что будет означать лишь то, что начальные вложения в проект окупятся, но не более того. Лучше поискать проект с большей финансовой отдачей.
Традиционно расчет NPV служил (и служит до сих пор) действенным критерием принятия решений о вложении либо отказе от вложения денежных средств в тот или иной проект.
С 2012 г. с подачи Организации Объединенных Наций по промышленному развитию (ЮНИДО) общепризнанным подходом к выбору наилучшего инвестиционного решения считается расчет индекса скорости удельного прироста стоимости, включающего в себя и расчет NPV.
Последний метод предложен в 2009 г. группой экономистов во главе с российским ученым А.Б. Коганом и весьма эффективен при сравнении альтернатив с разными параметрами (то есть в ситуациях, где традиционные методы NPV и IRR либо противоречат друг другу, либо приводят к неоднозначным выводам).
Указанному методу мы в ближайшем будущем посвятим отдельную публикацию.
Сейчас же сосредоточимся на том, как рассчитать NPV проекта, используя для этих целей известную формулу.
NPV: формула расчета (пример)
Задача. Имеется три потенциальных проекта для инвестиций. Первоначальные инвестиции С0 в каждый из них составляют 400 условных единиц. Известна прибыль (Пn) , которую смогут генерировать проекты в ближайшие пять лет:
| Проект | Начальные инвестиции | Прибыль по годам | ||||
| П1 | П2 | П3 | П4 | П5 | ||
| Проект 1 | 400 | 80 | 105 | 120 | 135 | 150 |
| Проект 2 | 400 | 100 | 117 | 124 | 131 | 118 |
| Проект 3 | 400 | 100 | 125 | 90 | 130 | 145 |
Норма прибыли i составляет 13 %. Необходимо выбрать наиболее выгодный проект, используя формулу NPV.
Решение. Интересующая нас формула имеет следующий вид:

В этой формуле CFt обозначает чистый эффективный денежный поток на t-ом годичном интервале, i — ставка дисконтирования (в десятичном выражении), N – количество лет.
В представленной формуле главное разглядеть фактор (коэффициент) дисконтирования 1/(1 + i)t.
В нашем случае для t = 0 он будет равен 1, для t = 1: 1/(1+0,13)1 = 0,885 и т.д.
Рассчитаем значения NPV для каждого из трех проектов, используя табличное представление (оно более наглядно).
| Проект 1 | |||
| Год | Денежный поток | Коэффициент дисконтирования | Дисконтированный денежный поток |
| 0 | -400 | 1,000 | -400 |
| 1 | 80 | 0,885 | 70,80 |
| 2 | 105 | 0,783 | 82,22 |
| 3 | 120 | 0,693 | 83,16 |
| 4 | 135 | 0,613 | 82,76 |
| 5 | 150 | 0,543 | 81,45 |
| NPV = | 0,39 | ||
| Проект 2 | |||
| Год | Денежный поток | Коэффициент дисконтирования | Дисконтированный денежный поток |
| 0 | -400 | 1,000 | -400 |
| 1 | 100 | 0,885 | 88,50 |
| 2 | 117 | 0,783 | 91,61 |
| 3 | 124 | 0,693 | 85,93 |
| 4 | 131 | 0,613 | 80,30 |
| 5 | 118 | 0,543 | 64,07 |
| NPV = | 10,41 | ||
| Проект 3 | |||
| Год | Денежный поток | Коэффициент дисконтирования | Дисконтированный денежный поток |
| 0 | -400 | 1,000 | -400 |
| 1 | 100 | 0,885 | 88,50 |
| 2 | 125 | 0,783 | 97,88 |
| 3 | 90 | 0,693 | 62,37 |
| 4 | 130 | 0,613 | 79,69 |
| 5 | 145 | 0,543 | 78,74 |
| NPV = | 7,18 | ||
Наибольший NPV имеет проект 2. С точки зрения NPV, этот проект и является самым выгодным.
Разумеется, вместо таблиц мы бы могли использовать иное представление решения:
NPV1 = -400 * 1,000 + 80 * 0,885 + 105 * 0,783 + 120 * 0,693 + 135 * 0,613 + 150 * 0,543 = 0,39
NPV2 = -400 * 1,000 + 100 * 0,885 + 117 * 0,783 + 124 * 0,693 + 131 * 0,613 + 118 * 0,543 = 10,41
NPV3 = -400 * 1,000 + 100 * 0,885 + 125 * 0,783 + 90 * 0,693 + 130 * 0,613 + 145 * 0,543 = 7,18
Результат расчета NPV будет тот же.
На этом простом примере мы показали, как считать NPV, когда заранее известен объем первоначальных инвестиций и ожидаемые размеры прибыли на ближайшую перспективу.
На практике эти значения известны далеко не всегда, что существенно усложняет задачу выбора наиболее выгодного инвестиционного проекта.
Применение одного лишь метода NPV в таких ситуация может привести к неверным выводам: либо прибыль окажется невысока, либо ждать ее придется неоправданно долго.
Компенсировать недостатки NPV призваны другие расчетные показатели (уже упомянутый нами IRR, отражающий внутреннюю норму доходности, и некоторые другие).
Думается, после проработки сегодняшней статьи вы уже не будете задаваться вопросом при виде загадочной трехбуквицы NPV, что это такое и как рассчитать сей показатель.
Удачных инвестиций!
NPV инвестиционного проекта: формула | Vse-Investicii

 Инвестирование — это вложение свободных финресурсов с намерением приобретения стабильной выгоды в перспективе. Вложиться можно в так называемые «квазиденьги» (ценные бумаги, денежные обязательства, фьючерсы, опционы и т. д.), в новый проект, в развитие начатого бизнеса. Чтобы избежать ошибок в расчётах, можно применить НПВ или NPV инвестиционного проекта — один из приёмов мониторинга результативности бизнес-проектов.
Инвестирование — это вложение свободных финресурсов с намерением приобретения стабильной выгоды в перспективе. Вложиться можно в так называемые «квазиденьги» (ценные бумаги, денежные обязательства, фьючерсы, опционы и т. д.), в новый проект, в развитие начатого бизнеса. Чтобы избежать ошибок в расчётах, можно применить НПВ или NPV инвестиционного проекта — один из приёмов мониторинга результативности бизнес-проектов.
Варианты вложений
Существует три способа распоряжения денежными средствами проекта: расходование, сбережение, инвестиционный. Самым простым, но не самым доходным вариантом является вложение средств в банк, покупку долговых обязательств или банковских акций, свободно обращающихся на финансовой бирже.
Однако лучшим инвестиционным шагом будет вложение в расширение собственного бизнеса. Это подразумевает покупку долгосрочных финактивов (ОС или основных средств), использование которых в торговых или производственных процессах сформирует стабильные финансовые поступления.
Для определения успешности определённого инвестиционного проекта, бизнес-экспертами применяются конкретные методики анализа бизнес-планов. В оценке используются два ключевых механизма:
- IRR, иначе InternalRate of Return в переводе с английского — внутренняя норма доходности;
- NPV или Net PresentValue — чистая приведённая стоимость.
NPV проекта представляет коэффициент прибыли, получаемой участниками инвестиционных бизнеспроектов. С точки зрения математики NPV, это параметр рассчитывается через дисконтированные показатели чистых финансовых потоков, несмотря на значения как «+», так и «-». NPV можно определить за любой временной промежуток исчисляя с момента открытия проекта.
Функциональное назначение NVP
Чистый приведённый доход NPV нужен, чтобы иметь представление о доходности либо убыточности инвестиционного бизнес-проекта, об объёме финсредств за определённый отрезок времени, а также для сравнения инвестпроектов и определения их окупаемости.
Проще говоря, способ вычисления чистой текущей инвестиционной стоимости (ЧТС) выражается в разнице между денежным притоком и оттоком, предоставленным на текущий момент. Он отображает объём общего прироста, полученного вкладчиком от инвестиционного бизнес проекта, принимая во внимание временную стоимость и все финансовые риски.
NPV даёт возможность инвесторам принять решение по следующим вопросам:
- есть ли смысл связывать инвестиционные цели с предложенным проектом;
- на каком из предложенных вариантов остановить свой выбор;
- какими будут значения внутренней IRR.
В некоторых случаях NPV характеризуется как добавленная стоимость инвестиционного бизнес проекта. Вместе с тем инвестиции обоснованы лишь в тех случаях, если они в полном объёме возмещают стартовые капиталовложения, перекрывают уровень инфляции и предоставляют возможность инвестору получить прибыль.
Способы расчета ЧПС
При помощи чистого дисконт дохода проекта можно дать оценку инвестиционному КПД. Формула подсчёта чистой текущей стоимости бизнеса выглядит следующим образом:
 , где:
, где:
- N — число временных промежутков, за которые необходимо рассчитать инвестпроект;
- t — время, за которое принимается чистый финпоток;
- CF — ∑ чистых финпоступлений;
- Программа Excel даёт возможность посчитать чистую текущую инвестиционную стоимость несколькими способами. Формула расчёта NPV будет работать только при корректно заданной ставке дисконта и выделенном «коридоре» NPV или ЧДП. Для начала работы в Excel выбирается вкладка «формула», после этого «финансовые» в заключении «ЧПС».В ячейке «аргументы функции» выбирают строку «Ставка» и указывают величину дисконтставки. В строчке «Значение 1» вписывают приведённые финансовые потоки NPV. Важно! В отмеченном диапазоне нужно отключить первую ячейку со стартовыми вложениями. Иначе чистый инвестиционный дисконтдоход проекта будет показывать неточный результат.
С использованием калькулятора
Дисконтная ставка проекта для NPV может быть рассчитана несколькими способами. К примеру, взять её эквивалентной рентабельности по минимальной инвестиционной доходности консервативных вложений средств. Или же принять в виде дисконта для NPV процентную ставку кредита либо индекс процентного преобразования величины цен за конкретный временной отрезок. «Ручной» мониторинг осуществляется поэтапно:

- Считается сумма первоначальных капиталовложений (к ним относятся все денежные средства, которые инвестор планирует вложить на начальной стадии, в том числе непрямые затраты).
- Выбирается временной отрезок (t) для инвестиционного анализирования.
- Определяется финансовый поток проекта за все временные отрезки. Если необходимо найти чистый дисконтированный доход на 6 лет, то и инвестиционных финансовых потоков будет также 6. Между ними может быть разница по объёму, но они могут быть и одинаковыми.
- Устанавливается дисконт ставка.
- Уменьшаются финпотоки за каждый год на дисконтставку (дисконтирование финпоступлений).
- Выполняется суммирование всех полученных инвестиционных дисконтпотоков. Из результата вычитается ∑ стартовых капиталовложений.
Произвести математический расчёт чистой текущей стоимости проекта довольно просто. Достаточно знать все переменные величины для определения чистого дисконтированного дохода. Но именно на этом этапе у большинства инвесторов возникают трудности.
Информативность табличной формы проигрывает графической, поэтому более содержательный инвестиционный результат будет виден на графике.
Определение ставки дисконтирования R
% ставку, задействованную в переоценке предполагаемых инвестиционных поступлений в общий показатель текущей стоимости, называют дисконтставкой. Обычно это % отчисление, под которое инвестор имеет возможность привлекать денежные финсредства в проект.
Существует несколько способов привлечения инвестиционных финресурсов:
- оформление банковского кредита;
- получение инвестиционного займа на выгодных условиях;
- внесение личных накоплений, полученных от продажи имущества или вывода капитала из других проектов.
Стоимость средств компании будет отличаться в любом из перечисленных вариантов. Даже кредитные ставки существенно различаются исходя из платёжеспособности компании, продолжительности, суммарного объёма инвестиционных средств и наличия залога.
Ставка дисконта определяется инвесторами путём расчёта средневзвешенной величины. Этот метод вычисления инвестиционного дисконта по капиталовложениям носит название WACC (Weight Average Cost of Capital).
Денежные потоки (CF)
На этом этапе необходимо знать предварительно ∑ всех притоков по инвестпроекту и расходы на него. Когда рассматривается процесс компании инвестора, то необходимо будет вычислять объем и ∑ предполагаемых продаж, а параллельно с этим, произвести достоверную калькуляцию всего бюджета проекта (арендная плата, сырьевые материалы, налоговые сборы, выплата заработной платы, логистика и пр.).
Анализируя потенциальные поступления, необходимо дать определение характеру и степени обусловленности между воздействием причин, формирующих инвестиционные финансовые потоки и самим заполнением денежных зачислений.
При положительном значении NPV инвестиционный проект станет прибыльным. Отрицательное значение NPV свидетельствует об убыточности проекта. Лучшим решением будет воздержаться от него или откорректировать первичные данные. Если величина NPV равна нулю, проект окупится, но получить прибыль не получится.
Положительные и отрицательные стороны метода NPV
Достоинство метода с NPV выражается в чёткости показателей для координационных решений на момент выбора объекта вложения. Это предоставляет возможность инвестору иметь представление о ситуации при принятии взвешенного решения.
Метод NPV имеет ряд недостатков:
- не учитывается выполнимость реинвестирования приобретаемых доходов;
- в NPV не рассматриваются расхождения в периодах реализации инвестпроектов;
- сложность выбора временного отрезка благоприятного для проекта;
- величина финансовых потоков, представляющая собой прогнозное значение, не рассматривает в NPV исход событий.
Каждый инвестиционный проект квалифицируется одновременно по ряду характеристик. Помимо (NPV), вкладчики нередко берут во внимание PI — коэффициент экономической эффективности, индекс по внутренней норме доходности (IRR) и дисконтированную продолжительность окупаемости вложений (DPP).
А вы рассчитываете NPV инвестиционного проекта, планируя вклад?
 Загрузка…
Загрузка…NPV — метод чистой текущей стоимости
Область применения
NPV показывает чистые доходы или чистые убытки инвестора при помещении денег в проект по сравнению с хранением их в банке.
Описание
Величина NPV (Net Present Value) отражает чистую текущую стоимость и рассчитывается как разность между инвестициями и будущими доходами, выраженная в денежной величине, приведенной к началу реализации проекта, т. е. с учетом ставки дисконтирования.
Для определения NPV необходимо рассчитать текущую стоимость будущих оттоков и притоков денежных средств. При заданной норме дисконта её можно определить на протяжении всего жизненного цикла проекта, а также сопоставить приведенные суммы друг с другом.
Метод дисконтирования денежных поступлений – исследование денежного потока наоборот, т. е. от будущего к текущему моменту времени, позволяет привести будущие денежные поступления к сегодняшним условиям. Для этого используют формулу:
${PV_n}=\frac{CF_n}{(1+r)^n}={CF_n}*k_d$,
где $k_d$ — коэффициент дисконтирования,
$CF_n$ — доход от проекта за конкретный год,
$n$ — срок проекта в годах.
При начислении процентов несколько раз в году по сложной ставке применяется такая формула:
$${PV_n}=\frac{CF_n}{(1+\frac{r}{m})^{nm}}$$
Результатом сопоставления полученной величины и первоначальных инвестиций будет чистая текущая стоимость, которая показывает экономический результат реализации проекта.
$NPV=PV-CI$,
где $CI$ — сумма первоначальных инвестиций.
Если капитальные вложения, связанные с реализацией проекта, осуществляются в несколько этапов, то расчет показателя $NPV$ производится по следующей формуле:
$NPV = \sum \limits_{i=0}^{n} \frac{CF_i}{(1+r)^i} — \sum \limits_{i=0}^{n}\frac{CI_i}{(1+r)^i}$.
Интерпретация результатов:
- $NPV>0$ — проект является прибыльным и по окончании будет обеспечено получение прибыли согласно заданной ставке дисконта, а также будет получен дополнительный доход, равный величине $NPV$;
- $NPV=0$ — проект лишь окупает первоначальные затраты;
- $NPV
Важно: NPV показывает величину прибыли от инвестиции, и стоит предположить, что чем больше инвестиция, тем больше чистая текущая стоимость. Поэтому сравнение нескольких инвестиций разного размера с помощью этого показателя невозможно. Кроме того, величина NPV не несёт информации о периоде, через который инвестиция окупится.
При анализе проектов с различными исходными характеристиками (суммами первоначальных инвестиций, сроками экономической жизни и т. д.), кроме $NPV$, рассчитывают относительные показатели: индекс рентабельности и внутреннюю норму дохода.
Алгоритм
- Рассчитываем коэффициент дисконтирования ${k_d}=\frac{1}{(1+r)^n}$.
- Рассчитываем дисконтированные денежные поступлений $PV$.
- Рассчитываем дисконтированные денежные инвестиций $CI$.
- Рассчитать чистую текущую стоимость доходов $NPV$.
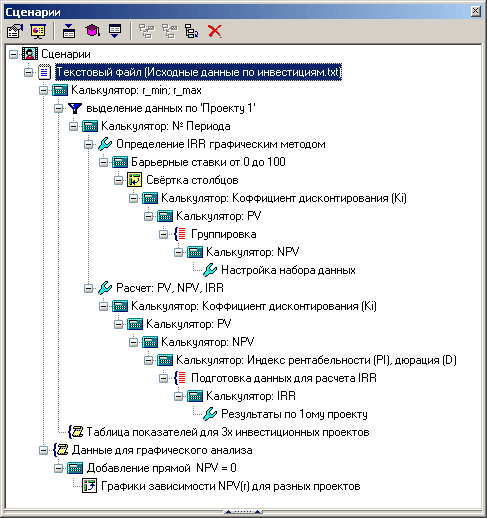
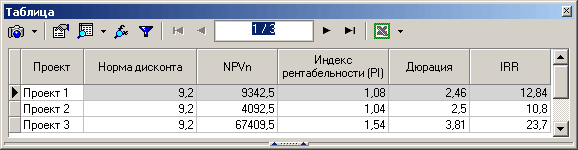
Требования к данным
| Имя поля | Метка поля | Тип данных | Вид данных |
|---|---|---|---|
| Year | Год | Целый | Непрерывный |
| Cash_flow | Денежные поступления | Вещественный | Непрерывный |
| Rate | Норма дисконта | Вещественный | Непрерывный |
| Investment | Инвестиции | Вещественный | Непрерывный |
| Project | Проект | Строковый | Дискретный |
Сценарий
Чистая приведённая стоимость (NPV) | КАЛЬКУЛЯТОР
Чистая приведённая стоимость (ЧПС, чистая текущая стоимость, чистый дисконтированный доход, ЧДД, англ. Net present value, принятое в международной практике для анализа инвестиционных проектов сокращение — NPV) — это сумма дисконтированных значений потока платежей, приведённых к сегодняшнему дню.
Метод чистой приведенной стоимости получил широкое применение при бюджетировании капитальных вложений и принятии инвестиционных решений. Также NPV считается лучшим критерием отбора для принятия или отклонения решения о реализации инвестиционного проекта, поскольку основывается на концепции стоимости денег во времени. Другими словами, чистая приведенная стоимость отражает ожидаемое изменение благосостояния инвестора в результате реализации проекта.
Формула NPV
Чистая приведенная стоимость проекта является суммой настоящей стоимости всех денежных потоков (как входящих, так и исходящих). Формула расчета выглядит следующим образом:


Где:
- CFt – ожидаемый чистый денежный поток (разница между входящим и исходящим денежным потоком) за период t,
- r – ставка дисконтирования,
- N – срок реализации проекта.
Ставка дисконтирования
Важно понимать, что при выборе ставки дисконтирования должна быть учтена не только концепция стоимости денег во времени, но и риск неопределенности ожидаемых денежных потоков! По этой причине в качестве ставки дисконтирования рекомендуется использовать средневзвешенную стоимость капитала (англ. Weighted Average Cost of Capital, WACC), привлеченного для реализации проекта. Другими словами, WACC является требуемой нормой доходности на капитал, инвестированный в проект. Следовательно, чем выше риск неопределенности денежных потоков, тем выше ставка дисконтирования, и наоборот.
Критерий отбора проектов
Правило принятия решения об отборе проектов при помощи NPV метода довольно прямолинейно. Нулевое пороговое значение говорит о том, что денежные потоки проекта позволяют покрыть стоимость привлеченного капитала. Таким образом, критерии отбора можно сформулировать следующим образом:
- Отдельно взятый независимый проект должен быть принят при положительном значении чистой приведенной стоимости или отклонен при отрицательном. Нулевое значение является точкой безразличия для инвестора.
- Если инвестор рассматривает несколько независимых проектов, принять следует те из них, у которых наблюдается положительный NPV.
- Если рассматривается ряд взаимоисключающих проектов, выбрать следует тот из них, у которого будет максимальная чистая приведенная стоимость.
Об авторе