Сзв м бланк: Новая форма СЗВ-М

Сзв м бланк: Новая форма СЗВ-М

Новая форма отчета СЗВ-М в 2017 году

Утверждена ли новая форма отчета СЗВ-М с 2017 года? Где можно скачать бланк новой формы СЗВ-М, подлежащей сдаче в ПФР? Готов ли образец заполнения новой формы СЗВ-М для ПФР? По какой форме сдавать СЗВ-М за январь 2017 года? Ответы на эти и другие вопросы вы найдете в данной статье. Также рекомендуем ознакомиться со статьей «Страховые взносы с 2017 года: обзор изменений».

Новая форма СЗВ-М с 2017 года: утверждена или нет

В 2017 года страхователям (организация и ИП) отчет по форме СЗВ-М нужно будет сдавать в территориальные подразделения ПФР. Сроки сдачи отчетов СЗВ-М изменились. См. «СЗВ-М в 2017 году: новые сроки сдачи исходных, корректирующих и уточненных отчетов».

Форма отчета СЗВ-М – это сведения индивидуального (персонифицированного) учета. В 2017 году за ПФР сохранилось право на утверждение новой формы и формата отчетов СЗВ-М. Об этом сказано пункте 2 статьи 8 Федерального закона от 01.04.1996 № 27-ФЗ «Об индивидуальном (персонифицированном) учете в системе обязательного пенсионного страхования».

Таким образом, ПФР мог бы воспользоваться данным правом и утвердить новую форму СЗВ-М, применяемую с 2017 года.
Теперь посмотрим на официальный сайт ПФР в раздел «Проекты нормативно-правовых актов ПФР». В этом разделе ПФР публикует документы, которые необходимо утвердить. Однако в этом разделе нет никакой информации о том, что новая форма отчета СЗВ-М планируется к применению с 2017 года. Соответственно, можно сказать, что новой формы СЗВ-М с 2017 года не будет. Новый бланк и не планировалось утверждать.

Новый отчет с 2017 года: нужен ли?

Стоит заметить, что все страховые взносы (кроме взносов «на травматизм») с 2017 года переходят под контроль ФНС. Однако ПФР продолжит полностью контролировать индивидуальный персонифицированный учет и принимать соответствующую отчетность. См. «Органы контроля за уплатой страховых взносов с 2017 года».

При этом в законодательстве о персонифицированном учете с 2017 года не произошло никаких изменений, которые бы требовали утверждения новой формы СЗВ-М с 2017 года.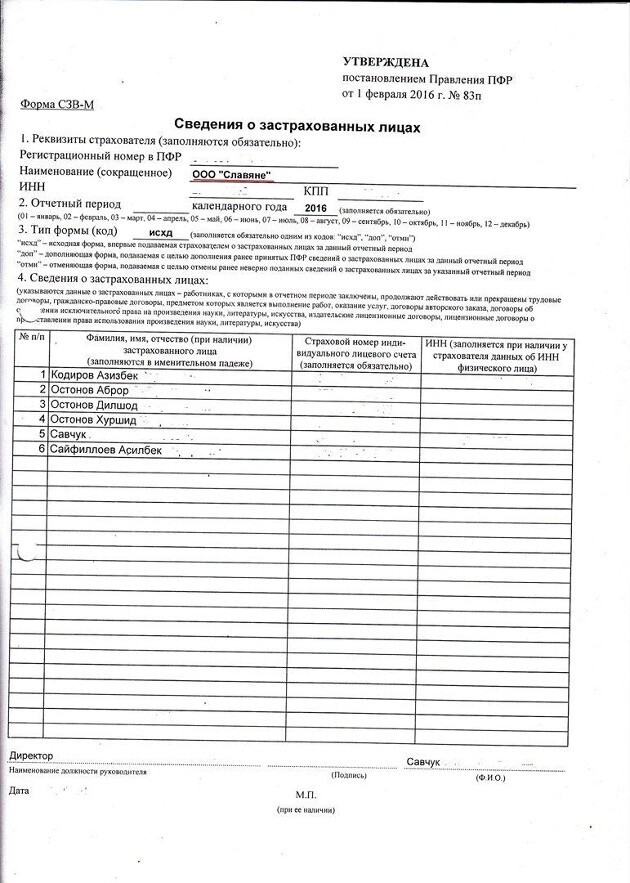

В 2017 году, как и прежде, в отчете нужно показывать (п.2.2 ст. 11 Федерального закона от 01.04.1996 № 27-ФЗ ):

• СНИЛС;
• Ф.И.О.;
• ИНН (при наличии у страхователя данных об ИНН застрахованного лица).

Действующая форма СЗВ-М «Сведения о застрахованных лицах», утвержденная Постановлением Правления ПФР от 01.02.2016 № 83п, позволяет отражать в ней указанную информацию. Соответственно, утверждать новый бланк СЗВ-М с 2017 года и не потребовалось.

Где скачать новый бланк СЗВ-М

Новый бланк формы СЗВ-М с 2017 года скачивать не потребуется тем, кто сдает ежемесячные отчеты ПФР в электронном виде. Ведь формы персонифицированной отчетности, уже включены в состав бухгалтерских программ, которые применяются для заполнения отчетности.

Если же организация отчитывается «на бумаге», то бланк для заполнения СЗВ-М в 2017 году вы можете скачать на нашем сайте в удобном Excel формате. См. «Форма «сведения о застрахованных лицах» (СЗВ-М)». Однако стоит сказать, что многих бухгалтеров данная форма должны была сохраниться с 2016 года.

Скачать бланк СЗВ-М с 2017 года в формате Excel.

Заметим, что в 2017 году если в СЗВ-М за месяц включено 25 или более «физиков», то страхователь (организация ил ИП) обязан передать отчетность через Интернет в качестве электронного документа, подписанного усиленной квалифицированной электронной подписью. Если же в отчете меньше 25 человек, то допускается представление «бумажного» отчета (абз. 3 п. 2 ст. 8 Федерального закона от 01.04.1996 № 27-ФЗ).

Новый формат СЗВ-М с 2017 года

Формат отчета СЗВ-М нужен в целях сдачи отчетности в территориальные органы ПФР в электронном виде. Он утвержден распоряжением от 31.08.2016 № 432р. См. «ПФР утвердил новый формат отчета СЗВ-М».

При этом, учитывая, что новая форма отчета СЗВ-М на 2017 год утверждена не была, то и новый формат отчета разрабатывать и утверждать Пенсионному фонду не потребовалось. То есть, в 2017 году применяется прежний формат.

Новая форма СЗВ-М 2017 года: образец

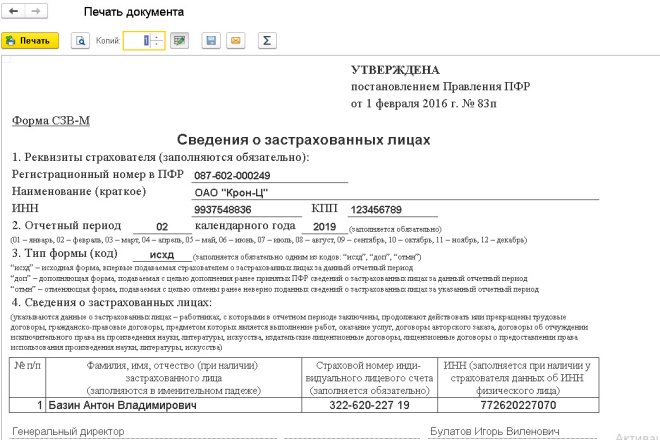
Далее приведем образец заполнения формы СЗВ-М в 2017 году. Как мы уже сказали, что нового бланка на 2017 год не утверждалось. Поэтому приведем образец заполнения формы, которая продолжила действовать в 2017 году. Так, например, образец заполнения СЗВ-М за январь 2017 года будет выглядеть так:

Скачать пример заполнения формы СЗВ-М с 2017 года.машина опорных векторов

— формулировка и вывод | by Atul Agarwal

Photo by Andy Holmes on Unsplash

Предсказание качественных ответов в машинном обучении называется классификацией .

SVM или метод опорных векторов — это классификатор, максимизирующий маржу. Цель классификатора в нашем примере ниже — найти прямую или (n-1) размерную гиперплоскость, которая разделяет два класса, присутствующих в n-мерном пространстве.

В нашем примере, приведенном ниже, мы видим, что любой алгоритм обучения выдаст любую из указанных строк, но какая строка может быть лучшей?

2-мерное представление двоичных классов

Интуитивно зеленая линия кажется лучшим решением, поскольку она, вероятно, даст лучший прогноз для будущего набора тестовых данных. Мы формализуем концепцию качества классификатора, введя параметр, называемый границей, шириной полосы вокруг границы решения/классификатора без каких-либо обучающих выборок.

Следовательно, цель состоит в том, чтобы найти границу решения с максимальным запасом. Мы можем рассматривать границу как область вокруг тренировочной области, вокруг которой не может проходить граница решения. По мере увеличения радиуса допустимая область уменьшается, она сходится к одной прямой.

Примечание. Есть только несколько обучающих выборок с пузырьками, которые касаются границы решения. Эти выборки по существу называются опорными векторами.

В 1970 году математики Вапник и Червоненкис ввели понятие размерности ВК, где они оценили будущую ошибку тестирования (R(α)) как функцию ошибки обучения и некоторую функцию размерности ВК (монотонно возрастающую функцию).

Размер VC, h, был записан как минимум, обратный квадрату относительного поля и размерам данных. Следовательно, если бы мы могли максимизировать относительную маржу, мы бы минимизировали ее обратный квадрат, и если она упадет ниже размерности данных, h станет независимым от размерности.

Примечание: относительный запас — это не что иное, как запас, деленный на диаметр круга, охватывающего все тренировочные точки.

Используем подход 2 и формулируем задачу так:

Интегрируя константы в лагранжевой форме, получаем:

Метод множителей Лагранжа утверждает, что J минимизируется для w и b, как и прежде, но должно быть максимизировано для α. Точка, которую представляет J, называется седловой точкой.

Функция J в настоящее время представлена ​​в своей первичной форме, мы можем преобразовать ее в двойственную форму для решения.

Кроме того, из условия KKT множителей Лагранжа мы можем сказать, что все члены, соответствующие множителям Лагранжа в функции J, должны стремиться к 0 в оптимуме.

Это означает, что ненулевые коэффициенты Лагранжа соответствуют точкам данных опорного вектора. Используя приведенные выше уравнения, мы можем записать J как:

Q(α) представляет собой двойственную форму J, которая зависит только от α, поскольку все остальные являются известными скалярами. Мы можем найти Q(α) с любой оптимизацией QP, что выходит за рамки этой статьи. Получив α, мы получаем w, и, следовательно, любой из этих опорных векторов даст b из условия KKT.

Мы рассмотрели случай, когда данные линейно разделимы. Теперь мы рассмотрим случаи, когда данные могут быть неразделимы линейно из-за

Зашумленных данных

Для зашумленных данных мы вводим параметр ошибки обучения в нашу оценку/оптимизацию. Мы вводим резервную переменную и добавляем дополнительное условие как

Повторяя тот же процесс снова с коэффициентами Лагранжа, мы получаем

Единственное отличие состоит в том, что теперь есть ограничение на коэффициенты Лагранжа. Параметр C контролирует относительный вес между ошибкой обучения и размерностью VC.

Любой набор данных с нелинейной границей теоретически будет линейно разделимым при проецировании на более высокие измерения.

Следовательно, Q(α) можно записать как:

Мы можем написать w и другие уравнения фазы тестирования, например:

Мы можем видеть, что отображение происходит как точечный продукт как при обучении, так и при тестировании. Поскольку мы не знаем отображения, мы можем найти функцию K(x,y) , которая эквивалентна скалярному произведению отображения; мы можем избежать явного отображения на более высокое измерение.

Давайте возьмем пример квадратичного ядра, чтобы лучше понять.

Мы видим меньшую вычислительную сложность с функциями ядра по сравнению с отображением и последующим умножением.
Это может быть расширено до n-мерного ядра. Следовательно, n-мерное отображение/ядро может быть представлено как

Примечание. Добавление двух действительных ядер также дает нам ядро. Это можно легко доказать.

Следовательно, чтобы отобразить в чрезвычайно высокое измерение, мы можем вычислить ядро ​​как:

Теоретически набор данных был бы линейно разделим, если бы отображался на гиперплоскость бесконечного измерения. Следовательно, если мы сможем найти ядро, которое давало бы произведение бесконечного отображения гиперплоскостей, наша работа выполнена.

Вот теорема Мерсера, она утверждает, что тогда и только тогда, когда K(X, Y) является симметричным, непрерывным и положительно полуопределенным (тогда условие Мерсера), оно может быть представлено как

Значение существования линейной комбинации отображения более высокой размерности гарантировано. Следовательно, теперь нам нужно только проверить, удовлетворяет ли функция условию Мерсера, и мы получаем отображение в бесконечной размерности.

На этом я заканчиваю свой блог об SVM, одном из лучших классификаторов, которые я использовал, смотрите это место для получения дополнительной информации.

Математика SVM | Math Behind Support Vector Machine

Эта статья была опубликована в рамках блога по науке о данных.

Введение

Один из классификаторов, с которым мы сталкиваемся при изучении машинного обучения, — это машина опорных векторов или SVM. Этот алгоритм является одним из самых популярных алгоритмов классификации, используемых в машинном обучении.

В этой статье мы узнаем о математике, лежащей в основе машины опорных векторов для задачи классификации, о том, как она классифицирует классы и дает прогноз.

 

Содержание

1. Нежное введение в метод опорных векторов (SVM)
2. Несколько понятий, которые нужно знать, прежде чем узнать секрет алгоритма
3. Погружение глубоко в море математики
   • 3.1 Где использовать SVM / Предыстория SVM
     • 3.1.1 Случай 1: Совершенно разделенный двоичный классифицированный набор данных
     • 3.1.2 Уравнение идеального разделения
   • 3. 2 Случай 2: набор данных несовершенного разделения
     • 3.2.1 Окончательное уравнение для решения несовершенного разделения
     • 3.2.2 Первичный – Двойственный – Лагранжев
     • 3.2.3 Использование ядра для получения окончательных результатов
4. Конечные точки

1. Машина опорных векторов

A Метод опорных векторов или SVM — это алгоритм машинного обучения, который просматривает данные и сортирует их по одной из двух категорий.

Машина опорных векторов — это линейный алгоритм машинного обучения с учителем, который чаще всего используется для решения задач классификации и также называется классификацией опорных векторов.

Существует также подмножество SVM, называемое SVR, что означает регрессию опорных векторов, в которой используются те же принципы для решения задач регрессии.

SVM наиболее часто используется и эффективен из-за использования метода ядра, который в основном помогает решить нелинейность уравнения очень простым способом.

 

П.С. — Так как эта статья написана с упором на математическую часть. Пожалуйста, обратитесь к этой статье для полного обзора работы алгоритма

.

2. Основные темы для SVM

Машина опорных векторов в основном помогает сортировать данные по двум или более категориям с помощью границы для различения похожих категорий.

Итак, сначала давайте пересмотрим формулы того, как данные представлены в пространстве, и что такое уравнение линии, которое поможет разделить похожие категории, и, наконец, формулу расстояния между точкой данных и линией (границей, разделяющей категории).

2.1 Точка в пространстве

Предположим, у нас есть некоторые данные, в которых нас (алгоритм SVM) просят различать мужчин и женщин, сначала изучив характеристики обоих полов, а затем точно пометив невидимые данные, если кто-то мужчина или женщина.

В этом примере характеристики, которые помогут различать пол, в основном называются признаками в машинном обучении.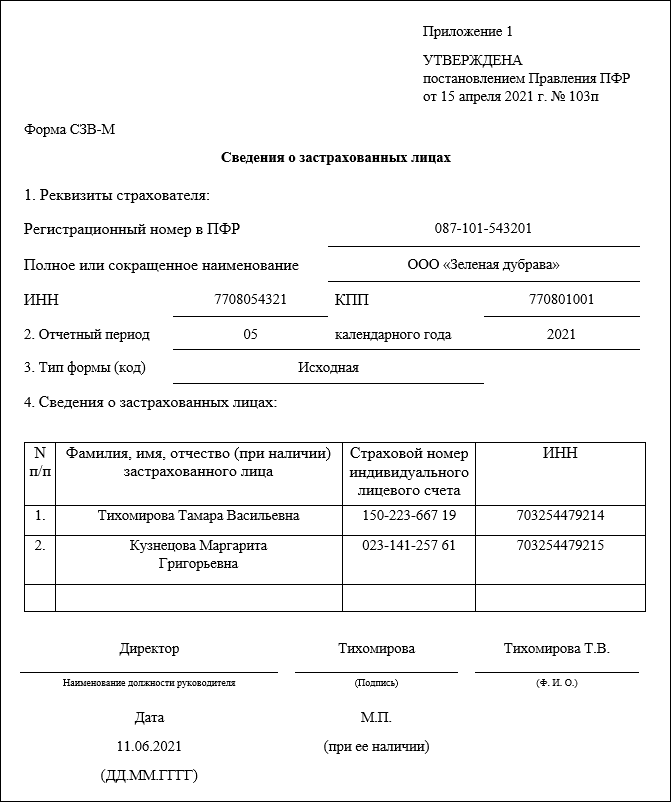

Домен

, совместный домен, диапазон

 

 

Предполагая, что мы уже знакомы с понятием домена, диапазона и совместного домена при определении функции в реальном пространстве. (Если нет, пожалуйста, нажмите на изображение для понимания концепции с примером)

Когда мы определяем x в реальном пространстве, мы понимаем его домен, а при отображении функции для y = f(x) мы получаем диапазон и со-область. 9D здесь — векторное пространство с размерностью D, для этого алгоритма не обязательно иметь представление об этом понятии.

Мы применяем аналогичную концепцию домена, диапазона, отображения функции для точек данных здесь, вместо реального пространства у нас есть векторное пространство для x.

Далее, отображая точку на сложном пространстве признаков x,

Φ(x) ∊ R ^M

Преобразованное пространство признаков для каждого входного признака, сопоставленного с преобразованным базисным вектором Φ(x), можно определить как :

2. 2 Граница принятия решения

Итак, теперь, когда мы представили наши точки визуально, наша следующая задача состоит в том, чтобы разделить эти точки с помощью линии, и именно здесь появляется термин граница решения.

Граница решения является основным разделителем для разделения точек на соответствующие классы.

(Как и почему я говорю, что основной разделитель, а не просто любой разделитель, мы рассмотрим, понимая математику)

Уравнение гиперплоскости :

Уравнение главной разделительной линии называется уравнением гиперплоскости.

 

 

 

Давайте посмотрим на уравнение прямой с наклоном m и точкой пересечения c.

Уравнение принимает вид: mx + c = 0

(Обратите внимание: мы поместили прямую/линейную линию, которая является 1-мерной, в 2-мерном пространстве)

 

 

Уравнение гиперплоскости, разделяющее точки (для классификации), теперь может быть легко записано как:

H: w ^T (x) + b = 0

Здесь: b = член пересечения и смещения уравнения гиперплоскости

В D-мерном пространстве гиперплоскость всегда будет оператором D-1.

Например, для двумерного пространства гиперплоскость — это прямая линия (одномерная).

 

2.3 Измеритель расстояния

Теперь, когда мы увидели, как представлять точки данных и как провести разделительную линию между точками. Но при подгонке разделительной линии мы, очевидно, хотели бы такую ​​линию, которая могла бы наилучшим образом разделить точки данных с наименьшим количеством ошибок/ошибок промаха классификации.

Таким образом, чтобы иметь наименьшие ошибки в классификации точек данных, эта концепция требует, чтобы мы сначала знали расстояние между точкой данных и разделительной линией.

 

Расстояние любой линии, ax + by + c = 0, от заданной точки, скажем, (x ₀ , y ₀ ) определяется как d.

Аналогично, расстояние уравнения гиперплоскости: w ^T Φ(x) + b = 0 от заданного точечного вектора Φ(x ₀ ) можно легко записать как:

здесь ||w||2 — евклидова норма длины w, определяемая как:

 

[stextbox id=’alert’ shadow=”false”] Теперь, когда термины понятны, давайте углубимся в алгоритм, используемый позади. [/stextbox]

 

3. Рыбы много

Математика в море

 

 

3.1 Фон

Мы говорили о примере дифференциации полов, поэтому такие задачи называются задачами классификации. Теперь проблема классификации может иметь только два (двоичных) класса для разделения или может иметь более двух, что известно как проблемы классификации с несколькими классами.

Но не все прогностические модели классификации поддерживают многоклассовую классификацию, такие алгоритмы, как логистическая регрессия и машины опорных векторов (SVM), были разработаны для двоичной классификации и изначально не поддерживают задачи классификации с более чем двумя классами.

Но если кто-то все еще хочет использовать алгоритмы бинарной классификации для задач множественной классификации, один из широко используемых подходов состоит в том, чтобы разбить наборы данных мультиклассовой классификации на несколько наборов данных бинарной классификации, а затем подобрать модель бинарной классификации для каждого из них.

Двумя различными примерами этого подхода являются стратегии «Один против остальных» и «Один против одного». О двух подходах можно прочитать здесь.

Двигаясь вперед к основной теме понимания математики, мы будем рассматривать проблему классификации двоичных классов по двум причинам:

1. Как уже упоминалось выше, SVM работает намного лучше для бинарного класса
2.  Было бы легко понять математику, поскольку наша целевая переменная (переменная / невидимые данные, предназначенные для прогнозирования, является ли точка мужчиной или женщиной)
3. Примечание. Это будет подход «один против одного».

3.1.1 Случай 1: (Идеальное разделение для двоичных классифицированных данных) –

Продолжая наш пример, если гиперплоскость сможет идеально различать самцов и самок, не делая ошибок при классификации, тогда этот случай разделения известен как идеальное разделение.

Здесь, на рисунке, если самцы зеленые, а самки красные, и мы можем видеть, что гиперплоскость, которая здесь является линией, прекрасно различает два класса.

 

Обобщая, данные имеют две классификации , положительную и отрицательную группу , и полностью разделимы, что означает, что гиперплоскость может точно разделить *тренировочные классы*.

**

( Обучающие данные — Данные, с помощью которых алгоритм/модель изучает шаблон того, как различать, просматривая признаки данные, где даны только признаки, и теперь модель скажет самец это или самка)

 

**

Теперь может быть много гиперплоскостей, дающих 100% точность, как видно на фотографии.

«» Итак, чтобы выбрать оптимальную/наилучшую гиперплоскость, поместите гиперплоскость прямо в центр, где максимальное расстояние от ближайших точек и далее дайте наименьшие ошибки теста. «»

 Обратите внимание: мы должны стремиться к наименьшему количеству ошибок ТЕСТА, а НЕ к ошибкам ОБУЧЕНИЯ. 

 

Итак, мы должны максимизировать расстояние, чтобы дать некоторое пространство уравнению гиперплоскости, которое также является целью/основной идеей SVM.

Цель алгоритма SVM:

Итак, теперь нам нужно:

Нахождение гиперплоскости с максимальным запасом (зазор — это в основном защищенное пространство вокруг уравнения гиперплоскости), и алгоритм пытается получить максимальный запас с ближайшими точками (известными как опорные векторы).

Другими словами, “ Цель состоит в том, чтобы максимизировать минимальное расстояние. ”  для расстояния (упомянутого ранее в разделе 2)

, предоставлено:

Итак, цель понятна. Делая прогнозы на обучающих данных, которые были бинарно классифицированы как положительные и отрицательные группы, если точка заменена положительной группой в уравнении гиперплоскости, мы получим значение больше 0 (ноль). Математически,

w ^T ( Φ(x)) + b > 0

И предсказания из отрицательной группы в уравнении гиперплоскости дадут отрицательное значение как

w ^T ( Φ(x)) + b < 0.  

Но здесь знаки были об обучающих данных, именно так мы обучаем нашу модель. Что для положительного класса дайте положительный знак, а для отрицательного — отрицательный.

Но при тестировании этой модели на тестовых данных, если мы правильно предсказываем положительный класс (положительный знак или знак больше нуля) как положительный, то два положительных результата дают положительный и, следовательно, результат больше нуля. То же самое применимо, если мы правильно предсказываем отрицательную группу, поскольку два отрицательных значения снова дадут положительный результат.

Но если ошибка модели классифицирует положительную группу как отрицательную группу, тогда один плюс и один минус составляют минус, следовательно, в целом меньше нуля.

Подводя итог вышеизложенному:

Произведение предсказанной и фактической метки будет больше 0 (ноля) при правильном предсказании, в противном случае меньше нуля.

 

Для идеально разделимых наборов данных оптимальная гиперплоскость правильно классифицирует все точки, дополнительно заменяя оптимальные значения в весовом уравнении.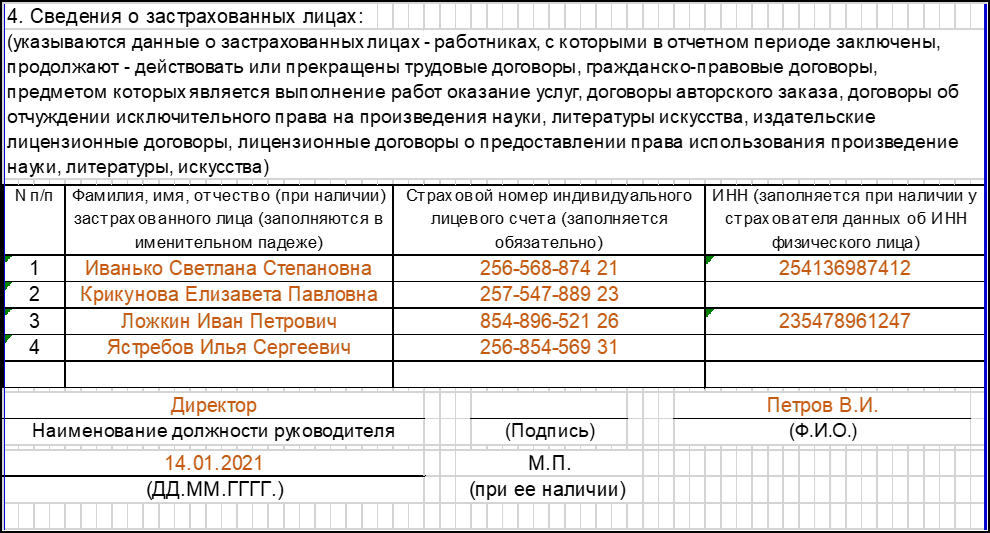

Здесь :

arg max — это аббревиатура для аргументов максимумов, которые в основном являются точками области определения функции, в которых значения функции максимальны.

(Для дальнейшей работы с arg max в машинном обучении читайте здесь.)

Далее, выведение независимого члена веса наружу дает:

 

 

Внутренний член (мин _n y _n |w ^T Φ(x) + b | ) в основном представляет собой минимальное расстояние точки до границы решения и ближайшую точку к границе решения H.

Изменение масштаба расстояния до ближайшей точки как 1 т.е. (min _n y _n |w ^T Φ(x) + b |) = 1. Здесь векторы остаются в одном направлении и уравнение гиперплоскости не изменится. Это похоже на изменение масштаба изображения; объекты расширяются или сжимаются, но направления остаются прежними, и изображение остается неизменным.

Изменение масштаба расстояния осуществляется путем подстановки,

Уравнение теперь становится (описывая, что каждая точка находится на расстоянии не менее 1/||w||2 от гиперплоскости) как

Эта задача на максимизацию эквивалентна следующей задаче на минимизацию, которая умножается на константу, поскольку они не влияют на результаты.

3.1.2 Первичная форма SVM (полное разделение):

Вышеупомянутая задача оптимизации является первичной формулировкой, поскольку в постановке задачи есть исходные переменные.

3.2 СЛУЧАЙ 2: (не идеальное разделение)

Но все мы знаем, что не бывает ситуации, когда все идеально, а что-то всегда идет наоборот.

В нашем примере гендерной классификации мы не можем ожидать, что модель даст такое уравнение гиперплоскости, которое идеально разделит оба пола, всегда будет одна или несколько точек, которые не попадут в свою категорию, в то время как оптимальная гиперплоскость уравнение подходит, известное как классификация промахов. (Как показано на изображении ниже)

 

Таким образом, мы не можем ожидать идеального/идеального корпуса. Здесь мы становимся умнее модели и позволяем модели сделать несколько ошибок при классификации точек и, следовательно,

И, следовательно, добавьте резервную переменную в качестве штрафа за каждую неудачную классификацию для каждой точки данных, представленной β (бета). Таким образом, отсутствие штрафа означает, что точка данных правильно классифицирована, β = 0, и при любой классификации промахов β > 1 в качестве штрафа.

3.2.1 Первичная форма SVM (неидеальное разделение):

Здесь: для β и C

Slack для каждой переменной должен быть как можно меньше и дополнительно регулироваться гиперпараметром C

Приведенное выше уравнение является примером выпукло-квадратичной оптимизации , поскольку целевая функция квадратична по W, а ограничения линейны по W и β.

Раствор для первичной формы : (не идеальное разделение):

Так как у нас есть Φ, который имеет комплексное обозначение. мы бы переписали уравнение.

Концепция

 в основном состоит в том, чтобы избавиться от Φ и, следовательно, переписать основную формулировку в двойной формулировке, известной как двойная форма проблемы, и решить полученную задачу оптимизации ограничений с помощью метода множителя Лагранжа. 

Другими словами:

Двойная форма: переписывает ту же задачу, используя другой набор переменных. Таким образом, альтернативная формулировка поможет устранить зависимость от Φ, а уменьшение эффекта будет выполнено с помощью Kernelization.

Метод множителя Лагранжа: Это стратегия поиска локальных минимумов или максимумов функции при условии, что одно или несколько уравнений должны точно удовлетворяться выбранными значениями переменных.

Кроме того, формальное определение двойственной задачи может быть определено как:

Двойственная лагранжева задача получается путем формирования сначала лагранжиана уже полученной задачи минимизации с помощью множителя Лагранжа, чтобы к целевой функции можно было добавить новые ограничения , а затем будет решаться для значений первичной переменной , которые минимизируют исходную целевую функцию

.

Это новое решение делает основные переменные функциями множителей Лагранжа и называется двойственными переменными, так что новая задача состоит в том, чтобы максимизировать целевую функцию для двойственных переменных с новыми производными ограничениями.

В этом блоге очень хорошо объясняется работа множителей Лагранжа.

Возьмем пример применения множителя Лагранжа   для лучшего понимания того, как преобразовать основную формулу с использованием множителей Лагранжа для решения задачи оптимизации .

Ниже x — исходная основная переменная и минимизация функции f при наборе ограничений, заданном g, и переписывание для нового набора переменных, называемых множителями Лагранжа.

Решение простых переменных путем дифференцирования Лагранжа без ограничений.

И, наконец, обратная подстановка в уравнение Лагранжа и переписывание ограничений

  Вернемся к нашей первичной форме:  

Шаг 1: Получение прямого числа и определение лагранжевой формы из простого числа

Шаг 2: Получение решения путем представления простого числа в форме двойственного числа

Шаг 3: Подставить полученные значения в лагранжеву форму

Окончательная двойная форма из приведенного выше упрощения:

Вышеупомянутая двойная форма все еще имеет Φ термов, и здесь это легко решается с помощью Kernelization

Ядро по определению избегает явного отображения, необходимого для получения алгоритмов линейного обучения для изучения нелинейной функции или границы решения Для всех x и x’ во входном пространстве Φ некоторые функции k(x,x’) могут быть выражены как скалярный продукт в другом пространстве Ψ. Функция

упоминается как Ядро . Короче говоря, для машинного обучения ядро ​​определяется как записанное в виде «карты функций»

который удовлетворяет

Для лучшего понимания ядер можно обратиться к этой ссылке квора

  Ядро имеет два свойства:  

•  Он симметричен по своей природе k(x  n  , x  m  ) = k(x  m  , x  n  ) 

•  Положительный полуопределенный 

Чтобы иметь представление о работе ядер, может быть полезна эта ссылка квора.

По определению ядра мы можем подставить эти значения

Итак, подставив свойства ядра и по определению ядра в нашу двойственную форму,

Мы получаем Новое уравнение как:

И это решение не содержит Φ, и его гораздо проще вычислить. и это была математика, стоящая за моделью SVM.