Внутренняя норма доходности инвестиционного проекта: Внутренняя норма доходности. Формула расчета IRR инвестиционного проекта.
Внутренняя норма доходности (IRR, ВНД): что это такое, формула
Внутренняя норма доходности (IRR – Internal Rate of Return) – показатель, который занимает важное место в финансовом анализе и используется обычно для расчета рентабельности и прибыльности любого инвестиционного проекта, независимо от сферы, вида, вкладываемых сумм и т.д.
Под IRR проекта понимают величину ставки дисконта, при достижении которой общая сумма вложений в проект (денежные потоки или чистая приведенная стоимость, что обозначается как NPV) равна нулю.
То есть, если значение IRR получается 0, то инвестор просто возвращает свои средства, если меньше – проект приносит убыток, больше – прибыль.
Расчет IRR обычно используется не столько для вычисления прибыльности конкретного проекта (для этого есть другие, более эффективные и наглядные, методы), сколько для сравнения показателей нескольких проектов. Так, когда речь идет о разных видах инвестирования с совершенно разными суммами и частотой денежных вливаний, порой трудно понять, какой вариант приносит больше чистого дохода. Именно внутренняя норма доходности проекта позволяет сразу видеть, что выгоднее и эффективнее.
Именно внутренняя норма доходности проекта позволяет сразу видеть, что выгоднее и эффективнее.
Перед тем, как выполнять расчет IRR, сначала считают NPV (приводят общую сумму инвестиций к цене «на сегодня»), а после уже высчитывают норму доходности. Другие названия IRR – внутренняя ставка доходности, внутренняя норма дисконта, коэффициент эффективности (окупаемости), иногда называют просто «внутренняя норма».
Оба показателя – IRR и NPV – рассматриваются в качестве взаимодополняющих критериев, важных для осуществления оценки эффективности реализации инвестиционного проекта.
Что это такое IRR инвестиционного проекта простыми словами и зачем он нужен
С английского языка термин Internal Rate of Return (аббревиатурой которого является IRR) переводится как «внутренняя ставка возврата». Такое название проще и доступнее всего характеризует показатель. Норма доходности инвестиционного проекта внутренняя представляет собой такую ставку прибыльности, при которой достигается дисконтированная самоокупаемость.
Все денежные потоки проекта делятся на две группы: это входящие потоки со знаком плюс (прибыль от коммерческой деятельности) и потоки исходящие со знаком минус (все затраты на реализацию проекта, вложения). Получается, чтобы проект вообще был запущен, эти два вида финансовых потоков в итоге должны давать 0. То есть, расходы должны компенсироваться доходами, если же показатель меньше, проект считается убыточным и себя не окупит, если больше – прибыльным.
Как было указано выше, обычно уровень прибыльности конкретного проекта высчитывают другими методами и все данные есть в бизнес-плане. А вот когда речь идет о двух разнотипных проектах, есть смысл найти и рассчитать IRR для всех, а потом просто сравнить цифры.
Тут важно помнить про то, что самоокупаемость должна быть именно «дисконтированной» — такой, которая учитывает различные процентные ставки, работающие в течение периода инвестирования (это могут быть ставки процентные в банке, уровень девальвации, индекс инфляции и т. д.).
д.).
Расчет ВНД позволяет учитывать специальный поправочный коэффициент – ставку дисконта, которая демонстрирует уровень эффективности использования капитала в сравнении с иными вариантами вложений в бизнес за аналогичный временной отрезок.
Основные цели расчета внутренней нормы доходности:
- Оценка прибыльности инвестиции – чем больше будет показатель в числовом выражении, тем более доходным и успешным считается проект.
- Определение максимальных годовых ставок при условии привлечения заемного капитала (особенно если речь идет о займах у банка: так, если ставка процентная выше рентабельности, проект будет убыточным).
- Сравнение нескольких проектов, предполагающих разные денежные вливания, поэтапные инвестиции, отличающиеся сроки, уровни прибыли и т.д.
Как рассчитать правильно показатель IRR
Разобравшись с тем, что такое IRR инвестиционного проекта, стоит рассмотреть, как его можно посчитать. Методов расчета существует несколько – с использованием формулы или таблицы Excel, а также графический способ. Можно найти в Интернете и специальные калькуляторы, в которые просто нужно внести значения и получить искомый показатель.
Методов расчета существует несколько – с использованием формулы или таблицы Excel, а также графический способ. Можно найти в Интернете и специальные калькуляторы, в которые просто нужно внести значения и получить искомый показатель.
Формула и пример расчета в экономике
Для расчета IRR формула исходная представлена в виде уравнения:
Тут:
- NPV – это чистая приведенная стоимость рассматриваемого проекта.
- N – число расчетных периодов (лет чаще всего).
- T – номер конкретного расчетного периода.
- IS – расходы на проект первоначальные (стартовые инвестиции) и последующие.
- IRR – внутренняя норма доходности.
Предельно низкая ВСД равна значению NPV, соответствующему нулю. То есть, текущая стоимость, посчитанная по ставке прибыльности IRR, должна быть равной самоокупаемости. Благодаря преобразованиям формулы можно отыскать минимальный показатель IRR:
Тут:
- IRRmin – минимальное значение
- N – число расчетных периодов.

- IST – величина инвестиций каждого периода.
- IS – общее число инвестиций.
Расчет в таблице Excel
Когда рассчитывается внутренняя норма доходности, формула используется далеко не всегда. Посчитать внутреннюю норму рентабельности можно и в Excel, где есть встроенная функция ВСД.
Как рассчитывается средняя норма рентабельности в Excel:
- Вход в программу.
- Создание книги с указанием таблицы денежных потоков, дат. Одно значение должно иметь отрицательный показатель (это сумма вложений). Таблица может включать информацию про множество проектов, если их нужно сравнить.
- Далее осуществляется выбор функции IRR (русский интерфейс обозначает его как ВСД либо ВНД), потом нужно нажать fx.
- Отметка участка нужного столбца со всеми данными, которые планируется проанализировать. В строке должно появиться что-то типа IRR(B4:В:15.2, 7.1%). Нажать на «ОК».
Графический метод определения IRR
Для поиска показателя используется не только формула расчета, но и графический метод. Он более наглядный, но и менее точный. Чтобы построить диаграмму, нужно выполнить определенные вычисления, но тут требования по точности гораздо ниже. Да и исходные данные могут давать погрешность.
Он более наглядный, но и менее точный. Чтобы построить диаграмму, нужно выполнить определенные вычисления, но тут требования по точности гораздо ниже. Да и исходные данные могут давать погрешность.
Недостатки внутренней нормы доходности заемных средств – SPRINTinvest.RU
Мне не терпится еще раз вернуться к теме внутренней нормы доходности, которую мы довольно лихо распотрошили в прошлый раз.
Сегодня мы обратим внимание на некоторые нюансы, могущие иметь место на практике, которые явно укажут на сферы, где попытки опереться на внутреннюю норму доходности не только не принесут нам никакой пользы, но заведомо приведут к явно проигрышным решениям.
Как мы помним, применение внутренней нормы доходности эффективно в ситуациях, когда при росте ставки дисконтирования происходит равномерное уменьшение чистой приведенной стоимости соответствующих денежных потоков.
В действительности так происходит далеко не всегда, чему свидетельством могут служить многочисленные примеры.
Недостатки внутренней нормы доходности
Представим, что перед нами дилемма: вложиться в проект «А», требующий первоначальных инвестиций в размере 850 долл. и гарантирующий через год денежный поток в размере 1275 долл., либо в
Проведя несложные вычисления, мы увидим, что внутренняя норма доходности (IRR) для обоих проектов одинакова и составляет +50 %.
Это очевидно, если решить два примера с нашими исходными данными: [1] для проекта «А»: -850 долл. + 1275 долл. / (1 + IRR) = 0; [2] для проекта «Б»: 850 долл. — 1275 долл. / (1 + IRR) = 0; оба равенства окажутся истинными при IRR = 0,5.
Можно ли с учетом наших условий признать проекты «А» и «Б» равнозначными в плане инвестиционной привлекательности?
Ответ однозначен: НЕТ, НЕТ и еще раз НЕТ!
В проекте «А» мы фактически выступаем в роли кредитора, предоставляя потребителю деньги в долг по ставке 50 %.
В проекте «Б» наша роль прямо противоположна: мы берем деньги взаймы под 50 %, фактически являясь должниками.
В первом случае нам будет выгодна высокая доходность, во втором – низкая…
Для пущей убедительности построим график зависимости чистой приведенной стоимости от величины ставки дисконтирования для наших проектов, аналогичный тому, который мы рисовали в прошлый раз.
У нас получится примерно такая картина:
С графиком для проекта «А» все ясно: он являет собой классическую ситуацию, в которой допустимо применение метода внутренней нормы доходности.
Здесь чистая приведенная стоимость имеет положительные значения, когда ставка дисконтирования колеблется в пределах от 0 до 0,5.
Этот диапазон отражает множество альтернативных издержек, размер которых МЕНЬШЕ нашей внутренней нормы доходности.
С графиком для проекта «Б» все обстоит совсем не так. Чистая приведенная стоимость здесь окажется положительной, когда ставка дисконтирования будет варьироваться в диапазоне от 0,5 до 1,0.
Именно в этом диапазоне расположено множество альтернативных издержек и именно здесь нам придется искать приемлемый вариант для инвестиций.
Но есть тот самый пресловутый «один нюанс»: внутренняя норма доходности при таком раскладе оказывается МЕНЬШЕ альтернативных издержек.
Если следовать правилу внутренней нормы доходности в этой ситуации, нам – в нарушение классических принципов инвестирования — придется ориентироваться на инвестиции, обеспечивающие доходность НИЖЕ альтернативных издержек.
Пример 2-ой, жизненный
Первого примера вполне могло оказаться достаточным. Но мы рассмотрим тему еще глубже.
Исходные данные нового примера таковы: пусть нас заинтересовал проект «В», для инвестиций в который мы сначала одалживаем 1000 долл., после первого года дополнительно инвестируем 3400 долл., затем (после второго года) получаем возврат инвестиций в сумме 4200 долл., еще через год инвестируем в проект 1850 долл.
Нулевого значения чистой приведенной стоимости в данном примере можно добиться при IRR = 0,14 (14 %).
Будет ли это означать, что если на рынке присутствуют альтернативные издержки, равные, скажем, 7%, то мы должны будем принять инвестиции в проект «В»?
На самом деле проект «В» сочетает в себе черты и проекта «А», и проекта «Б», которые мы рассмотрели ранее.
В одни периоды мы ведем себя как кредиторы, в другие – как должники.
Если при ответе на сформулированный вопрос полагаться исключительно на внутреннюю норму доходности, можно легко прийти к неверным выводам.
В этой ситуации наиболее оптимальным следует признать использование формул расчета чистой приведенной стоимости.
Строим график для проекта «В». Он будет иметь примерно такой вид:
Из этого графика легко узнаваема тенденция к росту чистой приведенной стоимости вслед за ростом ставки дисконтирования.
При этом положительные значения чистой приведенной стоимости сконцентрированы в диапазоне от 0,14 до 1,00.
Окончательный вердикт таков: несмотря на то, что внутренняя норма доходности проекта «В» составляет 14%, при наличии на рынке альтернативных издержек, равных 7%, мы должны будет ОТКАЗАТЬСЯ от инвестиций в проект «В».
Вот так-то и никак не иначе…
Заключение
Приведенные выше примеры дают определенную ясность относительно того, что когда мы для наших инвестиций используем заимствованные денежные средства, возможны ситуации, при которых в процессе обоснования инвестиционных решений полагаться исключительно на значения внутренней нормы доходности нельзя…
При этом на выручку к нам придет уже не раз доказавший свою жизнеспособность метод расчета чистой приведенной стоимости.
Этим круг ситуаций, в которых внутренняя норма доходности оказывается «бессильной», не исчерпывается.
Развитие темы обязательно последует в наших скорых публикациях. Будет немало интересного. Удачи!
Внутренняя Норма Доходности Инвестиционного Проекта Irr :: ИНВЕСТОРОВ.НЕТ
Определение «инвестиции» — довольно емкое понятие. Можно вложить свободные деньги в депозит на банковский счет, чтобы получить дополнительный доход, или приобрести акции того же банка, компании. Это наиболее доступный, но не особо доходный способ. И совершенно другая история – капиталовложения в бизнес, когда владелец денежных средств покупает долгосрочные активы, обеспечивая себе в будущем дополнительные финансовые потоки по результатам деятельности инвестиционного проекта.
И совершенно другая история – капиталовложения в бизнес, когда владелец денежных средств покупает долгосрочные активы, обеспечивая себе в будущем дополнительные финансовые потоки по результатам деятельности инвестиционного проекта.
Основной задачей, вложенных в дело, денег служит возможный доход от деятельности организации, предприятия, компании. Но не всегда это требование выполняется. Эффективность инвестиций определяется степенью соответствия проекта поставленным целям людей, принимающих участие в таком мероприятии.
Оценка предполагаемых результатов деятельности, в которую совершаются инвестиции, имеет важное значение при принятии решения о долгосрочном спонсировании любого проекта. Для этого необходимо владеть подробной информацией, которая дает представление о:
- имеющихся гарантиях надежности вклада и степени вероятности их возврата в будущем;
- возможности получить прибыль, которая способна компенсировать воздержание от использования собственных средств в течение периода реализации проекта.

Возможности оценки инвестиционных проектов
Для понимания и анализа проекта, в который предполагается денежное сложение, инвестору необходимы все данные о разработанных планах и имеющихся возможностях выполнения поставленных задач. Это позволить получить представление о реально существующих рисках, эффективности запланированного предприятия, его перспективах и принять решение о целесообразности внесения капитала.
Существует несколько стандартов оценки проектов, но к числу основных принято относить два, тесно взаимосвязанных, – финансовый и экономический параметры. И если первый предполагает подробное изучение ликвидных возможностей и платежных, то в экономическом аспекте рассматривается, главным образом, вероятная способность проекта не потерять ценностных характеристик инвестиционных средств.
Простая норма прибыли и период окупаемости вложений – прерогатива статистического подхода к рассмотрению будущности созданного плана мероприятий. Наиболее точными методами анализа проекта служат динамические исследования, но при условии наличия полной и достоверной информации. Если получить таковую в полном объеме не получается, то данный критерий подвергается модификации.
Если получить таковую в полном объеме не получается, то данный критерий подвергается модификации.
Внутренняя норма доходности и с чем ее «едят»
Внутренняя норма доходности инвестиционного проекта – это процентная ставка, приводящая размер финансовых потоков данного проекта к нулю. Другими словами, при соблюдении таких условий, инвестор имеет все шансы на возмещение вложенных средств в первоначальном их объеме, и не больше. Обозначается такой показатель в виде индекса «ВНП» или «NPV», и рассчитать его можно по общепринятой формуле в виде математического выражения:
где
i – дисконтставка;
CFt – платеж, который зависит от периода времени «t»;
IC – стартовая инвестиция равная -CF0.
Чтобы не допустить досадной ошибки и вернуть свои инвестиции с приростом и следует провести расчет NPV, который с наибольшей точностью способен определить чистый дисконтированный доход. Алгоритм расчета будет следующим:
- оценка денежных потоков – вложенные средства и ожидаемые финансовые притоки в процессе работы проекта;
- определение стоимости собственного капитала, что послужит дисконтированной ставкой;
- проанализировать все денежные потоки по дисконтставке;
- сложить полученные результаты, сумма которых и составит ВНП проекта.

В случае, когда искомый показатель выше нуля, можно смело инвестировать средства, но если он выражается в отрицательных числах, это означает, что риск потери капиталовложений имеет большую вероятность.
Логика обоснования NPV
Все предельно просто: когда индекс NPV доходит до нуля – это сигнал, что вклад финансов в предстоящее дело будет успешным, и вероятность в будущем вернуть свои вложения с прибылью достаточно реальна. А если этот показатель поднимается выше, то сомнений по отношению к успешности проекта оставаться не может.
Положительный NPV означает прибыльность задуманного мероприятия, и чем выше его значения, тем выше будет получаемая прибыль. Доход кредиторов, предоставивших свою помощь, остается фиксированным, а потому все что идет выше – собственность акционеров. Если разработанный проект утверждается с нулевым показателем внутренней нормы доходности, то инвесторы остаются на прежних позициях при увеличении компании, но неизменной цене на акции.
Но математическая формула дает формальное понимание нескольких величин. Чтобы наглядно убедиться в важности показателя NPV, рассмотрим на примере показатели двух проектов, действующих в течение четырех лет.
Порядковый № года | 1-й проект | 2-й проект |
0 | 10000 | 10000 |
1 | 5000 | 2000 |
2 | 5000 | 3000 |
3 | 4000 | 4000 |
4 | 2000 | 6000 |
Из приведенной выше таблицы видно, что при одинаковом инвестиционном старте обоих проектов в 10000, денежные потоки в разные годы значительно разняться. В первом случае предполагается отдача вложенных средств в ближайшие годы, но затем ожидается резкий их спад. Второй же проект показывает незначительный рост потоков в начале своей деятельности, но далее последует активный рост доходной части.
В первом случае предполагается отдача вложенных средств в ближайшие годы, но затем ожидается резкий их спад. Второй же проект показывает незначительный рост потоков в начале своей деятельности, но далее последует активный рост доходной части.
Все вышесказанное справедливо при условии стандартного инвестирования, но когда финансирование запланированного комплекса мероприятий предполагает реинвестирование прибыли, тут возникает большая вероятность значительных искажений индекса внутренней нормы доходности. Урегулировать данную положение следует введением еще одного показателя – модифицированной нормы доходности инвестиций.
Общим недостатком обоих видов норм доходности считается сложность получения конкретных данных при денежных потоках в отличных валютах в разные временные периоды. Осложнения возникают и при расчетах с изменениями ставки рефинансирования в течение работы проекта.
Понятие внутренней нормы доходности проекта и методика ее расчета — Студопедия
Ставка доходности проектов
PI= 851/100 = 85,1%
Или по второму варианту PI =1851/1000 = 1,85
Ставка доходности проекта показывает величину прироста активов от реализации проекта на единицу инвестиций. В данном примере индекс доходности проекта больше единицы. Это подтверждает, что величина NPV больше нуля.
В данном примере индекс доходности проекта больше единицы. Это подтверждает, что величина NPV больше нуля.
При принятии инвестиционных решений аналитики отдают предпочтение показателю PI в том случае, если величина NPV в рассматриваемых проектах одинакова. Показатель NPV является абсолютным, поэтому возможна ситуация, когда проекты будут иметь равную чистую текущую стоимость доходов.
Пример. Предположим, аналитик должен выбрать один из двух предложенных проектов.
Проект Х требует инвестирования в сумме 900, поток доходов: первый год – 300, второй год – 400, третий год – 600.
Проект У требует затрат в сумме 325 и обеспечит доходы: первый год – 100, второй год – 200, третий год – 300.
Ставка дисконтирования, используемая при принятии решения – 10%.
Расчет показателя NPV
| Показатель | Проект Х | Проект Y |
| Суммарный приведенный доход | ||
| Затраты по проекту | ||
| NPV | +155 | +157 |
Величина чистой текущей стоимости доходов по анализируемым проектам существенно не отличается. Для отбора проекта целесообразно использовать ставку доходности проекта:
Для отбора проекта целесообразно использовать ставку доходности проекта:
Проект Х PI = 155*100%/900 = 17,2%
Проект Y PI = 157*100%/325 = 43,2%
Для инвестора более выгодным является проект Y, т. к. он имеет ставку доходности в 2,5 раза больше.
Преимущества показателяPI заключаются в том, что он является относительным и отражает эффективность единицы инвестиций. Кроме того, в условиях ограниченности ресурсов этот показатель позволяет сформировать наиболее эффективный инвестиционный портфель.
Основным недостатком является зависимость результатов расчета от ставки дисконтирования.
Внутренняя норма доходности проекта (IRR) – это ставка дисконтирования, приравнивающая сумму приведенных доходов от проекта к величине инвестиций (затрат), т.е. при которой NPV=0.
Этот метод оценки инвестиционных проектов основан на определении максимальной величины ставки дисконтирования, при которой проект останется безубыточным.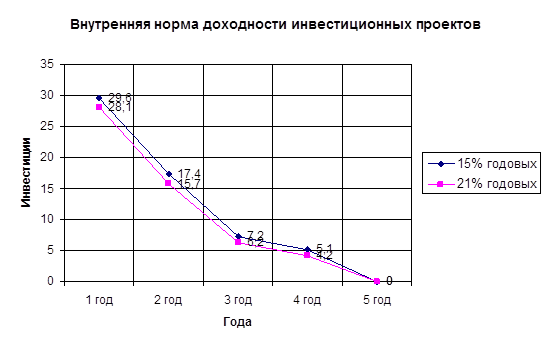
Методика расчета IRRбез финансового калькулятора достаточно трудоемка, в ее основе лежит метод интерполяции. Расчет осуществляется следующим образом:
1.Выбирается произвольная ставка дисконтирования и на ее основе рассчитывается NPV.
2.Если первоначальная произвольная ставка дисконтирования не дает нулевого NPV, то выбирается вторая ставка дисконтирования по следующему правилу:
если NPV > 0, то новая ставка дисконтирования должна быть больше первоначальной;
если NPV < 0, то новая ставка дисконтирования должна быть меньше первоначальной.
3.Подбор второй ставки дисконтирования следует проводить до тех пор, пока не получим NPV>0 и NPV<0. (рекомендации: поскольку близость произвольно выбираемых ставок дисконтирования к искомой IRR существенно не влияет на точность расчетов, то при подборе ставок дисконтирования целесообразно увеличить интервал. Например, если первая ставка дисконтирования 6%, то вторая может быть 18 или 22%)
4. Рассчитаем внутреннюю ставку доходности проекта методом интерполяции.
Рассчитаем внутреннюю ставку доходности проекта методом интерполяции.
IRR=r1+ NPV1*(r2-r1) / (NPV1-NPV2)
Где
r1 – ставка дисконтирования при которой NPV1>0
r2 – ставка дисконтирования при которой NPV2<0
По методике, приведенной ранее, рассчитаем IRR по проекту «Уран».
NPV при ставке дисконтирования 35% = 108, а при ставке дисконтирования 45% = -106.
Т.о., r1 = 35%, NPV1 =108
r2 = 45%, NPV2 = -106
IRR = 35% + 108*(45%-35%) / (108 –(-106)) = 40,05%
Предпочтение обычно отдается проекту, имеющему наибольшую величину данного показателя. Использование IRR при анализе и отборе инвестиционных проектов основано на интерпретации этого показателя. IRR является индивидуальным показателем конкретного проекта, представленного не только данной суммой затрат, но и потоком доходов, индивидуальным как по величине, так и по времени возникновения.
Рассмотрим влияние распределения доходов во времени на показательIRR.
| Показатель | Проект I | Проект II | Проект III |
| Затраты: | (1200) | (1200) | (1200) |
| первый год | |||
| второй год | |||
| третий год | |||
| IRR | 12% | 16% | 10% |
Все три проекта требуют одинаковых затрат, совпадает и сумма доходов, в том виде, в каком они будут представлены в финансовых отчетах соответствующих лет. Однако различия в распределении потока доходов во времени оказывает существенное влияние на показатель IRR. Внутренняя ставка доходности проекта II почти в 1,6 раза выше, чем по проекту III.
IRR можно интерпретировать как некий «запас прочности» проекта, отражающий его устойчивость в условиях возможного повышения риска. Неблагоприятные изменения, затрагивающие как экономику в целом, так и конкретный вид бизнеса, требует адекватного уровня ставки дисконтирования.
Проекты с максимальной величиной IRR более привлекательны, т. к. потенциально способны выдерживать большие нагрузки на инвестиционный капитал, связанные с возможным повышением его стоимости.
Возможен другой подход к интерпретации IRR, которая в этом случае рассматривается как максимальная ставка по кредиту.
Расчет показателейIRR в мировой практике инвестиционного анализа является важным этапом. Сравнение расчетной величины IRR с требуемой нормой дохода на капитал в данной конкретной сфере позволяет на начальной стадии отклонять неэффективные проекты. Тем не менее методу оценки проектов, основанному на сравнении IRR, присущи недостатки:
Во-первых, показатель IRR сложно использовать для оценки инвестиционного портфеля в целом, т. к. он, в отличие от показателя NPV, не суммируется и характеризует только конкретный проект.
Во-вторых, показатель IRR требует особого применения при анализе проектов, имеющих несколько крупных отрицательных денежных потоков в течение экономической жизни проекта.
В следствии неоднократного инвестирования, чистая текущая стоимость доходов будет принимать нулевое значение несколько раз. Следовательно, IRR будет иметь столько же решений. Для анализа рекомендуется использовать минимальное значение внутренней ставки доходности проекта.
Проблема ранжирования инвестиционных проектов на основе показателей IRRи NPV может проявляться в двух основных ситуациях:
1. При выборе из двух альтернативных проектов один из них может иметь лучшие показатели как по NPV, так и по IRR.
Графически это выглядит следующим образом.
В данном случае проект Б имеет большую величину NPV и IRR, что делает его безусловно более привлекательным.
2. При выборе из двух альтернативных проектов один может иметь большую часть NPV, другой большее значение IRR, графически это представляется так:
Проект А имеет лучшее значение NPV, проект Б обеспечивает большую часть IRR. Существует некоторая ставка дисконтирования – Х, которая уравнивает по проектам А и Б значение NPV. Эта ставка дисконтирования является критической точкой, меняющей привлекательность оцениваемых проектов:
— если ставка дисконтирования, применяемая аналитиком, меньше этого критического значения, то более привлекательным является проект А;
— если ставка дисконтирования, оценивающая риск вложений в данный объект собственности, больше критической величины, то инвестиционная привлекательность объектов меняется, и более выгодным становится объект Б.
Чистая приведенная стоимость NPV (ЧПС) и внутренняя ставка доходности IRR (ВСД) в EXCEL
Рассчитаем Чистую приведенную стоимость и Внутреннюю норму доходности с помощью формул MS EXCEL.
Начнем с определения, точнее с определений.
Чистой приведённой стоимостью (Net present value, NPV) называют сумму дисконтированных значений потока платежей, приведённых к сегодняшнему дню (взято из Википедии). Или так: Чистая приведенная стоимость – это Текущая стоимость будущих денежных потоков инвестиционного проекта, рассчитанная с учетом дисконтирования, за вычетом инвестиций (сайт cfin. ru) Или так: Текущая стоимость ценной бумаги или инвестиционного проекта, определенная путем учета всех текущих и будущих поступлений и расходов при соответствующей ставке процента. (Экономика . Толковыйсловарь . — М . : » ИНФРА — М «, Издательство » ВесьМир «. Дж . Блэк .)
Примечание1 . Чистую приведённую стоимость также часто называют Чистой текущей стоимостью, Чистым дисконтированным доходом (ЧДД). Но, т.к. соответствующая функция MS EXCEL называется ЧПС() , то и мы будем придерживаться этой терминологии. Кроме того, термин Чистая Приведённая Стоимость (ЧПС) явно указывает на связь с Приведенной стоимостью .
Для наших целей (расчет в MS EXCEL) определим NPV так: Чистая приведённая стоимость — это сумма Приведенных стоимостей денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через равные промежутки времени.
Совет : при первом знакомстве с понятием Чистой приведённой стоимости имеет смысл познакомиться с материалами статьи Приведенная стоимость .
Это более формализованное определение без ссылок на проекты, инвестиции и ценные бумаги, т.к. этот метод может применяться для оценки денежных потоков любой природы (хотя, действительно, метод NPV часто применяется для оценки эффективности проектов, в том числе для сравнения проектов с различными денежными потоками). Также в определении отсутствует понятие дисконтирование, т.к. процедура дисконтирования – это, по сути, вычисление приведенной стоимости по методу сложных процентов .
Как было сказано, в MS EXCEL для вычисления Чистой приведённой стоимости используется функция ЧПС() (английский вариант — NPV()). В ее основе используется формула:
CFn – это денежный поток (денежная сумма) в период n. Всего количество периодов – N. Чтобы показать, является ли денежный поток доходом или расходом (инвестицией), он записывается с определенным знаком (+ для доходов, минус – для расходов). Величина денежного потока в определенные периоды может быть =0, что эквивалентно отсутствию денежного потока в определенный период (см. примечание2 ниже). i – это ставка дисконтирования за период (если задана годовая процентная ставка (пусть 10%), а период равен месяцу, то i = 10%/12).
Примечание2 . Т.к. денежный поток может присутствовать не в каждый период, то определение NPV можно уточнить: Чистая приведённая стоимость — это Приведенная стоимость денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через промежутки времени, кратные определенному периоду (месяц, квартал или год) . Например, начальные инвестиции были сделаны в 1-м и 2-м квартале (указываются со знаком минус), в 3-м, 4-м и 7-м квартале денежных потоков не было, а в 5-6 и 9-м квартале поступила выручка по проекту (указываются со знаком плюс). Для этого случая NPV считается точно также, как и для регулярных платежей (суммы в 3-м, 4-м и 7-м квартале нужно указать =0).
Если сумма приведенных денежных потоков представляющих собой доходы (те, что со знаком +) больше, чем сумма приведенных денежных потоков представляющих собой инвестиции (расходы, со знаком минус), то NPV >0 (проект/ инвестиция окупается). В противном случае NPV
Выбор периода дисконтирования для функции ЧПС()
При выборе периода дисконтирования нужно задать себе вопрос: «Если мы прогнозируем на 5 лет вперед, то можем ли мы предсказать денежные потоки с точностью до месяца/ до квартала/ до года?». На практике, как правило, первые 1-2 года поступления и выплаты можно спрогнозировать более точно, скажем ежемесячно, а в последующие года сроки денежных потоков могут быть определены, скажем, один раз в квартал.
Примечание3 . Естественно, все проекты индивидуальны и никакого единого правила для определения периода существовать не может. Управляющий проекта должен определить наиболее вероятные даты поступления сумм исходя из действующих реалий.
Определившись со сроками денежных потоков, для функции ЧПС() нужно найти наиболее короткий период между денежными потоками. Например, если в 1-й год поступления запланированы ежемесячно, а во 2-й поквартально, то период должен быть выбран равным 1 месяцу. Во втором году суммы денежных потоков в первый и второй месяц кварталов будут равны 0 (см. файл примера, лист NPV ).
В таблице NPV подсчитан двумя способами: через функцию ЧПС() и формулами (вычисление приведенной стоимости каждой суммы). Из таблицы видно, что уже первая сумма (инвестиция) дисконтирована (-1 000 000 превратился в -991 735,54). Предположим, что первая сумма (-1 000 000) была перечислена 31.01.2010г., значит ее приведенная стоимость (-991 735,54=-1 000 000/(1+10%/12)) рассчитана на 31.12.2009г. (без особой потери точности можно считать, что на 01.01.2010г.) Это означает, что все суммы приведены не на дату перечисления первой суммы, а на более ранний срок – на начало первого месяца (периода). Таким образом, в формуле предполагается, что первая и все последующие суммы выплачиваются в конце периода. Если требуется, чтобы все суммы были приведены на дату первой инвестиции, то ее не нужно включать в аргументы функции ЧПС() , а нужно просто прибавить к получившемуся результату (см. файл примера ). Сравнение 2-х вариантов дисконтирования приведено в файле примера , лист NPV:
О точности расчета ставки дисконтирования
Существуют десятки подходов для определения ставки дисконтирования. Для расчетов используется множество показателей: средневзвешенная стоимость капитала компании; ставка рефинансирования; средняя банковская ставка по депозиту; годовой процент инфляции; ставка налога на прибыль; страновая безрисковая ставка; премия за риски проекта и многие другие, а также их комбинации. Не удивительно, что в некоторых случаях расчеты могут быть достаточно трудоемкими. Выбор нужного подхода зависит от конкретной задачи, не будем их рассматривать. Отметим только одно: точность расчета ставки дисконтирования должна соответствовать точности определения дат и сумм денежных потоков. Покажем существующую зависимость (см. файл примера, лист Точность ).
Пусть имеется проект: срок реализации 10 лет, ставка дисконтирования 12%, период денежных потоков – 1 год.
NPV составил 1 070 283,07 (Дисконтировано на дату первого платежа). Т.к. срок проекта большой, то все понимают, что суммы в 4-10 году определены не точно, а с какой-то приемлемой точностью, скажем +/- 100 000,0. Таким образом, имеем 3 сценария: Базовый (указывается среднее (наиболее «вероятное») значение), Пессимистический (минус 100 000,0 от базового) и оптимистический (плюс 100 000,0 к базовому). Надо понимать, что если базовая сумма 700 000,0, то суммы 800 000,0 и 600 000,0 не менее точны. Посмотрим, как отреагирует NPV при изменении ставки дисконтирования на +/- 2% (от 10% до 14%):
Рассмотрим увеличение ставки на 2%. Понятно, что при увеличении ставки дисконтирования NPV снижается. Если сравнить диапазоны разброса NPV при 12% и 14%, то видно, что они пересекаются на 71%.
Много это или мало? Денежный поток в 4-6 годах предсказан с точностью 14% (100 000/700 000), что достаточно точно. Изменение ставки дисконтирования на 2% привело к уменьшению NPV на 16% (при сравнении с базовым вариантом). С учетом того, что диапазоны разброса NPV значительно пересекаются из-за точности определения сумм денежных доходов, увеличение на 2% ставки не оказало существенного влияния на NPV проекта (с учетом точности определения сумм денежных потоков). Конечно, это не может быть рекомендацией для всех проектов. Эти расчеты приведены для примера. Таким образом, с помощью вышеуказанного подхода руководитель проекта должен оценить затраты на дополнительные расчеты более точной ставки дисконтирования, и решить насколько они улучшат оценку NPV.
Совершенно другую ситуацию мы имеем для этого же проекта, е
Показатели эффективности проектов. Модифицированная внутренняя норма рентабельности (MIRR)
Модифицированная внутренняя норма рентабельности – MIRR (ModifiedInternal Rate of Return), %
Как и IRR, MIRR характеризует ставку дисконтирования, при которой суммарная приведенная стоимость доходов равна стоимости инвестиций. Расчет модифицированного значения IRR, для полного понимания, можно разложить по шагам:
1 шаг. Все значения доходов (положительные суммы – притоки, CF+n) приводятся к концу проекта. Для приведения используется ставка, равная средневзвешенной стоимости капитала:
(1+WACC)+(N — n).
2 шаг. Все инвестиции и реинвестиции (отрицательные суммы – оттоки, CF—n) приводятся к началу проекта. Для приведения используется ставка дисконтирования:
(1 + r)-(n — 1).
Реинвестиции по сути – направленные на развитие денежные средства (оборотные и внеоборотные активы).
3 шаг. MIRR определяется как норма дохода, при которой все ожидаемые доходы, приведенные к концу проекта, имеют текущую стоимость, равную стоимости всех требуемых затрат:
- Где:
CF+n – доходы n-го периода (положительные значения)
CF—n – затраты, (инвестиции, реинвестиции) n-го периода
WACC – средневзвешенная стоимость капитала
r – ставка дисконтирования
N – длительность проекта
Расчет MIRR актуален для случаев, когда денежные потоки нестандартные, то есть имеются как положительные, так и отрицательные потоки в период реализации проекта. Проект приемлем для инициатора, если MIRR больше эффективной барьерной ставки.
При расчете денежных потоков в MIRR положительные суммы (CF+n) относятся к притокам, а отрицательные (CF—n) – к оттокам, со сменой знака, то есть в знаменателе всегда считается модуль числа. Если стоимость оттоков превышает сумму притоков, MIRR принимает отрицательное значение, если CF—n = 0, то ставка MIRR не рассчитывается.Также, как и при расчете других показателей, в формуле используется шаг дисконтирования, указанный пользователем.
Разъяснения к формуле MIRR и рекомендации для расчетов
☛ Заметьте, для расчета показателей внутренней нормы рентабельности IRR и модифицированной внутренней нормы рентабельности MIRR используется только чистый денежный поток (Net Cash Flow, NCF). Также, на результат расчетов влияет шаг дисконтирования, выбранный пользователем.
Смысл формулы выходит из предположения равенства дисконтированных сумм финансирования проекта, а также реинвестированных средств (в данном случае – «оттоки» в чистом денежном потоке) и поступлений – положительных сумм (в данном случае – «притоки» в чистом денежном потоке).
| [1] |
Обратите внимание, для дисконтирования положительных сумм используется значение ставки MIRR (коэффициент MIRR), которую нужно найти из формулы [1]. То есть, формула MIRR [2] есть не что иное, как равноценное преобразование равенства [1].
Формула MIRR (Modified Internal Rate of Return):
| [2] |
- Где:
CF+n – доходы n-го периода (положительные значения)
CF—n – затраты, (инвестиции, реинвестиции) n-го периода
WACC – средневзвешенная стоимость капитала
r – ставка дисконтирования
N – длительность проекта
☛ Заметьте, для расчета модифицированной внутренней нормы рентабельности MIRR используется средневзвешенная ставка дисконтирования – за весь период расчета, выбранный пользователем.
Пример расчета MIRR смотрите в разделе «Особенности расчета денежных потоков в Budget-Plan Express».
Справка о программе «Budget-Plan Express», www.strategic-line.ru | Содержание справки
Поделиться:
Анализ возврата инвестиций для инвестора
Если вы ищете финансирование для своего бизнеса в виде инвестиций, вполне вероятно, что вам нужно будет включить в ваш бизнес-план оценку окупаемости инвестиций, которую инвестор может ожидать от своих вложений. Инвесторы используют расчет рентабельности инвестиций для сравнения нескольких различных инвестиций при принятии решения о том, инвестировать или нет.
Как рассчитать рентабельность инвестиций
Разные инвесторы будут использовать разные методы для расчета рентабельности инвестиций, существуют разные методы, основные из которых описаны ниже.
Представляя свой план и финансовые прогнозы по финансированию, вы должны решить, какой метод подходит для конкретной заявки, и включить рассчитанную сумму в свои документы.
Возврат инвестиций — ROI
Рентабельность инвестиций измеряет общую прибыль от инвестиций, выраженную в процентах от вложенной суммы. Он не принимает во внимание временную стоимость денег и представляет собой прибыль за весь срок действия инвестиций.
Формула возврата инвестиций:
В качестве примера, если инвестор инвестирует 100 000 в ваш бизнес и через 5 лет получает 400 000, то рентабельность инвестиций определяется как.
ROI = прибыль / инвестиции Рентабельность инвестиций = (400 000–100 000) / 100 000 = 300%
Годовая доходность инвестиций — AROI
AROI стремится давать среднегодовую доходность, основанную на общей доходности инвестиций.
AROI = ROI / Срок
Используя цифры из предыдущего примера, вычисление AROI будет выглядеть следующим образом:
AROI = ROI / Срок AROI = 300% / 5 = 60%
При расчете этого AROI подразумевается, что бизнес продолжается вечно с годовой прибылью 60 000.
Несколько
Мультипликатор сообщает инвестору, сколько раз возвращались их первоначальные инвестиции. Множитель рассчитывается по формуле:
Множественный = Общая сумма, возвращенная от инвестиции / инвестиции
В приведенном выше примере возвращенная сумма составляла 400000, а инвестированная сумма — 100000, коэффициент рассчитывается следующим образом:
Множественный = Общая сумма, возвращенная вложением / вложением Кратное = 400 000/100 000 = 4
Опять же, мультипликатор не учитывает временную стоимость денег.
Совокупный годовой темп роста —
CAGRСреднегодовой темп роста учитывает временную стоимость денег. В расчетах используются методы дисконтирования денежных потоков и делается попытка найти устойчивые ежегодные темпы роста, которым эквивалентны инвестиционные денежные потоки.
Математически совокупный годовой темп роста равен внутренней норме доходности (IRR) денежных потоков от инвестиций.
В приведенном выше примере инвестиции составили 100 000, а инвестор получил 400 000 через 5 лет.В этом простом примере внутренняя норма доходности или совокупный годовой темп роста имеет следующий вид:
Совокупный годовой темп роста = (возвращенная сумма / инвестированная сумма) (1 / срок) - 1 Совокупный годовой темп роста = (400 000/100 000) (1/5) - 1 = 31,95%
Это можно увидеть в таблице ниже
| Год | Открытие | Проценты (31.95%) | Закрытие |
|---|---|---|---|
| 1 | 100 000 | 31 951 | 131 951 |
| 2 | 131 951 | 42,159 | 174,110 |
| 3 | 174 110 | 55 630 | 229 740 |
| 4 | 229 740 | 73 404 | 303 144 |
| 5 | 303 144 | 96 857 | 400 000 |
Таким образом, когда инвестор получает 400 000 через 5 лет от первоначальных инвестиций в размере 100 000, это эквивалентно получению совокупного годового темпа роста 31.95%.
Наш калькулятор совокупных годовых темпов роста можно использовать для расчета дисконтированного денежного потока.
Типичная норма рентабельности инвестиций
В зависимости от стадии, на которой находится ваш бизнес, доход, требуемый инвесторами, будет варьироваться. Как правило, чем раньше начинается бизнес, тем более рискованным он будет восприниматься и тем выше будет требуемый доход.
Обычно инвесторы ищут наилучшую окупаемость инвестиций при совокупном ежегодном темпе роста как минимум 30-40%.В таблице ниже представлены примерные совокупные годовые темпы роста с соответствующими показателями ROI, AROI и мультипликаторами на 5-летний срок.
| CAGR | Несколько | ROI | Годовая рентабельность инвестиций |
|---|---|---|---|
| 60% | 10,5 x | 949% | 190% |
| 50% | 7,6 x | 659% | 132% |
| 40% | 5.4x | 438% | 88% |
| 30% | 3,7x | 271% | 54% |
| 25% | 3,1x | 205% | 41% |
Какой бы метод ни был выбран, прибыль, которую инвестор, как ожидается, получит от инвестиций в ваш бизнес, должна быть четко указана в резюме вашего бизнес-плана или финансовых прогнозах.
Об авторе
Дипломированный бухгалтер Майкл Браун — основатель и генеральный директор Plan Projection.Он работал бухгалтером и консультантом более 25 лет и построил финансовые модели для всех типов отраслей. Он был финансовым директором или контролером малых и средних компаний, а также руководил собственным малым бизнесом. Он был менеджером и аудитором в бухгалтерской фирме Deloitte, большой четверке, и имеет степень бакалавра наук Университета Лафборо.
Вам также может понравиться
Как внутренняя норма доходности (IRR) может ввести инвесторов в заблуждение
Внутренняя норма доходности (IRR) стала мерой для частных инвестиционных менеджеров, но эта метрика имеет серьезные ограничения, которые должны понимать все инвесторы.Настоящее богатство создается за счет накопления денег с течением времени, что отражается в метрике годовой доходности, но не в IRR. Многие инвесторы ошибочно сравнивают IRR с годовой доходностью, чтобы принять инвестиционные решения, что может быть дорогостоящей ошибкой. Инвесторам важно понимать, чем IRR отличается от годовой прибыли, чтобы принимать более разумные решения о вложении средств в недвижимость.
Годовая доходность — это сумма денег, которую инвестиции сделали или которые, как ожидается, будут приносить каждый год вложения.Например, инвестиция в 1 миллион долларов, которая дает 8% годовой доходности, будет стоить более 10 миллионов долларов через 30 лет с учетом сложного процента.
IRR, с другой стороны, пытается дать инвесторам эквивалентную годовую норму прибыли, но учитывает время движения денежных средств, даже если деньги вкладываются на короткие периоды времени, такие как дни или недели. IRR также предполагает, что все дистрибутивы будут немедленно реинвестированы, а это означает, что существует встроенное допущение сложного процента, которого на самом деле не происходит.
Благодарим вас за подписку на Origin Insights.
Обучение инвестированию в недвижимость доставляется на ваш почтовый ящик один раз в месяц.
Настоящая проблема с IRR заключается в том, что они не объясняют в измеримых долларах, сколько денег вы заработали. Например, в отличие от приведенного выше примера поддающейся количественной оценке годовой прибыли, мы не знаем, сколько сегодня стоит инвестиция в 1 миллион долларов, обеспечивающая внутреннюю норму доходности 8% за 30 лет.
Ниже приведен пример, который подчеркивает ограничения IRR при рассмотрении инвестиций в размере 100 000 долларов США за трехлетний период:
| Первоначальные инвестиции | долларов США (100 000) |
| Денежный поток в первый год | + 50 000 долларов США |
| Денежный поток во втором году | + 50 000 долларов |
| Денежный поток в третьем году | + 20 000 долларов |
| Общая прибыль от капитала | 20 000 долларов |
IRR для этой инвестиции фактически составляет 11.2% за трехлетний период. Самый простой способ рассчитать это — подключить денежные потоки к Excel и использовать функцию «= IRR». Формула просто дисконтирует денежные потоки, чтобы получить IRR инвестиции. Самым важным моментом здесь является то, что прибыль от инвестиций составила всего 20 000 долларов, или 20%. Для достижения такой же общей прибыли в годовом исчислении инвестиции должны составить 6,3%. Другими словами, если бы вы вложили 100 000 долларов в инвестицию, которая увеличивалась на 6,3% ежегодно, то через три года вложения достигли бы 120 000 долларов.Если бы 100000 долларов выросли на 11,2% в годовом исчислении, прибыль была бы ближе к 37000 долларов. Прежде чем вкладывать средства в тот фонд прямых инвестиций, который генерировал 20% годовой IRR, определите, сколько фактического богатства они создали, посмотрев на общую или множественную прибыль от инвестированного капитала.
Чтобы еще больше проиллюстрировать разницу между IRR и годовой доходностью, ниже я сравниваю две инвестиции в размере 100 000 долларов, каждая из которых генерирует 15% IRR, но дает совершенно разные прибыли.
| Сценарий № 1: | |
|---|---|
| Начальные инвестиции | (100 000 долларов) |
| Денежный поток в первый год | + 50 000 долларов |
| Денежный поток во втором году | + 50 000 долларов |
| Денежный поток в третьем году | + 28 500 долларов США |
| Общая прибыль от капитала | 28 500 долларов США |
| Сценарий 2: | |
|---|---|
| Начальные инвестиции | (100 000 долларов США) |
| Денежные средства Поток в первый год | + 0 |
| Денежный поток во втором году | + 0 |
| Денежный поток в третий год | + 152000 долларов |
| Общая прибыль от капитала | 52000 долларов |
В первом примере общий выигрыш составил 28.5%, тогда как во втором примере общий прирост составил 52%. Этот пример иллюстрирует причину, по которой сравнение двух инвестиционных возможностей друг с другом с использованием только IRR может быть дорогостоящим. Деньги обоих инвесторов были связаны на три года, но один заработал намного больше, чем другой. В сценарии № 2, приведенном выше, оказывается, что 15% IRR фактически совпадает с 15% годовой доходностью, потому что весь денежный поток происходит в конце. Инвестиции в размере 100 000 долларов США, по сути, увеличиваются из расчета 15% в год.
(статья завершается видео ниже)
Посмотрите, как Майкл Епископ объясняет, почему инвесторы не должны полагаться исключительно на IRR при оценке результатов.
Честно говоря, возврат денег раньше, чем позже, лучше и, безусловно, помогает снизить риск. Денежные потоки, которые происходят далеко в будущем, как правило, более рискованны, чем ожидаемые ранее. В сценарии № 1, приведенном выше, инвестор предположительно будет немедленно инвестировать любой полученный им денежный поток в другие инвестиции.Однако вы не знаете, какие инвестиции будут доступны в этот момент в будущем, и эти инвестиции, скорее всего, не принесут такой же IRR. Также требуется время, энергия и дисциплина, чтобы найти подходящее место для реинвестирования этих распределений.
К настоящему времени должно быть очевидно, что, хотя IRR и годовая доходность выглядят и кажутся похожими друг на друга, это очень разные показатели. Погоня за высокой IRR в короткие сроки — одна из самых больших ошибок инвесторов.Частный управляющий недвижимостью, производящий высокие IRR, может на самом деле не приносить никакого реального богатства, поэтому необходимо также посмотреть на показатель общей прибыли или мультипликатора на собственный капитал. Иногда лучше найти хорошие долгосрочные инвестиции и позволить силе компаундирования работать на вас. В долгосрочной перспективе вам может быть лучше достичь 10% годовой доходности, чем гнаться за 20% IRR. Как сказал великий Уоррен Баффет: «Остерегайтесь инвестиционной деятельности, которая вызывает аплодисменты; великие движения обычно приветствуются зевотой.”
×Ваш гид уже на пути к почтовому ящику. Пожалуйста, проверьте свою электронную почту.
Закрыть
Демистификация возврата инвестиций (ROI)
Предисловие
Почему я выбрал заголовок темы Демистифицируя рентабельность инвестиций ? Что в ней можно развенчать?
Рентабельность инвестиций — широко используемый инструмент для оценки эффективности денежных средств, потраченных на проекты исполнительным руководством.PMO или менеджеры проектов в своем качестве должны дополнять информацию или использовать концепцию ROI тем или иным образом. Концепция ROI включает сложный финансовый жаргон, такой как IRR или минимальная ставка, чистая приведенная стоимость, стоимость инвестиций, доходность и т. Д., Что довольно сложно понять нефинансовому менеджеру, поэтому финансовая терминология нуждается в разъяснении / упрощении для простоты использования. использование нефинансовых менеджеров / менеджеров проектов.
Правильное понимание концепций, задействованных в процессе ROI, менеджером проекта или PMO помогает им: Побеждать в проектах путем правильного расчета и прогнозирования ROI; Рентабельность инвестиций как инструмент предлагает огромные возможности для сравнения проектов, что улучшает финансовую видимость и принятие решений PMO.
Я взял лучшие объяснения из доступных ресурсов знаний по рентабельности инвестиций, смешал их с моим практическим опытом и изо всех сил старался представить упрощенное чтение этой статьи.
Определение термина ROI
Давайте проанализируем несколько определений.
Согласно investopedia Рентабельность инвестиций — это «показатель эффективности, используемый для оценки эффективности инвестиций».
isixsigma определяет рентабельность инвестиций как:
« ROI — это индикатор, используемый для измерения финансовой прибыли / убытка (или« стоимости ») проекта по отношению к его стоимости. Как правило, он используется для определения того, принесет ли проект положительную окупаемость. и имеют ценность для бизнеса «.
Термины, используемые в этих определениях рентабельности инвестиций, влекут за собой большую путаницу, которая объясняется / разъясняется в более поздней части этой статьи, а именно: окупаемость, период окупаемости, финансовая прибыль / убыток, эффективность инвестиций, стоимость и ценность для бизнеса.
В контексте проекта ROI — это мера, которая используется для измерения эффективности или результативности ваших инвестиций в проект. Монетизированная стоимость количественных будущих выгод рассчитывается и сравнивается с обычно ожидаемой нормой доходности, что дает вам положительный или отрицательный результат и используется для принятия решения о том, идти или не идти по проекту, это подводит итог всей рентабельности инвестиций. процесс расчета. Рентабельность инвестиций как показатель прибыли (окупаемости) по сравнению с вашими инвестициями, как правило, выражается в процентах или в виде отношения.
Формула ROI:
(возврат — стоимость инвестиций)
ROI = —————————————- X 100
Стоимость инвестиций
Где, Возврат : денежная сумма, полученная в виде увеличения дохода или экономии затрат
Стоимость инвестиций : Деньги, потраченные на проект (включая прямые / косвенные расходы, стоимость внедрения, стоимость оборудования, стоимость программного обеспечения и т. Д.)) В контексте проекта будут расходы, отдача от которых начнется по прошествии времени, поэтому важно знать, когда предприятие окупило затраты и начало приносить прибыль.
PMBOK® утверждает, что во многих проектах прогнозирование и анализ перспективных финансовых показателей продукта проектов выполняется вне проекта, но для других проектов, таких как проекты капитального строительства, расчет рентабельности инвестиций становится частью области знаний по управлению плановыми затратами в рамках группа процесса планирования, поэтому здесь признается важность ROI как инструмента.
Демистифицируете?
Да, давайте сделаем это здесь!
Поскольку концепция рентабельности инвестиций сложна и является субъективной для области применения, такой как проект ИТ-инфраструктуры, внедрение ERP, проект капитальных вложений в производство и т. Д., Необходимо уточнить и объяснить термины и методологии для простоты использования в проекте. среда управления.
Первая демистифицирующая идея касается основы расчета, т.е.Что касается финансовой выгоды / прибыли по сравнению с наличными деньгами, существует большая путаница в отношении концепции возврата, некоторые считают прибыль, которая отображается в отчете о прибылях и убытках организации, как возвращение. Но разумная практика будет заключаться в наличных деньгах, а не в прибыли, потому что расходы, понесенные по проекту, являются потраченными деньгами, поэтому их необходимо сравнивать с поступающими денежными средствами, чтобы можно было сравнить их. Harvard Business Review рекомендует рассчитывать рентабельность инвестиций на основе возможностей / наличия входящего денежного потока в качестве выгоды от продукта проекта, полученного организацией в течение ожидаемого периода реализации.
Эффективность инвестиций означает критерий, объясняющий, насколько выгоднее инвестировать в один проект по сравнению с другим (другими). Это может быть оценено как в совокупности, так и в периодическом значении ROI. Поскольку рентабельность инвестиций связывает выполнение проекта с бизнес-целями, это оказывается выгодным для руководства, позволяя избегать инвестиций в проекты, которые не достойны бизнеса.
Процесс расчета рентабельности инвестиций включает четыре основных этапа расчета рентабельности инвестиций, как было объяснено в статье Harvard Business Review Джо Найта:
Определить первоначальные капитальные затраты
Прогноз денежных средств от инвестиций
Определите минимальную прибыль, требуемую вашей компанией
Оцените свои инвестиции
Этот процесс является общим и может использоваться для расчета рентабельности инвестиций в любом контексте. Для целей данной статьи были рассмотрены конкретные расчеты и разработки проекта.
Первым шагом в определении рентабельности инвестиций является расчет капитальных затрат, которые означают, сколько денег необходимо потратить для реализации проекта. Стоимость инвестиций, или в типичной ИТ-среде, она известна как TCO (Общая стоимость владения), которая состоит из всех прямых затрат — Затраты, которые конкретно тратятся на проект путем приобретения оборудования или других ресурсов, которые будут задействованы исключительно в проекте и Косвенные затраты , которые представляют собой долю накладных расходов от общих услуг, таких как финансы и счета, общая инфраструктура, такая как телефон и Интернет и т. Д.которые специально не устанавливаются для проекта, но в проекте используются эти средства, поэтому плата является существенной для стоимости проекта. Для примера саке рассмотрим составляющие стоимости инвестиций:
| Прямые затраты: | млн. $ | Косвенные затраты: | млн. $ |
| Оборудование | Стоимость общих услуг | ||
| Серверы | $ 5.00 | Доля накладных расходов на инфраструктуру | $ 1,00 |
| Сетевые компоненты | $ 1,00 | Доля затрат на PMO | $ 0,50 |
| Прочие расходы | $ 0,50 | Доля в расходах на исполнительный надзор | $ 0,50 |
| Итого затраты на оборудование | 6 долларов.50 | Итого Общие затраты | 2,00 $ |
| Программное обеспечение | |||
| Лицензионный сбор | $ 5.00 | ||
| Разработка / настройка | $ 2,00 | ||
| Затраты на обновление / обслуживание | 0 руб.50 | ||
| Итого затраты на программное обеспечение | $ 7,50 | ||
| Менеджмент | |||
| Администратор | $ 1,00 | ||
| Хостинг и т. Д. | $ 1,00 | ||
| Итого управленческие расходы | 2,00 $ | ||
| Опора | |||
| Вспомогательный персонал | $ 1,00 | ||
| Итого вспомогательные расходы | $ 1.00 | ||
| Реализация | |||
| Разработка / настройка / интеграция | $ 5.00 | ||
| Итого затраты на реализацию | 5,00 $ | ||
| Итого прямые затраты | 22 доллара.00 | Итого косвенные затраты | 2,00 $ |
| Общая стоимость инвестиций | 24,00 | ||
* Помните, что затраты — это денежные затраты, и поэтому их необходимо сравнивать с точки зрения предполагаемых денежных вложений для расчета рентабельности инвестиций.
Второй шаг — это прогнозирование денежных средств от инвестиций, которые часто называют выгодами , это самый сложный аспект определения рентабельности инвестиций.Выгоды в совокупности составляют Деловая ценность , которая включает материальных , а также нематериальных выгод, но для целей расчета рентабельности инвестиций учитываются только материальных выгод (которые могут быть рассчитаны в виде поступающих в организацию денежных средств). Типы льгот описаны ниже:
Ощутимые выгоды — , где выгоды от проекта можно измерить в четких финансовых терминах. Это:
А.Будущая экономия затрат — сравнительные затраты на операции до и после реализации проекта, которые можно разделить на:
ИТ-персонал / услуги Экономия совокупной стоимости владения — сокращение количества случаев ошибок, количества поломок оборудования и т. Д., Которую можно напрямую количественно оценить в финансовом выражении.
Другая экономия прямых затрат
Преимущества производительности пользователей — Экономия в части оплаты труда, применяемой к количеству транзакций, обработанных до и после реализации проекта.
B. Будущие дополнительные доходы — Рост доходов по сравнению с цифрами до и после реализации проекта предлагает легко измеримые выгоды. Их можно разделить на
Рост выручки — за счет обработки большего количества заказов на продажу, это можно вычислить по количеству заказов на продажу, обработанных в AS-IS, и количеству заказов на продажу, обработанных в TO-BE
Нематериальные выгоды — это переменные, которые не могут быть количественно определены в прямой связи с проектом, но существенно способствуют получению будущих выгод, например:
Рост рыночной капитализации за счет увеличения стоимости акций
Дополнительный гудвилл / стоимость бизнеса
Удовлетворенность клиентов
Третий шаг — определение IRR (Внутренняя норма прибыли) или Hurdle Rate , это минимальная ожидаемая доходность, которую заинтересованные стороны ожидают получить от своих инвестиций.Существует множество факторов, которые влияют на IRR, такие как преобладающие на рынке процентные ставки, альтернативные издержки инвестирования в другие инструменты / проекты, стоимость капитала и риски, связанные с проектом и т. Д. Финансовый отдел или офис финансового директора не хотели бы налагать санкции на средства для любого такого проект, который приносит будущие выгоды ниже IRR. Таким образом, IRR является очень важным пороговым значением для определения ROI.
Четвертый шаг — оценить ваши инвестиции, есть 4 параметра для оценки ваших инвестиций путем расчета и анализа рентабельности инвестиций.Эти параметры: Срок окупаемости , Чистая приведенная стоимость или NPV, Срок окупаемости и Внутренняя норма прибыли или IRR.
Здесь Срок окупаемости равен стоимости инвестиций, а расчет рентабельности инвестиций определяет, как скоро окупятся инвестиции, сделанные в любой проект. Этот период восстановления известен как Срок окупаемости .Срок окупаемости данной инвестиции или проекта является важным фактором, определяющим, стоит ли браться за проект, поскольку более длительные периоды окупаемости обычно нежелательны для инвестиций. Любое подразделение, такое как месяц или год, можно рассматривать для обозначения периода окупаемости, что бы вы ни выбрали, это должно облегчить вашу внутреннюю отчетность и рассмотрение информации руководством. Внутренняя норма доходности, — это контрольный показатель, на котором сравнивается рассчитанная периодическая рентабельность инвестиций, чтобы определить, превышает ли проект ожидаемую внутренне ожидаемую доходность или нет.IRR — это периодическая ставка, которая способствует более равномерному сравнению выгоды.
Чистая приведенная стоимость — это приведенная стоимость будущих денежных выплат с учетом дисконтированной ставки для снижения влияния инфляции и уменьшения денежной стоимости выгоды.
Оценка инвестиционного процесса:
1. Некоторое руководство заинтересовано в окупаемости с точки зрения потраченных денег, простыми словами, рентабельность выгод проекта в дальнейшем рассматривается как часть прибыли / убытка от обычных операций.Временная стоимость денег / альтернативные издержки не учитываются при расчете рентабельности инвестиций с использованием метода окупаемости. Таким образом, это простой мягкий способ оценить, как скоро будут окупаться ваши затраты с даты реализации проекта, и не предлагает слишком много для облегчения принятия решений, этот метод в основном подходит для внутренних проектов модернизации и обслуживания технологий, которые не руководствуются стратегией или долгосрочным планом. Кроме того, тот факт, что инвестиции будут продолжать приносить выгоду даже после того, как период окупаемости будет проигнорирован методом окупаемости, который не дает истинной картины реальной прибыли, может быть получен проектом.
2. Некоторые компании больше озабочены окупаемостью инвестиций за весь период их владения, поэтому они должны быть заинтересованы в получении прибыли за этот период. Применяются критерии расчета чистой прибыли от достигнутой выручки, которой достаточно для возмещения окупаемости плюс минимальная ожидаемая доходность (IRR), инвестор был бы очень рад получить что-либо сверх этого
.3. Для совершенствования анализа и определения прибыли в истинном финансовом выражении важно учитывать чистую приведенную стоимость будущих денежных выгод.В инфляционной экономике деньги обесценивают свою ценность в течение определенного периода времени, предположим, что мы рассчитываем доход за 5-летний период на сегодняшнюю дату, мы должны рассмотреть вычет из этой суммы за счет инфляции, чтобы получить реальную цифру для сравнение текущей инвестиционной стоимости денег.
4. Дальнейшим шагом к расчету ROI и оценке инвестиций является сравнение доходности с IRR, руководство не заинтересовано в тратах на проекты, которые не имеют потенциальной прибыли ниже ожидаемой внутренней нормы прибыли.
Ограничения ROI:
Следует быть осторожным при оценке рентабельности инвестиций для своих проектов, поскольку она имеет определенные ограничения: во-первых, если не учитывать период окупаемости, то решение по рентабельности инвестиций может привести к ошибочным выводам. Лучший способ проанализировать рентабельность инвестиций — разделить общую рентабельность инвестиций на количество периодов, которые потребуются для получения прибыли. Это даст вам периодическую рентабельность инвестиций, которую легче сравнить с IRR. Проект с более высоким периодом рентабельности инвестиций будет предпочтительнее другого, потому что для достижения желаемой отдачи потребуется меньшее время.
Во-вторых, определенные критерии количественной оценки выгод являются субъективными в отношении ситуации и характера бизнеса, поэтому люди, участвующие в процессе расчета, должны осознавать сложность и ситуативные переменные, чтобы достичь наилучшего результата. Любой, кто отвечает за расчет рентабельности инвестиций, должен быть осторожен, чтобы не преувеличивать расчет прибыли.
Заключение:
Быстрое возмещение их инвестиций является высшим приоритетом руководства, и когда вы начинаете получать положительную отдачу, это является большим достижением.Поскольку рентабельность инвестиций является ключевым критерием выбора проекта, поэтому руководство очень внимательно за ней следит, любые негативные моменты в этом отношении могут убить будущие перспективы исполняющей организации, тогда как положительная и ранняя рентабельность инвестиций может помочь достичь наилучшего учетных данных и будущей ссылки для PMO. Команда управления проектом должна помогать руководству выделить ключевые области преимуществ, соответствующим образом соотнося это с денежными расчетами и увязывая их с бизнес-целями, определение соответствующей рентабельности инвестиций и периода окупаемости помогает проектам обеспечивать участие заинтересованных сторон, вносящих свой вклад в проект здравоохранения. организация.
Я уделил максимальное внимание тому, чтобы не усложнять весь процесс, связанный с окупаемостью инвестиций, но все же, если вы чувствуете, что тема требует доработки / разъяснения, напишите мне [email protected] Я вернусь с соответствующими разъяснениями / объяснение.
Размещено: 24 января 2017 г., 02:11 | Постоянная ссылкаМодифицированная внутренняя норма доходности, MIRR | Метод | Определение | Формула | Уравнение | Пример | Преимущества и недостатки
Юрий Смирнов к.Д.Определение
Модифицированная внутренняя норма доходности (MIRR) является модификацией внутренней нормы доходности (IRR) и используется при составлении бюджета капиталовложений в качестве критерия ранжирования для взаимоисключающих проектов. Идея метода MIRR заключается в том, что все оттоки денежных средств по проекту дисконтируются по стоимости капитала, а все поступления денежных средств реинвестируются по ставке реинвестирования.
Формула
В общих чертах уравнение MIRR можно записать следующим образом:
, где N — количество лет (периодов) инвестиций, COF t — отток денежных средств за соответствующий год (период) t, r — стоимость капитала (ставка дисконтирования), CIF — приток денежных средств для соответствующего год (период) t, k — ставка реинвестирования.
Левая часть уравнения — это приведенная стоимость всех оттоков денежных средств по проекту (знак «-» необходим, поскольку оттоки денежных средств имеют отрицательное значение). Числитель в правой части формулы — это будущая стоимость (также называемая конечной стоимостью) денежных поступлений по проекту. Таким образом, приведенное выше уравнение можно изменить, как показано ниже.
| -PV COF = | FV CIF |
| (1 + MIRR) N |
Наконец, формула модифицированной внутренней нормы доходности выглядит следующим образом:
Решение Правило
Если MIRR является единственным критерием отбора проекта, правило принятия решения довольно простое.Проект следует принять, если измененная внутренняя норма доходности превышает стоимость капитала.
Проблемы возникают при ранжировании взаимоисключающих проектов, особенно если они разного размера. В таком сценарии чистая приведенная стоимость (NPV) должна использоваться в качестве критерия ранжирования, а MIRR может использоваться в качестве дополнительного критерия, измеряющего чувствительность проекта к изменениям стоимости капитала и ставок реинвестирования.
Преимущества и недостатки метода MIRR
Модифицированная внутренняя норма доходности решает две проблемы, присущие IRR.
- Все денежные поступления реинвестируются по ставке реинвестирования, что более реалистично, чем реинвестирование по IRR.
- Метод расчета устраняет проблему множественных IRR для проектов с аномальными денежными потоками.
Основным недостатком метода MIRR является потенциальный конфликт с методом NPV. Причина может быть связана с разницей в масштабе проекта или в сроках поступления денежных потоков (проблема обсуждалась в разделе «Метод NPV vs IRR»).Более того, если ставка реинвестирования ниже стоимости капитала, возникает конфликт с основным предположением метода NPV, которое заключается в том, что все ожидаемые притоки денежных средств реинвестируются за счет стоимости капитала (ставка дисконтирования). Таким образом, проект может одновременно иметь положительную NPV и MIRR ниже стоимости капитала. По этой причине в некоторых академических исследованиях рекомендуется использовать ставку реинвестирования, равную стоимости капитала, привлеченного для проекта.
Пример
Компания N рассматривает два взаимоисключающих проекта.Стоимость капитала составляет 12%, а ожидаемая ставка реинвестирования — 10%. Подробная информация об ожидаемых денежных потоках представлена в таблице ниже.
| Первоначальная стоимость, CF 0 | Денежные потоки на конец соответствующего года, CF т | |||||
| 0 | 1 | 2 | 3 | 4 | 5 | |
| пр.У | –20 000 000 | –5 000 000 | 12 000 000 долларов США | 10 500 000 долл. США | 9 000 000 долларов США | 8 500 000 долл. США |
| пр.З | –20 000 000 | 11 000 000 долларов США | 9 000 000 долларов США | 7 500 000 долл. США | 6 000 000 долл. США | –5 000 000 |
Обратите внимание, что у проекта Z ненормальные денежные потоки, поэтому у нас есть проблема множественных IRR.
Чтобы решить приведенное выше уравнение, нам необходимо рассчитать текущую стоимость (PVCOF) всех денежных потоков и будущую (конечную) стоимость всех денежных потоков (TV) для обоих проектов.
| PV COF по проекту Y = | –20 000 000 | + | –5 000 000 | = — 24 464 285,71 долл. США |
| (1 + 0,12) 0 | (1 + 0.12) 1 |
| PV COF проекта Z = | –20 000 000 | + | –5 000 000 | = — 22 837 134,28 долл. США |
| (1 + 0,12) 0 | (1 + 0,12) 5 |
FV CIF проекта Y = 12 000 000 долларов США × (1 + 0,1) 3 + 10 500 000 долларов США × (1 + 0.1) 2 + 9 000 000 долларов США × (1 + 0,1) 1 + 8 500 000 долларов США × (1 + 0,1) 0 = 47 077 000 долларов США
FV CIF проекта Z = 11 000 000 долларов США × (1 + 0,1) 4 + 9 000 000 долларов США × (1 + 0,1) 3 + 7 500 000 долларов США × (1 + 0,1) 2 + 6 000 000 долларов США × (1 + 0,1) 1 = 43 759 100 долл. США
Схематично поступления и оттоки денежных средств по обоим проектам представлены на рисунке ниже.
Таким образом, MIRR проекта Y равен 13.99% и 13,89% для Project Z.
У обоих проектов MIRR больше, чем стоимость капитала, поэтому они могли бы быть приняты, если бы они были независимыми. Поскольку они являются взаимоисключающими, проект Y должен быть принят, а проект Z — отклонен. С другой стороны, чистая приведенная стоимость проекта Y составляет 3 118 524,40 доллара США и 3 310 499,52 доллара США для проекта Z. Таким образом, существует конфликт между NPV и методом MIRR. В таких случаях рекомендуется использовать NPV в качестве единого критерия отбора, поэтому проект Z должен быть принят.Однако следует отметить, что проект Z более чувствителен к изменению стоимости капитала и скорости реинвестирования, чем проект Y.
.MIRR в Excel
Модифицированная внутренняя норма доходности также может быть рассчитана в Excel, как показано в примере ниже.
- Выбрать выходную ячейку H7 .
- Нажмите кнопку fx , выберите категорию Все и выберите функцию MIRR из списка.
- В поле Значения выберите диапазон данных B7: G7 .
- В поле Finance_rate выберите ячейку B1 .
- В поле Reinvest_rate выберите ячейку B2 и нажмите кнопку OK .
Итак, у нас одинаковая MIRR для проекта Y, равная 13,99%, и 13,89% для проекта Z.
Возврат инвестиций (ROI) — Формула и объяснение
Рентабельность инвестиций (ROI) измеряет доходность данной инвестиции.
Рентабельность инвестиций — один из наиболее широко используемых инструментов измерения эффективности при оценке инвестиционного центра.
Инвестиционный центр — это подразделение организации, которое контролирует собственные источники доходов, понесенные затраты и используемые активы (инвестиции). Инвестиционный центр действует как отдельная компания.
Формула возврата инвестиций (ROI)
Основная формула расчета рентабельности инвестиций:
| ROI | = | Доход |
| Инвестиции |
Доход может быть одним из следующих: операционная прибыль или EBIT (прибыль до уплаты процентов и налогов), чистая прибыль или чистый приток денежных средств.
Инвестиции могут быть: общие активы, оборотный капитал, акционерный капитал или первоначальные денежные затраты. Если возможно, используется средняя сумма за период.
Примеры: расчет ROI
1. Рассчитайте рентабельность инвестиций (ROI) инвестиционного центра, который имел операционную прибыль в размере 500 000 долларов США и операционные активы в размере 2 500 000 долларов США.
| ROI | = | Операционная прибыль |
| Итого активы | ||
| = | 500 000 долл. США | |
| 2 500 000 долл. США | ||
| Рентабельность инвестиций | = | 20% |
2.Вычислите рентабельность инвестиций (ROI) подразделения, операционная прибыль которого составила 240 000 долларов США. Его общие активы составляли 1 500 000 долларов на начало периода и 2 500 000 долларов на конец.
| ROI | = | Операционная прибыль |
| Средняя сумма активов | ||
| = | $ 240 000 | |
| (1 500 000 долл. США + 2 500 000 долл. США) ÷ 2 | ||
| Рентабельность инвестиций | = | 12% |
Анализ рентабельности инвестиций
Чем выше окупаемость инвестиций, тем лучше.Руководство может использовать контрольные показатели при оценке рентабельности инвестиций. Например, скажем, в конкретной отрасли средний ROI составляет 20%. Если ROI субъединицы составляет 8%, то это даже не половина приемлемого показателя. Руководство может решить, как повысить рентабельность инвестиций подразделения или отказаться от него и инвестировать в более прибыльные предприятия.
Кроме того, при оценке инвестиций окупаемость инвестиций должна превышать стоимость капитала , чтобы считаться прибыльной.
Подробная разработка и анализ проекта
Подробная формулировка и анализ проектаФинансовый анализ применяется в основном к проектам, предназначенным для приносить доход.Возможен анализ социальных проектов, экологических предприятий или деятельности по поддержке производства путем расчета и присвоения искусственные цены, но такой «экономический анализ», как правило, слишком комплекс для малых и средних предприятий проекты [13] .
Для доходоприносящих проектов рентабельность активность — первый и самый важный фактор, определяющий устойчивость, потому что ни один коммерческий проект не выживет, который не генерирует достаточный доход, чтобы покрыть операционные расходы и оплатить финансовые затраты.Однако, Существует несколько способов определения прибыльности инвестиций. Каждый подход имеет свои сильные и слабые стороны. Поэтому удобно использовать более одного метода.
Также важно понимать, что полученные цифры через финансовый анализ не очень полезны сами по себе; они должны быть интерпретируется. Это ответственность специалиста, выполняющего процесс формулирования и оценки проекта для объяснения заявителям, а также комитету, рассматривающему заявку на финансирование, значимость результатов, а также сочетание доходности расчеты с другими показателями вероятного успеха и устойчивости, такими как возможности и приверженность соискателей, надежность рынка, сложность технологии, влияние на окружающую среду и степень организация управления.
A. Измерения Осуществимость инвестиций
После определения всех затрат и доходов для период анализа (будь то 8, 12 или 20 лет), следующие вопросы должны быть спросили: Какие измерения будут использованы для определения осуществимости инвестиции в финансовом отношении? Как мы можем интерпретировать эти результаты?
В RuralInvest используются два разных измерения. модели для этой цели, каждая из которых имеет свои достоинства и недостатки.Все вместе они дают исчерпывающее видение предлагаемого проекта осуществимость.
1. Годовой денежный поток
Годовой денежный поток в значительной степени позволяет избежать проблемы сравнения затраты в один год с выгодами в другой год путем оценки затрат и доходов каждый год, используя только денежных затрат и доходов. Стоимость вложения входит в этот анализ через выплату кредита, взятого на финансирование Это.
Годовой денежный поток рассчитывается путем сложения всех денежных доходов из каждого года и за вычетом всех денежных затрат за тот же год; результат чистый годовой доход.Затем вычтите стоимость финансирования (капитал и интерес) от этого результата. Если оставшаяся сумма все еще положительна, то проект будет приносить достаточный доход в течение этого года для покрытия всего производства расходы, а также расходы по кредиту, и все равно оставлять некоторую сумму прибыли (оставшееся количество).
Годовой денежный поток представляет наибольший интерес для потенциального кредитора (банк, проект, кооператив и т. д.), поскольку он показывает, проект сможет генерировать достаточно денежных средств, чтобы оплатить все затраты и при этом удовлетворить затраты на финансирование.Также, как правило, это мера, которую легче всего понять. сами заявители, хотя должны понимать, что, беря только наличные, такой подход может упустить из виду важные затраты и выгоды, которых нет в деньгах термины.
2. Финансовая прибыльность
Измерение денежного потока представляет собой только снимок денежная позиция каждый год; он не предлагает общей оценки проекта. Поэтому это не очень полезно для сравнения разных проектов или для оценка проекта относительно некоторого эталона.Если правительство, девелоперский проект или даже сам заявитель желает выбрать наиболее продуктивно использовать имеющиеся средства, им понадобится другое измерение Это требует оценки финансовой рентабельности проэкт.
Финансовый анализ берет результаты за все годы исследуемых и представляет их в виде единого рисунка. Однако для достижения Для достижения этой цели методология должна учитывать уменьшение стоимости денег и общие преимущества, возникающие с течением времени.Как должен этот анализ проводить?
Мы будем использовать в качестве примера следующее: Если бы человек был предложили возможность инвестировать в проект стоимостью 1000 долларов США. сегодня, но который приносит доход в размере 2000 долларов США завтра, мало кто будет колебаться (при условии веры в честность руководителей проекта). Однако, если вместо этого предложение представляет собой инвестицию в размере 1000 долларов США, чтобы заработать 1001 доллар США за 5 лет, не было бы берущих. Следовательно, вопрос состоит в том, чтобы решить: какая скорость окупится ли инвестирование в проект? Другими словами, что норма прибыли представляет собой выгодное вложение и хорошее использование имеющихся Ресурсы?
Есть два основных измерения, которые пытаются реагировать на этот вопрос: чистая приведенная стоимость (NPV) и внутренняя норма доходности (IRR).И то и другое имеют несколько общих ключевых элементов:
Они заряжают общая стоимость инвестиции в год, в котором она имеет место, так что метод финансирования и стоимость не влияют на результат анализа. Помнить, цель анализа — определить хороший проект, а не выбрать лучший вариант финансирования .
Они оба включают стоимость основные активы проекта на конец периода анализа (например, здания, машины и другие существенные предметы).Это, конечно, не наличными, поэтому исключаются из годового анализа денежных потоков, но имеют ценность и не следует забывать.
Они оба оценивают самообеспечение (например, неоплачиваемый семейный труд) и самопотребление (использованная продукция или потреблены, но не оплачены наличными).
Они регулируют значение будущие выгоды таким образом, что 1 доллар США сегодня стоит больше, чем 1 доллар США за один год, что, в свою очередь, будет стоить более 1 доллара США через два года и т. д.Этот процесс называется , дисконтируя будущие выгоды по сравнению с преимущества сегодня.
a) Чистая приведенная стоимость
Простейшим измерением является чистая приведенная стоимость (NPV). После расчет чистой годовой прибыли за каждый год (как в годовом денежном потоке, но с указанными выше различиями) применяется ставка дисконтирования для уменьшения стоимость как чистой прибыли, так и убытков в будущие годы. Помните, что скидка ставка противоположна процентной ставке.Если у меня есть 1 доллар, процентная ставка 10% даст мне 1,10 доллара в год. Точно так же ставка дисконтирования 10% будет означает, что 1,10 доллара, полученные через год, сегодня стоят всего 1 доллар (его настоящее значение). Итак, NPV — это цифра, которая представляет ценность проекта после дисконтирование чистых будущих выгод.
Если, например, я требую процентную ставку 8% на свои деньги, тогда применение ставки дисконтирования 8% к будущим чистым выгодам от проекта обеспечит что я получу эту отдачу.Если оставшаяся сумма (ЧПС) равна 0, проект генерируя ровно 8% необходимых. Если NPV положительный, я получил свой требуемая ставка (8%) и получите эту сумму в качестве бонуса. Когда NPV отрицательный, это означает, что вложение не может принести ожидаемые 8%; это должно было бы заработать (после дисконтирования) дополнительная сумма, эквивалентная сумме NPV для достижения точка безубыточности.
Например, представим, что проект, в котором инвестиции в размере 250 долларов дают шесть лет выгоды в размере 50 долларов в год, или в общей сложности 300 долларов США (см. предыдущую страницу).Казалось бы, есть прибыль 50 долларов. Но это верно только в том случае, если вы не принимаете во внимание временную стоимость денег. Если вместо этого вы применяете ставку дисконтирования 8%, и вы видите, что на самом деле проект не очень привлекательно. Чистая приведенная стоимость инвестиций в 250 долларов составляет -0,34 доллара. То есть скажем, если вам требуется инвестиция для получения процентной ставки 8%, она не соответствует эта цель на сумму 0,34 доллара США.
Очевидно, что критическим аспектом расчета NPV является выбор учетной ставки (или процентной ставки).Высокая ставка приведет к отказ от большего количества проектов и будет отдавать предпочтение тем проектам, которые генерируют свои заработки в первые годы. Низкая ставка дисконтирования обычно приводит к принятие большего количества проектов и большее значение полученной выгоды в более отдаленном будущем.
Но как выбрать ставку дисконтирования? Самый правильный определение, как указано Всемирным банком, заключается в том, что это ставка, равная увеличение валового внутреннего продукта (ВВП) в результате инвестирования один дополнительный доллар в данной стране.Итак, если доллар вызывает увеличение 1,07 доллара США в ВВП страны, в которой вы живете, ставка дисконтирования должна быть 7% — потому что тогда ваши вложения будут равны или лучше среднего для экономики в целом. Однако такое определение легче сказать, чем измеряется, потому что нет простого способа сделать необходимые расчет.
Для практических целей лучше сказать, что скидка ставка — требуемая годовая чистая прибыль (без инфляции) чтобы вложение стоило затраченных усилий.Однако эта ставка не останется одинаково для всех инвесторов или всех инвестиций. Это будет во многом зависеть от альтернативы, которые доступны, и, даже больше, о рисках, которые проект лица. Инвестору крупного солидного банка, вероятно, потребуется меньшая скидка. ставка на будущие доходы, чем те, кто вкладывает деньги в разведку месторождений нефти компания, где вознаграждение может быть высоким, но банкротство всегда возможность.
Во многих случаях принято использовать 8%, но любые цифра от 6% до 12% будет приемлемой.Однако помните, что инвестиции с высоким уровнем риска требуют более высокой нормы прибыли, и если можно найти несколько других вариантов использования имеющихся средств, это может быть приемлемо чтобы снизить ставку.
б) Внутренняя норма прибыли
Внутренняя норма прибыли (IRR) [14] использует методологию, очень похожую на что NPV. Ключевое отличие состоит в том, что при использовании IRR спрашивают какую учетную ставку (или процентную ставку) поддержат эти инвестиции? Если IRR составляет 15%, это означает, что первоначальные инвестиции принесут процентную ставку в размере 15% в течение срока действия проекта.
Вычислить IRR сложно, так как сначала нужно догадаться о IRR, затем запустите расчет NPV и посмотрите, положительна ли полученная NPV или отрицательный. Затем расчетная IRR корректируется (вверх, если NPV положительный, вниз, если он отрицательный), и расчет повторяется снова. Это продолжается до тех пор, пока NPV достигает ровно нуля. Это IRR.
Когда-то эти вычисления были очень утомительной процедурой, но в наши дни компьютер упростил задачу, сделав за секунду то, что аналитик несколько лет назад на это могло уйти много минут.
B. Влияние налогов
В методологии RuralInvest мало внимания уделяется расчет налогов, особенно связанных с доходами. Хотя эти налоги могут оказаться важными в хорошо зарекомендовавших себя и успешных проектах (для например, в случае агропромышленного предприятия) они не имеют отношения к определение целесообразности небольших вложений. Проблема в том, что эти с которыми сталкиваются проекты — это скорее вопрос выживания, чем оценка налогов на заработок.
При работе с другими видами налогов (например, имущественные налогов) методология RuralInvest рассматривает их просто как другие косвенные или общие затраты, и они должны быть включены в таблицы для этих расходы.
C. Подготовка Рекомендации
Слепая вера в результаты финансового анализа, как руководство по утверждению инвестиционного предложения, опасно для следующих причины:
а) Компьютер может обрабатывать только те данные, которые питается в нем.Следовательно, качество расчета, генерируемого форматами в значительной степени зависит от качества информации, предоставляемой заявители и их технические специалисты. В реальном мире очень мало информация достоверна на 100%. Оценка цен, затрат, объемов и продолжительности может ошибаться, несмотря на все усилия вовлеченных лиц. Так что, это важно помнить, что финансовый анализ представляет результаты исходя из предположений, сделанных теми, кто поставил информация .
б) Проект, который приносит прибыль, может быть успешным, но находится в нет возможности гарантировать успех. Даже если цифры, использованные для расчета надежны, проект все равно может провалиться. Среди других факторов возникающие проблемы от плохо преданных участников, неэффективного управления или неожиданного изменение цен может разрушить прибыльный проект. Поэтому очень важно, чтобы вы учитывать все факторы, которые могут повлиять на успех инвестиций, и не только финансовая рентабельность.
Как можно распознать и учесть эти риски в представляете результаты оценки? Во-первых, очень важно воспользоваться о значительной скорости и мощности компьютера. Как только данные были вошел, очень легко проверить альтернативные возможности без необходимости повторить всю предыдущую работу. Сразу видно влияние изменения, иногда путем изменения одного числа. Это называется «анализ чувствительности» и его цель — показать, как результаты исследования изменятся с небольшими изменения в сделанном предположении.
Например, если средняя цена товара составляет 10 долларов, какое произойдет если цена упадет всего до 8 $ Если прибыль полностью исчезнет (или даже становится убыточным), вы знаете, что рентабельность вложения очень сильно зависит от цены товара или услуги, которую он производит и продает. Эту же процедуру можно использовать и для некоммерческого проекта. Как бы эксплуатационные расходы общественной поликлиники пострадают, если количество пациентов посещаемость была ниже, чем ожидалось? Если сообщество полагается на стандарт субсидия на пациента от Министерства здравоохранения, тогда ниже, чем ожидалось количество пациентов может означать, что клиника не может покрыть свои накладные расходы (медсестра, освещение, ремонт и др.) и должен быть закрыт.
Для проведения анализа чувствительности техник должен:
a) Определите эти элементы проекта для который: (i) существуют сомнения относительно правильного числа для использования (например, если цена быть 6, 8 или 10), и (ii) которые, как ожидается, будут важны для проекта (могут возникнуть сомнения в цене на скрепки, но, вероятно, не будет стоит проверить влияние этого изменения на производительность проекта). Обычно такие элементы включают в себя: цены на продукцию, количество предполагаемых пользователей, стоимость входы; объемы производства, эффективность производственного процесса (т.е. как требуется много вложений для производства 1 кг. мощности), время, необходимое для запуска или урожайность (в случае, например, древесных культур) и когда производство уже начато, время, необходимое для выхода на полный уровень производства.
б) Определите вероятный диапазон возможностей для каждого фактора. Например, для анализа цен можно сказать, что, хотя средний цена 10 долларов, возможный диапазон от 7 до 12 долларов.
c) Вставить новые цифры в компьютерные таблицы RuralInvest и обратите внимание на результаты.Лучший способ представить результаты — это организовать цифры в диаграмму, демонстрирующую рентабельность инвестиций для каждого фактор (цена, стоимость и т. д.) со средними, пессимистическими и оптимистическими предположениями, но это не существенно.
d) В сопроводительном письме, которое должно сопровождать подробный анализа, аналитик должен определить те факторы, для которых проект наиболее чувствительны и указывают, как вариации этих факторов могут изменить рентабельность вложения, например:
«Хотя предложение об установке системы полива выглядит довольно выгодно, следует отметить, что он очень чувствителен к колебаниям урожайность выращенных овощей.Если вместо 12 метрических тонн на гектар (т / га), получается всего 10 т / га, проект становится маржинальным. Если доходность снижается до 9 мт / га или менее, инвестиции перестают быть выгодно ».
e) Когда предложение показывает высокую чувствительность к изменениям ключа факторов, отчет технического специалиста должен учитывать вероятность этих встречающиеся вариации, например:
«Однако заявители имеют большой опыт выращивания овощи и уже получают урожай выше 12 т / га в нескольких районах где теперь летом есть доступ к воде.Риск ниже чем поэтому ожидаемая урожайность не считается очень высокой ».
Шаги, описанные выше, гарантируют, что люди, рассматривающие в предложениях по финансированию содержится информация, необходимая для информированного решение.
Что касается относительной важности финансовых и других факторов успеха проекта, ответственность за это несет технический специалист формулировки и оценки, чтобы внимательно рассмотреть и определить любые другие аспект предложения, который может повлиять на его осуществимость, а не полагаться исключительно на финансовом анализе.В сопроводительном письме предложения следует указать на способность кандидатов управлять и администрировать инвестиций для устойчивости проекта с точки зрения окружающей среды влияние и использование ресурсов и риски, которые могут встреча.
Помните, вы никому не делаете одолжение, рекомендуя инвестиции, которые не имеют хороших шансов на успех. Где проект финансируется за счет кредита, неудача может оставить группу или сообщество в долгу, с нет возможности погасить его (вероятно, ограничивая доступ к финансированию в будущее).Даже в случае проекта, который использует только пожертвованные средства, вы должен помнить, что каждая неудача означает, что был еще один хороший проект, который не смог получить ресурсы, необходимые для успеха.
Инвестирование в существующую деятельность — важность Дополнительные затраты и доходы Процедуры, описанные в этой главе, в основном предполагают, что предлагаемые инвестиции совершенно новые, поэтому все расходы и доходы будут напрямую связано с проектом.Это, безусловно, самый простой случай. Но что, если инвестиции применяются к более ранней существующей деятельности, где уже есть затраты и доходы? Как может быть влияние новых инвестиций? правильно отражены в финансовом анализе? Ответ таков, где предлагаемые инвестиции приведут к изменениям в существующей деятельности, это необходимо изучить затраты и выручку как с новым, так и без него. проект . Возьмем, например, случай группы, которая в настоящее время дыни на поле 3 га.Они хотят установить насос для подачи воды. из ближайшего ручья в сухой сезон для дополнительного орошения. Очевидно, что затраты на покупку и эксплуатацию насоса — это новые затраты, но какие? о реальном производстве? Чем больше воды доступно, возможно, стоит добавляя больше удобрений и других питательных веществ, чтобы дыни могли полное использование новой поставки. В настоящее время группа применяет 2,5 мешка удобрений на гектар, но группа решает увеличить это количество до 3.5 пакетов, если есть вода. Таким образом, дополнительное использование удобрений составит 1 мешок / га, и дополнительная стоимость будет равна цене 3 дополнительных мешков (на 3 га). В настоящее время урожайность составляет 5 т / га, но группа уверена, что это можно увеличить до 8 т / га при орошении. Таким образом, дополнительный доход составляет 3 тонн на гектар, или 9 тонн в целом, умноженное на цену за тонну, полученную за дыни. Другие дополнительные затраты, понесенные новым проектом, могут возникнуть в результате изменения количества посеянных семян, увеличение количества дынь, подлежащих собранный урожай, а также увеличенное количество мешков или ящиков, необходимых для упаковка. Помните, если вы примените все затраты и доходы, ожидаемые после новых инвестиций, вы можете дать неправильный ответ на рентабельность дополнительных вложений. В приведенном выше случае важно для сравнения только дополнительных затрат (насос, внесение удобрений и т. д.) с дополнительным выпуском 9 тонн дынь. Если топливо для насоса дорого, или если прогнозируемое увеличение урожайности невелико, это не невозможно что группе было бы лучше без полива, но они не могут знать если они не используют дополнительных затрат и доходов . |
Об авторе