Районный коэффициент к заработной плате: Районный коэффициент и северная надбавка 2022: как рассчитать, пример расчета

Содержание

Департамент общего аудита о районном коэффициенте к заработной плате в г. Новосибирск

Ответ

В соответствии со статьей 316 ТК РФ размер районного коэффициента и порядок его применения для расчета заработной платы работников организаций, расположенных в районах Крайнего Севера и приравненных к ним местностях, устанавливаются Правительством Российской Федерации.

Органы государственной власти субъектов Российской Федерации и органы местного самоуправления вправе за счет средств соответственно бюджетов субъектов Российской Федерации и бюджетов муниципальных образований устанавливать более высокие размеры районных коэффициентов для учреждений, финансируемых соответственно из средств бюджетов субъектов Российской Федерации и муниципальных бюджетов. Нормативным правовым актом субъекта Российской Федерации может быть установлен предельный размер повышения районного коэффициента, устанавливаемого входящими в состав субъекта Российской Федерации муниципальными образованиями.

Анализ статьи 316 ТК РФ во взаимосвязи со статьей 315 ТК РФ позволяет сделать вывод, что положения статьи 316 ТК РФ относятся только к районным коэффициентам, предусмотренным для сотрудников организаций, расположенных в районах Крайнего Севера и приравненных к ним областях.

В настоящее время перечень районов Крайнего Севера и приравненных к ним местностей установлен Постановлением Совета Министров СССР от 10.11.67 № 1029.

Новосибирская область в данном перечне отсутствует.

Не распространяется на Новосибирскую область и Закон РФ «О государственных гарантиях и компенсациях для лиц, работающих и проживающих в районах Крайнего Севера и приравненных к ним местностях» от 19.02.93 № 4520-1, поскольку в отношении Новосибирской области установлен только районный коэффициент и не установлена надбавка к заработной плате[1].

В соответствии со статьей 146 ТК РФ оплата труда работников, занятых на тяжелых работах, работах с вредными, опасными и иными особыми условиями труда, производится в повышенном размере.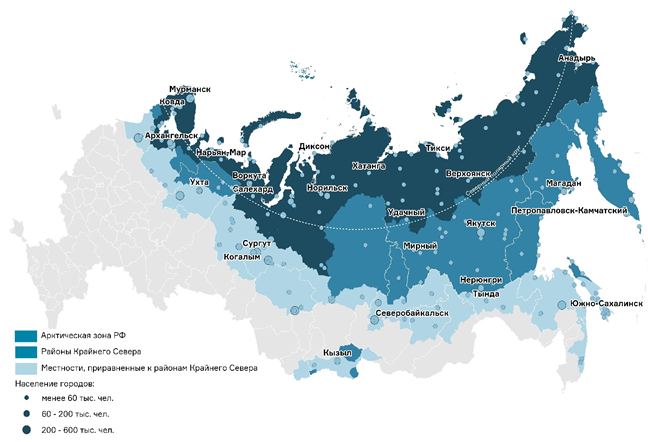

В повышенном размере оплачивается также труд работников, занятых на работах в местностях с особыми климатическими условиями.

Оплата труда на работах в местностях с особыми климатическими условиями производится в порядке и размерах не ниже установленных трудовым законодательством и иными нормативными правовыми актами, содержащими нормы трудового права (статья 148 ТК РФ).

В настоящее время, как справедливо указано в Вашем вопросе, действует Постановление Правительства РФ от 31.05.95 № 534, пунктом 17 которого установлен районный коэффициент 1,2.

При этом на период стабилизации социально-экономической ситуации в области предоставить администрации Новосибирской области право увеличивать в отдельных административных образованиях выплаты по районному коэффициенту

на 50 процентов с учетом уровня жизни населения (пункт 17 Постановления № 534).

Во исполнение данного положения Администрацией Новосибирской области в Постановлении от 20. 11.95 № 474[2] был установлен коэффициент 1,25.

До настоящего времени данное Постановление № 474 не отменено. Право на установление повышенного коэффициента было дано Администрации Новосибирской области Постановлением Правительства РФ, и в указанном Постановлении № 534 отсутствуют положения о том, что повышенный коэффициент будет распространяться только на организации, финансируемые из областного бюджета.

Таким образом, применение Постановления Администрации Новосибирской области продиктовано полномочиями, данными Администрации Новосибирской законодательным актом федерального уровня.

Как указано в Постановлении № 534, данные полномочия Администрации Новосибирской области предоставлены на период стабилизации социально-экономического положения.

Следует отметить, что в Постановлении Губернатора Новосибирской области от 03.12.07 № 474[3], в частности, указано:

«В настоящее время Новосибирская область столкнулась с необходимостью переломить отмеченные негативные тенденции, существенно усилить и стабилизировать позитивную динамику экономического роста, достигнутую в последние годы, и вернуть себе статус одного из наиболее динамично развивающихся и прогрессивных регионов России, отвечающего вызовам XXI в. »

Таким образом, как следует из данного документа, несмотря на положительный экономический рост, стабилизация социально-экономического развития региона в настоящее время еще не достигнута. Соответственно, формально

основания для неприменения районного коэффициента 1,25, по нашему мнению, отсутствуют.

Вместе с тем, как справедливо отмечено в Вашем вопросе, в районах Крайнего Севера и приравненных к ним областях районные коэффициенты, установленные субъектами РФ, применяются только к бюджетным учреждениям. При этом в Новосибирской области, не подпадающей под регулирование статьи 316 ТК РФ, повышенный коэффициент распространяется на все организации, что по нашему мнению, свидетельствует об отсутствии единообразия в применении норм действующего законодательства в отношении районных коэффициентов. В целях разрешения данного вопроса рекомендуем Вам обратиться за письменными разъяснениями в Минтрудсоцразвития РФ.

[1] В соответствии с пунктом 3 Постановления ВС РФ от 19.

02.93 № 4521-1 «О порядке введения в действие Закона РФ «О государственных гарантиях и компенсациях для лиц, работающих и проживающих в районах Крайнего Севера и приравненных к ним местностях» государственные гарантии и компенсации, предусмотренные указанным Законом, распространяются на районы Севера, в которых начисляются районный коэффициент и процентная надбавка к заработной плате, но не отнесенные к районам Крайнего Севера и приравненным к ним местностям.

[2] «О введении повышенного районного коэффициента к заработной плате на территории области»

[3] О стратегии социально-экономического развития Новосибирской области на период до 2025 года

Ответы на самые интересные вопросы на нашем телеграм-канале knk_audit

Назад в раздел

Применяют ли районный коэффициент к единовременной премии

Применяют ли районный коэффициент к единовременной премии — БУХ.1С, сайт в помощь бухгалтеру

Новости для бухгалтера, бухучет, налогообложение, отчетность, ФСБУ, прослеживаемость и маркировка, 1С:Бухгалтерия

Новости
Статьи
Вопросы и ответы
Видео
Форум

02. 11.2022

Роструд разъяснил, нужно ли применять районный коэффициент к единовременной премии за достижение высоких объемов продаж, если она выплачивается на постоянной основе и не предусмотрена в трудовом договоре.

В своем письме от 27.09.2022 № ПГ/23987-6-1 ведомство отмечает, что в соответствие со статьей 315 ТК РФ оплата труда в районах Крайнего Севера и приравненных к ним местностях должна осуществляться с применением районных коэффициентов и процентных надбавок к заработной плате. При этом районные коэффициенты и процентные надбавки начисляются на заработную плату в целом, а не на отдельные ее составляющие.

Согласно позиции Минтруда, районные коэффициенты и процентные надбавки начисляются на фактический месячный заработок работника, в который включаются в том числе премии и вознаграждения, предусмотренные системами оплаты труда или положениями о премировании организации, и другие выплаты, установленные системой оплаты труда организации.

Соответственно, районные коэффициенты и процентные надбавки начисляются на заработную плату в целом, включая в том числе предусмотренное системой оплаты труда вознаграждение, выплачиваемое единовременно.

Следить за новостями удобно в нашем новостном Telegram-канале. Присоединяйтесь!

Темы: районный коэффициент, северные надбавки, премирование, выплаты работникам

Рубрика: Зарплата при различных системах оплаты труда , Компенсации, надбавки, доплаты

Подписаться на комментарии

Отправить на почту

Печать

Написать комментарий

В 2024 году МРОТ будет повышен на 18,5% Вправе ли работодатель требовать возмещения расходов на спецодежду при увольнении Минфин напомнил правила учета компенсации за использование работником личного автомобиля В Госдуму внесли закон о МРОТ на 2024 год Когда работодатели должны сдавать сведения о просроченной зарплате в 2023 году

Опросы

Изменение правил сдачи статистической отчетности для малого бизнеса

Нужно ли изменять правила сдачи статистической отчетности для малого бизнеса?

Да, я думаю, что правила сдачи отчетности в Росстат следует упростить.

Нет, я против каких-либо изменений.

Думаю, малый бизнес нужно полностью освободить от статистической отчетности.

Мероприятия

1 февраля – 15 мая 2023 года — Конкурс корпоративной автоматизации «1С:Проект года»

5 апреля 2023 года — ЕДИНЫЙ ОНЛАЙН-СЕМИНАР 1С для бухгалтеров и руководителей

1C:Лекторий: 28 марта 2023 года (вторник) — Маркировка пива и слабоалкогольных напитков в программах «1С:Предприятие»

1C:Лекторий: 30 марта 2023 года (четверг, начало в 12:00) — Контролируемые сделки в программах «1С:ERP» и «1С:КА»

Все мероприятия

Статистические данные 101 для равенства в оплате труда

Вы приступили к изучению равенства в оплате труда, но не помните, что доктор Скретчанснифф сказал на вашем занятии по статистике 101? Поскольку статистический анализ становится все более распространенным в нашей повседневной жизни HR, мы составили список наиболее распространенных терминов в базовой статистике и регрессионном анализе. Здесь вы узнаете, что означает каждый термин, и увидите несколько практических примеров, использующих исследования равенства в оплате труда в качестве руководства.

Хотя это руководство должно быть полезным в отношении равенства в оплате труда, концепции носят более универсальный характер, и мы полагаемся на примеры в сфере оплаты труда и за ее пределами. Руководство разделено на пять разделов, направленных на пять основных основ анализа, которые мы видим в этих исследованиях равенства в оплате труда.

1.   Показатели центральной тенденции
2    Статистика распределения
3.   Статистический вывод и проверка гипотез
4.   Регрессионный анализ и переменные
5.   Вывод регрессии

понимать середину данных и делать наилучшие предположения о том, что мы можем наблюдать в наших данных или за их пределами.

Среднее

Одним из основных понятий в статистике является среднее значение. Это просто математическое среднее, которое представляет собой сумму наблюдений или чисел, деленную на количество наблюдений.

Возьмите компанию ABC, которая занимается продажей автомобилей. Руководство хочет анализировать эффективность продаж с течением времени. В таблице ниже показаны средние продажи компании ABC в год за каждый из последних пяти лет.

Среднее значение равно 540 000 (сумма проданных единиц, деленная на 5). Он придает одинаковый вес верхним значениям, поэтому, если 2021 год был особенно плохим для ABC из-за нехватки микросхем, это значительно снизит среднее значение.

В стандартном исследовании равенства в оплате труда мы обычно рассчитываем среднее значение заработной платы для женщин и мужчин, а также для расовых меньшинств и лиц, не принадлежащих к меньшинствам, для сравнения. Помните, что это всего лишь стандартная средняя заработная плата без учета какой-либо переменной, определяющей заработок. По этой причине, когда мы их сравниваем, мы часто называем анализ необработанным или неконтролируемым разрывом в оплате труда.

Медиана

Медиана — это просто среднее значение в списке чисел.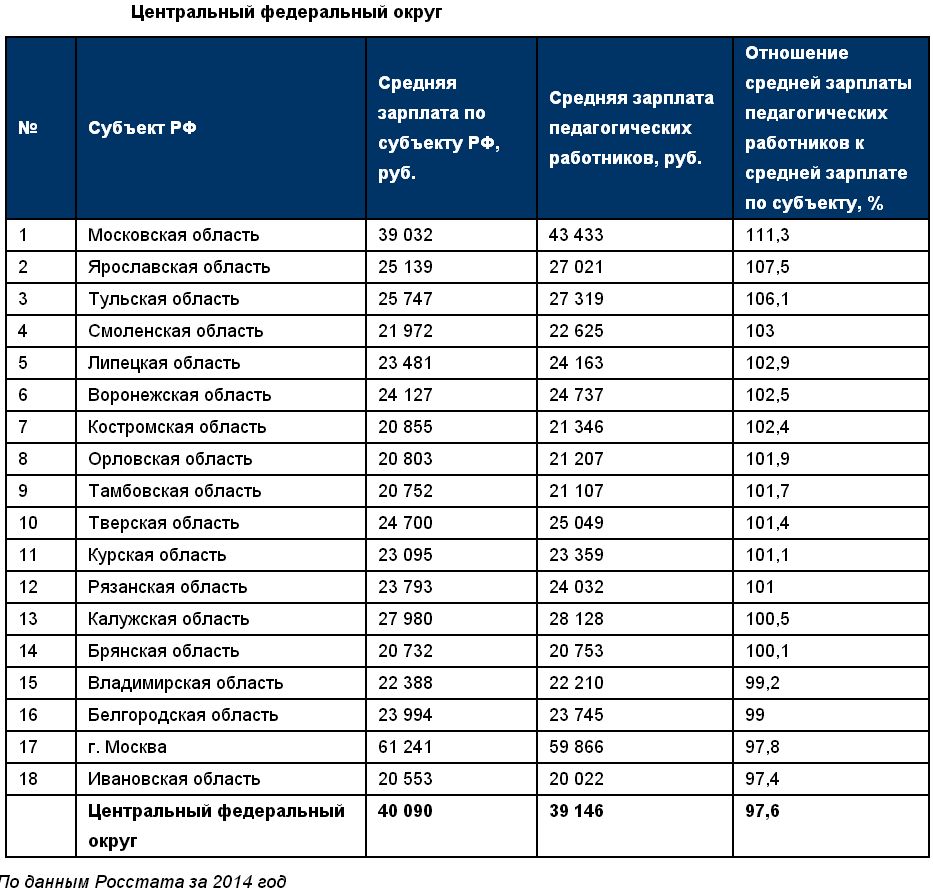 Предположим, что компания ABC также хочет получить данные о своих медианных продажах за пятилетний период. Чтобы выяснить это, нам нужно сначала отсортировать список, упорядочив проданные единицы от наименьшего к наибольшему.

Как видно из таблицы, медианное (или среднее) значение составляет 500 000 единиц, что было достигнуто в первый год. Обратите внимание, что, в отличие от среднего, особенно хороший или плохой год практически не влияет на медиану.

При стандартном анализе равенства в оплате труда мы также рассматриваем медианную заработную плату женщин и медианную заработную плату мужчин, а также медианную заработную плату представителей расового меньшинства и медианную заработную плату лиц, не принадлежащих к меньшинствам. Поскольку среднее (или среднее) иногда может быть смещено из-за оплаты нескольких сотрудников на обоих концах спектра, медиана может быть дополнительным способом измерения справедливости в оплате труда.

2. Статистика распределения

В начало

В то время как среднее значение и медиана описывают середину набора данных, статистика распределения позволяет понять, как выглядят данные в целом.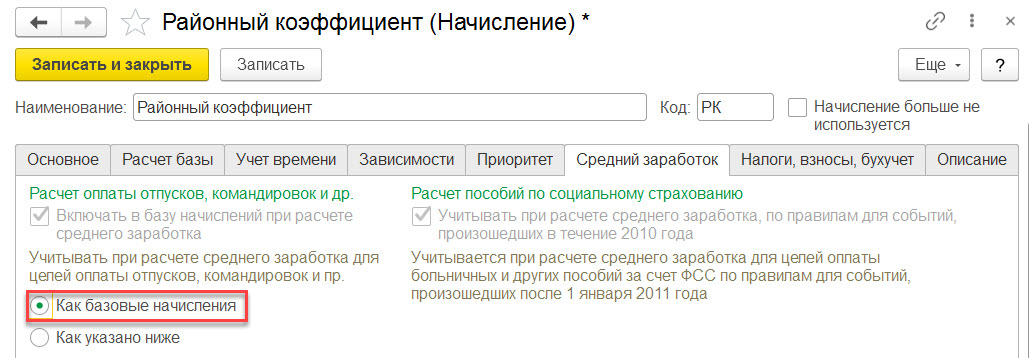

Стандартное отклонение

В статистике стандартное отклонение относится к степени вариации или дисперсии набора чисел вокруг среднего значения. Другими словами, это расстояние от среднего. Стандартное отклонение обозначается греческой буквой сигма (σ) и рассчитывается на основе расстояния каждой точки данных от среднего значения.

Если мы посчитаем стандартное отклонение продаж автомобилей для компании ABC, оно составит 120 675. Простое эмпирическое правило заключается в том, что около 95% типичного набора данных находятся в пределах двух стандартных отклонений от среднего.[1] Другими словами, если бы стандартное отклонение было равно 1000, мы ожидали бы увидеть очень небольшое изменение из года в год или мы ожидали бы увидеть наблюдения, сгруппированные вокруг среднего значения. Если бы это было 50 000, это означает, что наблюдения разбросаны от среднего значения, и мы бы приняли большие изменения как вполне разумные.

Кривая PDF

Функция распределения вероятностей, или кривая PDF, представляет собой графическое представление распределения вероятностей наблюдений. Короче говоря, площадь под кривой отражает вероятность того, что наблюдение находится в этом диапазоне. Более высокие области отражают более вероятные результаты, в то время как более короткие области отражают широкий диапазон чисел, чтобы зафиксировать процент распределения.

На рисунке 1 показано нормальное распределение, которое является симметричным. Ее также называют кривой нормального распределения, и ее очень часто можно увидеть в данных. Большинство данных в нормальном распределении сгруппированы вокруг среднего значения. Чем дальше значение от среднего, тем меньше вероятность его возникновения. Для идеального нормального распределения:

Среднее и медиана будут одним и тем же значением, представленным пиком кривой
Около двух третей распределения будут достаточно близки к среднему, в пределах 1 стандартного отклонения
95% будут находиться в пределах 2 стандартных отклонений

Для тех, кто занимается шестью сигмами, вы можете заметить, что примерно 1 из 1 миллиона наблюдений отличается от среднего более чем на 6 стандартных отклонений (или 6 сигм).

Рисунок 1: Кривая нормального распределения, показывающая распределение наблюдений вокруг среднего значения. Приблизительно 95% популяции находится в пределах 2 стандартных отклонений от среднего, а 5% — дальше

Среднее — это лишь один из параметров, определяющих нормальное распределение. Другой параметр — стандартное отклонение. Большее стандартное отклонение приводит к более широкой кривой, но величина распределения в пределах каждого диапазона стандартного отклонения одинакова.

Рис. 2. Низкое стандартное отклонение, означающее, что данные сгруппированы вокруг медианы. Это приводит к кривой с более высоким пиком (кривая синего колокола). Высокое стандартное отклонение означает, что данные разбросаны от среднего значения, что приводит к кривой с более плоским и широким пиком (оранжевая кривая) хвоста или распределения дальше от среднего по обе стороны от распределения. Данные о платежах для организации имеют тенденцию к искажению вправо. Причина в том, что многие работники могут получать заработную плату в нижней или левой части распределения, ни один из них не получает ноль или меньше нуля, а некоторые избранные имеют довольно высокую заработную плату.

Как показано на рисунках 3 и 4, симметричные распределения будут иметь одно и то же среднее значение и медиану, в то время как асимметричное распределение будет иметь среднее значение, отличное от медианы, основанной на асимметрии. Распределение с большим отрицательным перекосом будет иметь левый хвост, тогда как распределение с большим положительным перекосом будет иметь правый хвост.

Рис. 3. Симметричное распределение данных с одинаковыми средним значением и медианой

Рис. 4. Асимметричное распределение со средним значением, отличным от медианы. В правостороннем распределении среднее значение будет выше медианы

В статистическом анализе (включая анализ справедливости в оплате труда) важно работать с данными, близкими к нормальным после учета наших факторов в оплате, а асимметрия может исказить результаты. Чтобы скорректировать это, логарифмическая функция обычно используется для преобразования асимметричного распределения в симметричное распределение.

3. Статистические выводы и проверка гипотез

Вернуться к началу

Основной целью статистики является использование чисел для получения осмысленных выводов и понимания данных. Два типичных метода для этого основаны на доверительных/прогнозных интервалах и проверке гипотез.

Доверительный интервал

Доверительный интервал — это диапазон уверенности в том, что параметр (часто среднее) будет находиться между парой значений вокруг среднего. Это также часто называют погрешностью. Например, основываясь на данных о продажах автомобилей, мы можем сказать, что на 95 % уверены, что средние продажи с течением времени составят от 480 000 до 600 000[2]. Предел вероятности может быть установлен на любое число, наиболее распространенным из которых является уровень достоверности 95% или 99%.

Интервал предсказания

Интервал предсказания — это диапазон уверенности в том, что предсказание попадет между парой предсказанных значений вокруг среднего. Например, мы можем сказать, что на 95 % уверены, что продажи в следующем году составят от 360 000 до 740 000. Предел вероятности может быть установлен на любое число, наиболее распространенным из которых является уровень предсказания 95% или 99%.

Рисунок 5: Верхний и нижний интервалы прогнозирования с доверительным интервалом

Сравнение доверительных интервалов и интервалов прогнозирования
Доверительный интервал используется при попытке найти параметр генеральной совокупности, например среднее значение. Интервал прогнозирования используется при попытке предсказать, где будет лежать одно наблюдение. Следовательно, интервал прогнозирования будет шире, чем доверительный интервал. И доверительные интервалы, и интервалы прогнозирования становятся меньше, если имеется больше наблюдений и более низкое стандартное отклонение среди наблюдений.

Проверка гипотезы

Это набор статистических тестов для определения того, подтверждают ли данные данный вывод. Например, мы можем проверить, равны ли долгосрочные средние продажи нашего автосалона 450 000 или больше 600 000.

В исследовании равенства в оплате труда проверяемая гипотеза состоит в том, что оплата труда мужчин и женщин, представителей меньшинств и не меньшинств в фирме одинакова после учета соответствующих факторов. Важно отметить, что мы никогда не сможем сделать вывод о том, существует ли разрыв. Вместо этого тест основывается на вероятности обнаружения данных, которые мы получили, если нет разрыва. Затем модель многомерной регрессии проверяет, есть ли веские доказательства, опровергающие эту гипотезу. Возможны два варианта, как показано на рис. 6.

Рисунок 6: Два возможных исхода проверенной гипотезы

Эти исходы связаны с доверительными интервалами. Если разрыв, равный нулю, выходит за пределы доверительного интервала, мы находим доказательство сильным.

Статистическая значимость

Статистическая значимость — это способ заявить, что мы находим убедительные доказательства результата в статистическом анализе. Это не означает, что число вызывает беспокойство, а отсутствие статистической значимости не означает, что это не так. Вместо этого он просто указывает, можем ли мы сделать вывод, что различия не вызваны случайным шумом в данных.

Уровень достоверности

Уровень достоверности показывает, насколько мы должны быть уверены, чтобы сделать вывод о том, что результат является статистически значимым. В анализе равенства в оплате труда и других социальных науках мы обычно используем вероятность 5%. Это означает, что 1 из 20 исследований приведет к «ложноположительному» заключению об отсутствии справедливости, когда популяция сбалансирована. Более высокий уровень достоверности также увеличивает ширину доверительного интервала и, следовательно, вероятность «ложноотрицательного результата», когда мы не можем определить существующую проблему.[3]

P-значение

P-значение показывает, насколько вероятно, что мы найдем значение, по крайней мере столь же экстремальное, как и в нашем анализе, при условии, что нулевая гипотеза верна . Например, в случае с компанией ABC мы можем увидеть 1% вероятность того, что средний объем продаж превысит 600 000. Из этого можно сделать вывод, что средний объем продаж ниже 600 000, и это статистически значимо.

В исследовании равенства в оплате труда, если мы видим разрыв в 2% между заработной платой мужчин и женщин, а p-значение равно 10%, это означает, что результат не является статистически значимым (хотя мы не можем сказать, что — это не пробел).

Разница средних значений (Т-критерий)

Т-критерий предназначен для определения того, является ли среднее значение двух групп одинаковым. Важно отметить, что этот тест не включает никаких элементов управления. Но его можно использовать, чтобы увидеть, одинаковы ли продажи автомобилей в июле и августе за последние 30 лет или одинаковы ли средние доходы мужчин и женщин в определенной группе.

4. Регрессионный анализ и переменные

Вернуться к началу

Когда мы рассматриваем равенство в оплате труда, мы рассматриваем не просто одну переменную. Скорее, мы хотим посмотреть на взаимосвязь между несколькими переменными, в частности, оплатой труда и такими переменными, как роль, опыт и производительность. Регрессионный анализ является основным методом проверки справедливости в оплате труда. Эти инструменты, основанные на изучении взаимосвязи переменных, позволяют нам моделировать оплату труда сотрудников, используя ряд прогнозных переменных.

Корреляция

Корреляция — это статистическая мера, устанавливающая величину и направление связи между двумя переменными. Например, переменными могут быть скидки и продажи автомобилей, где чем больше скидка, тем выше продажи автомобилей. Корреляция измеряется коэффициентом корреляции (r) и может находиться в диапазоне от +1,0 до -1,0.

Если коэффициент корреляции равен 0, это указывает на отсутствие связи между переменными (одна переменная может оставаться постоянной, а другая увеличивается или уменьшается).

Если коэффициент корреляции имеет отрицательное значение (ниже 0), это указывает на отрицательную связь между переменными.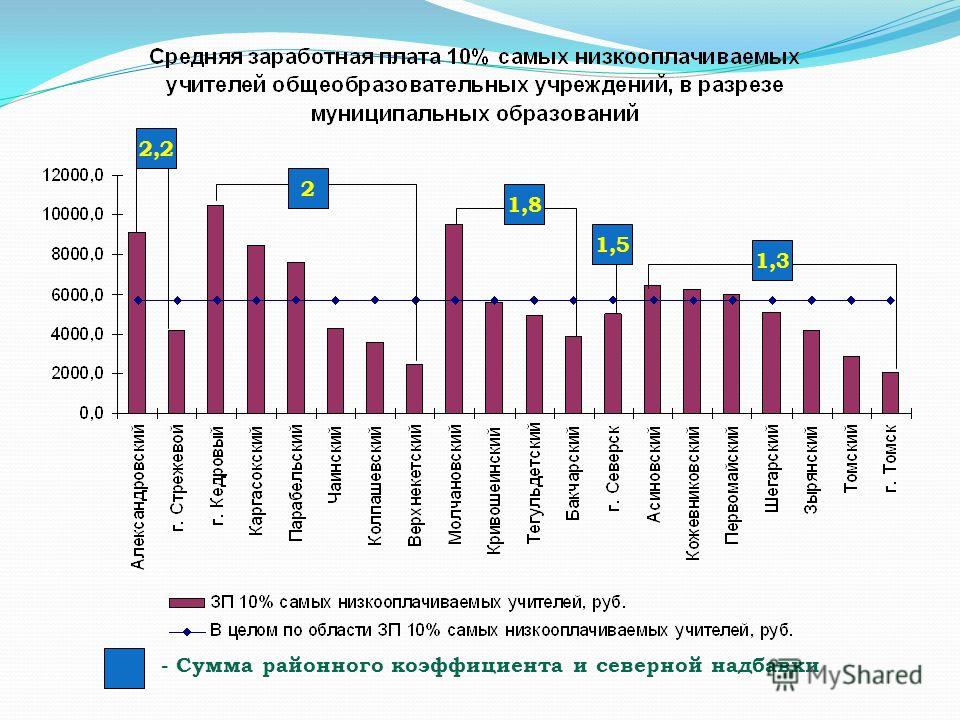 Это означает, что переменные движутся в противоположных направлениях (то есть, когда одна увеличивается, другая уменьшается, или когда одна уменьшается, другая увеличивается).

Если коэффициент корреляции имеет положительное значение (выше 0), это указывает на положительную связь между переменными. Это означает, что обе переменные движутся в тандеме (то есть, когда одна переменная уменьшается, другая также уменьшается, или когда одна переменная увеличивается, другая также увеличивается). В исследовании справедливости в оплате труда большинство переменных, используемых для объяснения заработной платы, как правило, положительно коррелируют с оплатой труда. На рисунках 7 и 8 показано, как могут выглядеть данные для двух переменных с положительной корреляцией.

Рисунок 7: Диаграмма рассеяния для двух переменных, которые не так сильно коррелированы

Рисунок 8: Диаграмма рассеяния для двух переменных, которые сильно коррелированы исследование представляет собой регрессионный анализ. Регрессионный анализ — это класс статистических инструментов, который позволяет аналитикам анализировать одну переменную, контролируя различия между другими переменными.

Регрессионный анализ позволяет контролировать различные независимые переменные, чтобы предсказать результат зависимой переменной.

В исследовании справедливости в оплате труда регрессионный анализ можно рассматривать как механизм, посредством которого одновременно учитываются все движущиеся части, влияющие на оплату труда (роль, производительность, местонахождение и т. д.). Цель состоит в том, чтобы количественно определить, могут ли оставшиеся различия в оплате труда быть связаны с несоответствующими факторами, такими как пол и этническая принадлежность .

Регрессия находит наиболее подходящую линию по набору данных. Цель состоит в том, чтобы объяснить зависимую переменную (оплата в случае исследования справедливости в оплате труда) в контексте независимых переменных , таких как роль, опыт, производительность и местоположение, которые, как считается, влияют на заработную плату. Регрессия показывает, как меняется заработная плата в ответ на изменения последней. При разработке модели надежда состоит в том, что она не найдет доказательств того, что такие факторы, как пол или этническая принадлежность, объясняют разницу в оплате труда.

Давайте попробуем понять эту концепцию на простом примере с самой платой. Предположим, что небольшая компания, в которой работает всего 20 сотрудников, имеет только один независимый фактор — срок пребывания в должности, влияющий на заработную плату. Формула на рисунке 9иллюстрирует, как срок пребывания в должности используется в регрессионном анализе для объяснения оплаты труда.

Рисунок 9: Срок владения как независимая переменная в регрессионном анализе

Вышеупомянутое уравнение можно визуализировать на графике регрессии. На рис. 10 каждый сотрудник представлен синей точкой на осях стажа работы (горизонтальная) и заработной платы (вертикальная). Простая регрессия по этим переменным приводит к тому, что через диаграмму рассеяния проводится прямая линия, которая наиболее точно пересекает точки и минимизирует выбросы. Эта линия показана оранжевым цветом и иллюстрирует прогнозируемый уровень оплаты для каждого срока пребывания в должности.

Рисунок 10: Диаграмма рассеяния и линия регрессии для одномерной регрессии

Если мы вспомним наши уроки алгебры в старшей школе, эта линия представляет собой классическую y=mx + b или концепцию пересечения наклона.

Конкретное уравнение для показанной выше линии: y=39,83+9,56x , где:[4]

это оплата, предсказанная регрессией
39,83 — точка пересечения или начальная точка линии, где она пересекает вертикальную ось (в тысячах)
это годы пребывания в должности
9,56 — наклон линии или сумма оплаты (в тысячах), связанная с каждым дополнительным годом пребывания в должности. Это известно как коэффициент , потому что он умножается на значение x

Это простой пример только с одной независимой переменной. На самом деле может быть несколько факторов (независимых переменных), влияющих на заработную плату. В таких случаях уравнение регрессии можно расширить, используя коэффициенты соответствующих переменных.

Зависимая переменная

В регрессионном анализе основная переменная, которую мы пытаемся предсказать или понять, называется зависимой переменной. Это также называется целевой переменной или переменной Y на основе графического соглашения о размещении их на вертикальной оси. Часто проще всего помнить, что это переменная, которая зависит от других. Типичными зависимыми переменными могут быть цена акций, завтрашняя погода или результаты тестов учащегося.

Для исследования справедливости в оплате труда зависимой переменной будет та, которая используется для понимания и прогнозирования заработной платы работника.

Независимые или независимые переменные

В регрессионном анализе факторы, которые, как мы подозреваем, могут оказывать влияние на зависимую переменную, называются независимыми переменными. Их также часто называют объяснительными, предикторными или X-переменными.

Согласно исследованию справедливости в оплате труда, это факторы, которые, по нашему мнению, потенциально могут повлиять на оплату труда. Неполный список может включать должностные обязанности, предыдущий опыт работы, срок пребывания в компании, срок пребывания на текущей должности, корректировку местоположения/стоимости жизни, рейтинг производительности, образование, требования к командировкам и обязанности руководителя.

В регрессионном анализе независимые переменные могут быть как числовыми, так и категориальными:

Числовые переменные — действительные числа (например, возраст сотрудника или стаж работы в компании)
Категориальные переменные могут иметь два или более возможных значения, обычно качественных (таких как должностная роль, название должности или рейтинги производительности)

Фиктивная или индикаторная переменная — это числовая переменная, которая представляет категориальную информацию. Они двоичные, то есть могут иметь два возможных значения. В нашем примере с автомобилем мы могли бы посмотреть на ежедневные продажи и использовать дождь в качестве фиктивной переменной, чтобы проверить, менее ли вероятно, что люди будут покупать автомобили в плохую погоду. В нашем анализе равенства в оплате труда фиктивная переменная для пола может иметь значение либо 0, либо 1 (представляющее мужчину и женщину). Следовательно, для переменной, представляющей пол, каждая запись в данных будет иметь значение либо 0, либо 1.[5]

Логарифмическое (логарифмическое) преобразование

В реальных наборах данных распределение не всегда поддается регрессии. Он часто искажен, что может привести к неверным результатам регрессии. Например, представьте, что мы регрессируем размер мозга животных по массе их тела. В этом случае ошибка слона может быть намного больше, чем всего тела мыши.

Если в распределении есть проблема, из-за которой более крупные наблюдения кажутся еще более разбросанными,[6] мы можем нормализовать распределение, чтобы результаты стали более достоверными.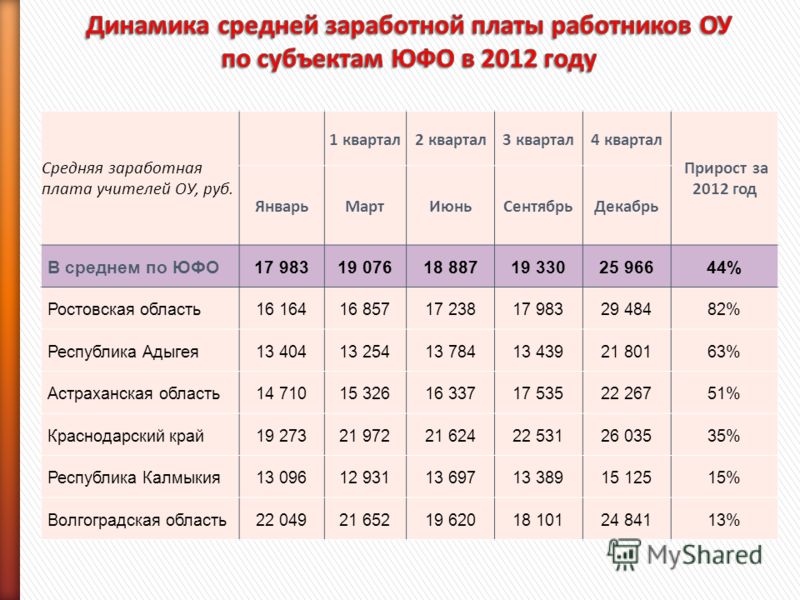 Логарифмическое преобразование помогает уменьшить шум и асимметрию данных, чтобы сделать результаты регрессии статистически достоверными

Вы, возможно, помните из школы стандартную логарифмическую (по основанию 10) функцию:

В нашем анализе мы делаем то же самое, но используем число Эйлера, приблизительно 2,718, обычно известное как «e»,[7] в качестве основания некоторым удобным статистическим свойствам. Исходя из результата, вы можете считать разницу в результатах журнала такой же отражающей, как и процентное изменение x.

В исследовании равенства в оплате труда ожидается, что зависимая переменная (оплата) будет в значительной степени следовать асимметричному распределению, при котором никто не зарабатывает менее 0 долларов, большой набор низкооплачиваемых сотрудников и несколько очень высокооплачиваемых сотрудников находятся в верхней части распределения. . Использование логарифмического преобразования оплаты помогает устранить эту асимметрию и обеспечить регрессию, которая соответствует базовым предположениям о данных (которые выходят далеко за рамки этого учебника).

5. Выходные данные регрессии и выбросы

Вернуться к началу

После проектирования и запуска окончательной регрессии наша модель дает нам разные выходные данные. Здесь мы сосредоточимся на некоторых ключевых из них, которые появятся в нашем анализе.

Коэффициенты

Это влияние каждой из наших переменных x в регрессии. В нашем предыдущем уравнении y=39,83+9,56x, предположим, что y — это заработная плата, а x — срок пребывания в должности. Таким образом, коэффициент стажа в этом уравнении равен 9..56 . Это означает, что если срок пребывания в должности увеличится на 1 год, ожидаемое значение y (зарплаты) увеличится на 9,56.

В дополнение к опыту, исследование справедливости в оплате труда может иметь различные переменные, влияющие на оплату (например, местонахождение, образование, рейтинги производительности, надзорные обязанности, уровень управления и т. д.). Регрессионная модель создает коэффициенты для каждой из этих независимых переменных, чтобы помочь определить их влияние на оплату труда.

Пока мы обсуждаем коэффициенты и переменные в регрессии, было бы полезно обсудить индикаторные или фиктивные[8] переменные. Эффект фиктивной переменной, где x равен 0 или 1, представляет собой две разные линии регрессии, одну для контрольной группы и одну для тестовой группы, разделенные коэффициентом. В анализе равенства в оплате труда критическая проверка гипотезы заключается в том, что влияние манекена пола равно нулю. Если мы обнаружим доказательства того, что это не так, и гендерный показатель действительно влияет на регрессию, то это покажет разницу в оплате труда в зависимости от пола (см. рис. 11).

Рисунок 11: Две разные линии регрессии для мужчин и женщин. Основываясь на приведенном выше уравнении регрессии, ожидается, что женщина с пятилетним стажем заработает 81 292 доллара, а мужчина с таким же опытом получит дополнительные 23 826 долларов, или в общей сложности 105 118 долларов. модель линейной регрессии, значение R-квадрата является мерой «хорошего соответствия» модели. Это определяет, насколько хорошо модель соответствует данным, или, другими словами, насколько различия объясняются нашими x-переменными.

Значение квадрата R может находиться в диапазоне от 0% до 100%. Более низкий R-квадрат представляет собой высокую дисперсию между подобранными значениями и точками данных и наоборот. Визуальные графики ниже иллюстрируют более высокий и более низкий R-квадрат.

Рисунок 12: R-квадрат для модели 86%. Большинство точек данных сгруппированы вокруг линии регрессии. Модель может объяснить 86% дисперсии и, следовательно, лучше подходит

Рисунок 13: R-квадрат для модели 53%. Большое количество точек данных разбросано далеко от линии регрессии, что означает, что модель может объяснить только 53% дисперсии

Низкое значение R-квадрата является проблемой?
Не обязательно! Это зависит от различных факторов, таких как тип анализа, размер выборки, количество и вид независимых переменных. Исследования погодных условий, как правило, имеют более низкий R-квадрат по сравнению с продажами автомобилей, потому что погоду предсказать труднее, чем продажи автомобилей. Точно так же, если в регрессионном исследовании есть ряд независимых переменных, влияние которых неясно или трудно предсказать, то ожидается, что модель будет иметь низкий R-квадрат.
Если мы используем большое количество независимых переменных в регрессионной модели для небольшого размера выборки, то R-квадрат может быть очень высоким. На самом деле, добавление дополнительных переменных только увеличит значение. Однако это может указывать на проблему подгонки модели, что не является идеальным.
Поэтому важно проверить p-значение оценок самих переменных. Если сами переменные статистически значимы, то модель, возможно, является хорошим предиктором зависимой переменной, независимо от значения R-квадрата.

Остаточный/ошибочный термин

Когда мы проводим регрессионный анализ, мы получаем линию наилучшего соответствия. Различные точки данных разбросаны по линии наилучшего соответствия. Остаток — это просто расстояние по вертикали между точкой данных и линией наилучшего соответствия. Другими словами, это разница между наблюдаемым значением и прогнозируемым значением.

На рис. 14 точки над линией наилучшего соответствия указывают на положительную невязку. Для этих точек данных предсказанное значение выше, чем наблюдаемое значение. Точки под линией указывают на отрицательный остаток. Для этих точек данных прогнозируемое значение ниже наблюдаемого значения.

Выброс

Регрессионный анализ также информирует нас о выбросах. Выбросы — это наблюдения, выходящие за пределы предсказанного диапазона регрессионной модели. Другими словами, это наблюдения, которые плохо вписываются в модель, например, с неожиданно высоким или низким значением. Статистически установлено, что выброс — это значение наблюдения, выходящее за пределы соответствующего интервала прогнозирования, или наблюдение с p-значением 0,05 или меньше.

В нашем контексте равенства в оплате труда регрессия генерирует прогнозируемое значение оплаты для каждого человека и соответствующий интервал прогнозирования. Люди, чья фактическая заработная плата выходит за пределы этого прогнозируемого диапазона, затем помечаются как выбросы. Это сотрудники, которых мы идентифицируем для дальнейшего рассмотрения или исправления. Поскольку p-значение отражает случайную изменчивость данных, мы ожидаем, что около 5% населения будут выбросами.

Рисунок 15: График кумулятивного распределения, где ось X показывает, насколько фактическая заработная плата отличается от ожидаемого уровня. Отрицательные выбросы — это нижние 5%, а положительные выбросы — верхние 5% распределения вероятностей. В связи с этим область слева от вертикальной средней (50%) разделительной линии показывает случаи, когда фактическая заработная плата падает ниже ожидаемой, а случаи справа включают фактическую заработную плату, превышающую ожидаемую заработную плату

Рисунок 16: Выброс №1 и выброс № 2, два сотрудника, чья зарплата выходит за пределы прогнозируемого интервала 9. 0%. Выброс № 2 оплачивается выше прогнозируемого диапазона, а выброс № 1 оплачивается ниже прогнозируемого диапазона

Заключение

В регрессионном анализе есть несколько других терминов и инструментов, которые могут возникнуть. Инструменты, которые будут использоваться, зависят от цели, задачи и глубины исследования. Поэтому не существует единой модели, отвечающей всем требованиям. Чаще всего модели необходимо настраивать, чтобы они могли помочь объяснить изменения и наблюдения в данных более надежным способом.

Мы надеемся, что эта статья оказалась вам полезной. Если у вас есть какие-либо вопросы по темам, которые мы здесь рассмотрели, или об исследованиях равенства в оплате труда в целом, мы будем рады получить от вас известие.

Вернуться к началу

[1] Читатели, более склонные к статистике, могут заметить, что правило 95% применяется к данным при нормальном распределении, в то время как 75% данных находятся в пределах 2 стандартных отклонений для всех распределений.

[2] Выбора пяти точек данных обычно недостаточно для расчета статистически приемлемого доверительного интервала. Обычно минимальный размер выборки составляет 30 человек. Причина этого не в статистическом колдовстве. Дело в том, что этот объем данных позволяет нам разумно сказать, что среднее значение нормально распределено, используя центральную предельную теорему.

[3] Много внимания уделяется правилу 95%. Мы склонны думать об этом как о разумном сомнении из судебного дела. Поскольку социальные науки содержат данные с большим количеством шума, мы готовы принять небольшие различия. Компромисс с большим количеством ложных срабатываний компенсируется более высокой вероятностью обнаружения проблем. В производственных приложениях этот допуск может значительно уменьшиться. Например, Lego утверждает, что менее чем в одном из тысячи наборов отсутствует необходимая деталь. Клиенты могут быть недовольны, если им досталась комплектация только 95% времени. При изготовлении космического челнока число отказов может составлять один случай на миллион.

[4] Вы можете заметить, что в обычно используемом «y=mx+b» член x находится в начале, тогда как в нашей регрессии порядок переворачивается. Простая причина заключается в том, что для множественной регрессии у нас есть несколько переменных x, и удобнее расположить их вместе в порядке

[5]. разбиты в анализах из-за меньшего количества сотрудников. Однако также можно использовать отдельную переменную индикатора для захвата нескольких групп.

[6] Статистический термин для этого — гетероскедастичность, где гетеро означает «другой», а скедастичность относится к ошибкам.

[7] Вы можете обращаться с e как с pi. Это математическое «магическое число», обладающее некоторыми замечательными статистическими свойствами. Однако число Эйлера (произносится как «майлер») страдает отсутствием шуток «пи/пи».

[8] «Манекен» относится к тому факту, что это индикатор, и не дает суждений об интеллекте. С учетом вышесказанного наша практика заключается в том, чтобы всегда присваивать мужчинам фиктивное значение.

Статистика и население

Дом
Конспект лекций
Журналы статистики
R Журналы
Наборы данных
Наборы задач

Наборы задач

Дом Конспект лекций Журналы статистики Журналы R Наборы данных Наборы задач

Статус
Р

Начнем с чтения данных

 . используйте https://grodri.github.io/datasets/wages, очистите
(Почасовая заработная плата в выписке CPS 1985 г.)

 > библиотека(убежище)
> заработная плата <- read_dta("https://grodri.github.io/datasets/wages.dta")
> имена (зарплата)
 [1] «образование» «юг» «женщина» «рабочий опыт» «член профсоюза»
 [6] "зарплата" "возраст" "этническая принадлежность" "род занятий" "отрасль"
[11] «женат»

[1] Работа с заработной платой

(a) Подберите линейную модель, чтобы исследовать, как почасовая заработная плата зависит от образование, опыт работы, членство в профсоюзе, регион, профессия и секс.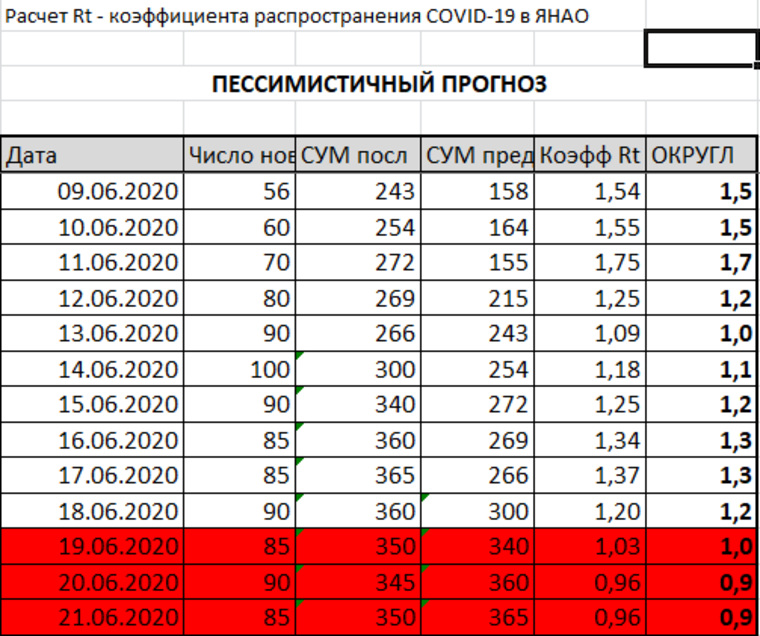 (Для простоты мы опускаем другие предикторы в этом набор задач.)

. регресс заработная плата educ workexp union юг i.оккупация женщина Источник │ SS df MS Количество наблюдений = 534 F 10, 523) = 24,39 Модель │ 4477.32498 10 447.732498 Вероятность > F = 0,0000 Остаток │ 9599,37357 523 18,3544428 R-квадрат = 0,3181 ─────────────┼─────────────────────────────j -квадрат = 0,3050 Итого │ 14076,6985 533 26,4103162 СКО корня = 4,2842 ─диимобилил ───────────────────────────── заработная плата │ Коэффициент стд. ошибаться т П>|т| [95% конф. интервал] ─диимобилил ───────────────────────────── образование │ .6722878 .09

 6,79 0,000 .4777169 .8668586
      рабочийэкспр │ .0936955 .0165623 5,66 0,000 .0611587 .1262322
  член союза │ 1,517377 ,5083565 2,98 0,003 ,5187055 2,516049
        юг │ -.6885843 .4150423 -1,66 0,098 -1,503939 .1267705
              │
   занятие │
       Продажи │ -3,975443 ,9141984 -4,35 0,000 -5,771395 -2,179491
    Канцелярский │ -3,347118 . 7600163 -4,40 0,000 -4,840178 -1,854058
     Сервис │ -4,148184 .8053377 -5,15 0,000 -5,730278 -2,56609Профессиональные │ -1,267909 ,7270285 -1,74 0,082 -2,696164 ,1603461
       Другое │ -2,799024 ,756551 -3,70 0,000 -4,285276 -1,312772
              │
       самка │ -1,845267 .4152299 -4,44 0,000 -2,66099 -1,029544
        _cons │ 1,979516 1,710527 1,16 0,248 -1,380831 5,339863
─диимобилил ─────────────────────────────
. оценивает заработную плату в магазине

> m1 <- lm(зарплата ~ образование + опыт работы + член профсоюза + юг + профессия + женщина, + данные = заработная плата) > резюме (м1) Вызов: lm (формула = заработная плата ~ образование + опыт работы + член профсоюза + юг + профессия + женщина, данные = заработная плата) Остатки: Мин. 1 кв. Медиана 3 кв. Макс. -90,484 -2,786 -0,710 1,788 37,376 Коэффициенты: Оценка стд. Значение ошибки t Pr(>|t|) (Пересечение) -3,36151 1,46609 -2,293 0,02225 * образование 0,

0,08142 11,097 < 2e-16 *** рабочийэксп 0,10447 0,01685 6,200 1,14e-09 *** член профсоюза 1,44405 0,52270 2,763 0,00593 ** юг -0,78659 0,42699 -1,842 0,06601 .

занятие -0,06183 0,12459 -0,496 0,61990 самка -2,20661 0,39750 -5,551 4,50э-08 *** --- Сигн. коды: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 '' 1 Остаточная стандартная ошибка: 4,416 на 527 степенях свободы. Множественный R-квадрат: 0,2698, скорректированный R-квадрат: 0,2615 F-статистика: 32,45 на 6 и 527 DF, p-значение: <2,2e-16

(b) Опишите чистый эффект образования, опыта работы и профсоюза членство по заработной плате.

Почасовая оплата на 67 центов выше за год обучения для рабочих с теми же наблюдаемыми значениями других переменных. Опыт работы есть связано с увеличением почасовой оплаты труда на 9 центов в год. опыт, а все остальное то же самое. Члены профсоюза зарабатывают 1,52 доллара. больше в час, чем не члены профсоюза с теми же характеристиками

Работающие женщины зарабатывают в среднем 1,85 долл. США в час меньше чем мужчины с одинаковым образованием, опытом работы, членством в профсоюзе, регионом места жительства и занятий. Гипотеза о том, что женщины делают то же, что и сопоставимые мужчины отклоняются со статистикой t -4,4 (P-значение от нуля до трех знаков после запятой.)

(d) Рассчитайте и нанесите на график невязки складного ножа в зависимости от подогнанной ценности. На что указывает сюжет? Любые выбросы?

 . предскажи джек, рсту
. предсказать fv
(предполагается вариант xb; подобранные значения)
. скаттер джек фв
. экспорт графика ps2fig1.png, ширина(500) заменить
файл ps2fig1.png, сохраненный в формате PNG

 > библиотека (dplyr)
> библиотека (ggplot2)
> заработная плата <- мутировать (заработная плата, n = row_number (), jack = rstudent (m1), fv = приспособленный (m1),
+ lev = hatvalues(m1)) # добавлено кредитное плечо для последующего использования
> ggplot(зарплата, aes(fv, jack)) + geom_point()
> ggsave("ps2fig1r.png", ширина=500/72, высота=400/72, dpi=72)

На графике показана типичная модель мегафона, которая указывает гетероскедастичность; дисперсия остатков явно больше при более высокая прогнозируемая почасовая оплата. Мы также видим очень четкий выброс; а работник, чья заработная плата более чем на 8 стандартных отклонений выше ожидал.

(e) Вычислите надежные стандартные ошибки и прокомментируйте, разрыв по-прежнему значителен. (Пользователи R должны обязательно использовать «HC1» метод.)

. тихо регрессировать заработную плату образование профсоюз юг i.occupation женщина, vce(надежный) . оценки хранят надежные . расчетная таблица заработной платы робастная, се ─────────────┬────────────────────────── Переменная │ стабильная заработная плата ─────────────┼────────────────────────── образование │ .67228777 .67228777 │ 0,09

5 .10155895
     рабочийэкспр │ .09369546 .09369546
             │ .01656226 .01934914
 член профсоюза │ 1,5173771 1,5173771
             │ .50835653 .5257942
       юг │ -.68858431 -.68858431
             │ .41504228 .38976722
             │
  занятие │
      Продажи │ -3,9754434 -3,9754434
             │ .91419841 1.1030045
   Канцелярский │ -3,3471181 -3,3471181
             │ . 76001633 1.0812816
    Сервис │ -4.1481844 -4.1481844
             │ .80533767 1.1210233
Профессия~l │ -1,2679088 -1.2679088
             │ .72702849 1.1014587
      Другое │ -2,79 -2,79

             │ .75655098 1.0819253
             │
      женщина │ -1,8452669 -1,8452669
             │ .41522986 .44311694
       _cons │ 1,9795165 1,9795165
             │ 1,7105266 2,0648923
─────────────┴──────────────────────────
                            Легенда: б/с

 > библиотека (lmtest)
> библиотека (сэндвич)
> надежный <- coeftest(m1, vcov = vcovHC(m1, type = "HC1"))
> cbind(coeftest(m1)[1:3], робастный[2:3])
              Оценка стд. Значение ошибки t Станд. Значение ошибки t
(Перехват) -3,3615053 1,46609296 -2,2928323 1,74989163 -1,9209792
образование 0,95 0,08142273 11,0967729 0,09379948 9,6325641
workexp 0,1044667 0,01685018 6,1997403 0,01928569 5,4168003
член профсоюза 1,4440454 0,52269625 2,7626856 0,51594119 2,7988566
юг -0,7865931 0,42699097 -1,8421773 0,41387499 -1,72
занятие -0,0618297 0,12458542 -0,4962836 0,15128362 -0,4087006
женщина -2,2066130 0,39750111 -5,5512122 0,39970760 -5,5205679

Устойчивые стандартные ошибки несколько больше, чем на основе модели оценок, но гендерный разрыв по-прежнему значителен: т соотношение больше 4.

[2] Работа с логарифмом заработной платы

(a) Соответствуйте модели части 1.a, работая с натуральным логарифмом почасовая заработная плата.

. gen logwages = log(зарплата) . регресс logwages educ union юг i.occupation workexp женщина Источник │ SS df MS Количество наблюдений = 534 F 10, 523) = 27,97 Модель │ 51,7302552 10 5,17302552 Prob > F = 0,0000 Остаток │ 96,7165671 523 ,184926514 R-квадрат = 0,3485 ─────────────┼─────────────────────────────j -квадрат = 0,3360 Итого │ 148,446822 533 ,278511862 СКО корня = 0,43003 ─диимобилил ───────────────────────────── заработная плата │ Коэффициент стд. ошибаться т П>|т| [95% конф. интервал] ─диимобилил ───────────────────────────── образование │ .0694744 .0099415 6,99 0,000 .0499442 .08

член союза │ .205853 .0510267 4,03 0,000 .1056106 .3060955 юг │ -.1060423 .0416602 -2,55 0,011 -.1878842 -.0242005 │ занятие │ Продажи │ -.3504642 .0917634 -3,82 0,000 -. 5307343 -.1701941 Канцелярский │ -.2176053 .0762872 -2,85 0,005 -.3674724 -.0677382 Сервис │ -.4042984 .0808364 -5.00 0.000 -.5631024 -.2454945 Профессиональный │ -.0432898 .0729761 -0,59 0,553 -.186652 .1000724 Другое │ -.2047711 .0759394 -2,70 0,007 -.3539548 -.0555873 │ рабочийвыраж │ .0105903 .0016624 6,37 0,000 .0073244 .0138562 женский │ -.2080284 .041679 -4.99 0.000 -.2899072 -.1261495 _cons │ 1,251034 ,1716955 7,29 0,000 ,9137368 1,588332 ─диимобилил ─────────────────────────────

 > m2 <- lm(log(зарплата) ~ образование + опыт работы + член профсоюза + юг + профессия + женщина,
+ данные = заработная плата)
> резюме (м2)
Вызов:
lm(formula = log(зарплата) ~ образование + опыт работы + член профсоюза +
    юг + профессия + женщина, данные = заработная плата)
Остатки:
    Мин. 1 кв. Медиана 3 кв. Макс.
-2,1249-0,2853 -0,0056 0,2953 1,9778
Коэффициенты:
             Оценка стд. Значение ошибки t Pr(>|t|)
(Перехват) 0,705778 0,147282 4,792 2,15e-06 ***
образование 0,094708 0,008180 11,579 < 2e-16 ***
рабочийэкспр 0,011611 0,001693 6,859 1,95e-11 ***
член союза 0,194787 0,052509 3,710 0,00023 ***
юг -0,111674 0,042895 -2,603 0,00949 **
занятие 0,003969 0,012516 0,317 0,75129
самка -0,229623 0,039932 -5,750 1,51э-08 ***
---
Сигн.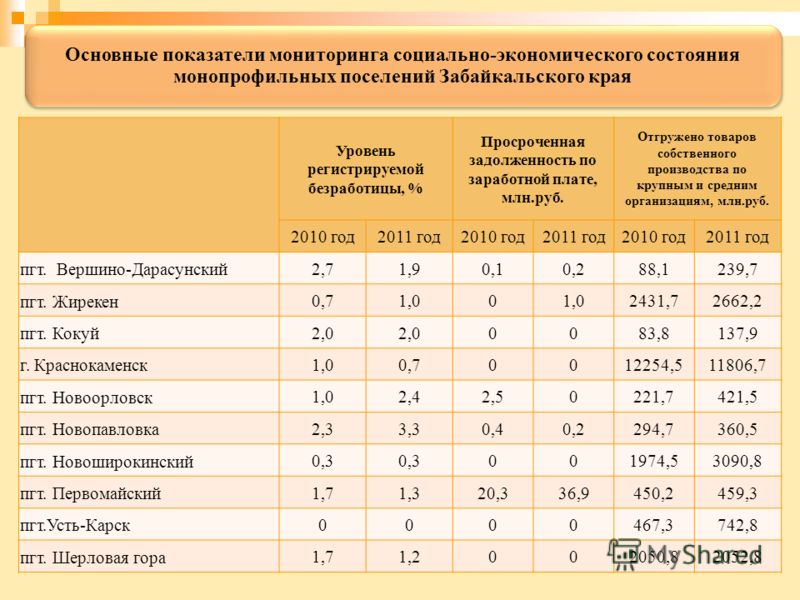  коды: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 '' 1
Остаточная стандартная ошибка: 0,4437 при 527 степенях свободы.
Множественный R-квадрат: 0,3012, скорректированный R-квадрат: 0,2932
F-статистика: 37,86 на 6 и 527 DF, p-значение: <2,2e-16

(b) Опишите коэффициенты образования, опыта работы и профсоюза членство с точки зрения влияния этих переменных на заработную плату (не на журнал заработной платы).

 . mata b = st_matrix ("e (b)")
. мата b[1..3] \ exp(b[1..3])
                  1 2 3
    ┌─────────────────────────────────────────┐
  1 │ .0694743579 .2058530126 -.1060423388 │
  2 │ 1,071944574 1,228572606 .8993865683 │
    └──────────────────────────────────────────

 > vars = c("образование","рабочий опыт","член профсоюза")
> ехр(коэффициент(м2)[варс]) - 1
  образование workexp unionmember
 0,09933768 0,01167847 0,21505242

Мы оцениваем отдачу от образования как повышение заработной платы на 7,2% в год образование, при прочих равных условиях. Рабочие с большим опытом сделать в среднем примерно на один процент больше за год опыта, корректируя для всего остального. Члены профсоюза зарабатывают в среднем на 23% больше в час чем не входящие в профсоюз работники с теми же наблюдаемыми характеристиками. Первый два коэффициента достаточно малы, чтобы интерпретировать их непосредственно как проценты, но аппроксимация менее точна для коэффициента объединения. Вы можете увидеть все коэффициенты в возведенной в степень форме, используя рег, eform(e(b)) .

Коэффициент -0,208 соответствует относительному эффекту 0,812, что указывает на то, что работающие женщины зарабатывают в среднем 81 цент на доллар, по сравнению с мужчинами с таким же образованием, опытом работы, профсоюзом членство, регион проживания и род занятий. Т-тест -4,99 на 523 д.ф. весьма значителен, что указывает на то, что разница слишком большой, чтобы быть из-за случайности.

(d) Проверить, одинакова ли отдача от трудового стажа для самцы и самки.

Добавляем взаимодействие между индикатором для женщин и работой опыт и проверка его значимости

 . gen workXfem = workexp * женщина
. регресс logwages educ workexp union юг i.occupation женский workXfem
      Источник │ SS df MS Количество наблюдений = 534
F 11, 522) = 26,11
       Модель │ 52,6813635 11 4,78921486 Prob > F = 0,0000
    Остаток │ 95,7654588 522 ,183458733 R-квадрат = 0,3549
─────────────┼─────────────────────────────j -квадрат = 0,3413
       Итого │ 148,446822 533 ,278511862 СКО корня = 0,42832
─диимобилил ─────────────────────────────
     заработная плата │ Коэффициент стд. ошибаться т П>|т| [95% конф. интервал]
─диимобилил ─────────────────────────────
    образование │ .0714044 .0099382 7,18 0,000 .0518806 .0909282
      рабочийэкспр │ .0140507 .0022475 6,25 0,000 .0096353 .018466
  член союза │ .1964052 .0509929 3,85 0,000 .0962287 .2965817
        юг │ -.110057 .041532 -2,65 0,008 -.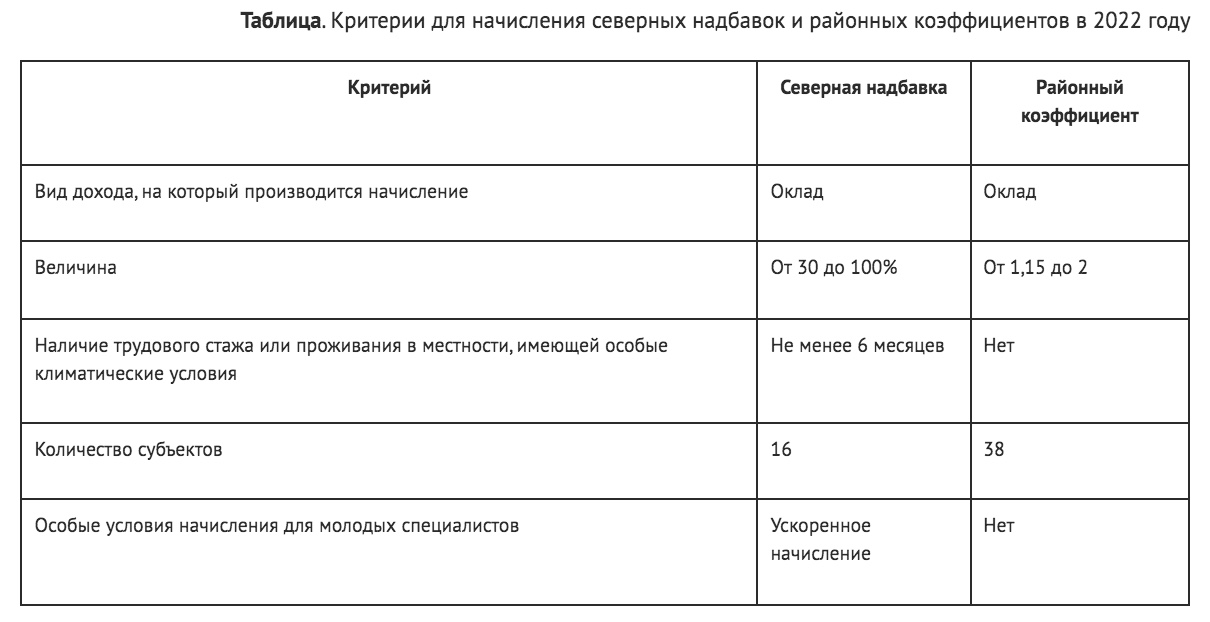 1916474 -.0284666
              │
   занятие │
       Продажи │ -.344788 .0914325 -3,77 0,000 -.5244089 -.1651672
    Канцелярские │ -.2024009 .0762767 -2,65 0,008 -.352248 -.0525538
     Сервис │ -.3819969 .0811085 -4,71 0,000 -.5413362 -.2226577
Профессиональный │ -.0367114 .0727433 -0.50 0.614 -.1796169 .1061942
       Другое │ -.1890991 .07595 -2,49 0,013 -.3383042 -.039894
              │
       женский │ -.0858201 .0678538 -1,26 0,207 -.21912 .0474799
     workXfem │ -.0069357 .0030461 -2.28 0.023 -.0129198 -.0009516
        _cons │ 1,158463 ,1757792 6,59 0,000 ,8131414 1,503784
─диимобилил ─────────────────────────────

 > m3 <- update(m2, ~ . + workexp:female)
> резюме (м3)
Вызов:
lm(formula = log(зарплата) ~ образование + опыт работы + член профсоюза +
    юг + профессия + женщина + workexp:женщина, данные = заработная плата)
Остатки:
     Мин. 1 кв. Медиана 3 кв. Макс.
-2,15124 -0,28771 -0,00452 0,29728 1,
Коэффициенты:
                Оценка стд. Значение ошибки t Pr(>|t|)
(Перехват) 0,616172 0,149806 4,113 4,53e-05 ***
образование 0,095662 0,008134 11,760 < 2e-16 ***
рабочийэкспр 0,015884 0,002273 6,989 8. 39е-12***
член союза 0,183934 0,052317 3,516 0,000476 ***
юг -0,116439 0,042654 -2,730 0,006549 **
занятие 0,005904 0,012455 0,474 0,635698
женщина -0,073762 0,068422 -1,078 0,281508
workexp:женщина -0,008700 0,003111 -2,796 0,005362 **
---
Сигн. коды: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 '' 1
Остаточная стандартная ошибка: 0,4408 при 526 степенях свободы.
Множественный R-квадрат: 0,3114, скорректированный R-квадрат: 0,3023
F-статистика: 33,99 на 7 и 526 DF, значение p: < 2,2e-16

Член взаимодействия является значимым при обычных пяти процентах уровень. Результаты показывают, что почасовая заработная плата выше на 1,4% в год. опыт для мужчин, но только на 0,7% выше в год опыта для самки с такими же характеристиками. Другими словами, предполагаемая отдача от опыта у женщин вдвое меньше, чем у мужчин. (я продолжал работать опыт не центрирован, потому что 0 опыт работы имеет смысл и интересный. Если бы я сосредоточил его, я бы получил гендерный разрыв в средний опыт как «основной» эффект жен. .)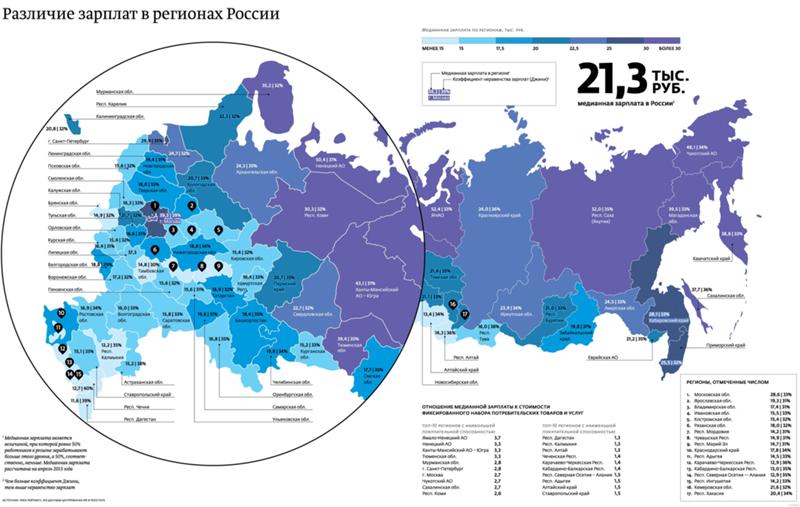

(e) Как результат части (d) влияет на выводы части (с)? У нас все еще есть гендерный разрыв?

 . сумма трудозатрат
    Переменная │ Набл. Среднее ст. разв. Мин Макс
─диимобилил ─────────────────────
     трудэксп │ 534 17,8221 12,37971 0 55
. di exp(_b[женщина]) - 1, exp(_b[женщина] + r(среднее) * _b[workXfem]) - 1
-.08224064 -.18895215

 > mwe <- среднее(зарплата$workexp)
> b <- коэффициент (м3)
> c(exp(b["женщина"]), exp(b["женщина"] + mwe * b["workexp:женщина"])) - 1
    женский пол
-0,0711070 -0,2045184

Да, этот результат влияет на наши выводы. В части (c) мы оценили средний гендерный разрыв по всему диапазону опыта. На самом деле разрыв меньше среди новых работников, но увеличивается со временем. Среди новых работающие женщины зарабатывают на 8% меньше, чем сопоставимые мужчины, но разрыв увеличивается на 0,7 процентных пункта в год, поэтому при среднем стаже работы 17,8 лет она стала 19%.

[3] Диагностика регрессии

(a) Рассчитайте и нанесите на график невязки складного ножа в зависимости от подобранных значений для окончательной модели с использованием логарифмической заработной платы. Что нам говорит сюжет? Любой выбросы?

 . предсказать ljack, рсту
. предсказать лф
(предполагается вариант xb; подобранные значения)
. скаттер лджек lfv
. экспорт графика ps2fig2.png, ширина(500) заменить
файл ps2fig2.png, сохраненный в формате PNG

 > заработная плата <- мутировать(заработная плата, ljack = rстудент(m3), lfv = приспособленный(m3))
> ggplot(зарплата, aes(lfv, ljack)) + geom_point()
> ggsave("ps2fig2r.png", ширина=500/72, высота=400/72, dpi=72)

График значительно улучшился, хотя все еще есть намек на снижение дисперсия при очень низкой заработной плате. Выброс, который мы заметили раньше, переместился в немного, но теперь у нас есть рабочий, чья относительная заработная плата составляет почти шесть стандартные отклонения ниже прогнозируемых.

(b) Постройте быстрый график Q-Q, чтобы проверить нормальность остатков. Как график выглядит? (Формальный тест не требуется.)

Чтобы использовать ggplot , вам нужно вычислить квантили «вручную», как показано в логах R. Мы сделаем это простым способом с qqnorm() .

 . qnorm ljack
. экспорт графика ps2fig3.png, ширина(500) заменить
файл ps2fig3.png, сохраненный в формате PNG

 > png("ps2fig3r.png", ширина = 500, высота = 400, единицы = "px")
> qqnorm(зарплата $ljack)
> dev.off()
пдф
  2

Мы видим, что, за исключением двух только что отмеченных выбросов, наблюдения не далеки от нормы. Эти двое, однако, настолько далеки, что почти любой тест отверг бы предположение о нормальных остатках. (Вы можете попробовать swilk или sktest как проверка нормальности.)

(c) Рассчитайте рычаги. Есть ли у нас какие-либо наблюдения с высоким использовать? Определите наблюдение с самым высоким рычагом. Не могли бы вы скажите, почему это имеет потенциальное влияние?

 . предсказать лев, лев
. ген н = _ н
. уровень разброса n
. экспорт графика ps2fig4.png, ширина(500) заменить
файл ps2fig4.png, сохраненный в формате PNG

 > ggplot(зарплата, aes(n,lev)) + geom_point()
> ggsave("ps2fig4r. png", ширина=500/72, высота=400/72, dpi=72)

Мы видим три наблюдения со сравнительно большими рычагами, но ни один из них не является достаточно большим, чтобы вызывать беспокойство. Перечислим три самые большие:

 . list n заработная плата educ workexp female lev if lev > 0,06
     ┌ackindyacsideabults ─────┐
     │ n заработная плата, образование, труд, женский уровень │
     ├ackindyacsideabults ─────┤
 63. │ 63 7 3 55 0 .0621579│
347. │ 347 6 4 54 0 .0672973 │
351. │ 351 3,75 2 16 0 ,0718959 │
     └acредить acмобили ─────┘
. сумма образования
    Переменная │ Набл. Среднее ст. разв. Мин Макс
─диимобилил ─────────────────────
   образование │ 534 13,01873 2,615373 2 18

 > заработная плата |> фильтр(уровень > .06) |>
+ select(n, зарплата, образование, workexp, женщина, лев)
# Таблица: 0 × 6
# … с 6 переменными: n , зарплата , образование , workexp ,
# женщина , лев 
> среднее (зарплата $ образование)
[1] 13.01873

Наивысший леверидж — мужчина с двухлетним стажем работы. образование. У него есть рычаги воздействия, потому что его образование значительно ниже среднее, и получает дополнительные рычаги, потому что это сочетается с сравнительно небольшой стаж работы. (Вы можете найти поучительный сюжет образование по сравнению с опытом работы.)

(d) Рассчитайте расстояния Кука. Есть ли у нас какие-либо наблюдения, которые выделяться? Как вы думаете, что произойдет с гендерным разрывом, если мы переоборудуем модель, опускающая наблюдение с наибольшим фактическим влиянием? (Не нужно делать подгонку.)

 . предсказывать повар, готовить
. разбрасывать повар жен.
. экспорт графика ps2fig5.png, ширина(500) заменить
файл ps2fig5.png, сохраненный в формате PNG

 > заработная плата <- мутировать(заработная плата, повар = повара.расстояние(м3))
> ggplot(зарплата, aes(n, повар)) + geom_point()
> ggsave("ps2fig5r.png", ширина=500/72, высота=400/72, dpi=72)

Нет близко к единице. Многие превышают эмпирическое правило 4/(n-p) . Но есть два, которые намного крупнее всех остальных:

. gen pwages = exp(lfv)
. список n заработная плата pwages educ occup workexp женщина повар если повар > .04
     ┌ackindyacside ─────────┬────────┐
171. │ n │ заработная плата │ заработная плата │ образование~n │ профессия │ workexp │ женщина │
     │ 171 │ 44,5 │ 7,999821 │ 14 │ Управление │ 1 │ 1 │
     ├ackindyacside ─────────┴────────┤
     │ готовить │
     │ .0437665 │
     └ackindyacsideabults ──────────────────┘
     ┌ackindyacside ─────────┬────────┐
200. │ n │ заработная плата │ заработная плата │ образование~n │ профессия │ workexp │ женщина │
     │ 200 │ 1 │ 10,51214 │ 12 │ Менеджмент │ 24 │ 0 │
     ├ackindyacside ─────────┴────────┤
     │ готовить │
     │ .0634495 │
     └ackindyacsideabults ──────────────────┘

 > заработная плата <- мутировать(заработная плата, pwages = exp(lfv))
> зарплата |> фильтр(повар > 0.04) |>
+ выберите(n, заработная плата, pwages, образование, опыт работы, женщина, повар)
# Таблетка: 2 × 7
      n заработная плата pwages образование workexp женский повар
        
1 171 44,5 6,65 14 1 1 0,0459
2 200 1 8,60 12 24 0 0,0472

Крупнейший из них – менеджер-мужчина с 23-летним стажем, который составляет только 1 доллар в час, когда мы ожидаем 10,51 доллара. Если бы мы опустили это наблюдения, мы ожидаем, что гендерный разрыв увеличится. Второй — женщина-менеджер почти без опыта, зарабатывающая 44,5 доллара. Исключение она также увеличила бы гендерный разрыв. Однако они имели бы противоположное влияние на срок взаимодействия. Интересно, что ни один из Случаи с высоким кредитным плечом в конечном итоге оказали фактическое влияние на соответствие.

(e) Нам нужно было преобразовать данные? Был ли натуральный логарифм хорошая трансформация? Изучите эти вопросы в рамках концепции Бокс-Кокса. построение логарифмической вероятности профиля для параметров в диапазоне (-2,2) и формальное тестирование идентичности и преобразований журнала.

Оказывается boxcox не позволяет факторные переменные, так что мы вычисляем фиктивные профессии и срок взаимодействия сами. В приведенном ниже коде используются метки значений для именования оккупационные манекены.

 . для значений кошка = 2/6 {
  2. местное имя: метка (род занятий) `кот'
  3.  gen occ_`name' = род занятий == `cat'
  4. }

Теперь мы следуем процедуре, изложенной в Stata logs для построения логарифмического правдоподобия профиля.

 . ген лямбда = .
(создано 534 пропущенных значения)
. ген ll = .
(создано 534 пропущенных значения)
. местный xvars educ workexp union южный occ_* женский workXfem
. местный я = 0
. для значений p = -2(0,5)2 {
  2. тихо упаковать `xvars', iterate(0) from(`p',copy)
  3. локальный i = `i' + 1
  4. незаметно заменить lambda = `p' на `i'
  5. незаметно заменить ll = e(ll) в `i'
  6. }
. график twoway mspline ll лямбда в 1/9, bands(9) ytitle(Профиль log-lik)
. экспорт графика ps2fig6.png, ширина(500) заменить
файл ps2fig6.png, сохраненный в формате PNG

Мы используем библиотеку MASS , как показано на Журналы R

 > библиотека (МАССА)
> m4 <- update(m1, ~ . + workexp:female)
> png ("ps2fig6r.png", ширина = 500, высота = 400, единица измерения = "px")
> bc <- boxcox(m4)
> dev.off()
пдф
  2

Вы можете запустить boxcox команда, чтобы увидеть тесты в сводной таблице в конце. я побегу тихо, чтобы получить оценку и логарифмическое правдоподобие, а затем вычислить тест из вывода у меня уже есть:

 . спокойно Boxcox зарплаты `xvars'
. di _b[theta:_cons], e(ll)
-.01530901 -1398.4514
. спокойно gen chisq = -2*(ll - e(ll))
. перечислить лямбда все chisq, если inlist(лямбда, -1, 0, 1)
     ┌───────────────────────────────┐
     │ лямбда-чиск │
     ├───────────────────────────────┤
  3. │ -1 -1543,741 290,5793 │
  5. │ 0 -1398,482 .0612271 │
  7. │ 1 -1526,194 255,4846 │
     └───────────────────────────────┘

Очевидно максимум недалеко от лога трансформация, но boxcox не говорит нам, где именно. Мы можем найти его, используя optim()

 > f <- function(lam) -boxcox(m4, lambda=lam, plotit=FALSE)$y
> opt <- оптимизировать (f, интервал = c (-1,1))
> выбрать
$минимум
[1] -0,0211955
$цель
[1] 1235.376

Так что наилучшее преобразование -0,015 с логарифмом 1217.997. Эта информация в основном используется для тестирования выбранных преобразования.

Районный коэффициент к заработной плате: Районный коэффициент и северная надбавка 2022: как рассчитать, пример расчета